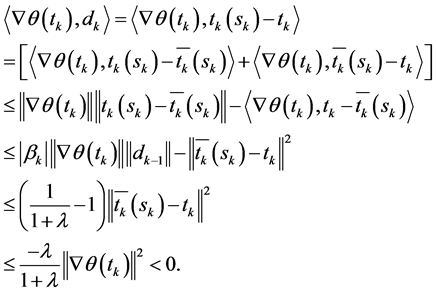Received 2 May 2016; accepted 10 June 2016; published 13 June 2016

ABSTRACT

In this paper, a class of the stochastic generalized linear complementarity problems with finitely many elements is proposed for the first time. Based on the Fischer-Burmeister function, a new conjugate gradient projection method is given for solving the stochastic generalized linear complementarity problems. The global convergence of the conjugate gradient projection method is proved and the related numerical results are also reported.

Keywords:

Stochastic Generalized Linear Complementarity Problems, Fischer-Burmeister Function, Conjugate Gradient Projection Method, Global Convergence

1. Introduction

Suppose 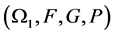is a probability space with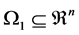; P is a known probability distribution. The stochastic generalized linear complementarity problems (denoted by SGLCP) is to find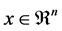, such that

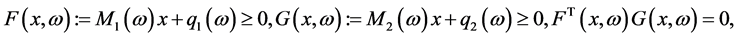(1)

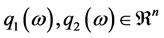where and for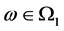, are random matrices and vectors. When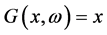, stochastic generalized linear complementarity problems reduce to the classic Stochastic Linear Complementarity Problems (SLCP), which has been studied in [1] - [7] . Generally, they usually apply the Expected Value (EV) method and Expected Residual Minimization (ERM) method to solve this kind of problem.

If 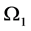only contains a single realization, then (1) reduces to the following standard Generalized Linear Complementarity Problem (GLCP), which is to find a vector 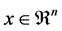such that

,

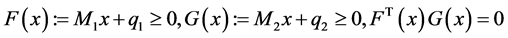where 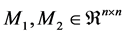and.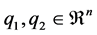

In this paper, we consider the following generalized stochastic linear complementarity problems. Denote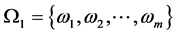, to find an 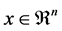such that

(2)

Let, where, ,. Then (2) is equivalent to (3) and (4)

(3)

(4)

In the following of this paper, we consider to give a new conjugate gradient projection method for solving (2). The method is based on a suitable reformulation. Base on the Fischer-Burmeister function, x is a solution of (3), where

.

Define

.

Then solving (3) is equivalent to find a global solution of the minimization problem

.

So, (3) and (4) can be rewritten as

, (5)

where

,

is slack variable with,.

Let, where and. Then we know that has equations with variables.

Let and define a merit function of (5) by

.

If (2) has a solution, then solving (5) is equivalent to find a global solution of the following minimization problem

(6)

where.

2. Preliminaries

In this section, we give some Lemmas, which are taken from [8] - [10] .

Lemma 1. Let P be the projection onto Ω, let for given and, then

1), for all.

2) P is a non-expansive operator, that is, for all.

3).

Lemma 2. Let be the projected gradient of θ at.

1).

2) The mapping is lower semicontinuous on Ω, that is, if, then

.

3) The point is a stationary point of problem (6) Û.

3. The Conjugate Gradient Projection Method and Its Convergence Analysis

In this section, we give a new conjugate gradient projection method and give some discussions about this method.

Given an iterate, we let,

, (7)

where. Inspired by the literature [8] - [11] , we take

, (8)

with.

And is defined by

. (9)

Method 1. Conjugate Gradient Projection Method (CGPM)

Step 0: Let, , , , , set.

Step 1: Compute, such that

,

.

Set.

Step 2: If, stop,.

Step 3: Let, and go to Step 1.

In order to prove the global convergence of the Method 1, we give the following assumptions.

Assumptions 1

1) has a lower bound on the level set, where t₁ is initial point.

2) is continuously differentiable on the L₀, and its gradient is Lipschitz continuous, that is, there exists a positive constant L such that

.

Lemma 3. If t_k is not the stability point of (6), , then search direction d_k generated by (9) descent

direction, which is.

Proof. From (7), Lemma 1, and (8), we have

Lemma 4. [11] Suppose that Assumptions 1 holds. Let continuously differentiable and lower bound on the Ω, is uniformly continuous on the Ω and is bounded, then generated by Method 1 are satisfied

,.

Theorem 1. Let continuously differentiable and lower bound on the Ω, is uniformly conti-

nuous on the Ω, is a sequence generated by Method 1, then, and any accumulation

point of is a stationary point of (6).

Proof. By Lemma 2, we have, , , satisfy

, (10)

for, by Lemma 1, we know that, and we have

, so,

. (11)

Let, , from (11), we have

.

By the above formula, (8) and Lemma 1, we get

Taking limit on both sides and by Lemma 4, we know that

. (12)

Because

(13)

and Lemma 4, we have

. (14)

By (12), (13), (14) and is uniformly continuous on the Ω, we get

.

By (10), we know that

. (15)

Let, where, by Lemma 2 and (15), we have

.

From Lemma 2 3), we get any accumulation point of is a stationary point of (6).

4. Numerical Results

In this section, we give the numerical results of the conjugate gradient projection method for the following given test problems, which are all given for the first time. We present different initial point t₀, which indicates that Method 1 is global convergence.

Throughout the computational experiments, according to Method 1 for determining the parameters, we set the parameters as

.

The stopping criterion for the method is or.

In the table of the test results, t₀ denotes initial point, denotes the solution, val denotes the final value of

, Itr denotes the number of iteration.

Example 1. Considering SGLCP with

, ,

, ,

and,.

The test results are listed in “Table 1” using different initial points.

Example 2. Considering SGLCP with

, ,

, ,

and,.

The test results are listed in “Table 1” using different initial points.

5. Conclusion

In this paper, we present a new conjugate gradient projection method for solving stochastic generalized linear complementarity problems. The global convergence of the method is analyzed and numerical results show that Method 1 is effective. In future work, large-scale stochastic generalized linear complementarity problems need to be studied and developed.

Acknowledgements

This work is supported by National Natural Science Foundation of China (No. 11101231, 11401331), Natural Science Foundation of Shandong (No. ZR2015AQ013) and Key Issues of Statistical Research of Shandong Province (KT15173).

Cite this paper

Zhimin Liu,Shouqiang Du,Ruiying Wang, (2016) A New Conjugate Gradient Projection Method for Solving Stochastic Generalized Linear Complementarity Problems. Journal of Applied Mathematics and Physics,04,1024-1031. doi: 10.4236/jamp.2016.46107

References