Journal of Applied Mathematics and Physics
Vol.04 No.09(2016), Article ID:70896,17 pages
10.4236/jamp.2016.49180
Impulse Spatial-Temporal Domains in Semiconductor Laser with Feedback
Igor B. Krasnyuk
Institute for Physics and Engineering Named after A. A. Galkin, Donetsk, Ukraine

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 19, 2016; Accepted: September 24, 2016; Published: September 27, 2016
ABSTRACT
An initial value boundary problem for system of diffusion equations with delay arguments and dynamic nonlinear boundary conditions is considered. The problem describes evolution of the carrier density and the radiation density in the semiconductor laser or laser diodes with “memory” and with feedback. It is shown that the boundary problem can be reduced to a system of difference equations with continuous time. For large times, solutions of these equations tend to piecewise constant asymptotic periodic wave functions which represent chain of shock waves with finite or infinite points of discontinuities on a period. Applications to the optical systems with linear media and nonlinear surface optical properties with feedback have been done. The results are compared with the experiment.
Keywords:
Initial Boundary Value Problem, Semiconductor Laser, Solutions of Relaxation Type, A Set of Attractive Fixed Points, A Set of Attractive Fixed Points, Asymptotic Periodic Distributions

1. Introduction
We consider semiconductor lasers or laser diodes [1] - [11] . The laser is inverted carrier density system. There exist carrier generation and recombination that is when electrons interact with hole, they recombine. The energy released can be produced by thermal recombination or optical photon recombination which is used in semiconductor lasers. An electronic oscillator is an electronic circuit that produces a periodic signal. Oscillators convert direct current to an alternative current signal. We use the feedback oscillator which can increase amplitudes of signal.
We consider “surface” oscillator which can be described mathematically by the functional or dynamic boundary conditions with feedback of the following form:
 (1)
(1)
where  is the corresponding amplitude of input signal, and
is the corresponding amplitude of input signal, and 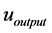 is the am- plitude of output signal. Here,
is the am- plitude of output signal. Here, 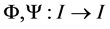 are given nonlinear functions which model the transform of signal with help of laser diodes or bipolar junction transistor. Next, we can use semiconductor laser with nonlinear layer which produces the process of recombination of electrons and holes, and the density of radiation. For surface inverse system, this process of recombination can be given by nonlinear function with feedback. Such nonlinearity may be produced by heating.
are given nonlinear functions which model the transform of signal with help of laser diodes or bipolar junction transistor. Next, we can use semiconductor laser with nonlinear layer which produces the process of recombination of electrons and holes, and the density of radiation. For surface inverse system, this process of recombination can be given by nonlinear function with feedback. Such nonlinearity may be produced by heating.
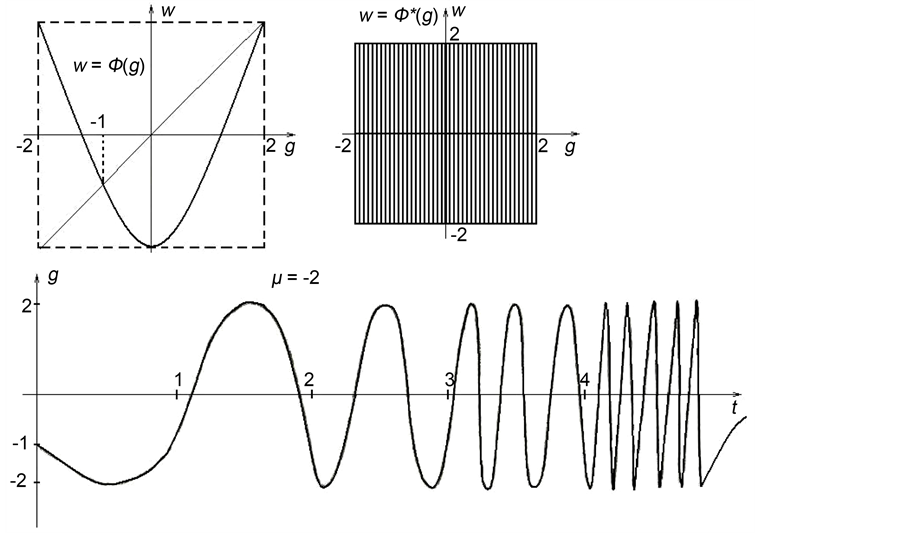
There are different physical mechanisms which can convert an optical signal. We consider an “deal” resonator when conversion of signal with feedback takes place at walls which confines the resonator. It will be shown that nonlinear surface optical properties of material produce in the volume of ideal resonator asymptotic periodic piecewise constant wave structures with finite or infinite number of “jumps” of am- plitude. Such distributions of electron, holes and radiation together represent shock waves. If a number of “jumps” are finite on a period, we have dealt asymptotic dis- tributions of relaxation type as time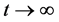 . If this number is infinite countable or infinite uncountable on a period, we get limit shock waves of pre-turbulent and turbulent type, correspondingly. Such periodic shock waves take place in
. If this number is infinite countable or infinite uncountable on a period, we get limit shock waves of pre-turbulent and turbulent type, correspondingly. Such periodic shock waves take place in 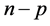 -type semiconductor lasers.
-type semiconductor lasers.
A corresponding mathematical model can be described for semiconductors with “memory” by a system of diffusion equations with delay arguments with dynamic nonlinear boundary conditions. To be more precise, the structure of shock waves depends not only on surface structure of material, which is described mathematically by the boundary conditions, but also from the initial data of the boundary problem that is from initial distribution of electrons, holes and density of radiation in the semi- conductor laser.
In last years, in physics studied the nonlinear interaction of light which can mimic the physics at so called an event horizon. As shown in [6] , this analogue arises when a weak probe wave is unable to pass through an intense soliton, despite propagating at a different velocity. These dynamics arise as a soliton-induced refractive index barrier. In all papers this barrier characterizes the volume optic properties of linear boundary conditions. In this paper, we consider the opposite problem when the optical medium is ideal or linear, but boundaries of the medium have the nonlinear optic properties, and describe, for example, the all-optical transistor [5] . It may be also a case when a bright soliton is passing through the soliton. In this case, the intensity of light depends on the refractive index. Thus, the soliton creates a moving refractive index’s perturbations which passage through the another soliton [1] [8] . This interaction between such surface solitons plays the main role of distributions of the light in the linear medium with nonlinear surface interaction. Thus for the ideal medium the main
role plays the surface nonlinear refractive index. In ( [5] , Figure 1) has been mimicked two spectral modes of solitons when the mode-locked laser diode generate picosecond solitons. This generation will be described as a functional boundary conditions with feadback generated these solitons. As noted in [1] , “intense pulse of light may be used to create an effective flowing medium which mimics certain properties of black hole physics”. Of course, analogues models can be realized in very different physical systems.
In this paper, an initial value boundary problem (IVBP) of system of two linear wave equations with nonlinear boundary conditions has been considered. Solutions of this problem describes the propagation of density of optical radiation (on a given frequency) and electron carriers in one-dimensional in the ideal semiconductor rod with optical defects at the ends. For example, the corresponding mathematical model describes the wave distributions of the density of radiation of photons and electron density in an ideal semiconductor. The semiconductor is confined by two flat walls which emit or absorb light. The probability of absorption or emission of photons depend on the surface density of the radiation and the surface density of electrons in a nonlinear manner. Diffusion in semiconductors is one-dimensional and one is directed orthogonal to the flat walls. Thus, the initial boundary value problem for the two linear wave type equations with nonlinear boundary conditions will be considered. This problem models different optical phenomena as white and black solitons, propagation of light in resonator with feedback connection between beams at walls and so on.
In this paper, we study the structure of attractor of the IVBP. The IVBP admits a
Figure 1. Solutions of turbulent type with the limit cantor set of points of discontinuities on a period. Phase portrait for simplest solutions of relaxation type (white and black solitons).
reduction to a differential-difference equations (DDE). We restrict ourselves to the case when the corresponding DDE are completely integrable. Indeed, among the differential- functional equations [12]
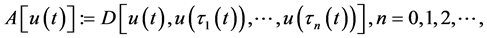 (2)
(2)
where A is a differential operator, 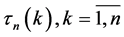 are delay arguments, there are a class of equations which admit decomposition on the finite product of differential and functional operators. Such equations are called equations with splitting operators [12] . The study of such equations reduces to a serial study of differential and functional equations. To this class belong to the so-called completely integrable equations [12] such that
are delay arguments, there are a class of equations which admit decomposition on the finite product of differential and functional operators. Such equations are called equations with splitting operators [12] . The study of such equations reduces to a serial study of differential and functional equations. To this class belong to the so-called completely integrable equations [12] such that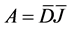 , where
, where  is a differential operator and
is a differential operator and 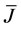 is a functional op- erator. For example, the equation
is a functional op- erator. For example, the equation
 (3)
(3)
is a completely integrable. Here, 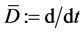 and
and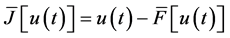 , where
, where  is some primitive of the function f. By integrating this equation can be reduced to one-parameter family of difference equations (DE) with continuous time:
is some primitive of the function f. By integrating this equation can be reduced to one-parameter family of difference equations (DE) with continuous time:
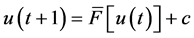 (4)
(4)
where c is some integrating constant. In general, the completely integrable equation
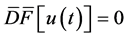 (5)
(5)
can be reduced to the family of functional non-autonomous equations
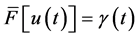
where 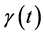
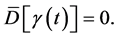
We consider distributions 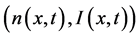
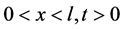

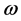
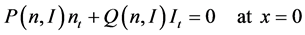
where 


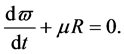
Since all the integrating factor described by the formula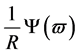

smooth function, there is a function F such that
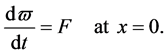
Let’s consider at the initial boundary value problem

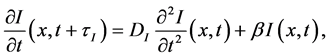
with the boundary conditions
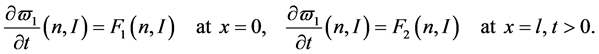
and the initial conditions
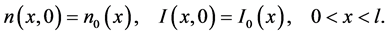
Here, 
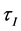

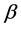
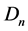

Thus, we consider asymptotic behavior of solutions for this of linear uncoupled equations with nonlinear dynamic boundary conditions. We define conditions on parameters, boundary functions and the initial conditions where there are asymptotic periodic piecewise constant solutions with finite or infinite points of discontinuities on a period. The paper is organized as follows.
2. Formulation of Problem
Consider a uniform rod such that the axis (Oz-axis) extends monochromatic radiation, characterized by the frequency 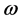

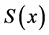

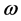
So we write the Burger law
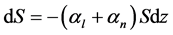
where 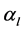
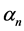
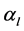
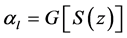
The corresponding model equation for densities of electrons and radiation is:
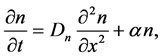

where 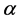
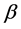


where 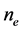


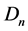
Let 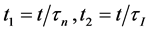
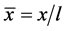


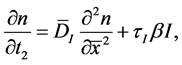
where
Now, instead of diffusion Equation (19) and Equation (20), we consider the diffusion equations with delay arguments:
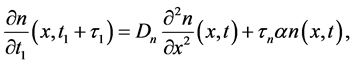
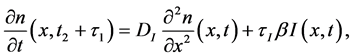
where 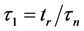
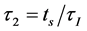
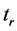
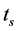
These equations describes distributions of the number of electrons and radiation in semiconductor. We assume that the number of electrons and holes is constant. The rise times 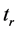
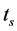

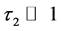
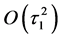
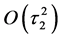
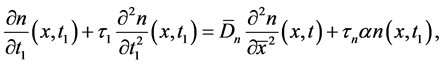
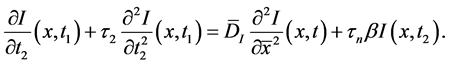
Since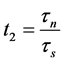
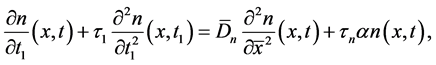
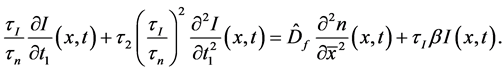
Bellow index in 
Note that the rise time can be determined by the formula
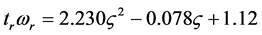
in the quadratic approximation, and by the formula
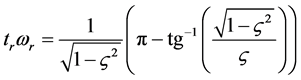
in the common case. Here, 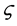
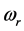
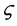
Note that the rise time 
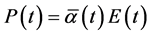
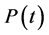
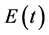
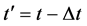
Let us consider for Equation (25) the dynamic boundary conditions

and the Neumann boundary conditions
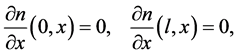
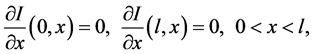
and the initial conditions
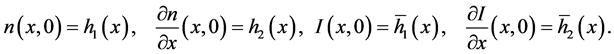
Let the solutions are
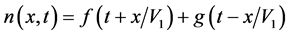

where 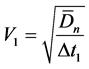
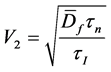
the equations
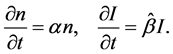
From (33), (33) it follows that Equations (35) can be written as
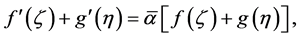
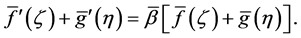
Without loss of generality, we assume that
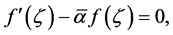
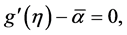
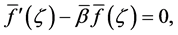

From the Neumann boundary conditions it follows that

where

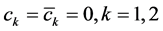
Now from (38) it follows that

Integrating this equation from 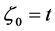
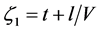
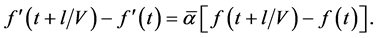
Next, integrating the equation
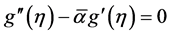
from 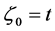
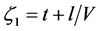

From (44), (46) it follows that
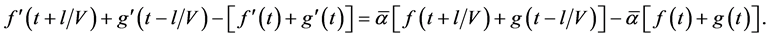
Then from the dynamic boundary conditions it follows that

From (42) it follows that Equation (48) can be written as
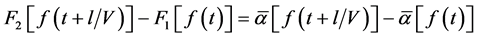
where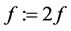
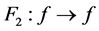

Let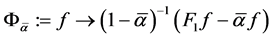
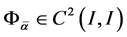
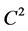

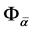
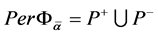
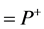
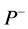

where 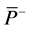

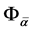

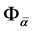

Let 
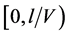
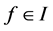




3. Example 1
Let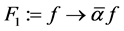
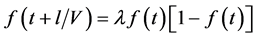
where

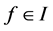
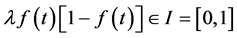

If

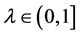
then 
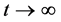

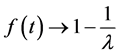



4. Reduction to Difference Equations
From the boundary conditions
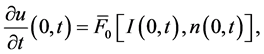
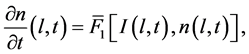
and the representation of solution in the form


it follows that
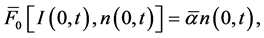
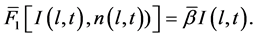
From the boundary conditions
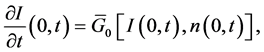
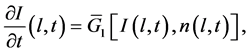
it follows that
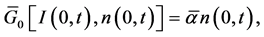

From the Neumann boundary conditions
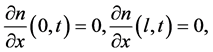
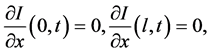
it follows that
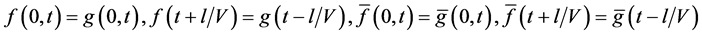
for a special choice of the initial conditions at the points

Then functional Equations (57), (58) and (61), (62) can be written as:
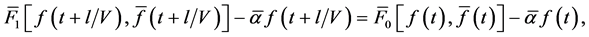
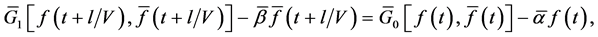
where 
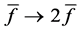
Let us assume that 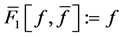

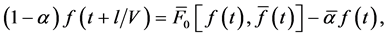
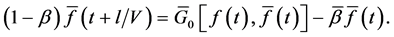
We got the system of difference equations with continuous time. This system
produce a map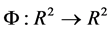

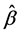

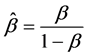
We assume that there is a bounded open subset 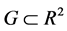
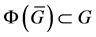
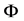
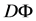
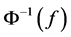
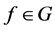
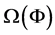
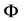

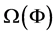
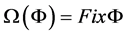






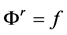
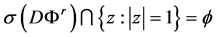
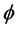
We will consider continuous solutions 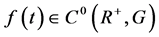
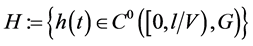
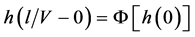

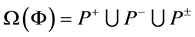
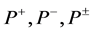
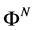

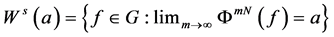
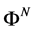
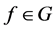
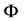
Then

where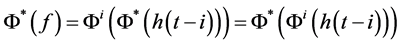

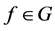

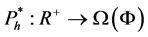
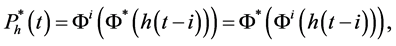
where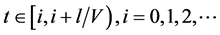
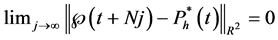
for each fixed point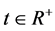
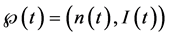
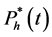
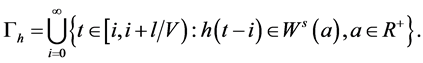
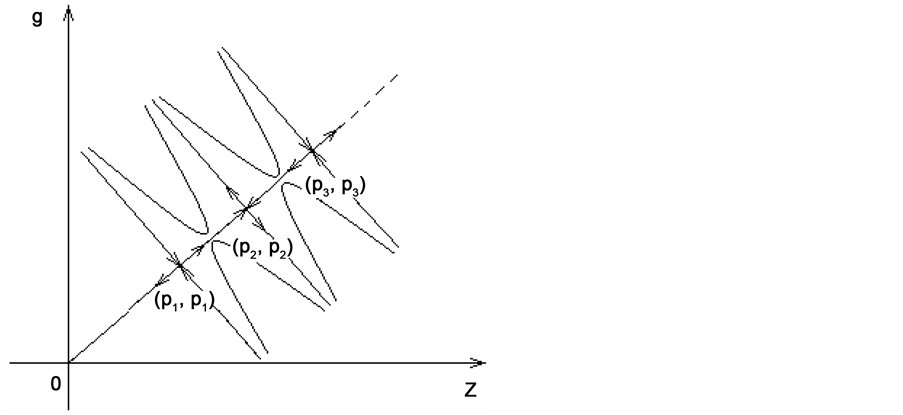
5. Example 2
Consider the system
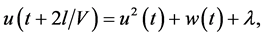
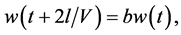
where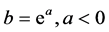

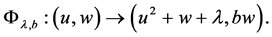
The set of non-wandering points of the map 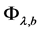

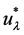

Let us define the initial curve
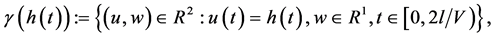
where the vector-function 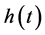
If 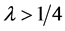


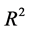

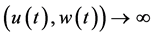





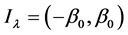
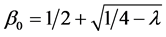
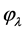
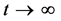
The solutions are bounded if and only if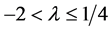
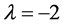
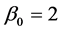

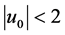
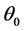
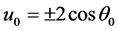
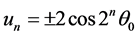
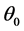
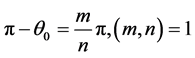

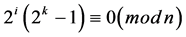
There is a set 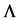
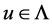
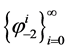
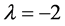
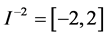

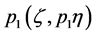
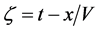
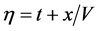

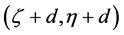



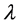
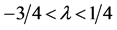
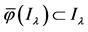
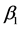


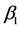
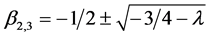
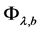
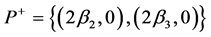
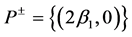
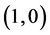


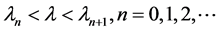
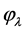
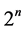
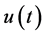
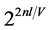
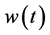
6. Physical Dynamic Boundary Conditions
Let us consider the following model [2] :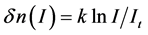
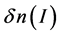
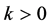
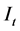
Figure 2. Phase portrait for simplest solutions of relaxation type (white and black solitons). 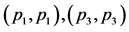
study propagation of a spatially incoherent, quasi-monochromatic and linearly po- larized light beam in a linear photopic lattice with a non-instantaneous surface non- linearity. The electron field fluctuates on time scale much shorter than the response time of the nonlinearity [4] . The state of the system can be described by a function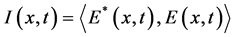

Now we show how can be postulated nonlinear boundary conditions. For plane waves the density is defined as
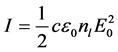
where c is velocity of light, 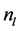

Indeed, as noted in [10] : “the nonlinear effects in optical fiber occur either due to intensity dependence of refractive index of the medium or due to inelastic-scattering phenomenon”. There are various types of nonlinear effects based on self-phase modu- lation, cross-phase modulations and four-wave mixing. We consider the effect when the refractive index is the nonlinear function of the optical intensity. The power dependence describes the Kerr-effect [10] . Origin of nonlinearity is the unharmonic motion of electrons under the action of the polarization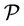
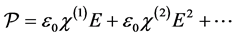
where 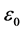
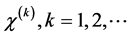
We assume that there is the surface polarization at a walls which confine the laser fiber. Then defects and color centers at the walls produce the second order gene- ralization. We confined itself by the study only the quadratic boundary conditions which describes wave type distributions of relaxation, pre-turbulent and turbulent type. Then the surface refractive index is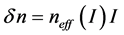
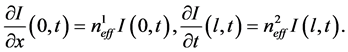
In similar form, we can consider more common boundary conditions. Then from (80) it follows that 
sider also the values 
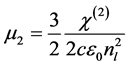
From the formula 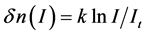
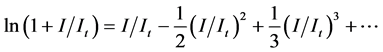
for 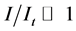
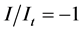
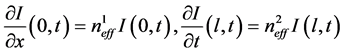
if

7. Applications to Semiconductor Lasers
In semiconductor lasers, the intersection field matter is realized through the carrier density n which satisfies to the equation [3] :
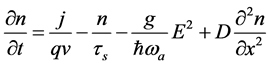
where
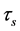
We assume that device is placed at a point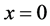
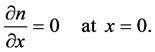
Next, we assume that the media of semiconductor laser is ideal that is light propagates throw the media without changing of amplitude along lines

We assume that

where 
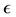
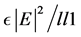
Next, we consider, additionally, the boundary conditions
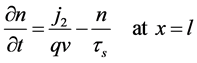
that is 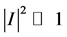
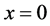
On the other hand, from the theory of the injection locking it follows that
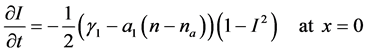
where 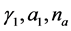
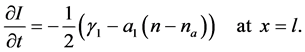
Thus we get the dynamic boundary conditions. Applying the method of reduction corresponding initial value boundary problem to a system of difference equations, we obtain that the problem has solutions of relaxation, pre-turbulent and turbulent type for a special case of the coefficients 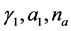
8. Comparison with Experiment
In [9] has beeb discusses the dynamics of modulation surface directed instability and periodic waves in the coupled linear equations which describes light propagation in dispersed Kerr media. New spatial-temporal periodic solutions are found for these equations. As noted in [9] : there is “the fundamental link which exists between the phenomenon of polarization instability and the so-called black and white vector solitons”. From this point of view, the asymptotic periodic spatial-temporal periodic solutions obtained in our paper are not the solitons, because solitons exists due to a balance between surface induced injection of radiation into optic media and volume radiation. Surface radiation with feedback can be modeled by laser diode. The balance can be achived only asymptotically as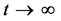
Spatial solitons were experimentally observed in 1997 by Mitchel and Segev (see, [11] ). Such solitons arise from incoherent white light and these solitons appears as a dynamic balance between the tendency for the beam to expend as a result of diffraction and the property of beam to contract as a result of self focusing. In [23] has been demonstrated solitons which can be obtained from both the spatially and temporally incoherent light. But, as noted in [11] , the corresponding theory can not explain spatial-temporal coherence properties and also properties of temporal spectral density of such solitons. We believe that the initial value boundary problem, which is con- sidered in the present paper, may be useful to describe formal properties of spatial- temporal solitons and their spectral properties.
9. Conclusion
In this paper, we analyze the dynamic of surface, and induce nonlinear instability in ideal optic volume producing light propagation, reflected from walls, which confines an ideal resonator. The problem is described by two linear difference equations with nonlinear dynamic boundary conditions for density of radiations and density of photons in the resonator. It is shown that deriving from the form of the boundary con- ditions with feedback we can obtain distributions of the light of relaxation, pre- turbulent and turbulent type.
Cite this paper
Krasnyuk, I.B. (2016) Impulse Spatial-Temporal Domains in Semiconductor Laser with Feedback. Journal of Applied Mathematics and Physics, 4, 1714-1730. http://dx.doi.org/10.4236/jamp.2016.49180
References
- 1. Faccio, D. (2012) Laser Pulse Analogues for Gravity and Analogues Hawking Radiation. Contemporary Physics, 93, 97-112.
http://dx.doi.org/10.1080/00107514.2011.642559 - 2. Jablan, M., Buljan, H., Manela, O. and Segev, M. (2007) Incoherent Modulation Instability in a Nonlinear Photonic Lattice. Optics Express, 15, 4623-4633.
http://dx.doi.org/10.1364/OE.15.004623 - 3. Mecozzi, A., D’Ottavi, A. and Hui, R. (1993) Nearly Degenerated Four-Wave Mixing in Disturbed Feedback Semiconductor Lasers Operating above Threshold. Journal of Quantum Electronics, 29, 1477-1487.
http://dx.doi.org/10.1109/3.234398 - 4. Sljacic, M., Segev, M., Coskuna, T.H., et al. (2000) Modulation Instability of Incoherent Beams in Non-Instantaneous Nonlinear Media. Physical Review Letters, 84, 467-470.
http://dx.doi.org/10.1103/PhysRevLett.84.467 - 5. Demircan, A., Amiranashvili, Sh. and Steinmeyer, G. (2011) Controlling Light by Light with an Optical Event Horizon. Physical Review Letters, 106, 163901-163907.
http://dx.doi.org/10.1103/PhysRevLett.106.163901 - 6. Webb, K.E., Erkintalo, M., Broderick, N.G.R., Dudley, J.M., Broderick, N.G.R., et al. (2014) Nonlinear Optics of Event Horizons. Nature Communications, 5, Article Number: 4969.
- 7. Coven, E.M. and Hedlung, G.A. (1980) Continuous Maps on the Interval Whose Periodic Points Form a Closed Set. Proceedings of the American Mathematical Society, 79, 127-133.
http://dx.doi.org/10.1090/S0002-9939-1980-0560598-7 - 8. Philbin, T.G., et al. (2008) Fiber-Optical Analog of the Event Horizon. Science, 319, 1367-1370.
http://dx.doi.org/10.1126/science.1153625 - 9. Haelterman, M. (1994) Modulational Instability, Periodic Waves and Black and White Vector Solitons Birefringent Kerr Media. Optics Communications, 11, 86-92.
http://dx.doi.org/10.1016/0030-4018(94)90144-9 - 10. Singh, S.P. and Singh, N. (2007) Nonlinear Effects in Optical Fibers Origin Management and Applications. Progress in Electromagnetic Research, 73, 249-275.
http://dx.doi.org/10.2528/PIER07040201 - 11. Buljan, H. and Segev, M. (2003) White-Light Solitons. Optics Letters, 28, 1239-1241.
http://dx.doi.org/10.1364/OL.28.001239 - 12. Sharkovsky, A.N., Maistrenko, Yu.L. and Romanenko, E.Yu. (1993) Difference Equations and Their Applications. Ser. Mathimatics and Its Applications. Kluwer Academic, Dordrecht.
- 13. Galenko, P. and Jou, D. (2005) Diffuse-Interface Model for Rapid Phase Transformations in with Relaxation of the Diffusion Flux in Nonequilibrium Systems. Physical Review E, 71, Article ID: 046125.
http://dx.doi.org/10.1103/PhysRevE.71.046125 - 14. Lecoq, N., Zapolsky, H. and Galenko, P. (2009) Evolution of the Structural Factor in a Hyperbolic Model of Spinodal Decomposition. Physical Review E, 177, 165-175.
- 15. Galenko, P. and Jou, D. (2009) Kinetic Contribution to the Fast Spinodal Decomposition Controlled by Diffusion. Physica A: Statistical Mechanics and Its Applications, 388, 3113-3123.
http://dx.doi.org/10.1016/j.physa.2009.04.003 - 16. Lecoq, N., Zapolsky, H. and Galenko, P. (2009) Evolution of the Structure Factor in a Hyperbolic Model of Spinodal Decomposition. European Physical Journal Special Topics, 179, 165-175.
http://dx.doi.org/10.1140/epjst/e2009-01173-8 - 17. Krasnyuk, I.B., Taranets, R.M. and Yurchenko, V.M. (2010) Pulse Structures Lamellar Type in the Bounded Polymeric Systems. Matematicheskoe Modelirovanie, 22, 65-81.
- 18. Krasnyuk, I.B. and Taranets, R.M. (2009) The Spatiotemporal Oscillations of Order Parameter for Isothermal Model of the Surface-Directed Spinodal Decomposition in Bounded Binary Mixtures. Research Letters in Physics, 2009, Article ID: 250203.
http://dx.doi.org/10.1155/2009/250203 - 19. Krasnyuk, I.B. and Taranets, R.M. (2011) The Spatial-Temporal Lamellar Structures in the Confined Ideal Polymer Blends. Journal of Statistical Physics, 145, 1485-1498.
http://dx.doi.org/10.1007/s10955-011-0378-5 - 20. Brandenburg, A., Käpylä P.J. and Mohammed, A. (2004) Non-Fickian Diffusion and Tau Approximation for Numerical Turbulence. Physic of Fluids, 16, 1020-1028.
http://dx.doi.org/10.1063/1.1651480 - 21. Maxwell, J.C. (1867) On the Dynamical Theory of Gases. Philosophical Transactions of the Royal Society, 157, 49-88.
http://dx.doi.org/10.1098/rstl.1867.0004 - 22. Libenson, M.N., Jakovlev, E.B. and Shandibina, R.I. (2008) The Interaction of Radiation with Matter C Substance (Optical Power). ITMO, St. Petersburg.
- 23. Mitchell, M., Chen, Z., Shih, M. and Segev, M. (1996) Self-Trapping of Partially Spatially Incoherent Light. Physical Review Letters, 77, 490-495.
http://dx.doi.org/10.1103/PhysRevLett.77.490