Received 7 October 2015; accepted 16 November 2015; published 19 November 2015

ABSTRACT

With the help of the method that combines the first kind of elliptic equation with the function transformation, some kinds of new composite solutions of a kind of coupled Schrödinger equation are constructed. First, a kind of function transformation is presented, and then the problem of solving solutions of a kind of coupled Schrödinger equation can be changed to the problem of solving solutions of the first kind of elliptic equation. Then, with the help of the conclusions of the Bäcklund transformation and so on of the first kind of elliptic equation, the new infinite sequence composite solutions of a kind of coupled Schrödinger equation are constructed. These solutions are consisting of two-soliton solutions and two-period solutions and so on.

Keywords:

A Kind of Coupled Schrödinger Equation, Function Transformation, Bäcklund Transformation, New Composite Solutions

1. Introduction

In many researches of the physical problems such as the high frequency movement of plasma, nonlinear optical, nonlinear dissipative system and fluid mechanics and so on, the Schrödinger type equations always appear. Many methods to solving solutions of these nonlinear evolution equations are presented [1] - [9] . Such as, liter- ature [1] [2] separately used the expand hyperbolic function method and the hyperbolic function type auxiliary equation method, obtained hyperbolic function type and trigonometric function type one-soliton solutions of Zakharov equation. Literature [3] used projection Riccati equation, obtaining hyperbolic function type one- soliton solutions of the nonlinear coupled Schrödinger-KdV equation. Literature [4] used Jacobi elliptic function expansion method, constructed new solutions of Davey-Stewartson equation. Literature [5] used the first kind of elliptic equation, constructed new solutions of Gross-Pilaevskii (G-P) equation. Literature [9] used auxiliary equation method, constructed new solutions of the following kind of Schrödinger equation.

(1)

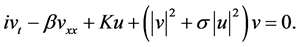(2)

Here, 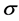is the relative cross-phase modulation coefficient and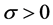, and K is the linear coupling coefficient accounting for possible twist of the fibre in the case where 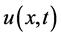and 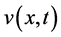represent orthogonal linear polarizations or elliptic deformation of the fibres cross-section if 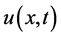and 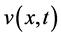correspond to circular polarizations.

Literature [1] - [9] obtained new finite one-soliton solutions of Schrödinger equation. Based on the auxiliary equation method [10] - [24] , the paper constructs the new infinite sequence composite exact solutions of a kind of coupled Schrödinger equation.

(3)

(4)

Here and are arbitrary constants.

First, a kind of function transformation is presented, and then the problem of solving solutions of a kind of coupled Schrödinger equation can be changed to the problem of solving solutions of the first kind of elliptic equation. Then, with the help of the conclusions of the Bäcklund transformation and so on of the first kind of elliptic equation, the new infinite sequence composite solutions of a kind of coupled Schrödinger equation are constructed. These solutions are new composite solutions consisting of two-soliton solutions, two-period solu- tions and the solutions composed of soliton solutions and period solutions composed in pairs by Riemann function, Jacobi elliptic function, hyperbolic function and trigonometric function.

2. The Relative Conclusions of the First Kind of Elliptic Equation

Then we put forward the Bäcklund transformation and so on new conclusions of the first kind of elliptic equation [21] (5).

(5)

Here a, b and c are constants.

2.1. The Solutions of the First Kind of Elliptic Equation

Case 1. The Riemann 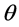function type new solutions of first kind of elliptic equation [22]

When, the first kind of elliptic equation (5) has the following solutions.

(6)

Here is a bivector, n is an integer. And,

Case 2. The Jacobi elliptic function type new solutions of the first kind of elliptic equation

According to the periodic of Jacobi elliptic function, many kinds of new solutions of the first kind of elliptic equation can be obtained, here we list some kinds of new solutions [21] .

When the first kind of elliptic Equation (5) has the following solutions.

(7)

(8)

(9)

Here Z is the assemblage of integer. are constants.

Case 3. The other new solutions of the first kind of elliptic equation

When the first kind of elliptic Equation (5) has the following solutions.

2.2. The Bäcklund Transformation of the First Kind of Elliptic Equation

If is the solution that not a constant of the first kind of elliptic Equation (5), then is also the solution of Equation (5).

(12)

Here a, b and c are the coefficients of first kind of elliptic Equation (5). l is an arbitrary constant not equal to zero.

If is the solution that not a constant of the first kind of elliptic Equation (5), then the following is also the solution of Equation (5).

(13)

Here a, b and are c the coefficients of first kind of elliptic Equation (5).

2.3. The Relative Conclusions of the Special First Kind of Elliptic Equation

When Equation (5) can be changed to Equation (15).

(14)

(15)

By the following transformation, Equation (15) can be changed to Riccati equation (17).

(16)

(17)

3. The Relative Conclusions of Riccati Equation

Then we put forward the relative conclusions of Riccati equation [23] [24] (18).

(18)

3.1. The Solutions of Riccati Equation

Riccati Equation (18) has the following normal solutions.

(19)

(20)

(21)

(22)

(23)

(24)

Here are arbitrary constants not equal to zero.

3.2. The Bäcklund Transformation of Riccati Equation

If is the solution of Riccati Equation (18), then the following is also the solution of Riccati Equation (18).

(25)

Here

.

and m are arbitrary constants not equal to zero. and are coefficients of Riccati Equation (18).

4. The New Infinite Sequence Composite Solutions of a Kind of Coupled Schrödinger Equation

4.1. A Kind of Coupled Schrödinger Equation and the First Kind of Elliptic Equation

By the following function transformation (26) (27), the problem of solving solutions of a kind of coupled Schrödinger Equation (3) (4) can be changed to the problem of solving solutions of two first kind of elliptic equation.

(26)

(27)

Here and are constants to be determined, and.

When, substituting function

transformation (26) and (27) into a kind of coupled Schrödinger Equation (3) (4) yields the following nonlinear ordinary differential equations.

(28)

(29)

The Equations (28) and (29) integrate once then we obtain

(30)

(31)

Here and are arbitrary constants.

4.2. The New Composite Solutions of a Kind of Coupled Schrödinger Equation

By the following superposition formula we obtain the new infinite sequence composite solutions of a kind of coupled Schrödinger Equation (3) (4).

(32)

(33)

Here and are determined by (30) and (31).

With the help of the relative conclusions the paper part two and part three put forward, we obtain the new infinite sequence solutions of the first kind of elliptic Equation (30) (31). Substituting these solutions separately into Formula (32) (33) yields the new infinite sequence composite solutions of a kind of coupled Schrödinger equation. These solutions are consisting of new solutions composed in pairs by Riemann function, Jacobi elliptic function, hyperbolic function and trigonometric function.

When, construct the new infinite sequence composite solutions.

When, by the following superposition formula, construct the new infinite sequence composite two- period solutions consisting of Riemann function, Jacobi elliptic function of a kind of coupled Schrödinger equation.

(34)

(35)

(36)

(37)

Case 1. The new composite two-period solutions composed by two Riemann functions.

Substituting the solutions obtained by superposition Formula (34) (36) together into Formula (32) (33) yields the new infinite sequence composite two-period solutions composed by two Riemann functions of a kind of coupled Schrödinger equation.

Case 2. The new composite two-period solutions composed by Riemann functions and Jacobi elliptic function.

Substituting the solutions obtained by superposition Formula (34) (37) (or (35) (36)) together into Formula (32) (33) yields the new infinite sequence composite two-period solutions composed by Riemann functions and Jacobi elliptic function of a kind of coupled Schrödinger equation.

Case 3. The new composite two-period solutions composed by two Jacobi elliptic functions.

Substituting the solutions obtained by superposition Formula (35) (37) together into Formula (32) (33) yields the new infinite sequence composite two-period solutions composed by two Jacobi elliptic functions of a kind of coupled Schrödinger equation.

When d₀ and d₁ are not all equal to zero, construct the new infinite sequence composite solutions.

When or we can obtain the following new infinite sequence composite solutions of a kind of coupled Schrödinger equation (not given here because of the space).

Case 1. The new infinite sequence composite solutions composed by Riemann function type period solution and exponential function soliton solution.

Case 2. The new infinite sequence composite solutions composed by Jacobi elliptic function period solution and exponential function soliton solution.

Case 3. The new infinite sequence composite two-soliton solutions composed by two exponential functions.

Case 4. The new infinite sequence composite solutions composed by exponential function type soliton solution and trigonometric function period solution.

Case 5. The new infinite sequence composite two-period solutions composed by Riemann function period solution and trigonometric function period solution.

Case 6. The new infinite sequence composite two-period solutions composed by Jacobi elliptic function period solution and trigonometric function period solution.

Case 7. The new infinite sequence composite two- period solutions composed by two trigonometric functions.

When, construct the new infinite sequence composite solutions.

Substituting the solutions obtained by the following superposition formula into Formula (32) (33) yields the new infinite sequence composite solutions of a kind of coupled Schrödinger equation.

(38)

(39)

(40)

(41)

Here, , ,. and m are arbitrary constants not equal to zero.

Case 1. The new infinite sequence composite two-soliton solutions composed by two exponential functions.

Substituting the solutions obtained by superposition formula (38),(40) together into formula (32),(33) yields the new infinite sequence composite two-soliton solutions composed by two exponential functions of a kind of coupled Schrödinger equation.

Case 2. The new infinite sequence composite solutions composed by exponential function type soliton solution and trigonometric function period solution.

Substituting the solutions obtained by superposition Formula (38) (41) (or (39),(40)) together into Formula (32) (33) yields the new infinite sequence composite solutions composed by exponential function type soliton solution and trigonometric function period solution of a kind of coupled Schrödinger equation.

Case 3. The new infinite sequence composite two-period solutions composed by two trigonometric functions.

Substituting the solutions obtained by superposition Formula (39) (41) together into Formula (32) (33) yields the new infinite sequence composite two-period solutions composed by two trigonometric functions of a kind of coupled Schrödinger equation.

5. Conclusions

Constructing the multiple-soliton solution of nonlinear evolution equation is a very important research of soliton theory. Auxiliary equation method has obtained many achievements in soliton theory. Such as: Literature [1] - [9] use auxiliary equation method and so on methods, obtained new finite one-soliton solutions consisting of expo- nential function, trigonometric function and rational function of Schrödinger equation.

Based on the achievements the auxiliary equation method has obtained, the paper constructs many kinds of new infinite sequence composite solutions of a kind of coupled Schrödinger Equation (3) (4). These solutions are new infinite sequence composite solutions composed in pairs by Riemann function, Jacobi elliptic func- tion, hyperbolic function and trigonometric function.

When, a kind of coupled Schrödinger Equation (3) (4) can be changed to Schrödinger Equation (1) (2). And when the coefficients of Equation (1) (2)

meet the condition that, So, according to the relative conclusions

that have been already obtained of a kind of coupled Schrödinger Equation (3) (4), we can construct the new infinite sequence composite solutions of Schrödinger Equation (1) (2).

Acknowledgements

Project supported by the Natural Natural Science Foundation of China (Grant No. 11361040), the Science Research Foundation of Institution of Higher Education of Inner Mongolia Autonomous Region, China (Grant No. NJZY12031) and the Natural Science Foundation of Inner Mongolia Autonomous Region, China (Grant No. 2015MS0128).

Cite this paper

Yili Na,Baojun Dong,  Taogetusang, (2015) Some Kinds of New Composite Solutions of a Kind of Coupled Schrödinger Equation. Journal of Applied Mathematics and Physics,03,1376-1385. doi: 10.4236/jamp.2015.311165

References

NOTES

^*Corresponding author.