Received 1 October 2015; accepted 8 December 2015; published 11 December 2015

ABSTRACT

The present study deals with the mixed convection MHD flow of a Casson nanofluid over a nonlinear permeable stretching sheet with viscous dissipation. The governing partial differential equations are transformed into nonlinear coupled ordinary differential equations with the help of suitable similarity transformations. These equations were then solved numerically by using an implicit finite difference method known as Keller-Box method. The effects of various parameters such as magnetic parameter (M), Casson parameter (b), local Grashoff number (Gr), local modified Grashoff number (Gc), nonlinear parameter (n), Eckert number (Ec) on velocity, temperature and concentration were discussed and presented graphically. It is found that a larger value of Casson parameter leads to decrease the velocity and temperature. Increase in the local Grashoff number reduces the temperature. Nanoparticle concentration is decreased for the larger values of local Modified Grashoff number. The numerical values of skin friction, Nusselt number and Sherwood number are presented in tables.

Keywords:

MHD, Nonlinear Permeable Stretching Sheet, Mixed Convection, Casson Fluid

1. Introduction

The study of boundary layer flows with the combined effects of heat and mass transfer over stretching or moving surfaces is quite essential due to its various applications in industrial and engineering processes, for example, in manufacture and extraction of polymer and rubber sheets. Sakiadis [1] [2] was the first to study the boundary layer flow over a continuously moving surface. The suitable similarity transformations were used to obtain numerical solution for the problem. Later this work was extended by Erickson et al. [3] in which the transverse velocity was non-zero, at the moving surface with heat and mass transfer in the boundary layer being taken into account.

Magyari and Keller [4] investigated the stretching problem of an incompressible fluid over a permeable wall. On the other hand, Gupta and Gupta [5], have mentioned that the stretching of the sheet may not necessarily be linear. In view of this, Vajravelu [6] studied the flow and heat transfer in a viscous fluid over a nonlinear stretching sheet. Bhargava et al. [7] examined the flow of a micro polar fluid over a nonlinear stretching sheet. Recently, Prasad et al. [8] studied the heat transfer analysis with the effect of mixed convection over a nonlinear stretching surface with variable fluid properties.

Nanofluid is a new type of heat transfer fluid which contains a base fluid and nanoparticles. The term nanofluid was proposed by Choi [9]. Nanofluids are used to increase the thermal conductivity of base fluids like water, ethylene glycol, propylene glycol, etc. They have various engineering and biomedical applications in cooling, cancer therapy and process industries. The pioneer work on the boundary layer flow of a nanofluid over a stretching sheet has been carried out by Khan and Pop [10] using Buongiorno’s model [11]. The boundary layer flow of a nanofluid induced by a stretching surface has drawn the attention of many researchers [12]-[14]. Rana and Bhargava [15] investigated the boundary layer flow of a nanofluid flow over a nonlinearly stretching sheet. Recently Mabood et al. [16] numerically studied the MHD boundary layer flow and heat transfer of nanofluids over a nonlinear stretching sheet.

In real life applications many materials like shampoos, printing ink, muds, condensed milk, paints, and tomato paste, etc., show different characters which cannot be understood by Newtonian theory. So to describe such type of fluids it is necessary to introduce the non-Newtonian fluids. The fluid which does not obey Newton’s law of viscosity is known as non Newtonian fluid. All the properties of non-Newtonian fluid cannot be expressed in a single non-Newtonian model; various models have been proposed in the literature and these models mainly categorized into three types namely differential, rate and integral type fluids.

In the year of 1959, a model presented in the flow of viscoelastic fluid by Casson which was known as a Casson fluid model. Casson fluid exhibits a yield stress. It is well known that Casson fluid is a shear thinning liquid which is assumed to have an infinite viscosity at zero rate of shear, a yield stress below which no flow occurs, and a zero viscosity at an infinite rate of shear, i.e., if a shear stress less than the yield stress is applied to the fluid it behaves like a solid, whereas if a shear stress greater than yield stress is applied it starts to move. Fredrickson [17] investigated the steady flow behavior of a Casson fluid in a tube. M. Nakamura et al. [18], studied the flow of a non-Newtonian fluid through an axisymmetric stenosis numerically. Mustafa et al. [19] studied and solved analytically using homotopy analysis method (HAM) for the problem unsteady boundary layer flow with heat transfer of a Casson fluid over a moving flat plate with a parallel free stream and the concept of MHD flow of the Casson fluid model over an exponentially shrinking sheet has been presented by Nadeem et al. [20]. An exact solution of the steady boundary layer flow of Casson fluid over a stretching or shrinking sheet was studied by Bhattacharyya et al. [21], and analytical solution has been given by Krishnendu Bhattacharyya et al. [22] for the problem MHD boundary layer flow of Casson fluid over stretching/shrinking sheet with wall mass transfer whereas Swati Mukhopadhyay [23] studied Casson fluid flow and heat transfer over a nonlinearly stretching surface. On the other hand Peri K. Kameswaran et al. [24] investigated and presented Dual solutions of Casson fluid flow over a stretching or shrinking sheet. Rizwan Ul Haq et al. [25] studied the flow of Casson nanofluid over an exponential shrinking sheet with convective heat transfer and MHD effects. Recently the MHD flow of a Casson nanofluid with viscous dissipation over an exponentially stretching sheet by considering convective conditions is studied by T. Hussain et al. [26]. M. Mustafa and Junaid Ahmad Khan [27], discussed a model for the flow of Casson nanofluid past a nonlinearly stretching sheet considering magnetic field effects.

From the above literature, no investigation has been reported for the mixed convection MHD flow of a Casson nanofluid over a nonlinear permeable stretching sheet with viscous dissipation. The basic governing equations are converted into ordinary differential equations by applying suitable similarity transformations and those equations were solved numerically by using an implicit finite difference method called as the Keller box method.

The aim of the present study is to investigate nanoparticle analysis for the Casson fluid model and the effect of Casson parameter on velocity, temperature and concentration fields illustrated with the help of graphical representations.

2. Flow Analysis

Let us consider the two dimensional steady incompressible flow of a Casson nanofluid induced by a nonlinearly stretching sheet which is placed at y = 0. The flow is confined to y > 0. By keeping the origin is fixed and sheet is stretched with nonlinear velocity, where is nonlinear stretching parameter and >0, x is the coordinate measured along the stretching surface. The nanofluid flows at, where y is the coordinate normal to the surface. The fluid is electrically conducted due to an applied magnetic field normal to the stretching sheet. The magnetic Reynolds number is assumed small and so the induced magnetic field can be considered to be negligible. The wall temperature and the nanoparticle fraction are assumed constant at the stretching surface. When y tends to infinity, the ambient values of temperature and nanoparticle fraction are denoted by and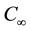, respectively. It is important to note that the constant temperature and the nanoparticle fraction of the stretching surface and 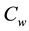are assumed to be greater than the ambient temperature and nanoparticle fraction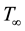, 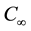respectively.

We also assume that the rheological equation of extra stress tensor () for an isotropic and incompressible flow of a Casson fluid can be written as

where 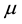is the dynamic viscosity and 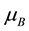is the plastic dynamic viscosity of the non-Newtonian fluid, is the yield stress of fluid, is the product of the component of deformation rate of component and, is the critical value of based on non-Newtonian model.

In steady two dimensional flow the velocity field is given by, the temperature distribution and the nanoparticle volume fraction. Under the above considerations the equations governing the mixed convection MHD flow of Casson nanofluid past a nonlinearly stretching sheet with viscous dissipation are:

(1)

(2)

(3)

(4)

The boundary conditions for the above flow are

(5)

Here u and v are the velocity components in the x-and y-direction respectively, is thermal diffu-

sivity, is electrical conductivity, v is the kinematic viscosity, is the Casson fluid parameter, is the density of the base fluid, g is the acceleration due to gravity, is the coefficient of thermal expansion, is the coefficient of expansion with concentration, is the Brownian diffusion coefficient and is the

thermophoresis diffusion coefficient, is the ratio of nanoparticle heat capacity and the base fluid

heat capacity, c is the volumetric volume coefficient, is the density of the particles, and C is rescaled nanoparticle volume fraction. We assume that the variable magnetic field is of the form.

Rana and Bhargava [15] introduced the following transformations.

(6)

And assume, where S is the suction parameter.

By substituting the above transformations (6) in Equations (2)-(4) the governing equations are reduced to

(7)

(8)

(9)

Then the transformed boundary conditions are

(10)

(11)

where prime denotes differentiation with respect to. The physical parameters involved in the above equa-

tions are defined as is Prandtl number, is Lewis number, is the

Brownian motion parameter, is the thermophoresis parameter, is magnetic parameter, Eckert number, is the local Grashof number and is the local modified Grashof number.

The quantities of the skin friction coefficient, the local Nusselt number and local Sherwood number given as below:

, where (12)

where k is the thermal conductivity of the nanofluid and are the heat and mass fluxes at the surface respectively given by

(13)

By substituting Equation (6) into Equations (12)-(13), we will get

where which is the local Reynolds number.

3. Numerical Solution

As the ordinary differential Equations (7)-(9) are non-linear, we cannot get the closed form solution. Hence the equations subject to the boundary conditions (10)-(11) are solved numerically using Keller-Box method, as men- tioned by Cebeci and Bradshaw [28] . According to Vajravelu et al. [29] , the main steps involved in this method to get the numerical solutions are given below.

1) The Ordinary Differential Equations are converted into a system of first order equations.

2) Write the finite differences for the first order equations.

3) Linearize the algebraic equations by using Newton’s method and write them in vector form.

4) Solve the linearized difference equations by the block tridiagonal elimination technique.

To get the accuracy of this method the appropriate initial guesses have been chosen.

The following initial guesses are chosen.

4. Results and Discussions

The aim of the present study is to analyze the effects of various emerging parameters on velocity, temperature and concentration profiles over a nonlinearly stretching sheet. The similarity transformations were used to transform the governing partial differential equations to nonlinear coupled ordinary differential equations. Later, those equations were solved by using an implicit finite difference technique called as Keller-Box method.

The results obtained in the study are compared with the existing literature and found in good agreement which is presented in the Table 1.

Numerical values of skin friction, Nusselt number and Sherwood number are presented in the Table 2, Table 3 and Table 4 respectively.

Figure 1 explains the variations in the velocity with respect to the magnetic parameter M, when M increases the velocity decreases this is because the transverse magnetic field creates the Lorentz forces. It is a resistive force similar to the drag force which will result in the deceleration of the flow.

The variations in velocity with respect to Casson fluid parameter presented in the Figure 2 it was found that increase in increases the fluid viscosity this causes the decreasing in fluid velocity. Increase in nonlinear stretching parameter makes the velocity of the fluid flow to be decreased. This result is presented in the Figure 3.

Figure 4 illustrates the variations in velocity with respect to suction parameter . Due to increase of suction parameter the amount of fluid particles were drawn into the wall hence the boundary layer decreases. Figure 5 and Figure 6 visualizes the effects on the velocity profile with respect to (local Grashoff number), (local modified Grashoff number) and it was found that the increase in the increases the velocity whereas increase in increases the velocity of the fluid.

Figure 7 indicates that the temperature profile for different values of yield stress/Casson fluid parameter. It can be seen that increasing the values of Casson fluid parameter reduces the temperature and thermal boundary layer thickness.

Figure 8 exhibits the influence of thermoporesis parameter Nt on temperature distribution.

The enhancement of thermophoretic effects causes the migration of nanoparticles from the hot surface to the cold ambient fluid as a consequence of this the temperature increases in the boundary layer.

From Figure 9 it is observed that the increase in the Brownion motion parameter increases the temperature.

From Figure 10 it is observed that the reversal flow happened this is because of the temperature enhancement occurs as heat energy is stored in the fluid due to frictional heating. Whereas from Figure 11 it is observed that temperature slightly decreases with increasing values of local Grashoff number.

Figure 12 and Figure 13 prepared to show the influence of thermoporesis parameter Nt and Brownian motion parameter on nanoparticle concentration. From the figures it is clear that nanoparticle concentration increases with increasing values of thermoporetic parameter Nt. On the other hand Brownian motion serves to warm the boundary layer and simultaneously increases particle displacement away from the fluid regime, thereby accounting for the reduced concentration magnitudes. The larger values of Brownian motion parameter, it reduces the nanoparticle concentration.

Figure 14 presents the effect of Lewis number on dimensionless nanoparticle concentration. An increase in Lewis values will reduce the profile of nanoparticle concentration, and larger values will also suppress concentration profile. From Figure 15 it is noticed that nanoparticle concentration is a decreasing function of local modified Grashoff number.

5. Conclusions

A numerical study was investigated for the mixed convection MHD flow of a Casson nanofluid over a nonlinear permeable stretching sheet with viscous dissipation with the help of an implicit finite difference method known as Keller-Box method. A parametric study is performed to explore the effects of various governing parameters on the fluid flow and heat transfer characteristic. Following conclusions give the brief results of the present study.

1) Increase in the values of magnetic parameter decreases the velocity profile.

2) Increase in nonlinear stretching parameter n decreases the velocity profile.

3) It is found that larger values of Casson parameter lead to decrease the velocity and temperature.

4) Temperature is enhanced for the higher values of Eckert number.

5) Increase in the local Grashoff number reduces the temperature.

6) Nanoparticle concentration is decreased for the larger values of local modified Grashoff number.

7) Nanoparticle concentration is enhanced for the higher values of Lewis number.

Acknowledgements

This research was supported by University Grants Commission-India under Faculty Development Programme The author gratefully acknowledges the support of UGC.

Cite this paper

PrabhakarBesthapu,ShankerBandari, (2015) Mixed Convection MHD Flow of a Casson Nanofluid over a Nonlinear Permeable Stretching Sheet with Viscous Dissipation. Journal of Applied Mathematics and Physics,03,1580-1593. doi: 10.4236/jamp.2015.312182

References