Received 14 March 2015; accepted 5 September 2015; published 8 September 2015

ABSTRACT

In this paper, we study properties of solutions to doubly nonlinear reaction-diffusion systems with variable density and source. We demonstrate the possibilities of the self-similar approach to studying the qualitative properties of solutions of such reaction-diffusion systems. We also study the finite speed of propagation (FSP) properties of solutions, an asymptotic behavior of the compactly supported solutions and free boundary asymptotic solutions in quick diffusive and critical cases.

Keywords:

Double Nonlinear Reaction-Diffusion Equation, Self-Similar Solution, Asymptotics

1. Introduction

Let’s consider properties of the Cauchy problem for the following system of nonlinear reaction-diffusion equations in the domain

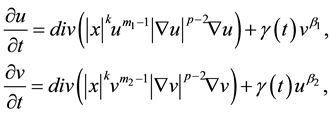(1)

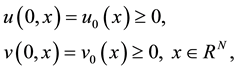(2)

where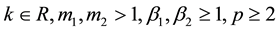 are given positive numbers, and, ,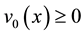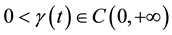. System (1) describes different physical process in two componential inhomogeneous nonlinear environments. For example, the processes of the reaction-diffusion, heat conductivity, polytrophic filtration of liquids and gas with a source power which is equal to 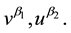Cases, when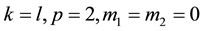, were considered in [1] -[7] .

The system (1) in the domain, where 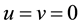is degenerated, and in the domain of degeneration it may not have the classical solution. Therefore, we study the weak solutions of system (1) which also have physical sense: and 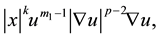satisfy some integral identity in the sense of distribution [1] . For the solution of system (1) there are phenomena of the finite speed of a propagation (FSP). That is, there are functions that satisfy 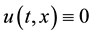and at and. In the case of, a solution of problems (1), (2) is called space localization of a disturbance. The surfaces and are called a free boundary or a front, respectively.

The process of the reaction-diffusion with double nonlinearity in the case of one equation has been investigated by many authors (see [8] -[15] and the references therein). FSP and blow-up property for equations with variable density

was established in [8] [9] . An asymptotic of self-similar solutions was studied in [15] . Martynenko and Tedeev [10] [11] studied the Cauchy problem for the following two equations with variable coefficients:

and

where or

They showed that under some restrictions to the parameters and initial data, any nontrivial solution to the Cauchy problem blows up in finite time. Moreover, the authors established a sharp universal estimate of the solution near the blow-up point.

It is well know that qualitative properties of solutions of the equation similar to (1) have not been investigated thoroughly. There are some results in [1] -[6] corresponding to the case.

In the present work, the qualitative properties of solutions of system (1) are studied based on the self-similar and approximately self-similar approach. We establish one way of construction of the critical exponent and property finite speed of perturbation (FSP) for system (1). An asymptotic property of compactly supported solutions (c.s.s.) of the considered problem and the behavior of the free boundary for the case are obtained. We prove the existence of solution with finite property. An asymptotic of a self-similar solution for the fast diffusion case and a critical case are also studied.

2. Approximate Self-Similar and Self-Similar Equations

Below we provide a method of nonlinear splitting for construction of self-similar and approximately self-similar equation. For construction of the self-similar and approximately self-similar solutions of system (1) we search the solutions in the form

(3)

Here, we obtain as

Which are the solutions of following equations

Substituting (3), the system (1) is reduced to the following system of equations

(4)

where the functions are chosen as following

(5)

It is easy to establish that the system (4) has approximately self-similar solution of kind

(6)

where and the functions satisfies the approximately self-similar system equations

(7)

It is easy to prove that as

(8)

for, where -Hardy’s body [2] , are constants. In this case, it is easy to show that system (1) becomes a self-similar for a sufficient large t. Therefore it is possible to consider the system (7) as an asymptotically self-similar system of equation corresponding to system (1). In particular case, when approximately self-similar systems (7) will be as self-similar if

(9)

In this case for the functions we have the following self-similar system of equation in “radial” form

(10)

where

In the case or in (10), the properties of the different solutions as computing aspects of the system Equation (10) were studied by many authors [8] -[15] . In singular, one equation case, when the existence of positive solutions of the Equation (10) was studied in [14] .

3. Slowly Diffusion Case:

3.1. A Global Solvability of Solutions

(11)

where

In the case,

where

Fujita type critical exponent for the system (1) is numerical parameters for which the following equality holds:

(12)

This result consists of the result of Escobedo, Herero [15] for the case when in (1).

Theorem 1. (A global solvability). Assume,

Then for sufficiently small the followings holds

(13)

where the functions defined as above, are constants.

Proof. For proving theorem 1 we use a comparison principle. As a comparison solution we take the functions where

It is easy to check that

If

Then we have

In order to apply a comparison principle we note that in

Since

Therefore,

Then according to the hypotheses of Theorem 1 and comparison principle we have

if

The proof of the theorem is complete.

We notice that if

then

It means that

if

3.2. Property of Finite Speed of a Perturbation

Corollary 1. Suppose that the hypotheses of Theorem 1 holds. Then a solution of the problems (1), (2) has FSP property.

Indeed, for a weak solution of the problems (1), (2) we have

It follows that

where It means that the solution of the problems (1), (2) have FSP

property.

Critical case. The case will be called a critical case.

Theorem 2. Let Then for sufficiently small

the problems (1), (2) have global solution and the following inequalities in Q hold

(14)

here

Proof. Proof of the theorem is based on the comparison principle. We take for comparison the functions

where

It is easy to check that

From the hypothesis of Theorem 2 and last expressions we have

if the constants such that

This inequality due to the comparison principle completes the proof of the theorem.

Value for which

corresponds to Fujita type critical exponent proved earlier by Escobedo, Herrero [15] for the case p = 2.

4. Asymptotic of the Self-Similar Solutions

Now we study asymptotic of the weak compact supported solutions (c.s.s.) of the system (10) when Consider this system equation with boundary condition

(15)

where.

The existence of a self-similar weak c.s. solution for the problems (10), (15) in the case was studied in [6] where the authors obtained conditions for existence of the c.s. solution.

We seek solution of the system (10) in the form

(16)

where

(17)

Theorem 3. Assume that Then the weak compactly support solutions

(c.s.s) of the system (10) as has asymptotic

where the coefficients satisfied to system of the algebraic equations

Proof. It is easy to check that

and

We will show that the functions should be main member of asymptotic of solution of the system (10). For this goal we search the solution of system (10) in the form

By using expression (10) it is easy to cheek that

Therefore according transformation (16) the system (10) reduced to the system

(18)

where

Analysis of solution of last system shows that as where constants are the solutions of the algebraic system equations

The proof of the theorem is complete.

5. Quick Diffusion Case:

Theorem 4. Let Then regular (quenching) solution of the system (10) as has asymptotic

Here

1) if then the coefficients are the roots of the nonlinear system of the algebraic equations

(19)

2) if then the coefficients are the roots of the nonlinear system of the algebraic equations

(20)

Proof. We will seek a solution of system (10) in following form

(21)

Since

By substituting (21) into (10) we get

(22)

where

Analyzing of solutions system (22) when we conclude that the solutions of this system where constants are solutions of the algebraic system (19), (20).

Cite this paper

MersaidAripov,Shakhlo A.Sadullaeva, (2015) Qualitative Properties of Solutions of a Doubly Nonlinear Reaction-Diffusion System with a Source. Journal of Applied Mathematics and Physics,03,1090-1099. doi: 10.4236/jamp.2015.39135

References