Journal of Applied Mathematics and Physics
Vol.2 No.8(2014), Article ID:47575,10 pages
DOI:10.4236/jamp.2014.28083
Growth Stratification Applied to Prognosis of Diametric Structure in Araucaria Forest
Sylvio Péllico Netto*, Ângelo Augusto Ebling, Emanuel José Gomes de Araújo
Department of Forest Science, University Federal of Paraná, Curitiba, Brazil
Email: *sylviopelliconetto@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 April 2014; revised 20 May 2014; accepted 3 June 2014
ABSTRACT
The forest management, in broad terms, covers a set of information and activities related to the growth and production of plantations or from heterogeneous forests. If on one hand forest plantation presents homogeneous dendrometric characteristics, on the other hand in heterogeneous forests such a configuration does not exist, which requires the application of essential mathematical estimates for the forest management planning, for example, the prognosis of diametric structure. In this respect, refinements can be tested in traditionally used mathematical models, aiming at more accurate results. These facts substantiate the following hypotheses: the stratification of the diameter increments can provide estimates with greater accuracy and more precise results for the prognosis. With the stratification of diameter increment made it possible to get better results for the prognosis for a 4-year period, allowing the forest manager to better work with estimators either for diameter classes as well as for the forest to be managed. Using the data structure of trees (DBH ≥ 9.5 cm) of the National Forest of Sao Francisco de Paula, RS, Brazil, the diameter increment of species was stratified into four statistically different strata. Using data sampled between the years of 2000 to 2004, it was carried out prognosis for the year 2008, using the stratified and not stratified data. The estimates were compared with the observed values by the Kolmogorov-Smirnov (K-S) test, which attested goodness of fit only for the estimates from the stratified values. The prognosis estimated by means of stratified values also showed more accurate results, because the stratified variance was reduced nine times when compared with that obtained with the prognosis made without stratified data and to determine the Quotient of De Liocourt. Thus, the diameter growth stratification indicated to be effective to generate more accurate prognosis.
Keywords:Diameter Projection, Forest Management, Heterogeneous Forest

1. Introduction
Brazil has the second largest forest area in the world, covering 516 million hectares and from this total 98.7% is made up of natural forests [1] , which highlights the importance of the conservation and rational exploitation of forest resources, as a way to leverage the national development. However, sustainable management practices rely on studies for its effectiveness and also that enables efficiency in mechanisms traditionally employed.
Methodologies consist of mathematical models to generate prognosis, as the ratio of moving diameters, which are dependent on information related to forest dynamics [2] and allow subsidizing information for the effectuation of a rational exploitation of heterogeneous forests. However, refinements can be applied to these models, aiming at more accurate estimates [3] .
Whereas stratification has the goal to reduce the variance of a sample, resulting in subpopulations with greater homogeneity [4] , the application of the ratio of change for making prognosis, including the number of recruitment and mortality, which is based on the diameter growth model [5] ; these facts substantiate our main hypotheses: the stratification of the diameter increments can provide estimates with greater accuracy and more precise results for the prognosis.
Although stratification of height is of great importance in phytosociological studies and in forest management and often used by managers [6] , stratification of diameter is still little employed in such studies. The delimitation of strata or subpopulations, defined as a function of the species diameter growth, may also be useful in projects for rehabilitation and restoration of degraded areas, in which the choice of species will be more appropriate if it is, at our disposal, a broader knowledge about them [7] . Also relevant, the groups of species separated by growth can guide the planning of projects related to the carbon storage, as well as better clarify the use of silvicultural activities and practices demanded by the forest management.
2. Methodology
2.1. Experimental Area
The study was conducted in the National Forest of Sao Francisco de Paula, located between the coordinates 29˚24' and 29˚27' South latitude and 50˚22' and 50˚25' West longitude, in the mesoregion northeast of the State of Rio Grande do Sul, Microregion of Vacaria, in Brazil. The average altitude site is 900 meters above the sea level, ranging this value ±300 meters. The soils that characterize the region are classified as Haplumbrept, Argiudoll, Udorthent [8] , derived from basic and acidic effusive rocks of the Serra Geral Formation [9] .
In accordance with the global classification of climatic types developed by Köppen, the climate of the region is of type Cfb, mesothermal and super humid, with mild summer and cold winter. The formation of frost is frequent, with snowfall in the colder months [10] .
The predominant vegetation of the National Forest area is the Araucaria Forest or Mixed Tropical Forest, monitored by means of continuous forest inventory with the application of sampling with total replacement, which encompasses a total sample area of 10 permanent plots with an area of 1 ha (100 × 100 m) each, remeasured annually since the year 2000. All arboreal individuals (trees with diameter at breast height ≥9.5 cm) included in sample area were botanically identified and had their dendrometric information measured.
2.2. Data Collection and Stratification
Taking the diameters collected in a specific period, their periodic increments were
calculated and subsequently the mean of the periodic increment
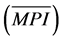 for each species. In order to make the population of species more consistent, only
those that met a minimum of 10 individuals in the sample were considered. After
that it was defined the population of species E
for each species. In order to make the population of species more consistent, only
those that met a minimum of 10 individuals in the sample were considered. After
that it was defined the population of species E
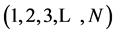 from which a random variable Xi was measured, the (MPI) per individual
of each species, such that it was characterized for each species a population of
sample values Pij, such that
from which a random variable Xi was measured, the (MPI) per individual
of each species, such that it was characterized for each species a population of
sample values Pij, such that
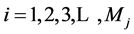 individuals and
individuals and
![]() species, i.e.,
species, i.e.,
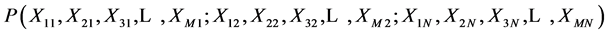 , in which the arithmetic mean and variance per species
are given by
, in which the arithmetic mean and variance per species
are given by
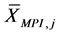 and
and
![]() respectively.
respectively.
The stratification of growth was established taking as criterion the quartiles formalized
on the basis of the arithmetic mean of the growth of species
 and the standard deviation
and the standard deviation . In this way, the population of species will
be fractioned into L strata, such that each one of them will be delimited as Eh
. In this way, the population of species will
be fractioned into L strata, such that each one of them will be delimited as Eh , in that Nh is the number of species
of each stratum and, consequently,
, in that Nh is the number of species
of each stratum and, consequently,
 and
and![]() . Thus, the strata are composed respectively
of Ejh
. Thus, the strata are composed respectively
of Ejh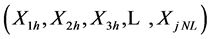 .
.
This procedure of stratification was decided as demonstrated by Cochran (1963), in that, if the full range of variation of MPI’s is expressed by (EL − E0), the separation of the strata (Eh − Eh+1), being taken of constant size, will minimize the sum of squares due to stratification and, consequently, it will result in the minimum stratified variance of mean, i.e., maximum accuracy by application of stratification.
It was proposed four strata for growth evaluation: E1, E2,
E3 and E4, which is composed, respectively, of the smallest
to the largest increments. The stratum E1 was composed by species with
periodic mean increment
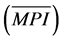 less than the average growth of all species minus one standard deviation
less than the average growth of all species minus one standard deviation , with mean
, with mean
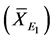 and variance
and variance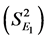 . The stratum E2, composed by the
species with higher growth than E1 up to the limit of one standard deviation
above that value
. The stratum E2, composed by the
species with higher growth than E1 up to the limit of one standard deviation
above that value , with mean
, with mean
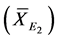 and variance
and variance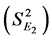 . The same was set alongside to the third
stratum E3, composed by species of growth higher than the E2,
up to the limit of one standard deviation above that value
. The same was set alongside to the third
stratum E3, composed by species of growth higher than the E2,
up to the limit of one standard deviation above that value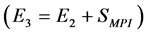 , with mean
, with mean
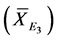 and variance
and variance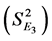 . The fourth stratum E4 is understood
to have the grater values than E3, with mean
. The fourth stratum E4 is understood
to have the grater values than E3, with mean
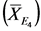 and variance
and variance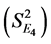 . It was calculated the variance of the increments
before stratification
. It was calculated the variance of the increments
before stratification
 and after stratification
and after stratification .
.
Such parameters for the stratified population will be obtained as are expressed in (1) for the stratified mean and in (2) for the stratified variance.
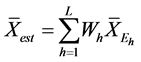 where
where
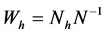 (1)
(1)
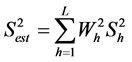 (2)
(2)
2.3. Statistical Evaluation of the Population
The normality of the data set was checked by the Shapiro-Wilk test (W), and the homogeneity of variances by Hartley test (Fmax). If null hypotheses H0 is rejected (normal distribution and homogenous variance), it will be applied to the data set the appropriate transformations using the method of Box and Cox, defined as:
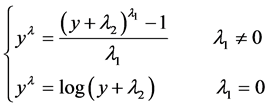
where:
![]() = transformed value;
= transformed value;
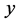 = observed value;
= observed value;
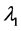 = transforming power of the data set;
= transforming power of the data set;
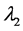 = parameter to regulate the distribution fitting.
= parameter to regulate the distribution fitting.
Twenty one values were selected for
 inserted between the interval of (−5, 5) [11]
. The value of
inserted between the interval of (−5, 5) [11]
. The value of
 selected for the transformation is that which provide the lowest value for Fmax.
As the set of observed data occurs in the interval (0, 1), taking
selected for the transformation is that which provide the lowest value for Fmax.
As the set of observed data occurs in the interval (0, 1), taking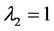 , it is possible to obtain values on a scale
more favorable for the data transformation.
, it is possible to obtain values on a scale
more favorable for the data transformation.
Due to stratification, an allocation of sample intensities became different per stratum and, consequently, with different degrees of freedom in each one of them; that is why it has been decided to use the Satterthwaite’s method to calculate the number of degrees of freedom [12] , as weighted mean and is presented in (3):
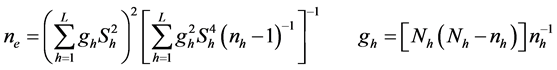 (3)
(3)
where:
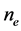 = weighted mean for the number of degrees of freedom;
= weighted mean for the number of degrees of freedom;
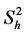 = Variance per stratum;
= Variance per stratum;
Nh = potential number of species (Eh);
nh = number of species allocated per stratum;
The value of
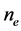 must occur between the smallest of the values
must occur between the smallest of the values
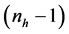 and shall not exceed their sum [13] .
and shall not exceed their sum [13] .
To carry out the statistical analysis between the strata means, it was applied the analysis of variance (ANOVA), whereas a completely randomized design with four treatments (strata) and different number of replicates, followed by application of Tukey’s test, when identified significant statistical differences between strata means.
The methodology used to accomplish the prognoses was the ratio of moving diameters, used as a theory of stand projection tables applied to native forests [5] . Succinct manner, the application of such methodology consists in the migration of the number of trees to upper diameter classes, in function of the average diameter growth per class, considering the increases and decreases from recruitments and mortalities (Table 1). This model has been used successfully in prognosis works in native forests in Brazil, with best results than those obtained with the application of the Markov Chain model [14] . The data employed for stratification refer to the sampling period from 2000 to 2004.
With the purpose to verify the effect of stratification on the results of the prognosis, it was first predicted the forest structure, employing the stratified data and, subsequently, it was held the prognosis with the raw data, without stratification. Both prognoses were made for the year 2008. The forecasted values were compared with the observed ones by application of the Kolmogorov-Smirnov test (K-S) at 95% probability, whose null hypothesis (H0) consists in goodness of fit between projected and observed data.
Complementary to the goodness of fit test, due to its importance in structural evaluations and in the effectiveness of the forest management practices, it was evaluated the behavior of the De Liocourt Quotient (q) between the estimated and observed values.
3. Discussion of the Results
As population of species was defined E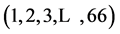 , of which the random variable Xi was
calculated
, of which the random variable Xi was
calculated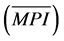 such that these mean values became associated with
all species of the population E
such that these mean values became associated with
all species of the population E
 with arithmetic mean
with arithmetic mean
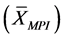 and variance
and variance .
.
The stratification of diameter growth was established taking as criterion the quartiles
based on the average growth of the species
 and the standard deviation
and the standard deviation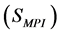 . In this way, the population E of the species was
fractionated into 4 strata, such that each one of them was delimited as N1
= 8; N2 = 29; N3 = 18 and N4 = 11.
. In this way, the population E of the species was
fractionated into 4 strata, such that each one of them was delimited as N1
= 8; N2 = 29; N3 = 18 and N4 = 11.
The periodic mean diameter increment
 for the forest was
for the forest was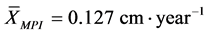 , a value lower than the average of 0.210 cm×year−1
found by Figueiredo Filho et al. in its bibliographical searches related to studies
conducted in the Araucaria Forest [15] . The difference
between the values found for increment can be explained, because the diameter growth
is interpreted as a response to the availability of essential factors in the en
, a value lower than the average of 0.210 cm×year−1
found by Figueiredo Filho et al. in its bibliographical searches related to studies
conducted in the Araucaria Forest [15] . The difference
between the values found for increment can be explained, because the diameter growth
is interpreted as a response to the availability of essential factors in the en
1indicates the ratio of the average growth by the width of the diameter class; 2trees that remained in the same class; 3,4number of trees that died and were recruited, respectively, during the observed period.
vironment [16] [17] , plus the characteristics related to different stages of forest succession in a phytogeographical unit.
Taking as basis for stratifying the average growth rate
 and the standard deviation between the species (SMPI = 0.071 cm×year−1),
the limits of the strata were defined as: E1 for the values of
and the standard deviation between the species (SMPI = 0.071 cm×year−1),
the limits of the strata were defined as: E1 for the values of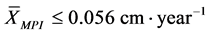 ; E2 for values of
; E2 for values of ; E3 for the values of
; E3 for the values of
 and E4 for the values of
and E4 for the values of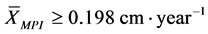 , as shown in Table2
, as shown in Table2
The stratum of greater representativeness was the E2, corresponding to
44% of the species evaluated, followed by E3 (27% of species), E4
(17% of species) and E1 (12% of species). The growth mean values of the
respective strata were: ;
;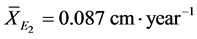 ;
;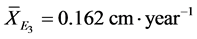 ;
;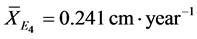 .
.
The variance for the population without stratification resulted in , a value nine times higher than the stratified variance
, a value nine times higher than the stratified variance . The strata 1 to 4 presented variances of:
. The strata 1 to 4 presented variances of: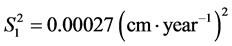 ;
;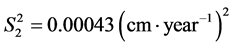 ;
;
 and
and
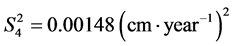 . Consequently, groups of greater growth homogeneity were obtained
with the application of stratification inside the total population.
. Consequently, groups of greater growth homogeneity were obtained
with the application of stratification inside the total population.
Each stratified data set followed the normal distribution, evaluated by the Shapiro-Wilk
test (W) at 95% probability. The effective number of degrees of freedom calculated
by Satterthwaite’s method was 41 (ne = 40.4). The variances were not
homogeneous (heteroscedasticity), with rejection of the null hypothesis H0
by Hartley’s test (Fcalc = 5.49 > Ftab;0.01 = 2.97).
The data set was then subjected to Box-Cox’s transformation, with a value of
 equal to −3.5, which led to the lowest value for Fcalc, ensured
the homogeneity of variances (Fcalc = 2.58 <
equal to −3.5, which led to the lowest value for Fcalc, ensured
the homogeneity of variances (Fcalc = 2.58 <
Ftab;0.01 = 2.97) and remained normally distributed. Consequently,
detected heteroscedasticity of the variances within strata in which the total population
of
 was allocated, the application of Box and Cox transformation, using the prospective
simulation proposed by Draper and Smith to identify the most appropriate root to
be used in the process, resulted in total efficiency to get homoscedasticity of
variances (Figure 1).
was allocated, the application of Box and Cox transformation, using the prospective
simulation proposed by Draper and Smith to identify the most appropriate root to
be used in the process, resulted in total efficiency to get homoscedasticity of
variances (Figure 1).
By means of analysis of variance, it can be observed that there are statistical differences between the strata (Table 3). Therefore, it is inferred that the auto ecological characteristics of each species that composes the plant community favor decisively the formation of groups with different diameter growth. Consequently, the stratification of diameter growth reduced the variance nine times, enabling the formation of groups of greater homogeneity and statistically different between themselves.
The Tukey’s test indicated statistical differences between means of the strata (Table 4). Assuming that the differences between strata represent species with different growth potential, the choice of species belonging to a particular stratum may favor the accomplishment of the objectives of forest management, where growth has an important meaning. Consequently, the allocation of species in strata favors the decisions in forestry projects, in which the diameter increment is one of the relevant variables for the establishment of activities and delineation of targets.
Whereas the models of production meets a set of criteria that assist in decision making for the forest planning [18] , it was evaluated the prognosis of the diametric structure from the stratified data and without stratification, by means of the methodology of ratio of change, which is based on diameter’s growth and migration of them between diameter classes, unlike the Markov chain, which considers only the enumeration of individuals that move between classes. The predicted values in each stratum and total, which represents the sum of stratified estimates, are presented in Figure 2.
Meyer et al. in their studies that support the sustainable management, about the diameter distribution in hete-
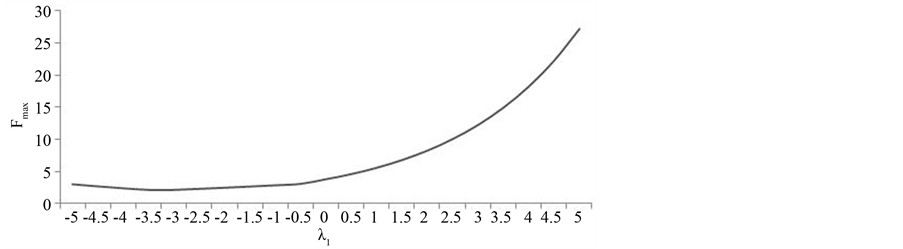
Figure 1. Behavior of the value Fmax as a function of the values of λ1 tested.
Table 3. Analysis of variance for stratification in Araucaria Forest.
**Significant at 1% level of probability.
Table 4. Tukey’s test at 95% probability between the strata means.
*Means followed by same letter do not differ from each other by Tukey’s test at 95% probability.
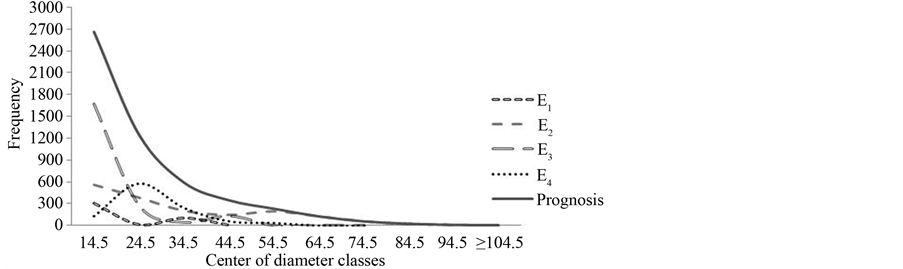
Figure 2. Projected frequency distribution per stratum and for the population.
rogeneous all age forests, refer to a pattern of decreasing exponential distribution to the extent to which diameter classes advance [19] . However, such a pattern was only found in the sum of stratified subpopulations, which generated the projected distribution. Each stratum presented differentiated settings in their distributions, justified by the auto ecological and synecological characteristics of the species of each stratum.
The K-S test (Dcalc = 0.00949 < Dtab;0.95 = 0.01855) attested goodness of fit of projected values from stratified data, however the projected values from no stratified data did not present goodness of fit to the observed distribution (Dcalc = 0.09826 > Dtab;0.95 = 0.01855). Therefore, results obtained with greater homogeneity between diameter growth values within strata tend to provide better estimates because the variations of growth between species are minimized with the group formation, allowing a refinement of estimates when using the results of the stratified parameters. This confirms our formulated hypotheses. The distributions of projected and observed frequencies are presented in Table5
De Liocourt considers that in a balanced forest, the diametric distribution in successive classes (k) is derived from a constant geometric series called “Quotient of De Liocourt” (q), essential parameter for the forest management proposal [20] , in addition to structural evaluations of plant community. In perfect balanced forests q assumes a constant value, indicating a pattern of decreasing exponential distribution in the forest [21] .
The prognosis of the diametric structure, in these circumstances, in addition to estimate with accuracy the forest density, must maintain values equally accurate for obtaining the quotient q, indicating an approximate results for quotients of distribution of frequencies for the forest structure, which can be observed in Table6
In both projected distributions and in the observed one, the q quotients, minimum and maximum, remained in the same classes, k4/k5 and k7/k8 respectively. The lowest accuracy between the projected and observed ratios was found in the estimation without stratification, for the lower and upper diameter classes, reaffirming what was observed in the distribution of frequencies. Generally speaking, disregarding the lower and the upper diameter classes without stratification, there is similarity between the estimated distributions and the observed one, essentially when performed with stratification. Consequently, the prognosis of diametric distribution for the year 2008 resulted more accurate when calculated from stratified data, evaluated by the goodness of fit attested at 95% probability by the application of the Kolmogorov-Smirnoff test in relation to data observed in 2008; the same condition occurred in the evaluation of the Quotient of Liocourt (Figure 3).
Other methodologies can be developed to fit the models of prognosis, providing greater accuracy in their results. In heterogeneous forests, for example, it will be appropriate to separate groups formed by species or botanical families. The application of probability density functions can also improve the prognosis, favoring a distribution with greater similarity between estimated and observed values of the forest.
4. Conclusions
The auto ecological characteristics of each species that composes the plant community favor decisively the formation of groups with different diameter growth and the stratification of diameter growth reduced the variance nine times, enabling the formation of groups statistically different of greater homogeneity.
The stratification of diameter growth approached the predicted results to those observed in the sample population, allowing the forest manager to work with the best estimators in preparation of management proposals.
The methodology of ratio of change, which is based on diameter’s growth and migration of them between
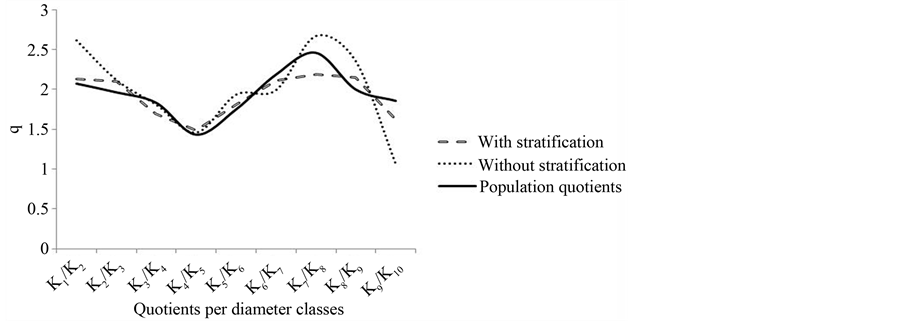
Figure 3. Distribution of De Liocourt quotients for observed and predicted values.
Table 5. Prognosis of the number of individuals per diameter class generated from the values with and without stratification, and observed values of the diametric distribution of Araucaria Forest, for the year 2008.
Table 6. Values for the quotient of De Liocourt from the prognosis of diametric distribution and observed values of Araucaria Forest, for the year 2008.
*Values obtained with all population data.
diameter classes showed to be very efficient to make prognosis in native forests.
The prognosis of diametric distribution for the year 2008 resulted more accurately when calculated from stratified data, evaluated by the goodness of fit attested at 95% probability by the application of the Kolmogorov-Smirnoff test in relation to data observed in 2008.
The evaluation of the coefficient of De Liocourt behaved better in stratification using diameter growth by classes when compared to the results obtained without stratification.
References
- SFB―Serviço Florestal Brasileiro (2010) Florestas do Brasil em resumo―2010: Dados de 2005-2010. SFB, Brasília.
- Vanclay, J.K., Gillicon, A.N. and Keenan, R.J. (1997) Using Functional Attributes to Quantify Site Productivity and Growth Patterns in Mixed Forests. Forest Ecology and Management, 94, 149-163.http://dx.doi.org/10.1016/S0378-1127(96)03972-2
- Sanquetta, C.R., Angelo, H., Brena, D.A. and Mendes, J.B. (1995) Predição da distribuição diamétrica, mortalidade e recrutamento de floresta natural com matriz Markoviana de potência. Floresta, 24, 23-36.
- Péllico Netto, S. and Brena, D.A. (1997) Inventário Florestal. The Authors, Curitiba.
- Scolforo, J.R.S., Pulz, F.A. and Melo, J.M. (1998) Modelagem da produção, idade das florestas nativas, distribuição espacial das espécies e análise estrutural. In: Scolforo, J.R.S., Ed., Manejo Florestal, UFLA/FAEPE, Lavras, 189-206.
- de Souza, D.R., de Souza, A.L., Gama, J.R.V. and Leite, H.G. (2003) Emprego de análise multivariada para estratificação vertical de florestas inequianeas. Revista árvore, 27, 59-63. http://dx.doi.org/10.1590/S0100-67622003000100008
- Ferreira, W.C., Botelho, S.A., Davide, A.C. and Faria, J.M.R. (2007) Avaliação do crescimento do estrato arbóreo de área degrada revegetada à margem do Rio Grande, na usina Hidrelétrica de Camargos, MG. Revista árvore, 31, 177-185. http://dx.doi.org/10.1590/S0100-67622007000100020
- USDA―Soil Survey Staff (1999) Soil Taxonomy―A Basic System of Soil Classification for Making and Interpreting Soil Survey. 2nd Edition, USDA, Washington DC.
- Kaul, P.F.T. (1990) Geologia. IBGE―Instituto Brasileiro de Geografia e Estatística. Região Sul. IBGE, Rio de Janeiro, 29-54.
- Fernandes, A.V. and Backes, A. (1998) Produtividade primária em floresta com Araucaria Angustifolia no Rio Grande do Sul. Iheringia Série Botanica, 51, 63-78.
- Draper, N.R and Smith, E. (1981) Applied Regression Analysis. 2nd Edition, John Wiley & Sons Inc., New York.
- Satterthwaite, F.E. (1946) An Approximate Distribution on Estimates of Variance Components. Biometrics Bulletin, London, 2, 110-114. http://dx.doi.org/10.2307/3002019
- Cochran, W.G. (1963) Sampling Techniques. 2nd Edition, John Wiley & Sons Inc., New York.
- Ebling, A.A., Watzlawick, L.F., Rodrigues, A.L., Longhi, S.J., Longhi, R.V. and Abrão, S.F. (2012) Acuracidade da distribuição diamétrica entre métodos de projeção em Floresta Ombrófila Mista. Ciência Rural, 42, 1020-1026. http://dx.doi.org/10.1590/S0103-84782012000600011
- Figueiredo Filho, A., Dias, A.N., Stepka, T.F. and Sawczuk, A.R. (2010) Crescimento, mortalidade, ingresso e distribuição diamétrica em Floresta Ombrófila Mista. Floresta, 40, 763-776.
- Zanon, M.L.B. and Finger, C.A.G. (2010) Relação de variáveis meteorológicas com crescimento das árvores de Araucaria angustifolia (Bertol.) O. Kuntze em povoamentos implantados. Ciência Florestal, 20, 467-476. http://cascavel.ufsm.br/revistas/ojs-2.2.2/index.php/cienciaflorestal/article/view/2061
- Pulz, F.A., Scolforo, J.R., de Oliveira, A.D., Mello, M.M. and de Oliveira Filho, A.T. (1999) Acuracidade da predição da distribuição diamétrica de uma floresta inequianea com a matriz de transição. Cerne, 5, 1-14.
- Stepka, T.F., Dias, A.N., Figueiredo Filho, A., Machado, S.A. and Sawczuk, A.R. (2012) Modelagem do Incremento em diametro da Araucaria angustifolia em uma Floresta ombrófila Mista no Centro-Sul do Paraná. Floresta, 42, 607-620.
- Meyer, H.A., Reccknagel, A.B., Stevenson, D.D. and Bartoo, R.A. (1961) Forest Management. 2nd Edition, The Ronald Press Company, New York.
- Schneider, P.R. and Finger, C.A.G. (2000) Manejo sustentado de florestas inequianeas heterogêneas. UFSM, Santa Maria.
- Imaña-Encinas, J., Santana, O.A., de Macedo, L.A. and de Paula, J.E. (2008) Distribuição diamétrica de um trecho da Floresta Estacional Semidecidual na área do Ecomuseu do Cerrado. Cerne, 14, 33-45. http://www.redalyc.org/articulo.oa?id=74414105
NOTES
![]()
*Corresponding author.


