Journal of Applied Mathematics and Physics
Vol.2 No.3(2014), Article ID:42745,11 pages DOI:10.4236/jamp.2014.23003
Similarity Reduction of Nonlinear Partial Differential Equations
Amnah S. Al-Johani1,2
1Department of Applied Mathematics, College of Science, Northern Borders University, Arar, Saudi Arabia 2College of Home Economics, Northern Borders University, Arar, Saudi Arabia
Email: xxwhitelinnetxx@hotmail.com
Copyright © 2014 Amnah S. Al-Johani. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Amnah S. Al-Johani. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received December 18, 2013; revised January 15, 2014; accepted January 20, 2014
ABSTRACT
In this work, the HB method is extended to search for similarity reduction of nonlinear partial differential equations. This method is generalized and will apply for a (2 + 1)-dimensional higher order Broer-Kaup System. Some new exact solutions of Broer-Kaup System are found.
Keywords: Similarity Reduction; Exact Solutions; Nonlinear Partial Differential Equations
1. Introduction
In the past few decades, there has been the noticeable progress in the construction of the exact solutions for nonlinear partial differential equations, which has long been a major concern for both mathematicians and physicists. The effort in finding exact solutions to nonlinear differential equation, when they exist, is very important for the understanding of most nonlinear physical phenomena. For instances, the nonlinear wave phenomena observed in fluid dynamics, plasma and optical fibers are often modelled by the bell shaped sech solutions and the kink shaped tanh solutions.
We consider the following a (2 + 1)-dimensional higher order Broer-Kaup system:
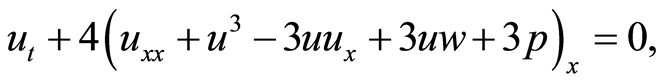 (1)
(1)
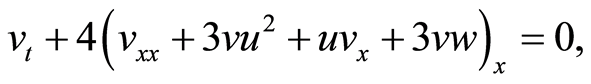 (2)
(2)
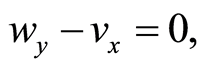 (3)
(3)
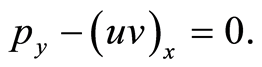 (4)
(4)
which is obtained from the Kadomtsev-Petviashvili (KP) equation by the symmetry constraint [1].
The systems (1)-(4) were given by Li et al [2] solving it via a transformation and tanh-function method to obtain many new exact solutions. Jain et al. [3] reduced a system to a simple (1 + 1)-dimensional nonlinear evolution equation through a simple transformation, and by using the new generally projective Riccati equation expansion method to explore many families of soliton-like and periodic solutions for it. Recently, Li et al. [4] have obtained some new types of multisoliton solutions for the systems (1)-(4) by using some simple transformations as 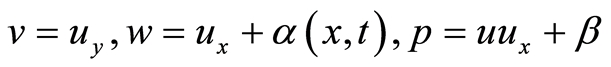 and homogenous balance method.
and homogenous balance method.
The homogenous balance (HB) method is a powerful tool to find solitary wave solutions of nonlinear partial differential equations. Fan et al. [5] presented an improved HB method to obtain more other kinds of exact solutions and introduced a continuation of [5] in [6]. The traditional method for finding similarity reduction of nonlinear partial differential equations is to use classical Lie approach [7,8]. However, the method involves tedious algebraic calculations and still can not be used to find all similarity solutions. Recently,Clarkson and Kruskal devloped a direct and simple method to find more similarity solutions of nonlinear PDEs.
In this work, the HB method is extended to search for similarity reduction of nonlinear partial differential equations. So, more solutions can be obtained by the improved HB method. This method is generalized and can be applied to other nonlinear partial differential equations [9-15].
Similarity Reduction of Nonlinear Partial Differential Equations
We describe the main steps of our method. For a given PDE, say in three variables, say 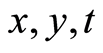
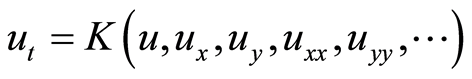 (5)
(5)
we seek its similarity reductions in the form
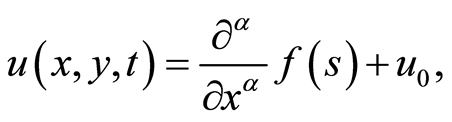 (6)
(6)
where 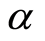 is a constant to determine by balancing between the highest order derivative of the linear terms of
is a constant to determine by balancing between the highest order derivative of the linear terms of  and the nonlinear terms of
and the nonlinear terms of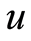 , where
, where  are regarded as undetermined functions.
are regarded as undetermined functions.
Substituting from Equation (6) into Equation (5) and collecting all terms of 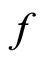 with the same derivative and power. To make the associated equation be an ordinary equations of
with the same derivative and power. To make the associated equation be an ordinary equations of  and
and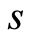 , requiring ratios of their coefficients being functions of
, requiring ratios of their coefficients being functions of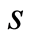 , we obtain a set of determining equations for
, we obtain a set of determining equations for  and other undermined functions, from which
and other undermined functions, from which 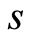 and
and 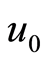 will be obtained.
will be obtained.
To explain this method, we will apply for a (2 + 1)-dimensional higher order Broer-Kaup system (1)-(4), we suppose their similarity solutions are of the form
 (7)
(7)
where
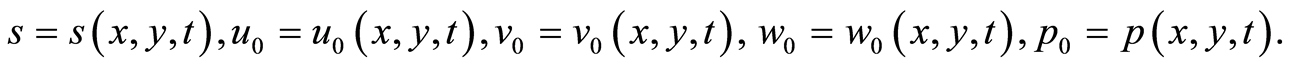
are determined functions. Balancing the highest order of linear term with the nonlinear terms in every equations (1)-(4) to determining  we obtain
we obtain
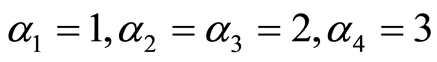 (8)
(8)
the Equation (64) take the following form
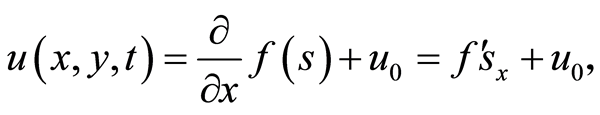 (9)
(9)
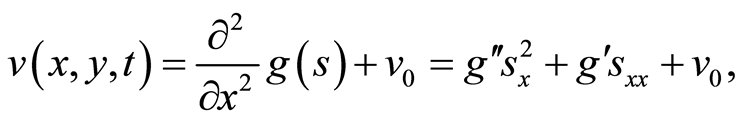 (10)
(10)
 (11)
(11)
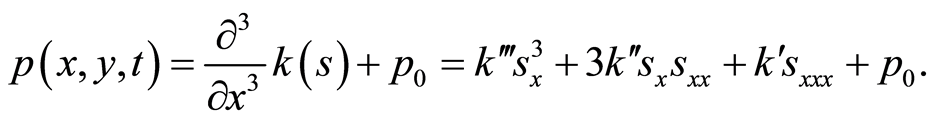 (12)
(12)
Substituting Equations (9)-(12) into the original system (1)-(4) and collecting all terms of 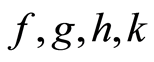 with the same derivative and power leads to
with the same derivative and power leads to
 (13)
(13)
 (14)
(14)
 (15)
(15)
 (16)
(16)
To make Equations (13)-(16) be an ordinary differential equations of  and
and  only for
only for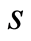 , the ratios of the coefficients of different derivative and power of f,g,h,k must be functions of
, the ratios of the coefficients of different derivative and power of f,g,h,k must be functions of . That is to say, the following constrained conditions are satisfied
. That is to say, the following constrained conditions are satisfied
 (17)
(17)
 (18)
(18)
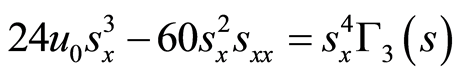 (19)
(19)
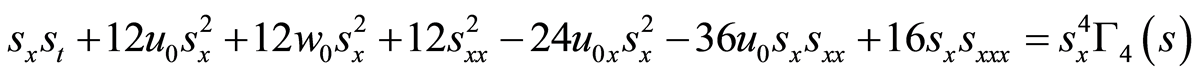 (20)
(20)
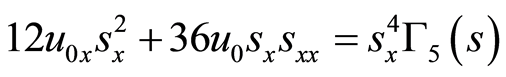 (21)
(21)
 (22)
(22)
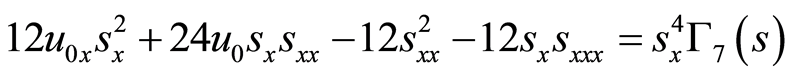 (23)
(23)
 (24)
(24)
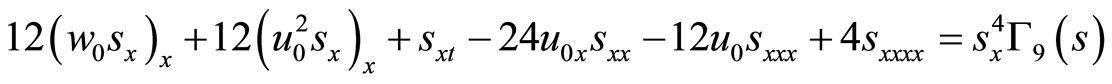 (25)
(25)
 (26)
(26)
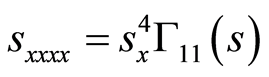 (27)
(27)
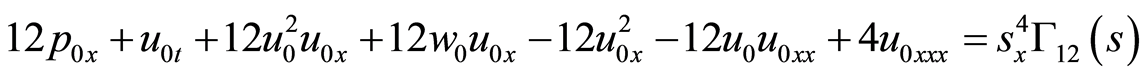 (28)
(28)
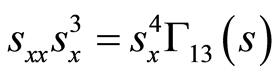 (29)
(29)
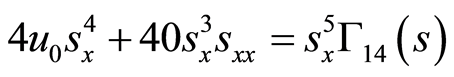 (30)
(30)
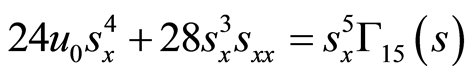 (31)
(31)
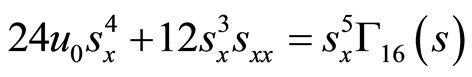 (32)
(32)
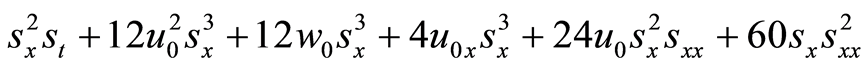 (33)
(33)
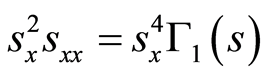 (34)
(34)
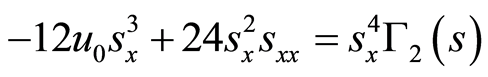 (35)
(35)
 (36)
(36)
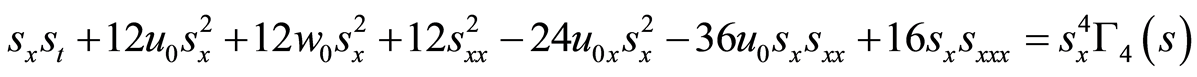 (37)
(37)
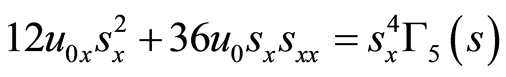 (38)
(38)
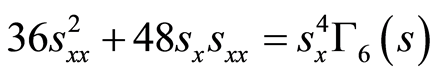 (39)
(39)
 (40)
(40)
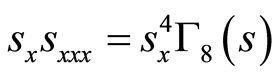 (41)
(41)
 (42)
(42)
 (43)
(43)
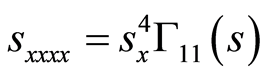 (44)
(44)
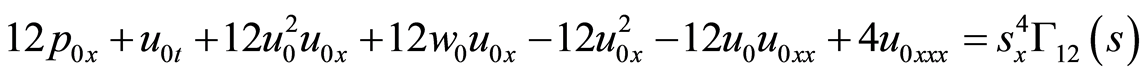 (45)
(45)
 (46)
(46)
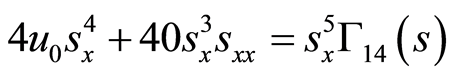 (47)
(47)
 (48)
(48)
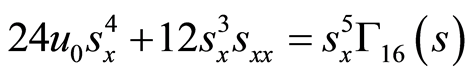 (49)
(49)
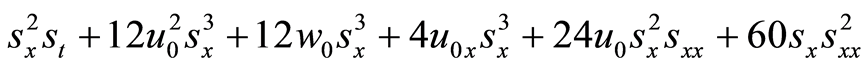 (50)
(50)
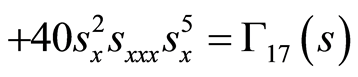 (51)
(51)
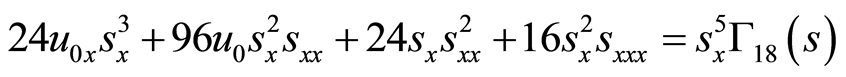 (52)
(52)
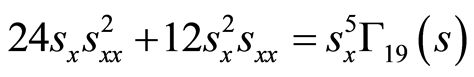 (53)
(53)
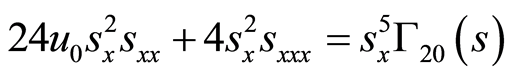 (54)
(54)
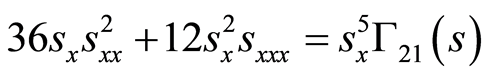 (55)
(55)
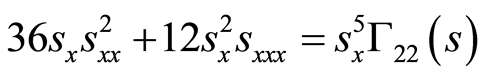 (56)
(56)
 (57)
(57)
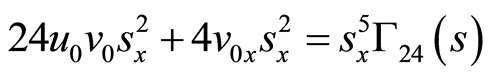 (58)
(58)
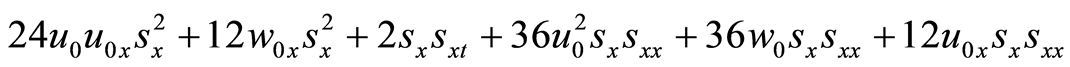 (59)
(59)
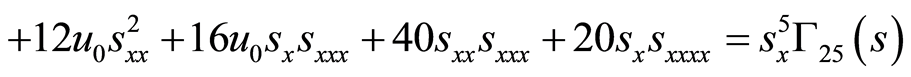 (60)
(60)
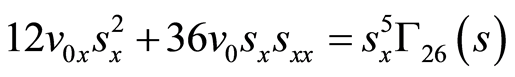 (61)
(61)
 (62)
(62)
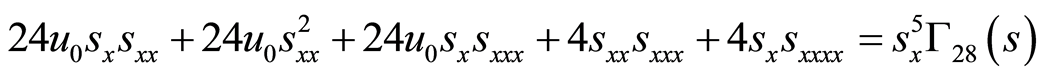 (63)
(63)
 (64)
(64)
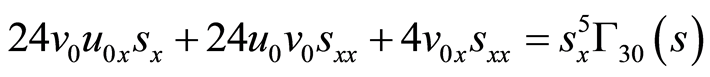 (65)
(65)
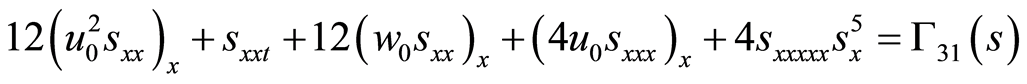 (66)
(66)
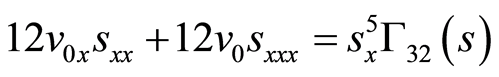 (67)
(67)
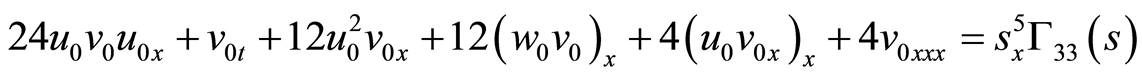 (68)
(68)
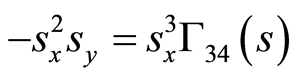 (69)
(69)
 (70)
(70)
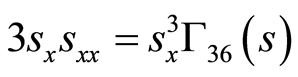 (71)
(71)
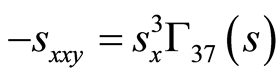 (72)
(72)
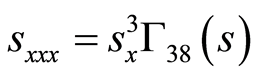 (73)
(73)
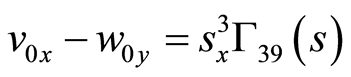 (74)
(74)
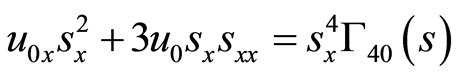 (75)
(75)
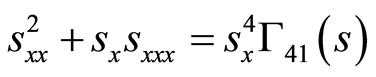 (76)
(76)
 (77)
(77)
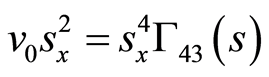 (78)
(78)
 (79)
(79)
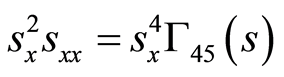 (80)
(80)
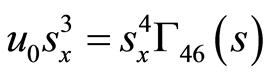 (81)
(81)
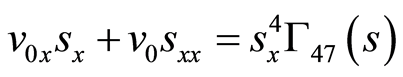 (82)
(82)
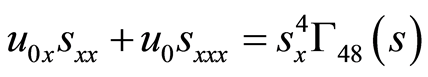 (83)
(83)
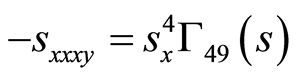 (84)
(84)
 (85)
(85)
where 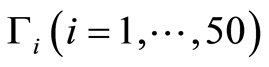 are some arbitrary functions of
are some arbitrary functions of 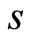 to be determined and take the following form
to be determined and take the following form
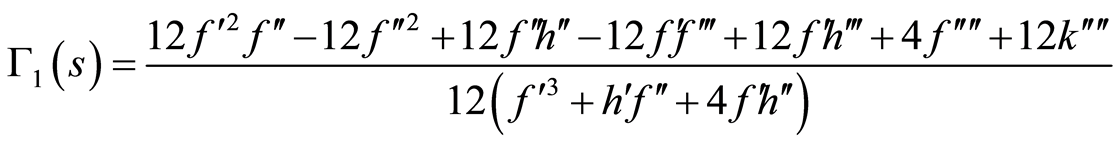
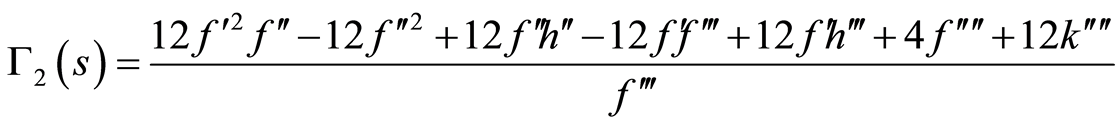
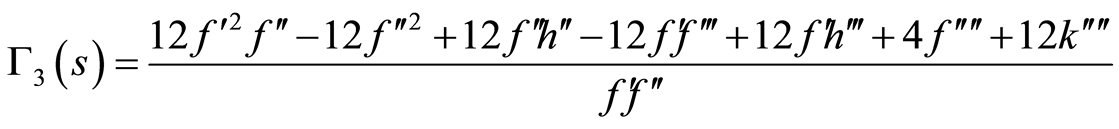

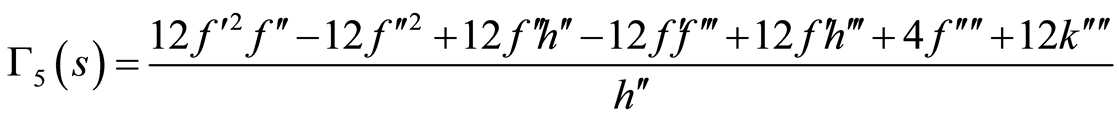
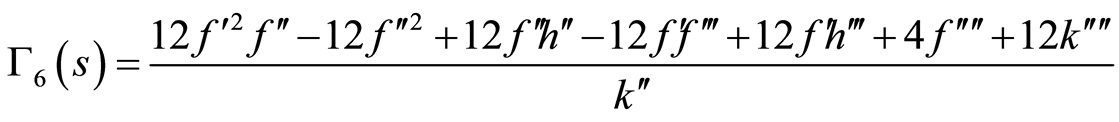
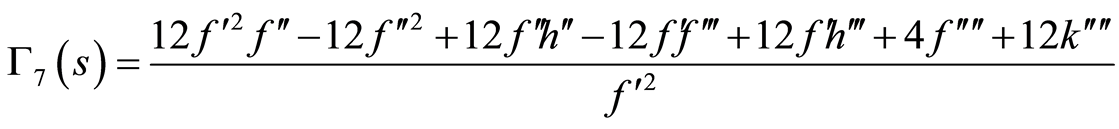
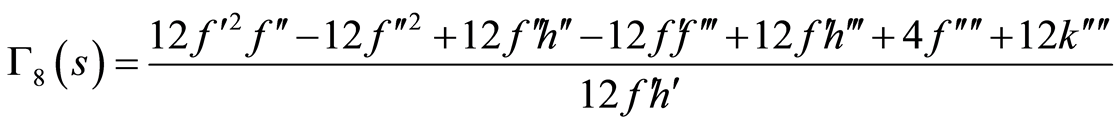
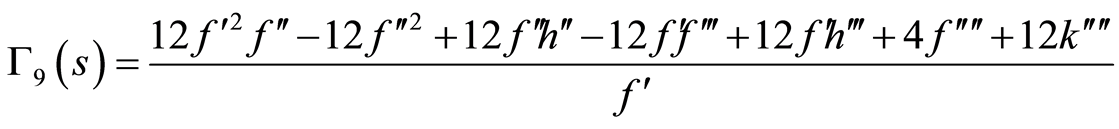
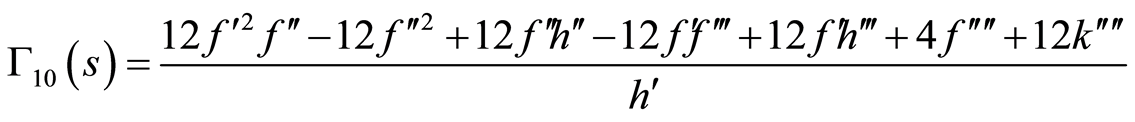

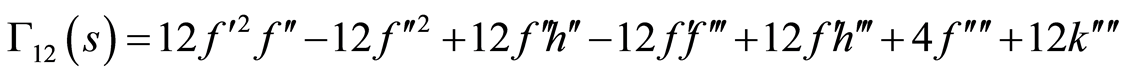
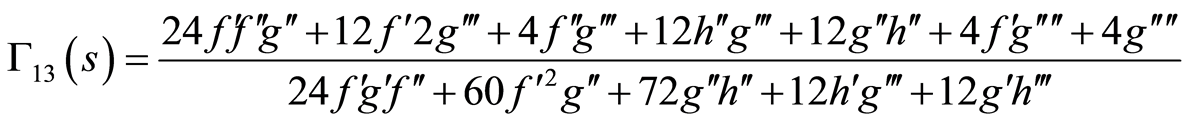
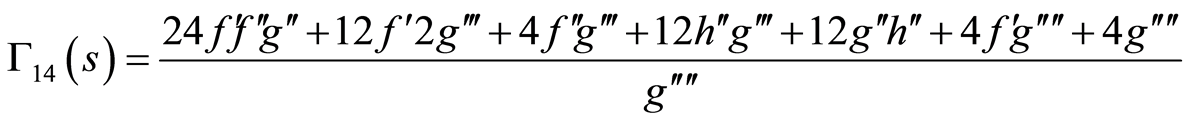
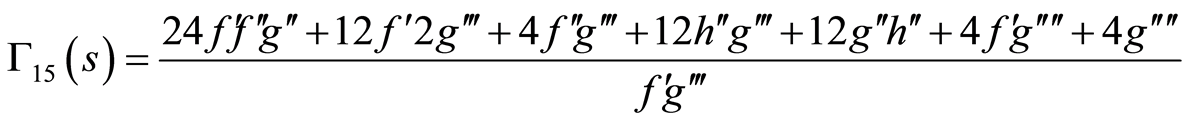
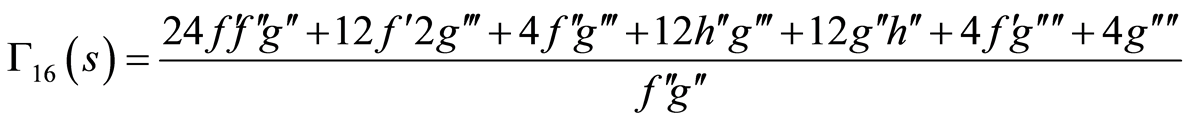
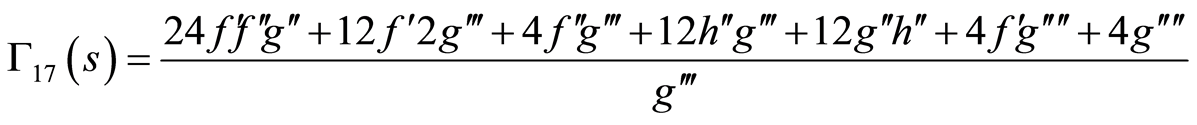

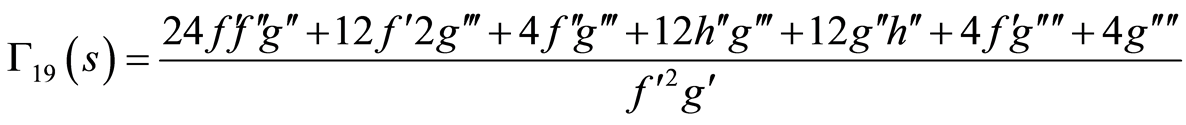
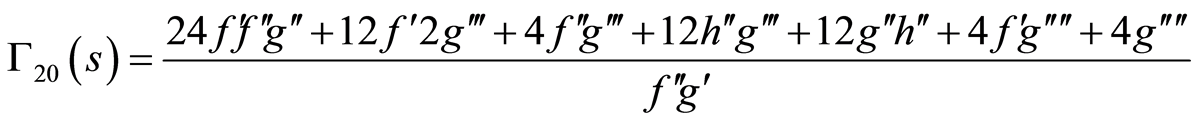
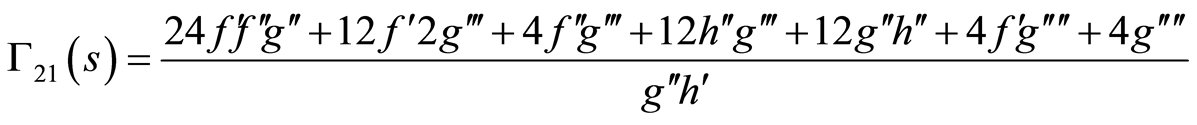
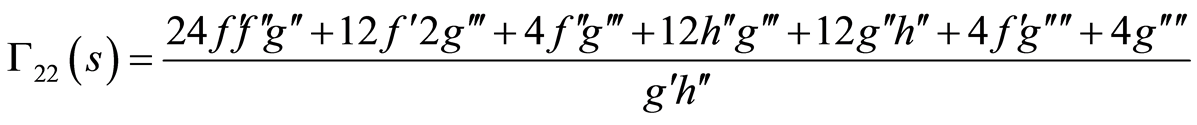
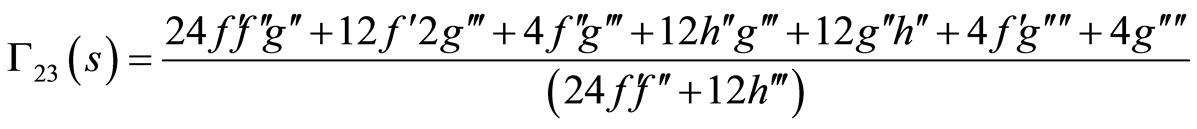
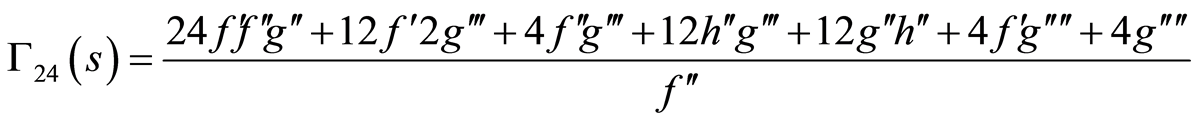

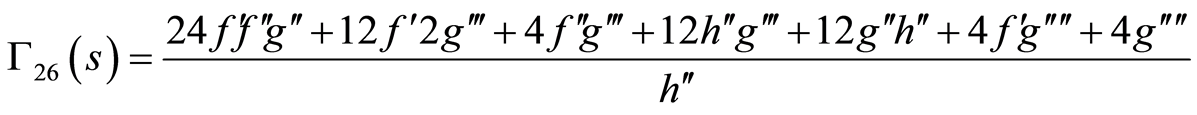
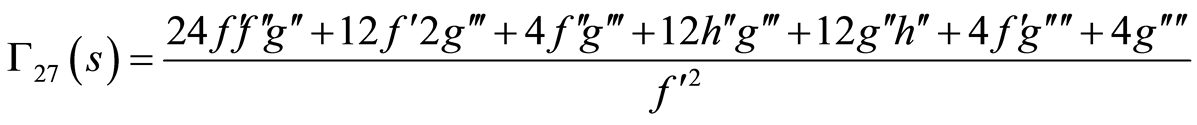
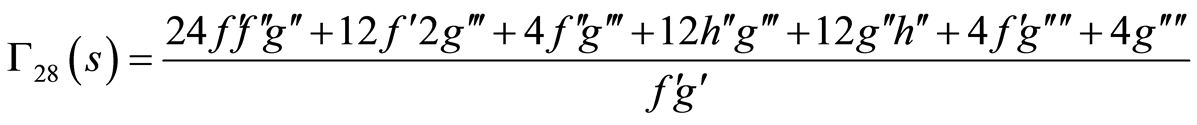
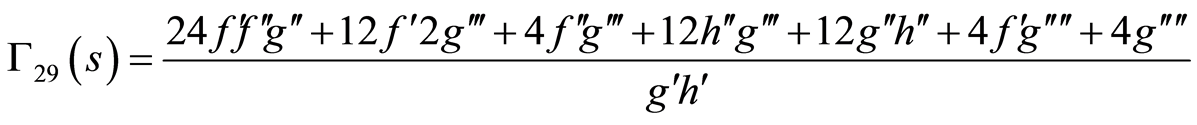
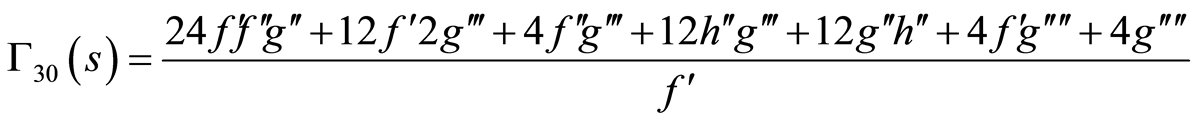
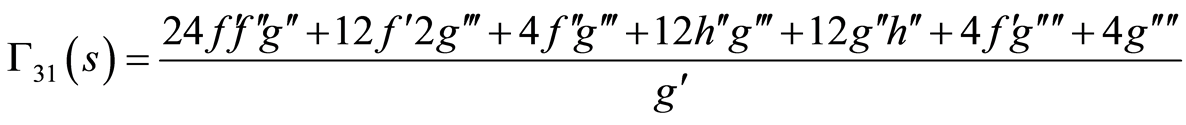
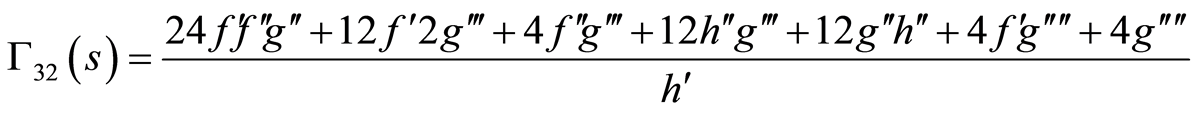

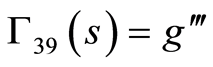
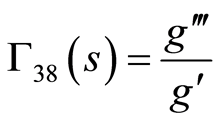

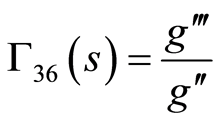
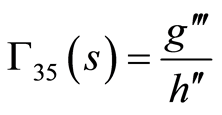
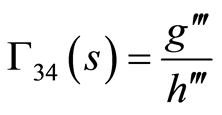
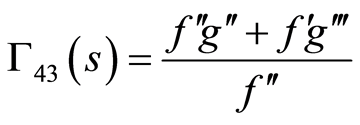
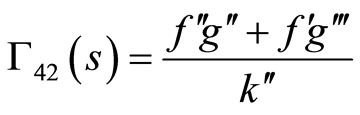
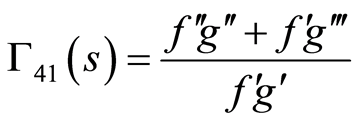
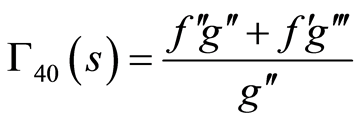

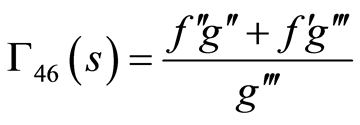
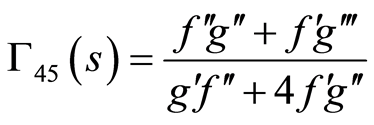

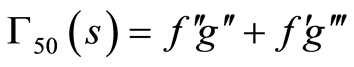

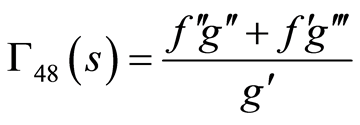 (86)
(86)
There are freedoms in the determination of 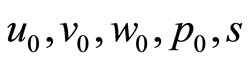 which can exploit the following rules, without loss of generality:
which can exploit the following rules, without loss of generality:
If  has the form
has the form 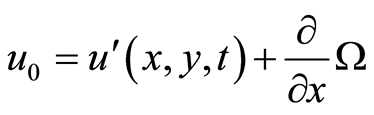 then we can assume that
then we can assume that 
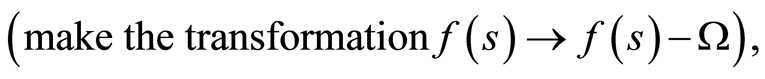
If  has the form
has the form 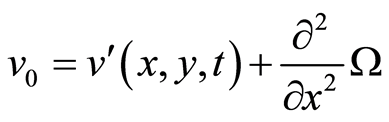 then we can assume that
then we can assume that 
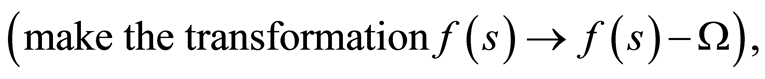
If 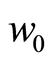 has the form
has the form 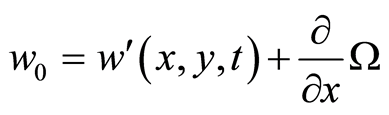 then we can assume that
then we can assume that 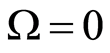
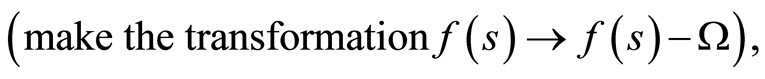
If  has the form
has the form 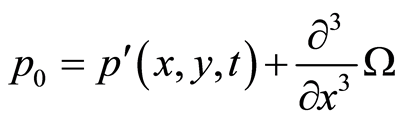 then we can assume that
then we can assume that 

If 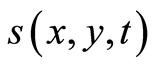 is defined by an equation of the form
is defined by an equation of the form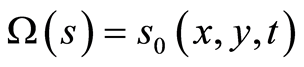 , we can also assume that
, we can also assume that 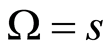 (make the transformation
(make the transformation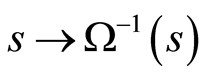 )
)
From Equation (17), we get
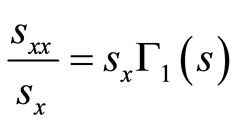 (87)
(87)
integrating Equation (87) with respect to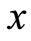 , we get
, we get
 (88)
(88)
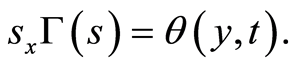 (89)
(89)
integrating Equation (89) with respect to 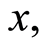 we obtain
we obtain
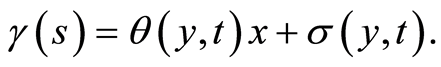 (90)
(90)
By using the rule (e) into Equation (90), we obtain a function 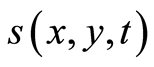 in the form
in the form
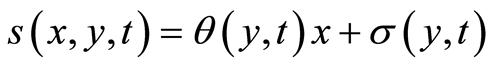 (91)
(91)
substituting from Equation (90) into Equations (17), (20), (24), (25), (26), (53), (54), (55), (56), (63), (64), (71), (72), (73), (76), (77), (80), (83)and (84) we obtain
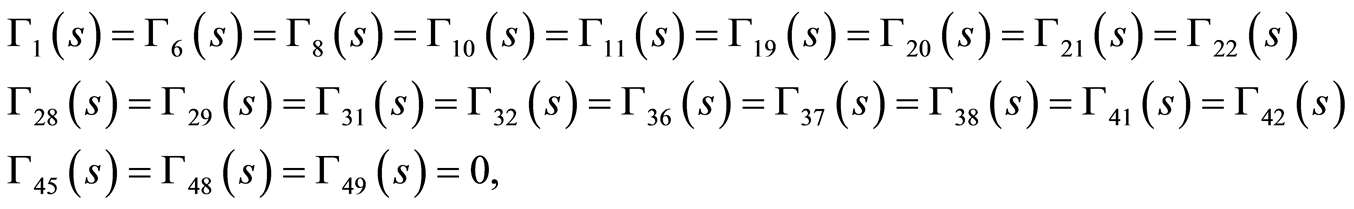 (92)
(92)
where 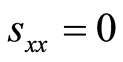 which clear in equation (91)
which clear in equation (91)
By using Equation (91) into Equation (18), we get
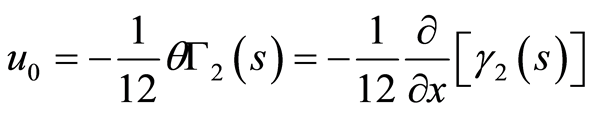 (93)
(93)
where 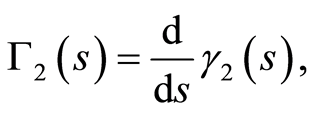
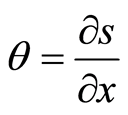 .
.
By apply the rule (a) on Equation (93), we obtain
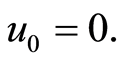
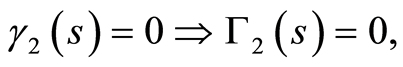 (94)
(94)
substituting from Equations (91), (94) into Equation (20), we obtain
 (95)
(95)
using Equations (91)and (94) into Equation (19), we get
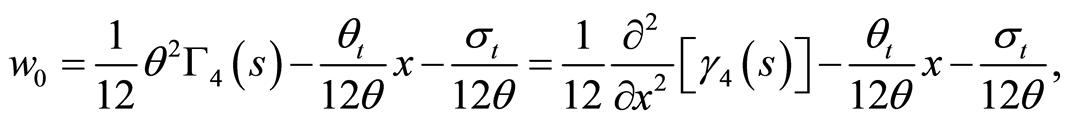 (96)
(96)
where 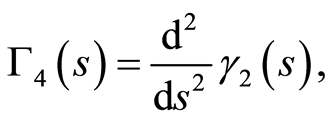
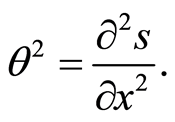
By using the rule (c) into the above equation (96) to become in the form

then Equation (96) take the form
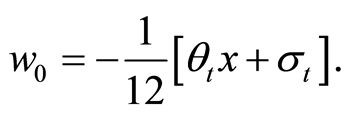 (97)
(97)
substituting from Eqs.( ), (94), (97) into Equations (20), (23), (25), (29), (30), (31), (32), (33)and (34), we obtain
), (94), (97) into Equations (20), (23), (25), (29), (30), (31), (32), (33)and (34), we obtain
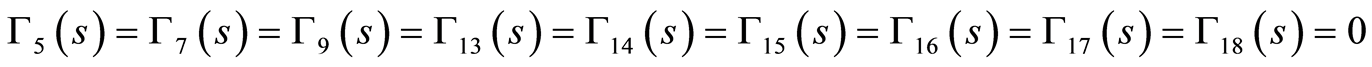 (98)
(98)
from Equation (91) into Equation (57), we get
 (99)
(99)
where 

By using the rule (b) into the above equation (99)
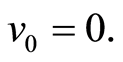
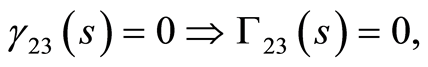 (100)
(100)
substituting from Equations.(91), (94) and (97), into Equations.(61), (62), (65), (68), (75), (78), (81)and (82) then,we obtain
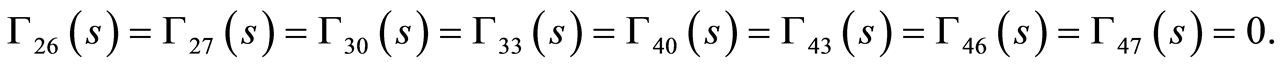 (101)
(101)
Substituting from Equations (91), (94), (97) and (101) into Equations (60), (69), (70), we obtain
 (102)
(102)
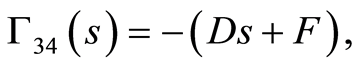 (103)
(103)
 (104)
(104)
where 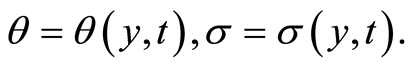
and
 (105)
(105)
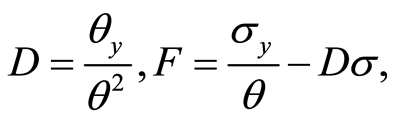 (106)
(106)
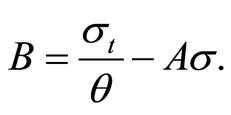 (107)
(107)
Using this notation, the equation (97) take the following form
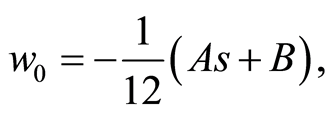 ((108))
((108))
substituting Equations (97) and (100) into Equation (74), we obtain
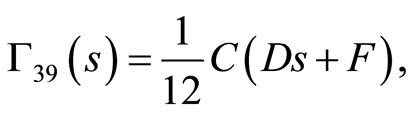 (109)
(109)
using any equation which we need into Equation (28), we obtain
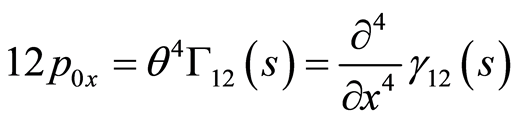 (110)
(110)
where 
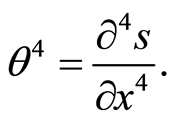
By using the rule (d) after differential with respect to  into Equations (110), we obtain
into Equations (110), we obtain
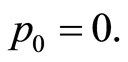
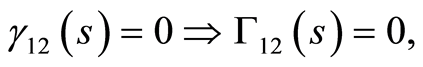 (111)
(111)
Substituting into Equations (9)-(12), we obtain the similarity solutions of the Broer-Kaup system Equations (1)-(4) in the form

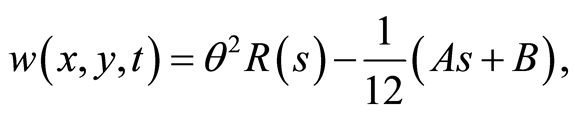

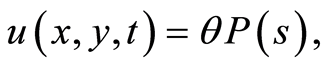 (112)
(112)
where
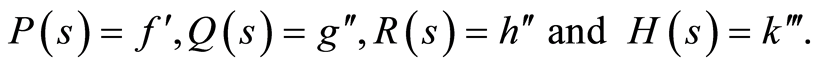 (113)
(113)
with 
Substituting from Equation (112) to obtain an ordinary differential equations from the origin system (1)-(4), we get
 (114)
(114)
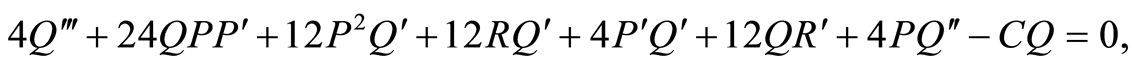 (115)
(115)
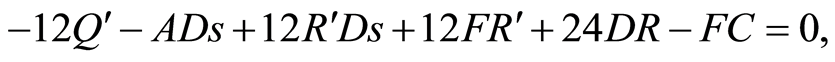 (116)
(116)
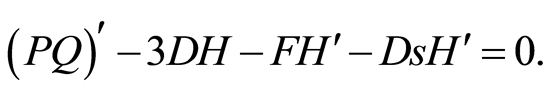 (117)
(117)
where 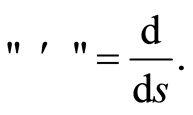
The general solution for the variable 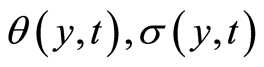 which satisfy Equations (105)-(107) are
which satisfy Equations (105)-(107) are
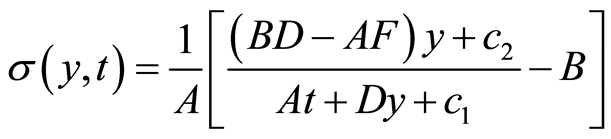
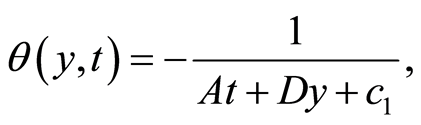 (118)
(118)
where  are arbitrary constants.
are arbitrary constants.
There some subcases for the constants 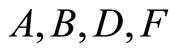
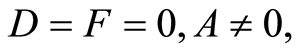 the solutions of Equations (105)-(107) are
the solutions of Equations (105)-(107) are
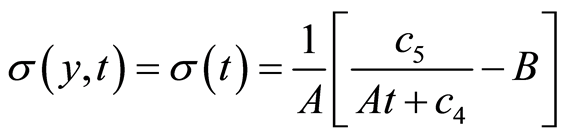
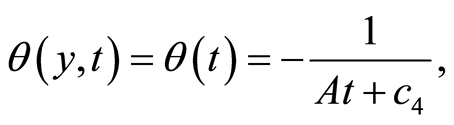 (119)
(119)
where 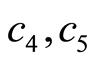 are arbitrary constants. In this case the equations (114)-(117) take the form
are arbitrary constants. In this case the equations (114)-(117) take the form
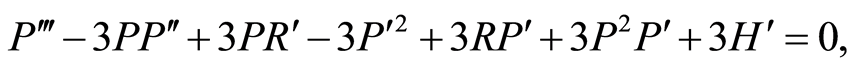 (120)
(120)
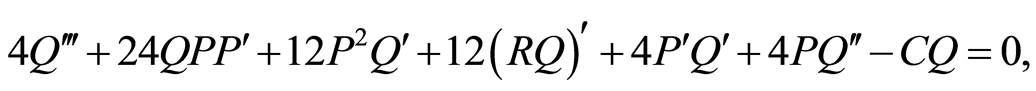 (121)
(121)
 (122)
(122)
 (123)
(123)
the solutions for equations (120)-(123) are
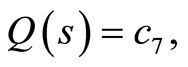
 (124)
(124)

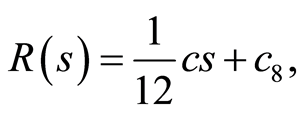
To obtain the solutions for the original system (1)-(4), we substituting from the equations (119), (124) into Equations (112), we get
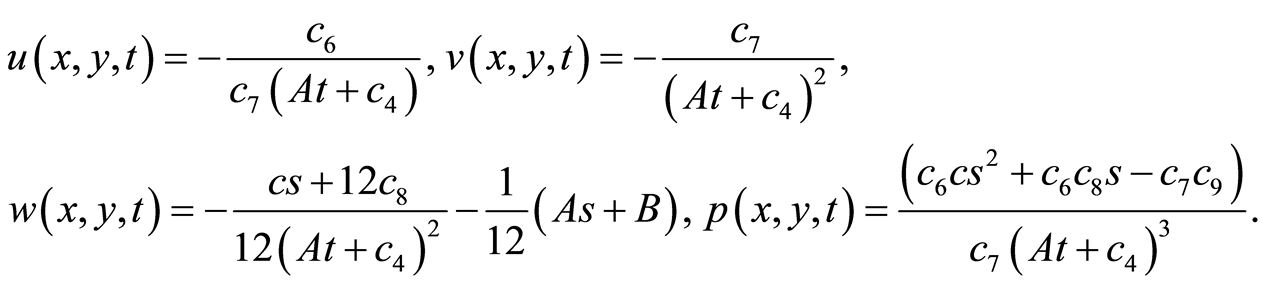 (125)
(125)
REFERENCES
[1] H. A. Zedan, “Exact Solutions for the Generalized KdV Equation by Using Backlund Transformations,” Journal of the Franklin Institute, Vol. 348, No. 8, 2011, pp. 1751-1768. http://dx.doi.org/10.1016/j.jfranklin.2011.04.013
[2] D.-S. Li, et al., “Solving the (2 + 1)-Dimensional Higher Order Broer-Kaup System via a Transformation and Tanh-Function mEthod,” Chaos, Solitons & Fractals, Vol. 20, No. 5, 2004, pp. 1021-1025. http://dx.doi.org/10.1016/j.chaos.2003.09.006
[3] J. Mei, et al., “New Soliton-Like and Periodic Solution of (2 + 1)-Dimensional Higher Order Broer-Kaup System,” Chaos, Solitons & Fractals, Vol. 22, No. 3, 2004, pp. 669-674. http://dx.doi.org/10.1016/j.chaos.2004.02.023
[4] D.-S. Li, et al., “Some New Types of Multisoliton Solutions for the (2 + 1)-Dimensional Higher-Order Broer-Kaup System,” Applied Mathematics and Computation, Vol. 152, No. 3, 2004, pp. 847-853. http://dx.doi.org/10.1016/S0096-3003(03)00601-5
[5] E. G. Fan and H. Q. Zhang, “A Note on the Homogeneous Balance Method,” Physics Letters A, Vol. 246, No. 5, 1998, pp. 403-406.
[6] E. G. Fan, “Two New Applications of the Homogeneous Balance Method,” Physics Letters A, Vol. 265, No. 5-6, 2000, pp. 353-357. http://dx.doi.org/10.1016/S0375-9601(00)00010-4
[7] G. Bluman, “Symmetries and Differential Equations,” Springer-Verlag, New York, 1989. http://dx.doi.org/10.1007/978-1-4757-4307-4
[8] P. J. Olver, “Applications of Lie Group to Differential Equation,” Springer-Verlag, New York, 1986. http://dx.doi.org/10.1007/978-1-4684-0274-2
[9] P. A. Clarkson, “New Similarity Solutions for the Modified Boussinesq Equation,” Journal of Physics A: Mathematical and General, Vol. 22, No. 13, 1989, pp. 2355-2365. http://dx.doi.org/10.1088/0305-4470/22/13/029
[10] Y. Yu, Q. Wang and H. Q. Zhang, “The Extended Jacobi Elliptic Function Method to Solve a Generalized Hirota-Satsuma Coupled KdV Equations,” Chaos, Solitons & Fractals, Vol. 26, No. 5, 2005, pp. 1415-1421. http://dx.doi.org/10.1016/j.chaos.2005.04.011
[11] J. L. Zhang, M. L. Wang, Y. M. Wang, Z. D. Fang, “The Improved F-Expansion Method and Its Applications,” Physics Letters A, Vol. 350, No. 1-2, 2006, pp. 103-109. http://dx.doi.org/10.1016/j.physleta.2005.10.099
[12] E. M. E. Zayed and H. Zedan, “On the Solitary Wave Solutions for Nonlinear Hirota-Satsuma Coupled KdV of Equations,” Chaos, Solitons & Fractals, Vol. 22, No. 2, 2004, pp. 285-303. http://dx.doi.org/10.1016/j.chaos.2003.12.045
[13] A. M. Wadati, “Introduction to Solitons,” Pramana: Journal of Physics, Vol. 57, No. 5-6, 2001, pp. 841-847.
[14] Z. Chen, D. H. Zhao and J. Ruan, “Dynamic Analysis of High-Order Cohen-Grossberg Neural Networks with Time Delay,” Chaos, Solitons & Fractals, Vol. 32, No. 4, 2007, pp. 1538-1546. http://dx.doi.org/10.1016/j.chaos.2005.11.095
[15] Hassan A. Zedan, “Solution of (3 + 1) - Dimensional Nonlinear Cubic Schrodinger Equation by Differential Transform Method,” Mathematical Problems in Engineering, Vol. 2012, 2012, 14 p.
NOTES

*Corresponding author.

