International Journal of Intelligence Science
Vol.09 No.01(2019), Article ID:90261,15 pages
10.4236/ijis.2019.91003
Solving Intuitionistic Fuzzy Linear Programming Problem
Arpita Kabiraj1, Prasun Kumar Nayak2, Swapan Raha1
1Department of Mathematics, Siksha Bhavana (Institute of Sciences), Santiniketan, India
2Department of Mathematics, Midnapore College (Autonomous), Midnapore, India
Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 18, 2018; Accepted: January 26, 2019; Published: January 29, 2019
ABSTRACT
Intuitionistic Fuzzy Set (IFS) can be used as a general tool for modeling problems of decision making under uncertainty where, the degree of rejection is defined simultaneously with the degree of acceptance of a piece of information in such a way that these degrees are not complement to each other. Accordingly, an attempt is made to solve intuitionistic fuzzy linear programming problems using a technique based on an earlier technique proposed by Zimmermann to solve fuzzy linear programming problem. Our proposed technique does not require the existing ranking of intuitionistic fuzzy numbers. This method is also different from the existing weight assignment method or the Angelov’s method. A comparative study is undertaken and interesting results have been presented.
Keywords:
Intuitionistic Fuzzy Set, Intuitionistic Index, Intuitionistic Fuzzy Number, Intuitionistic Fuzzy Linear Programming Problem, Fuzzy Linear Programming Problem

1. Introduction
Optimization problems exhibit some level of imprecisions and vagueness. Such phenomena have been well-captured through fuzzy sets in modeling these problems. Applications of fuzzy set theory in optimization of decisions have been studied extensively ever since the introduction of fuzzy sets. The theory of fuzzy sets proposed by Zadeh is a realistic and practical means to describe the objective world that we live in and has also been successfully applied in various other fields.
In decision making problems, the concept of maximizing decision under uncertainty was proposed by Bellman and Zadeh [1] . This concept was adopted to problems of mathematical programming by Tanaka and others. Zimmermann [2] presented a fuzzy approach to multi-objective linear programming problems. He also studied the duality relations in fuzzy linear programming. Fuzzy linear programming problem (FLPP) with fuzzy coefficients was formulated by Negoita [3] and called robust programming. Dubois and Prade investigated linear fuzzy constraints [4] . Tanaka and Asai also proposed a formulation of fuzzy linear programming with fuzzy constraints and suggested a method for its solution which is based on inequality relation between fuzzy numbers [5] . This ranking of fuzzy numbers is an important issue in the study of optimization using fuzzy set theory.
Recent years have witnessed a growing interest in the study of decision making problems under uncertainty with intuitionistic fuzzy sets/numbers [6] [7] [8] [9] [10] . Out of several higher order fuzzy sets, intuitionistic fuzzy set introduced by Atanassov [11] [12] [13] [14] has been found to be highly useful in dealing with imprecision. Since this fuzzy set generalization can present the degrees of membership and non-membership of an element of the set with a degree of hesitancy, the knowledge and semantic representation becomes more meaningful and applicable. Authors in [15] presented an overview on IFS viz., some definitions, basic operations, some algebra, modal operators and also its normalization. Later, D. Dubey [16] proposed an approach based on value and ambiguity indices to solve LPPs with data as Triangular Intuitionistic Fuzzy Numbers. Parvathi and Malathi [17] [18] worked on the intuitionistic fuzzy decisive set method which, is a combination of bisection method and phase one of the simplex method to obtain a feasible solution. In [19] , the authors described a method to approximate a TIFN to a nearly approximated interval number. The average ranking index is also introduced here to find out order relations between two TIFNs. On ranking intuitionistic fuzzy numbers, some work had been reported in the literature. Mitchell [20] considered the problem of ranking a set of intuitionistic fuzzy numbers to define a fuzzy rank and a characteristic vagueness factor for each intuitionistic fuzzy number. Ranking using score function is introduced in [21] . Here, all the arithmetic operations of TIFN are based on -cut method. Ranking of intuitionistic fuzzy number with expected interval is introduced in [22] . A. N. Gani, S. Abbas [23] worked on a new average method for finding an optimal solution for an intuitionistic fuzzy transportation problem. The main feature of this method is that it requires very simple arithmetical calculations and avoids large number of iterations. An accuracy function to defuzzify TIFN is also used here. The concept of an intuitionistic fuzzy set is a generalization of the concept of a fuzzy set.
Angelov [24] proposed optimization in an intuitionistic fuzzy environment. Hussain and Kumar [25] [26] [27] and Nagoor Gani and Abbas [23] proposed a method for solving intuitionistic fuzzy transportation problem. Ye [28] discussed expected value method for intuitionistic trapezoidal fuzzy multicriteria decision-making problems. Wan and Dong [29] used possibility degree method for interval-valued intuitionistic fuzzy numbers for decision making.
In this paper, our aim is to propose a method to solve intuitionistic fuzzy linear programming problem (IFLPP) using a technique based on an earlier technique proposed by Zimmermann [2] for solving fuzzy linear programming problems. First, we represent such an uncertain optimization problem in the form of a LPP where each of the coefficients of the objective and the constraints are considered as IFS’s and the inequalities as intuitionistic fuzzy inequalities. These IFS’s are first defuzzified based on maximum membership and is translated into a LPP with crisp coefficients and intuitionistic inequalities. Next, the reduced IFO problem is restructured according to Bellman and Zadeh to an ordinary LPP where decisions are based on maximum membership and minimum non-membership. This technique does not require the existing ranking of intuitionistic fuzzy numbers. This method is also different from the Weight assignment method, Angelov’s method as well as the modified subgradient method to solve IFLPP using FLPP technique. A comparative study is performed and interesting results are presented.
The paper is organized in six sections. The introductory section is followed by presentation of some basic concepts necessary for the development of a mechanism for solving intuitionistic fuzzy linear programming problems. In this section, basic concept of Triangular Intuitionistic Fuzzy Number (TIFN) is described. In Section 3, we discuss fuzzy linear programming problem and introduce a new method analogous with it, to solve IFLPP when both the coefficient matrix of the constraints and cost coefficients are intuitionistic fuzzy in nature. In Section 4, there is a comparative study between some of the other optimization techniques with our proposed technique for solving an intuitionistic fuzzy linear programming problem. Section 5 concludes the present paper and refers to some problems for further studies which is followed by a list of references in the last section.
2. Preliminaries
Definition 1 [19] Let be a finite universal set. An Intuitionistic fuzzy set (IFS) in a given universal set U is an object having the form
where the functions and respectively define the degree of membership and the degree of non-membership of an element , such that they satisfy the following conditions:
known as intuitionistic condition. The degree of acceptance and of non-acceptance can be arbitrary.
Definition 2 [17] For all , let , which is called the Atanassov’s intuitionistic index of the element in the set or the degree of uncertainty or the indeterministic part of or a measure of hesitation. Obviously, ; . When , i.e., , becomes a fuzzy set. Therefore, a fuzzy set is a special Intuitionistic Fuzzy Set (IFS).
Definition 3 [15] Let and be two Atanassov’s IFSs defined on U. if and only if and ; for any .
Definition 4 [15] Let and be two Atanassov’s IFSs defined on U. if and only if and ; for all .
Definition 5 [19] An intuitionistic fuzzy set A of U is said to be normal if such that , (so ).
Definition 6 [19] A subset -cut of U, generated by IFS , where are fixed numbers such that is defined as
Thus, the -cut of an intuitionistic fuzzy set to be denoted by , is defined as the crisp set of elements x which belong to at least to the degree and which does not belong to at most to the degree .
Definition 7 [19] An intuitionistic fuzzy number (IFN) is
1) an intuitionistic fuzzy subset of the real line ;
2) normal, i.e., such that , (so );
3) convex for the membership function, i.e.,
4) concave for the non-membership function, i.e.,
Definition 8 [19] A triangular intuitionistic fuzzy number (TIFN) is a special IFS on the real number set , whose membership function and non-membership functions are defined as follows:
(1)
and
(2)
where l, r are called spreads and a is called mean value. and represent the maximum degree of membership and minimum degree of non-membership respectively such that they satisfy the condition
Note 1.: From the above definitions we see that the numbers and reflect respectively the extent of a degree of acceptance and that of rejection of an element x to the set , and the number is the extent of indeterminacy.
3. Intuitionistic Fuzzy Programming Technique
We consider the linear programming problem (LPP) with cost of decision variables and co-efficient matrix of constraints represented as trapezoidal fuzzy in nature:
subject to
where,
(3)
(4)
(5)
The class of fuzzy linear programming models is not uniquely defined as it depends upon the type of fuzziness as also its specification as prescribed by the decision maker. Accordingly, the class of FLPP can be broadly classified as:
1) LPP with fuzzy inequalities and crisp objective function,
2) LPP with crisp inequalities and fuzzy objective function,
3) LPP with fuzzy inequalities and fuzzy objective function,
4) LPP with fuzzy resources and fuzzy coefficients, also termed as LPP with fuzzy parameters, i.e., elements of are fuzzy numbers.
Intuitionistic fuzzy optimization (IFO), a method of uncertainty optimization, is put forward on the basis of intuitionistic fuzzy sets, due to Atanassov [11] . It is an extension of fuzzy optimization in which the degrees of rejection of objective(s) and constraints are considered together with the degrees of satisfaction. According to different interpretations, distinct IFLPP could be formulated.
In this paper, we try to examine the case in which all the co-efficients and the right hand side constants appearing in the constraints are modeled as TIFN and then reformulated as a LPP with intuitionistic fuzzy inequalities and objective function.
subject to
where,
As co-efficients are TIFN so maximum membership occurs at and , hence the above given problem is reformulated as
subject to
where the inequality relations are considered as intuitionistic fuzzy inequalities.
For the objective function, the intuitionistic fuzzifier max is understood in the sense of the satisfaction of the aspiration level
as best as possible. To solve this we first choose an appropriate membership and non-membership function for each of the intuitionistic fuzzy inequality. In particular,
and
denote respectively the membership and non-membership functions for the objective function and
respectively denote the membership and non-membership function for the jth constraint. Let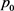 , and
, and 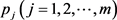 be the permissible tolerances for the objective function and the jth constraint. Then, we decide
be the permissible tolerances for the objective function and the jth constraint. Then, we decide 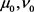 and
and 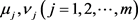 to be non-decreasing and continuous linear membership and non-membership functions as per the choice given below:
to be non-decreasing and continuous linear membership and non-membership functions as per the choice given below:
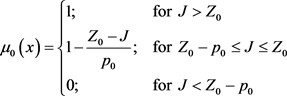 (6)
(6)
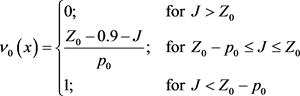 (7)
(7)
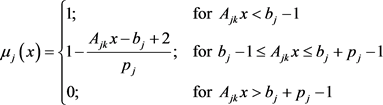 (8)
(8)
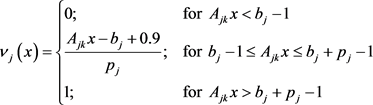 (9)
(9)
This leads to the following equivalent crisp LPP:
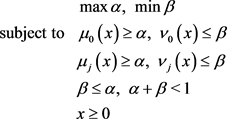 (10)
(10)
where 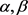 denotes respectively the minimal acceptance degree and the maximal degree of rejection, which, in turn, implies that
denotes respectively the minimal acceptance degree and the maximal degree of rejection, which, in turn, implies that
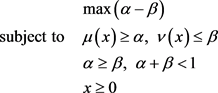 (11)
(11)
Now, the above can be solved easily by using usual simplex method.
Thus, the following are the steps proposed to solve the LPP under the intuitionistic fuzzy environment
Algorithm:
Input: An Intuitionistic fuzzy LPP in mathematical form.
Output: Optimal solution and corresponding decision.
Step 1: Choose an aspiration level 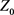 of the objective function and set tolerances for objective as well as constraints so that required solution become feasible.
of the objective function and set tolerances for objective as well as constraints so that required solution become feasible.
Step 2: Defuzzify the intuitionistic fuzzy sets appearing as co-efficients in the objective and the constraints and subsequently rewrite the system with crisp numbers and intuitionistic inequalities.
Step 3: Construct membership function 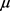 and non-membership function
and non-membership function  for the objective and the constraints depending on the choice of
for the objective and the constraints depending on the choice of 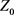 and tolerances as set.
and tolerances as set.
Step 4: Taking minimal acceptance degree 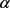 and maximal degree of rejection
and maximal degree of rejection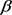 , formulate the following equivalent ordinary Linear programming problem:
, formulate the following equivalent ordinary Linear programming problem:
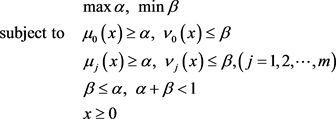 (12)
(12)
where


Step 5: Accordingly, the above formulation is equivalent to:

Step 6: Solve the ordinary linear programming problem using simplex technique.
Example 1: Let us consider an intuitionistic fuzzy LPP as in the following:

System (14) is defuzzified into the crisp model as,

where 
According to Zimmermann’s approach for a symmetric model, we assume that


are as given below:






Following Zimmermann’s approach to solve (14), we need to solve the following crisp LPP:

where 


Accordingly, we have the formulation:

Now, by using simplex algorithm, we solve the above problem and obtain the solution as




For different values of 
Table 1. Solution for different 
4. An Illustrative Study
In Section 3, instead of IFLPP if we take the corresponding FLPP and solve the same using Zimmermann’s technique [2] [30] [31] [32] [33] [34] , Weight assignment method [35] and Angelov’s method [24] [36] [37] for the previous example and some of the other problems then, a comparative study can be performed for a better understanding of the utility of the proposed method.
Problem 1:

Problem 2:

Problem 3:

Result and discussion: Table 1 lists the solution of (14) for different values of 




In fact, there are some cases where due to insufficiency in the available information, the evaluation of the membership and non-membership functions together gives better and/or satisfactory result than considering either the membership value or the non-membership value. Accordingly, there remains a part indeterministic on which hesitation survives. Certainly fuzzy optimization is unable to deal such hesitation since in this case here membership and non-membership functions are complement to each other. Here, we extend Zimmermann’s optimization technique for solving FLPP. In our proposed technique, sum of membership degree and non-membership degree always taken as strictly less than one and hence hesitation arises. Consequently, to achieve the aspiration level 


5. Conclusions
In human decision making problem, IFO plays an important and useful role. This approach converts the introduced intuitionistic fuzzy optimization (IFO) problem into a crisp (non-fuzzy) LPP. The advantage of the IFO problem is two-fold: they give a rich apparatus for formulation of optimization problems and, on the other hand, the solution of IFO problems can satisfy the objective(s) with a greater degree than the analogous fuzzy optimization problem.
Figure 1. For Problem 1 the value of J with our proposed approach.
Figure 2. For Problem 1 the value of J with Zimmermann’s approach.
Table 2. Optimal solution using different techniques for Problem 1.
Table 3. Optimal solution using different techniques for Problem 2.
Table 4. Optimal solution using different techniques for Problem 3.
There is considerable scope for research in this domain. In future, this research work could be extended to some other uncertain environment such as representation using Pythagorean fuzzy set [38] , interval neutrosophic set [39] etc. This also includes, in particular, an attempt to find solution for a class of IFLPP without converting them to crisp LPP and to compare other existing fuzzy optimization techniques with the proposed one.
Acknowledgements
This research is supported by UGC SAP-DRS Phase-III programme at the Department of Mathematics. UGC’s financial support is highly appreciated.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Kabiraj, A., Nayak, P.K. and Raha, S. (2019) Solving Intuitionistic Fuzzy Linear Programming Problem. International Journal of Intelligence Science, 9, 44-58. https://doi.org/10.4236/ijis.2019.91003
References
- 1. Bellman, R.E. and Zadeh, L.A. (1970) Decision Making in a Fuzzy Environment. Management Science, 17, 141-164. https://doi.org/10.1287/mnsc.17.4.B141
- 2. Bector, C.R. and Chandra, S. (2005) Fuzzy Mathematical Programming and Fuzzy Matrix Games. In: Studies in Fuzziness and Soft Computing, Volume 169, Springer-Verlag, Berlin Heidelberg, 57-94.
- 3. Negoita, C.V. (1981) The Current Interest in Fuzzy Optimization. Fuzzy Sets and Systems, 6, 261-269. https://doi.org/10.1016/0165-0114(81)90004-X
- 4. Dubois, D. and Prade, H. (1980) Systems of Linear Fuzzy Constraints. Fuzzy Sets and Systems, 3, 37-48. https://doi.org/10.1016/0165-0114(80)90004-4
- 5. Tanaka, H. and Asai, K. (1984) Fuzzy Linear Programming Problems with Fuzzy Numbers. Fuzzy Sets and Systems, 13, 1-10. https://doi.org/10.1016/0165-0114(84)90022-8
- 6. Garg, H. (2013) An Approach for analyzing Fuzzy System Reliability Using Particle Swarm Optimization and Intuitionistic Fuzzy Set Theory. Journal of Multiple-Valued Logic and Soft Computing, 21, 335-354.
- 7. Garg, H., Rani, M., Sharma, S.P. and Vishwakarma, Y. (2014) Bi-Objective Optimization of the Reliability-Redundancy Allocation Problem for Series-Parallel System. Journal of Manufacturing Systems, 33, 353-367. https://doi.org/10.1016/j.jmsy.2014.02.008
- 8. Garg, H., Rani, M., Sharma, S.P. and Vishwakarma, Y. (2014) Intuitionistic Fuzzy Optimization Technique for Solving Multi-Objective Reliability Optimization Problems in Interval Environment. Expert Systems with Applications, 41, 3157-3167. https://doi.org/10.1016/j.eswa.2013.11.014
- 9. Garg, H. (2016) A Novel Approach for Analyzing the Reliability of Series-Parallel System Using Credibility Theory and Different Types Of Intuitionistic Fuzzy Numbers. Journal of Brazilian Society of Mechanical Sciences and Engineering, 38, 1021-1035. https://doi.org/10.1007/s40430-014-0284-2
- 10. Garg, H. (2018) Some Arithmetic Operations on the Generalized Sigmoidal Fuzzy Numbers and Its Application. Granular Computing, 3, 9-25. https://doi.org/10.1007/s41066-017-0052-7
- 11. Atanassov, K. (1986) Intuitionistic Fuzzy Sets. Fuzzy Sets and Systems, 20, 87-96. https://doi.org/10.1016/S0165-0114(86)80034-3
- 12. Atanassov, K. (1995) Ideas for Intuitionistic Fuzzy Sets Equations, Inequations and Optimization. Notes on Intuitionistic Fuzzy Sets, 1, 17-24.
- 13. Atanassov, K. (1999) Intuitionistic Fuzzy Sets: Theory and Applications. Physica-Verlag, Berlin Heidelberg, 1-137. https://doi.org/10.1007/978-3-7908-1870-3
- 14. Atanassov, K. (1994) New Operations Defined over the Intuitionistic Fuzzy Sets. Fuzzy Sets and Systems, 61, 137-142. https://doi.org/10.1016/0165-0114(94)90229-1
- 15. Ejegwa, P.A., Akowe, S.O., Otene, P.M. and Ikyule, J.M. (2014) An Overview on Intuitionistic Fuzzy Sets. International Journal of Scientific & Technology Research, 3, 142-145.
- 16. Dubey, D. and Mehra, A. (2011) Linear Programming with Triangular Intuitionistic Fuzzy Number. European Society for Fuzzy Logic and Technology, 563-569. https://doi.org/10.2991/eusflat.2011.78
- 17. Parvathi, R. and Malathi, C. (2012) Intuitionistic Fuzzy Linear Optimization. Notes on Intuitionistic Fuzzy Sets, 18, 48-56.
- 18. Parvathi, R. and Malathi, C. (2012) Intuitionistic Fuzzy Linear Programming Problem. World Applied Sciences Journal, 17, 1802-1807.
- 19. Seikh, M.R., Nayak, P.K. and Pal, M. (2013) Notes on Triangular Intuitionistic Fuzzy Numbers. International Journal of Mathematics in Operational Research, 5, 446-465. https://doi.org/10.1504/IJMOR.2013.054730
- 20. Mitchell, H.B. (2004) Ranking Intuitionistic Fuzzy Numbers. International Journal of Uncertainity, Fuzziness and Knowledge-Based Systems, 12, 377-386. https://doi.org/10.1142/S0218488504002886
- 21. Nagoorgani, A. and Ponnalagu, K. (2013) An Approach to Solve Intuitionistic Fuzzy Linear Programming Problem Using Single Step Algorithm. International Journal of Pure and Applied Mathematics, 86, 819-832. https://doi.org/10.12732/ijpam.v86i5.6
- 22. Nishad, A.K. and Singh, S.R. (2014) Linear Programming Problem with Intuitionistic Fuzzy Numbers. International Journal of Computer Applications, 106, 22-28.
- 23. Gani, A.N. and Abbas, S. (2014) A New Average Method for Solving Intuitionistic Fuzzy Transportation Problem. International Journal of Pune and Applied Mathematics, 93, 491-499. https://doi.org/10.12732/ijpam.v93i4.1
- 24. Angelov, P.P. (1997) Optimization in an Intuitinistic Fuzzy Environment. Fuzzy Sets and Systems, 86, 299-306. https://doi.org/10.1016/S0165-0114(96)00009-7
- 25. Hussain, R.J. and Kumar, P.S. (2012) Algorithmic Approach for Solving Intuitionistic Fuzzy Tansportation Problem. Applied Mathematical Sciences, 6, 3981-3989.
- 26. Hussain, R.J. and Kumar, P.S. (2012) The Transportation Problem in an Intuitionistic Fuzzy Environment. International Journal of Mathematics Research, 4, 411-420.
- 27. Hussain, R.J. and Kumar, P.S. (2013) An Optimal More-for-Less Solution of Mixed Constraints Intuitionistic Fuzzy Transportation Problems. International Journal of Contemporary Mathematical Sciences, 8, 565-576. https://doi.org/10.12988/ijcms.2013.13056
- 28. Ye, J. (2011) Expected Value Method for Intuitionistic Trapezoidal Fuzzy Multicriteria Decision-Making Problems. Expert Systems with Applications, 38, 11730-11734. https://doi.org/10.1016/j.eswa.2011.03.059
- 29. Wan, S. and Dong, J. (2014) A Possibility Degree Method for Interval-Valued Intuitionistic Fuzzy Multi-Attribute Group Decision Making. Journal of Computer and System Sciences, 80, 237-256. https://doi.org/10.1016/j.jcss.2013.07.007
- 30. Zimmermann, H.J. (1975) Description and Optimization of Fuzzy Systems. International Journal of General System, 2, 209-215. https://doi.org/10.1080/03081077508960870
- 31. Zimmermann, H.J. (1978) Fuzzy Programming and Linear Programming with Several Objective Functions. Fuzzy Sets and Systems, 1, 45-55. https://doi.org/10.1016/0165-0114(78)90031-3
- 32. Zimmermann, H.J. and Zysno, P. (1980) Latent Connectives in Human Decision Making. Fuzzy Sets and Systems, 4, 37-51. https://doi.org/10.1016/0165-0114(80)90062-7
- 33. Zimmermann, H.J. (1980) Testability and Meaning of Mathematical Models in Social Sciences. Mathematical Modelling, 1, 123-139. https://doi.org/10.1016/0270-0255(80)90012-3
- 34. Zimmermann, H.J. (1983) Fuzzy Mathematical Programming. Computers and Operations Research, 10, 291-298. https://doi.org/10.1016/0305-0548(83)90004-7
- 35. Thakre, P.A., Shelar, D.S. and Thakre, S.P. (2009) Solving Fuzzy Linear Programming Problem as Multi Objective Linear Programming Problem. Proceedings of the World Congress on Engineering, 2, 978-988.
- 36. Angelov, P.P. (1994) Approximate Reasoning Based Optimization. Yugoslav Journal of Operations Research, 4, 11-17.
- 37. Angelovs, P.P. (1995) Intuitionistic Fuzzy Optimization. Notes on Intuitionistic Fuzzy Sets, 1, 123-129.
- 38. Garg, H. (2018) A Linear Programming Method Based on an Improved Score Function for Interval-Valued Pythagorean Fuzzy Numbers and Its Application to Decision-Making. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 26, 67-80. https://doi.org/10.1142/S0218488518500046
- 39. Garg, H. (2018) Non-Linear Programming Method for Multi-Criteria Decision Making Problems under Interval Neutrosophic Set Environment. Applied Intelligence, 48, 2199-2213. https://doi.org/10.1007/s10489-017-1070-5






