Open Journal of Political Science
Vol.05 No.01(2015), Article ID:52975,13 pages
10.4236/ojps.2015.51003
A New Explanation of K. J. Arrow’s Impossibility Theorem: On Conditions of Social Welfare Functions
Zheng Yuan
Center for Chinese Public Administration Research, Sun Yat-sen University (CCPAR), Guangzhou, China
Email: Lpsyzh@mail.sysu.edu.cn
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 October 2014; revised 10 November 2014; accepted 6 December 2014
ABSTRACT
Social welfare function theory belongs to the cross disciplines of economics, sociology, management science and political science. The social welfare function conditions were first proposed by Kenneth Joseph Arrow, and served as the golden criteria in this field. For a long time, “the expressions of these conditions are not satisfactory”, as Arrow said himself, and he has continued to revise them. The author of this article has attempted to structure a mathematical expression that would meet Arrow’s conditions. We found that the conditions of “unrestricted domain” and “independent alternatives independence” could not always be expressed simultaneously. This led us to conduct further research on the relationships among Arrow’s conditions. We find that there are logical conflicts among some of these conditions, and we discuss these issues in this article.
Keywords:
Arrow’s Impossibility Theorem, Social Welfare Functions, Unrestricted Domain Condition, Independence of Irrelevant Alternatives

1. Introduction
Social welfare function is an important part of welfare economics or social choices; it concerns the objectives of social goals and the basic factors to be investigated in this filed. It is not a function in the general mathematical sense; rather it is a conceptual function or a collection of decision-making rules. In social choice theory, Arrow (1951) ’s impossibility theorem, or Arrow’s paradox, states that when voters have three or more distinct alternatives (options), no rank order voting system can convert the ranked preferences of individuals into a community- wide (complete and transitive) ranking under a pre-specified set of criteria. These pre-specified criteria are unrestricted domain, non-dictatorship, Pareto efficiency and independence of irrelevant alternatives. The above four criteria, or conditions, are merged by researchers from Arrow’s five original conditions. The specific form of social welfare function has no provision; this character can be both a weakness and an advantage. Note that social welfare function and social welfare are totally different concepts. The former deals with the choices of public policies, while the latter concerns the well-being of the society.
Arrow (1951) laid the foundation for the systematic study of the social welfare function, in which the key was to determine the criteria for such function. He found that the five basic conditions must be met for any reasonable social welfare function. On this basis, Arrow proposed his famous impossibility theorem that under these five conditions social welfare function did not exist. As it is commonly acknowledged that outside Arrow’s five conditions there is no reasonable social welfare function, the theorem of impossibility eliminated the existence of such function, which generated a profound impact on welfare economics. In the early 18th century, it was noted that collective decision-making could lead to conflicting results. Arrow solved this issue with a general conclusion and liberated many researchers from their unnecessary works in this filed. More importantly, Arrow’s impossibility theorem re-evoked numerous in-depth researches in welfare economics. For his outstanding contributions to the study of welfare economics, Arrow received the Nobel Prize in Economics in 1972.
Social welfare function refers to a collection of rules that turn every independent, dispersed voting of individual (political, economic or social) polymerization into corresponding social (public, collective) voting. Existing voting methods are unable to meet the basic rules of social welfare function for they all have some major drawbacks.
Arrow (1951)
proved the famous “impossibility theorem”: social welfare function that meets Arrow’s conditions, which are the only reasonable conditions for such function, does not exist. Based on critical personal cardinal utility, which is the basis of personal ordinal utility,
Arrow (1983: p.14)
gave the classical definition of social welfare function: “‘social welfare function’ will be meant a process or rule which, for each set of individual orderings
 for alternative social states (one ordering for each individual), states a corresponding social ordering of alternative social states, R”. Social welfare function based on personal utility, in mathematics called functional1, is not the common sense of function. The social welfare function can be expressed as
for alternative social states (one ordering for each individual), states a corresponding social ordering of alternative social states, R”. Social welfare function based on personal utility, in mathematics called functional1, is not the common sense of function. The social welfare function can be expressed as . Its input variables are the order relationships of individuals to different optional objects (or bills) and the output is the social sorting (social order relationship results when the polymerization occurs through the individual voting).
. Its input variables are the order relationships of individuals to different optional objects (or bills) and the output is the social sorting (social order relationship results when the polymerization occurs through the individual voting).
Which social welfare function is truly representative of the social (mass, the collective) choice? In other words, what is the standard criterion for social welfare function? K. J. Arrow’s conditions are the most authoritative such criteria. These conditions are not just pure abstract theory, but they are formulated based on voting (vote) practice analyses that take into account the basic, practical problems of a large number of voting. Arrow and many contemporary leading authors in this area developed these concepts.
There are enormous literatures on social welfare function. For example, Arrow (1951) , Mueller (1979; 2003) and Sen (1970) are the representative works. Arrow (1983) made further modifications to the five basic conditions.
Since the birth of the theorem of impossibility more than sixty years ago, Arrow and his followers had made “concrete” justifications for this theory and its opponents hadn’t been able to counter such justifications.
Here we try to give some counter examples for this theory and illustrate that this theory may not be true under certain conditions. In particular, we find that his condition 3 may be contradictory to the other conditions, and we propose a forum for discussion, which is the theme of this paper. As Arrow’s conditions on social welfare function are difficult to understand and numerous authors tried to explain his works, we will also spend two sections in explaining/discussing these conditions before giving our counter example.
The rest of this article is organized as below. In Section 2, we analyze Arrow’s five original conditions; in Section 3 we give particular discussion of the candidate independence condition; in Section 4 we give a counter example to the existence of the social welfare functions in Arrow’s Theorem of Impossibility; in Section 5 we propose an optional solution to this problem.
2. Analysis of K. J. Arrow’s Conditions
2.1. Introduction of K. J. Arrow’s Conditions
We first explain some commonly used notations/symbols in this filed. For candidates x and y, the notation xRiy Means that x is not worse than y in the opinion of individual i; xRy means that x is not worse than y in the opinions of the public; accordingly, xPiy and xPy mean that x is better than y in the opinion of individual i and in the opinions of the public respectively; xIiy and xIy mean that x and y have no difference in the opinion of individual i and in the opinions of the public. An environment S is the collection of all the alternative candidates, C(S) is the sub set of S:C(S) = {x in S:xRy for all y in S}. i.e., for any candidate in C(S), in the opinion of the public he/she is not worse than any other candidate in S. The notation A -> B means A implies B, and the notation A <-> B means A and B imply each other, i.e. A is the sufficient and necessary condition for B.
To better understand Arrow’s five conditions, we list the two expositions for each of these conditions, based on Arrow (1970; 1983) (see Table 1).
According to Arrow’s definition, social welfare function must simultaneously meet all the conditions set out in the above table.
Of Arrow’s five conditions, conditions 1 - 3 are relatively difficult to understand. Sen (2004) and other scholars have re-grouped and merged K. J. Arrow’s five conditions into four. Generally speaking, Arrow’s condition 3 is deeper than conditions 1 and 2.
Remark: the symbols R, P, I or R', P" and I" used in this article and their meanings are adopted from Arrow’s book “Social Choice: Personality and Multi-Criteria”, where R (or R') denotes the weaker order “no worse than”; P (or P') stands for the stronger order “better” than; and I (or I') stands for “no difference”.
2.2. K. J. Arrow’s Ideas for the Conditions of Social Welfare Function
In Arrow’s book “Social Choice: Personality and Multi-Criteria”, the five conditions for social welfare function are proposed to explain his idea. Below we discuss Arrow’s ideas on conditions 1 and 3.
Arrow’s idea on condition 1: for simplicity of exposition, it will be assumed that the society under study contains only two individuals and that the total number of conceivable alternatives is three. Since the results obtained are negative, the latter restriction is not real; if it turns out to be impossible to construct a social welfare function which will define a social ordering of three alternatives, then it will a fortiori be impossible to define one which will order more alternatives. The restriction to two individuals may be more serious; it is conceivable that there may be suitable social welfare functions which can be defined for three individuals but not for two. In fact, this is not so, and the results stated in this chapter hold for any number of individuals. However, the proof will be considerably simplified by considering only two ( Arrow, 1983: p. 14-15 ).
In order to deepen the reader’s understanding of condition 3, Arrow cites a classical example in the book “Social Choice: Personality and Multi-Criteria”: “suppose there are three voters and four candidates, x, y, z, and w. Let the weights for first, second, third, and fourth choices be 4, 3, 2 and 1, respectively. Suppose that individual 1and 2 rank the candidates in the order x, y, z, and w, while individual 3 ranks them in the order z, w, x and y. Under the given electoral system, x is chosen. Then, certainly, if y is deleted from the ranks of the candidates, the system applied to the remaining candidates should yield the same result, especially since in this case, y is deleted according to the tastes of every individual; but, if y is in fact deleted, the indicated electoral system would yield a tie between x and z” ( Arrow, 1983: p. 17 ).
Arrow specially highlighted: “alternatively stated, if we consider two sets of individual orderings such that, for each individual, his ordering of those particular alternatives under consideration is the same each time, then we require that the choice made by society be the same if individual values are given by the first set of orderings as if they are given by the second” ( Arrow, 1983: p. 16 ).
Arrow has been making modifications to condition 3 for quite some time.
Arrow (1983: p. 23-24) said: “interpretation of the impossibility theorem is given by examination of the meaning of conditions 1 - 5. In particular, it is required that the social ordering be formed individual orderings and that the social decision between two alternatives be independent of the desires of individuals involving any alternatives other than the given two (conditions 1 and 3)”. Arrow’s interpretation is the same as the understanding of condition 3 by Sen (1970) and Mueller (1979) .
In Arrow’s (1983) re-exposition of condition 3, the inexplicable C(S) and C'(S) are deleted (see chart 1), which reflects Arrow’s spirit of “I am never satisfied with the current exposition”, learning without stopping, and pursuit of truth and perfection.
Generally speaking, Arrow constantly absorbs others’ suggestions and makes refinements of these conditions. The exposition of Arrow’s condition 3 is more and more accurate and concise, but some of the expositions are too concise for the general reader to completely understand.
Table 1. Comparison of conditions for social welfare function.
2.3. Some Researchers’ Refinement of Arrow’s Conditions
Due to the difficulty in understanding Arrow’s conditions, many scholars made further refinements and modifications to these conditions. Among them, the works of Amartya Sen, William Vickrey and Dennis C. Mueller are representative. Below we discuss them.
Amartya Sen’s refinements
Sen (1970: p. 41-42) , in Sections 3.1 and 3.3 (p. 43-44), summarized Arrow’s five conditions into four:
Condition U (unrestricted domain conditions): The domain of rule f must include all logically possible combinations of individual sequences. The domain of the rule f must include all logically possible combinations of individual orderings ( Sen, 1970: p. 70 ).
Condition P (Pareto principle): For any pair, x, y in x, [∀ i: xPiy] → xPy.
Condition I (independence of irrelevant alternatives): Let R and R′ be the social binary relations determined by f corresponding respectively to two sets of individual preferences,
 and
and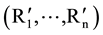 . If for all pairs of alternatives x, y in a subset S of X, xRiy ↔ xR'iy, for all i, then C(S, R) and C(S, R′) are the same.
. If for all pairs of alternatives x, y in a subset S of X, xRiy ↔ xR'iy, for all i, then C(S, R) and C(S, R′) are the same.
Condition D (non-dictatorship): there is no individual i such that for every element in the domain of rule f, x,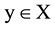 : xpi y → xPy.
: xpi y → xPy.
William Vickrey’s and Dennis C. Mueller’s refinements
Mueller (1979: p. 186) summarized Arrow’s five conditions by referencing the short and simple restatement of them from Vickrey (1960) :
1) Unanimity (The Pareto Postulate); 2) Non Dictatorship; 3) Transitivity; 4) Range (Unrestricted Domain); 5) Independence of Irrelevant Alternatives. The social choice between any two alternatives must depend on the orderings of individuals over only these two alternatives and not on their orderings over other alternatives.
Here, “domain” and “codomain” are characterizations of the same object from different points of view but their essential meanings remain the same. Domain is from the point of view of individual orderings while codomain is from the point of view of social welfare functional perspective. Mueller (1979: p. 186) suggested an additional explanation for codomain?“condition 4 perhaps requires an additional word of explanation. The notion of a universal alternative is not crucial here. What is implied by the Range Axiom is that the social choice process presumes that any ordering of the 3 alternatives X, Y and U is possible. The process is not established in such a way as to rule out possible orderings”.
Obviously, if limited codomain (or domain) deliberately intervenes in voting results, then it will not be possible to guarantee that all the alternative voting information (or the corresponding votes) will be treated equally, and as a consequence voting will not be fair and just.
Generally speaking, scholars have made new and relatively concise exposition of the original difficult conditions 1 and 2. While Arrow’s conditions 4 and 5 are easily understood, only condition 3 has remained unchanged, which is both a “gift” for newcomers and a last fortress for detailed explanation. Below we further explore Arrow’s condition 3.
3. Independent Candidate Independence Conditions (Arrow’s Condition 3)
“Of all the axioms, the independence of irrelevant alternatives has been the subject of the most discussion and criticism” Mueller (2003: p. 590) . The difficulty in understanding condition 3 (independence of irrelevant alternatives) has caused Arrow, Sen, and Mueller (2003: p. 590-596) to make special explanations of it. We discuss them below.
3.1. Arrow’s Further Explanation on Condition 3
For a better understanding of condition 3, Arrow (1983: p. 17) gave a classical example:
Suppose there are three voters and four candidates, x, y, z, and w. Let the weights for first, second, third, and fourth choices be 4, 3, 2 and 1, respectively. Suppose that individual 1 and 2 rank the candidates in the order x, y, z, and w, while individual 3 ranks them in the order z, w, x and y. Suppose that under the given electoral system, x is chosen. Then, certainly, if y is deleted from the ranks of the candidates, the system applied to the remaining candidates should yield the same result, especially since in this case, y is deleted according to the tastes of every individual; but, if y is indeed deleted, the indicated electoral system would yield a tie between x and z.
Arrow pointed out that: “y is after x in everyone’s ordering”, suggesting that he would strictly abide by the assumptions of condition 3 (for any individual i・・・) to analyze this example. According to Arrow’s note (p. 42 footnote), the above example and the suggestion from G. E. Forsythe (National Bureau of Standards) reinforced the importance of this example for the proof of independence of irrelevant candidates. This example was quoted verbatim in Mueller’s book Public Choice (1979, p. 197).
As for the results of social choice of “before” and “after” y is excluded, according to Arrow’s 1963 exposition and his 1983 re-exposition (see Collected Papers of Arrow (1983: p. 16) ): “then the social choice made from S is the same”, means that the orderings between all alternatives to S for “before” and “after” should be the same. Arrow (1983: p. 16) made an initial statement for condition 3: “alternatively stated, if we consider two sets of individual orderings such that, for each individual, his ordering of those particular alternatives under consideration is the same each time, then we require that the choice made by the society be the same if individual values are given by the first set of orderings as if they are given by the second”. He then gave another example ( Arrow, 1983: p. 16 ):
Suppose that an election is held with a certain number of candidates in the field, each individual filing his/her list of preferences, and one of the candidates dies. Surely, the social choice should be made by taking each of the individual’s preference lists, blotting out completely the dead candidate’s name, and considering only the orderings of the remaining names in going through the procedure of determining the winner. That is, the choice should be determined according to the preferences of all the individuals without the non-surviving candidate.
3.2. Amartya Sen’s Explanation of Condition 3
Sen (1970: p. 37) explained condition 3 (independence of irrelevant alternatives) in this way: “K. J. Arrow requires that social choice over a set of alternatives must depend on the orderings of the individuals only over those alternatives, and not on anything else, e.g., on rankings of ‘irrelevant’ alternatives that are not involved in this choice”.
Sen (1970: p. 37) first gave a popular explanation: “to give an analogy, in an election involving Mr. A and Mr. B, the choice should depend on the voters’ orderings of A vis-a-vis B, and not on how the voters rank Mr. A vis- a-vis Lincoln, or Lincoln vis-a-vis Lenin”.
Then Sen (1970: p. 910) gave another formal example: let us imagine that there are only three alternatives relevant for our consideration, x, y and z. Let individual 1 rank them in the order stated. Some experiment also reveals the following utility numbers for the three: 200, 110, and 100, respectively, but the numbers are unique up to a linear transformation. There is, thus, no natural correspondence between the utility numbers of the different individuals. A common convention is to attach the value 0 to the worst alternative, and the value 1 to the best. A linear transformation of the original set of numbers, therefore, yields 1 for x, 0.1 for y, and 0 for z. By a similar method of normalization let the utility numbers of two other individuals to be exactly the same, in particular, 1 for y, 0.6 for x, and 0 for z. If the community consists of these three candidates, then x wins over y, as the aggregate utility for x is 2.2, and that for y is 2.1. Next imagine that individuals 2 and 3 revise their opinion of z, an irrelevant alternative in the choice between x and y. They now regard z to be just as good as x. While everyone’s attitude to x and y has remained the same, nevertheless the utility numbers of x and y will change for persons 2 and 3. For them, x will now have value 0, while y will continue to get 1. Now y will win over x, as y having an aggregate utility of 2.1 as opposed to x’s 1. The social ordering between x and y is reversed by a change in the position of an irrelevant alternative, z.
For this,
Sen (1970: p. 89)
made an additional explanation: “any change in utility measures without a change of the individual orderings Ri’s must leave the social ordering R generated by any Social Decided Function (SDF) completely unchanged. This applies, naturally, also to such special cases of a CCR as a SWF and a SDF”. Now we are clear: for all i, as long as there is no change in individual ordering Ri (the corresponding ordering relationship “before” and “after” remain the same:
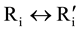 or
or
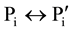 or
or ), any changes in utility measurement should not cause any change in the social ordering R.
), any changes in utility measurement should not cause any change in the social ordering R.
3.3. Dennis C. Mueller’s Explanation of Condition 3
Mueller (2003: p. 592) gave a detailed description of the motivation of Arrow’s condition 3: The preceding discussion indicates that an important objective of Arrow in imposing the independence of irrelevant alternatives axiom was to eliminate the possibility of individuals being made better off under a collective decision procedure if they did not state their true preference as inputs into the collective decision process. Vickrey (1960: p. 517- 519) speculated that immunity to strategic manipulation and satisfying the independence axiom were logically equivalent, and subsequently this insight was rigorously established by Gibbard (1973) and Satterthwaite (1975).
Mueller’s introduction to the motivation of Arrow’s condition 3 provides us an important tool for understanding the background and aim of Arrow’s condition 3, and for accurately mastering this condition and its extension.
“The strategy control” has two different forms: one is that Arrow guards against this situation: “everyone from any given environment S to make the choice should be not a matter of any candidates is in or not in S”. This form allows someone to choose a different voting control environment thereby allowing him/her to influence (or even change) the result of the social choice. We call his kind of situation “the strategy control.”
The second form is Dennis C. Muller’s expression: Some people give order relation of the “relevant” alternatives unchanged, but to different environment “Independent candidate” given different (preference) order relation?“strategic misstatement”.
Mueller (1979: p. 186) also gave a concise explanation of the initial motivation of Arrow’s condition 3: “the social choice between any two alternatives must depend on the orderings of individuals over only these two alternatives, and not their orderings over individual”. On this point, Mueller and Sen’s expositions are the same.
Mueller (1979: p. 197) observed: “one of K. J. Arrow’s objectives for invoking the axiom would seem to be to eliminate the permutation order such as program so that, ‘knowing the social choices made in pair-wise comparisons in turn determines the entire social ordering and therefore the social choice function C(S) for all possible environments’”. Mueller (2003: p. 590) refined this observation by stating: “here K. J. Arrow defends the axiom in terms of limiting attention to feasible alternatives only”.
“Strategic misstatement” in expression form is different from “the strategy control”, but they are essentially the same (see proof in appendix of this article). In this article we only analyze the form of “the strategy control”.
4. Contradiction between Arrow’s Condition 3 and Other Conditions
K. J. Arrow’s conditions are statements of rather esoteric mathematical logic and consequently any demonstration of a contradiction between Arrow’s conditions is very difficult. This study is an attempt to identify and describe a contradiction between Arrow’s conditions. Below is our analysis.
Assume that the candidate set for environment A is SA, candidate set for environmental B is SB.
4.1. The Original Intention of Arrow to Establishment Condition 3
4.1.1. A Hypothesis Provisions: SA = SB
For the necessary and sufficient condition of condition 3, logically it should be that the two optional object collections in different “environments” are equal, namely SA = SB, that is, in different environments the optional object sets should be the same. On the other hand, if there is an alternative Y1 of SB which is not in SA, let’s examine the necessary and sufficient condition in condition 3. Assume that individual k considers the ordering relationship between Y1 and Y2 in SB to be Y1RkY2. According to the necessary and sufficient condition, in environment A we still have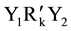 . But there is no Y1 in the set SA of alternatives in environment A, namely the relationship
. But there is no Y1 in the set SA of alternatives in environment A, namely the relationship
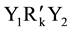 does not exist. To solve this contradiction, it seems that we should require SA = SB.
does not exist. To solve this contradiction, it seems that we should require SA = SB.
Next, we will illustrate, if we made the regulations SA = SB, then this will only be a seemingly reasonable voting rule, which does not accord with the practice of voting.
4.1.2. The Existence Value in Arrow’s Condition 3
As mentioned above, Arrow’s condition is based on voting practice. Arrow set up these conditions according to basic, practical problems found in large scale voting. It is not a pure theory or hypothetical research.
Assumption in the vote process makes a rational regulation: SA = SB. We will then face vote problems in practice: according to Dennis C. Mueller and other scholars’ explanations, further summary of condition 3 is as follows (see Sections 3.1 and 3.2). First, the original intention in establishing conditions 3 was to prevent voting control from becoming “strategic control”, thus the necessary condition of “strategic control” (or strategic misstatement) is SA ≠ SB. The concept of “strategy control” can be further divided into two situations: “strategy control” (to influence choice by manipulating the vote “environment”) and “strategic misstatement” (a behavior by the voter in order to obtain some optional object, or candidate deliberately does not express the real order relationship).
If at any time the “candidate sets” does not change, that is, SA = SB always holds, then there is no “strategy control” nor “strategy misstatement”.
But in practical voting we cannot assume that there is no “strategy control” nor “strategy misstatement” behavior.
Secondly, in voting practice often SB < SA or SB > SA. If we only vote in the common optional object set Sg, then it will cause some votes for the legitimate candidate to be rejected and, consequently “social welfare function” will be “illegal”.
The above analysis shows that if the rule SA = SB is imposed, then we will lose the existence value of Arrow’s condition 3.
4.1.3. Arrow’s Condition 3 Is Set Up for SA ≠ SB and for Preventing “Strategic Misstatement”
In the example given by Arrow (1983: p. 5) , under the given electoral system, x is chosen, then, certainly, if y is deleted from the ranks of the candidates, the system applied to the remaining candidates should yield the same result, especially since in this case, y is deleted according to the tastes of every individual; but, if y is in fact deleted, the indicated electoral system would yield a tie between, x and z.
Arrow’s concern is that if the situation were different from the above case then the election result would be “dependent on the obviously accidental circumstance of whether a candidate died before or after the date of polling” ( Arrow, 1983: p. 16 ). So Arrow (1983: p. 16) emphasized “the choice to be made among the set of surviving candidates should be independent of the preference of individuals for the non-surviving candidates”. In other words, the social choice made in the environments SA and SB = SA − 1 (SA − 1 means that one person is not in the candidate set SA) should be the same.
Dennis C. Mueller explained the purpose of Arrow’s condition 3: to avoid election manipulation people use “opportunity choice” to influence election results. The original intention of Arrow’s condition 3 is clear. Arrow’s condition 3 is a setting up for “candidate set” change in a different “environments” (SA ≠ SB) or preventing “strategic misstatement” (see Diagram 1).
4.1.4. On Background of Arrow’s Condition 3
Here, we are focused on the situation SA ≠ SB and will analyze the more common situations. We will assume that the voting organizers have the ability to predict the outcome in the original SA (Y1, Y2,・・・, Yi,・・・, YK), and that some candidates (the number is SK) will leave SA in another voting time (corresponding to the environment B).
In the above case, possibly N1 of the candidates will retire or pass away, N2 of them will relocate outside of the election district or withdraw from the company organization, etc, and N3 of them will leave for some other reasons. Let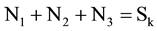 . Obviously, under these circumstances, the number of candidates in SA is greater than that of SB.
. Obviously, under these circumstances, the number of candidates in SA is greater than that of SB.
Or take the reverse of the above: for the alternative set SA in environment A, one can predict that at another election time (for environment B) there will be N4 new candidates (newly qualified candidates), N5 active members will relocate into this election district from other districts or company organization, etc. and N6 candidates will withdraw from election for some other reasons. Let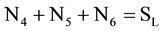 , then obviously the number of candidates in SB is greater than that of SA.
, then obviously the number of candidates in SB is greater than that of SA.
Thus, from environment A to environment B, the set of candidates SA becomes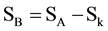 ; or from environment B to environment A, the set of candidates SB becomes
; or from environment B to environment A, the set of candidates SB becomes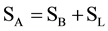 .
.
In these cases, the voting controller can control the voting to some extent in the seemingly strict voting method. This is what Arrow worried about. Condition 3 allows SA ≠ SB to prevent the voting controller to affect election results “legally”, by using “opportunity choice” (voting arranged in different environments for some purpose).
Here we generalize Arrow’s classical example (see Section 3.2). We need the following hypothesis
P: for a vote on activities, possible candidate set in environment A is SA (Y1, Y2,・・・, Yi・・・ Yk), and possible candidate set in environment B becomes SB (Y1, Y2,・・・, Yi, Yr,・・・, Ys) for several reasons. Obviously, the candidate sets of environment A and that for environment B are different.
It is also possible to have a number of different environment conditions (N) (see Table 2). But, in theory, we only need to analyze two different environments, as we will do latter.
In case SA ≠ SB, the controllers may control voting to some degree (according to a particular purpose by choosing different voting environments) and they are seemingly legal, this is one of K. J. Arrow’s worries for the case of SA ≠ SB. So K. J. Arrow imposed his condition 3, in order to prevent the vote manipulation using the way of “strategy control” to “legally” influence the voting results.
Diagram 1.The relationship between Arrow’s condition 3 and candidate sets in different environments.
Table 2. (In hypothesis P) Candidate set changes in different environments (for two different “environment” situations).
4.1.5. Review of Elements of Arrow’s Condition 3
In order to make the subsequent analysis somewhat easier, below we give a brief review of Arrow’s condition 3.
1) The environment of voting is a function related to voting background (how, where, etc.);
2) The candidate set refers to a vote on the problem of the “all the candidate” or “every possible solutions summary” in different conditions; the candidate sets may not be all the same;
3) Necessary and sufficient condition: for all people voting in different environments (say A and B), the order relationship should remain unchanged, namely the sufficient and necessary conditions should be met: xRiy ↔ xR'iy (Ri represent the order relation in environment A, of arbitrary two optional object, x, y; R'i represent the order relation in the environment B be given to the same two candidates x, y). Because SA ≠ SB, so the subscript i value ranges of both ends (in the necessary and sufficient condition) are not completely the same. Essentially, the necessary and sufficient condition can only constrain the public optional object set Sg which belongs to a different environment optional object set from SA and SB. This is the key, and helps to explain expression’s (I) and (II) of Section 4.2.2;
4) Social Order: it deals with the voting results of all voters for each candidate;
5) Arrow’s condition 3 requires that in different environments (with A and B, say) of voting, if the necessary and sufficient conditions are satisfied, then all optional objects have the same social order. In other words, for all optional objects of SA and SB, the social order in the two situations (environments) must be the same. Let SN be the “not optional object” set, it’s not an empty set, and Sg the “the optional object” set. Let SM = Sg + SN, which aligns with Arrow’s condition 3 regulation. When Sg meets the sufficient and necessary conditions, no matter what sequence relationship between the optional objects in SN and those in SM, social choice results are not affected by the optional object order relation and are not subject to any influence from changes. This reflects the social choice results for independence for the “independent candidate”. As stated in Sen (1970) ’s explanation: “to give an analogy, in an election involving for Mr. A and Mr. B, the choice should depend on the voters’ orderings of A vis-a-vis B, and not on how the voters rank Mr. A vis-a-vis Lincoln, or Lincoln vis-a-vis Lenin”.
4.2. Rule Conflicts for Condition 3
We continue to look at condition 3 and we find it has some rule conflicts: to eliminate “strategy control”. Arrow’s condition 3 reminds us to consider social election in different environments, in which: SA ≠ SB. Condition 3 requires that under the situation SA ≠ SB (sets of alternatives are SA and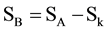
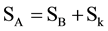
4.2.1. Qualitative Analysis for Conflict of Arrow’s Condition 3 with Unrestricted Domain Condition
“Unrestricted domain” conditions stipulates that a social choice process should accept all the information of voters on every voting. It is said that for alternatives Y1, Y2, we should make full use of all information of all voters voting on options Y1, Y2, and that of Y1, Y2 each compared with all the other alternatives Yj, Yi,・・・ Don’t allow, abandon or limit parts of voting information (see the following playback window).
Now we investigate the conflict in Arrow’s condition 3 with the unrestricted domain condition.
“Irrelevant alternatives” Yi+1・・・ YK appear only in one environment (such as A) and not in another (such as B). The order relations of “irrelevant alternatives” Yi+1・・・ YK can drift outside of the sufficient and necessary conditions of condition 3, that is to say, the order relations of Yi+1・・・ YK within each other, that between the set Yi+1・・・ YK and the set Y1, Y2,・・・, Yi, and that of Y1, Y2,・・・, Yi within each other can be any given ones, according to the requirements of Arrow’s conditions 3, as long as they appear in different environments. When the order relation between “relevant optional objects” remains unchanged, then the Social order relation of “relevant optional objects” in the different environments should be the same.
For our analysis, unless a special section mapping function is specified, the common alternatives are set strictly on the function value SG. And for setting variables other than in set SG(Yr,・・・, Ys), the function value is fixed. From the point of pure mathematics, such a function exists. But from the public choice’s “social welfare function” perspective, it is directly set and the social choice result has nothing to do with the order relation of variables (Yr,・・・, Ys)! Such “social welfare function” essentially repels the order relation information of variables (Yr,・・・, Ys), so this obviously conflicts with “unrestricted domain” condition. In addition, the same social welfare function is used for candidates in and outside the set SG while taking different “recount rules” respectively, clearly this violates the basic principles of collective (public) voting.
4.2.2. Conflict of Condition 3 with Unrestricted Domain Condition (Quantitative Analysis)
The definition of the “Independence of irrelevant alternatives” (K. J. Arrow’s condition 3) made from Amartya Sen is more specific: “if for all pairs of alternatives x, y in a subset S of X, xRiy ↔ xRʹiy, for all i, then C(S, R) and C(S, R′) are the same” (see Section 2.3). Arrow’s condition 3 requires that: voting in different environments, the social choices C(S, R) and C(S, Rʹ) made on “relevant alternatives” set Sg should be the same.
Then we observe voting from the social process point of view (voting technology link), and focus on the three concepts involved in Arrow’s condition 3 which are closely linked together: 1) “irrelevant candidate independence conditions”; 2) “unrestricted domain conditions (domain justice)”; 3) Arrow’s expression of the result of “irrelevant candidate independence conditions”: “then the social choice made from S is the same whether the individual orderings are R1, R2 or R1, R2” (see Table 1: condition of the expression of 3).
We express Arrow’s explanation of his classical example of (see this article page 5) “irrelevant candidate independence conditions” using mathematical language as follows:
According to Arrow’s classical example, the voting function (Social welfare function, or functional) in environment A is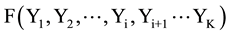
Later on in environment B, some candidate(s) passed away, they (denoted by Yi+1 ・・・YK) will be excluded from the set of alternatives. Then the voting function (Social welfare function, or functional) in environment B can be written as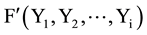
We input the order relationship between candidates into the voting function F and F' and then output the results of the voting (social order). Arrow’s condition 3 requires that when the sufficient and necessary condition xRiy ↔ xR'iy is met, then the following identity is established according to Arrow’s requirements: voting results in environments A and B are always the same: “then the social choice made from S is the same”. According to the definition of social welfare function (or functional3), we get the following equation:
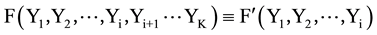
In expression (1), F is the voting result (ordering relation set) about the alternatives of all the voters in environment A, while F' is the voting result (ordering relation set) of the alternatives in environment B. The right side of expression (1) only contains variables Y1, Y2,・・・, Yi, so actually expression (1) is an eternal equation of the social order on the “relevant” candidate set Sg (where the candidates are Y1, Y2,・・・, Yi).
As mentioned in Section 4.1.5: the candidates Yi+1・・・ YK are outside the “relevant candidate” set Sg, they are free variables, and do not suffer from the constraint of the sufficient and necessary conditions of Arrow’s condition 3, every voter could arbitrarily give the ordering relationships about Yi+1・・・ YK with each other, and Yi+1・・・ YK with Y1, Y2, …, Yi.
Let Y be the order relationships among Y1, Y2,・・・, Yi; while X is the order relationship between every pair within the set Yi+1・・・ YK and between the sets Yi+1・・・ YK and Y1, Y2,・・・, Yi.
Then (1) is simplified as (2):
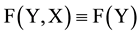
From the social (collective) voting perspective, at both sides of Equation (1) (or expression (2)), F and F' follow the same rule; Analysis of the expression (1) (or expression (2)) based on mathematical principles reveals that F and F' are the same function.
The condition of independence of irrelevant candidates requires that expression (1) (or (2)) be an eternal equation. In expression (2), X has no definition.
But, Arrow’s conditions for expressions (1) and (2) meet the “unrestricted domain” condition, too. To see this, for expression (1) (or (2)) to be an eternal equation, we have to apply a special limit to the order relationship of optional object Yi+1・・・ YK between each other and the order relationship between the sets Yi+1・・・ YK and Y1, Y2,・・・, Yi. For example, let the values of the functions of (1) (or (2)) have nothing to do with the order relationship of Yi+1・・・ YK or with each other and those with Yi+1・・・ YK or with each other; or allow expression (1) (or (2)) to only adopt the ordering information of relevant candidates set SG(Y1,Y2,・・・, Yi), and reject the ordering information of the relationship of irrelevant candidates which is outside of SG. Then we have the following results:
First, expression (1) (or (2)) shows that the ordering relationships among the “irrelevant candidates” Yi+1・・・ YK which is outside of the relevant set SG, and the ordering relationships among Yi+1・・・ YK with other candidates are all ineffective?now we restrict the ordering relationships of some candidates, thus the results conflicts with the condition of unrestricted domain.
Secondly, we may assume that the order relationship of “irrelevant alternatives” Yi+1・・・ YK between each other and the order relationship of Yi+1・・・ YK with Y1, Y2,・・・, Yi, as well as between each other are all effective. But this order relationship is not bound by the sufficient and necessary condition of condition 3. In different envi- ronments, they can, within order relationships R, P, and I, form any different combinations, because the order relationships are effective. The order relation for voting results (social order) must produce substantial effects. Thus, the social choice F'(Y1, Y2,・・・, Yi) in environment B (which includes candidates Y1, Y2,・・・, Yi) must not be equal to the social choice F(Y1, Y2,・・・, Yi,・・・ YK) in environment A (includes candidates Y1, Y2,・・・, Yi, Yi+1,・・・ YK), and consequently F'(Y1, Y2,・・・, Yi) ≠ F(Y1, Y2,・・・, Yi,・・・ YK).
And Arrow’s condition 3 still requires that even in different environments the social order must remain the same. This is clearly a paradox.
“The strategy control” and “strategic misstatement” are seemingly different, but they are essentially the same (see Appendix).
5. The Proposed Optional Solutions
According to the above analysis, there is contradiction in Arrow’s condition 3, but the essence of the meaning of this condition is difficult to understand. According to the essential requirement 3 (with Dennis C. Mueller’s explanation for example) of Arrow’s conditions, we can design some easier-to-understand informal (rather than formal) conditions to meets Arrow’s conditions (including 3 conditions) of social welfare function. These informal conditions agree with those of Arrow’s in nature.
5.1. Alternative Object Collection “Maximize” (to Prevent the “Strategy of Manipulation”)
For every important (significant) collective vote activities, through demonstration, institutionally constructed to determine the activity of a vote within the time span for possible “maximize” alternative set of objects in different “voting environment”, alternative sets of objects are the same (unchanged), so Arrow’s classical example of “strategy of manipulation” will not happen (if within this time span, there is “nothing to do” alternative object “died”, then at least for the alternative object organizers, this is “irrelevant” to those “relevant” alternative object result of the vote, i.e., the vote of people is dependent on all voting), we will request the “death” of the candidate objects be included in the original collection of objects (to vote for different “alternative unrelated object” is not the same) and to maximize the voter groups information with “hidden” death of the candidate object; On the other hand, we inform all voters to vote in accordance with their own original ideas, so there is no “strategic misrepresentation”.
For the voters, as they do not know what specific social welfare function will be used, they do not know if they should increase or decrease the “irrelevant alternative object” on voting (election), therefore, manipulation will have no effect
If we still suspect that voters might do “strategic misrepresentation” in the voting process, then we vote in accordance with the following program design process.
5.2. Set up a “Social Welfare (Quasi-) Library” Program (to Prevent the “Strategic Misrepresentation”)
In theory, prevent the “strategic misrepresentation” is the most difficult task, because it is entirely a psychological behavior to voters. We have psychological and behavioral control in the voting system, which will prevent “strategy misrepresentation” to happen. Clearly, the ordinary institutional constraints will fail!
Social Welfare (quasi-) function: that does not satisfy Arrow’s condition in the form of the three requirements, but meet Arrow’s other conditions (in the form of other requirements) of the welfare function. In this article we call such function social welfare benefits (quasi-) function.
5.2.1. The Basic Idea of Social Welfare (Quasi-) Library
In public examination, if there is only one set of questions, some candidates may “guess” the answers in advance; if there are many sets of questions consisting of a test database, the test organizers randomly selected a set of questions, then the “guess” behavior is basically useless. Following this line of thought, we construct a number of social welfare benefits (quasi-) function consisting of (quasi-) library. The inspiration is that: for an intended “strategic misrepresentation” in the vote, if there are multiple social welfare (quasi-) function options, let the actual social welfare (quasi-) function be kept strictly confidential until all the voters finished their vote. In this way, the effect of “strategic misrepresentation” can be reduced to the minimal level.
5.2.2. “Constitutional” Principle of Social Voting
The pioneers Buchanan & Tullock (1965: p. 56-58) in their long-term studies of social welfare real-valued function and tireless efforts to promote social selection process “unanimous consent” proposed some guidelines: “choose their own decision rule in a group selection・・・, one way to avoid the methodology seems hopeless predicament, is to introduce some sort of unanimity or completely consensual constitutional rules on the ultimate level of decision-making.”
“Constitutional” principle of social voting (see the related discussions of Buchanan): refers to the highest standards of social voting. From the social vote “constitutional” principle point of view, Kenneth J. Arrow’s conditions of “agreed postulate, non-authoritarian postulate, transitive postulate, range (unrestricted area) axiom is the basic principle of social selection process apparently” are “constitutional” principle of social voting.
In addition, assume that all of Arrow’s conditions of the social welfare function (so it must be non-unique) are met, we will then face the following basic questions:
Arrow’s social welfare function has a number of conditions, while voting for the same sequence of individual variables (sequence), different social welfare function will give different results of the same social order. So, in a voting process, which social welfare function is the only fair and just to use? Obviously, an organizer’s subjective choice of social welfare function will be unable to avoid the suspicion of “strategic manipulation”.
It seems from the point of fair and just principles of practice that, for any community (collective) vote, the social welfare function should be randomly selected from a collection of social welfare functions.
Therefore, the “constitutional” principle of social voting should include voting methods (social welfare function) of the random principle.
5.3. Preventing the “Strategic Misrepresentation”
“Strategic misrepresentation” often “misrepresented” the voter who knows in advance the specific form of the social welfare function, then “exercise” in advance to determine what “strategic misrepresentation” to get the desired effect.
If the specific social welfare (quasi-) function is not announced before the vote, then the “strategic misrepresentation” should not happen. A mechanisms should be set up under community supervision by a public authority to randomly select a social welfare (quasi-) function from the “social welfare (quasi-) function library”, and each individual votes with the selected social welfare (quasi-) function to obtain a social voting results. This can minimize the “strategic misrepresentation” (while preventing the “strategy of manipulation”), or with (using probability and statistics, hypothesis testing and other auxiliary method) “strategic misrepresentation” controlled within acceptable level.
6. Epilogue
As Roger d. Congleton, the successor of James M. Buchanan, mentioned ( Congleton, 2002 ): “like other science, there are many open questions in the field of public choice, like floating-debris in ‘swamp’. Their current foundation is somewhat sufficient; however, when making further exploration, we can find that the publicly known research and its foundation are not so sufficient”. That is to say that some of the theories in social choice are still immature. The original works of Duncan Black, James Mcgill Buchanan, Kenneth J. Arrow, G. Tullock, Mancur Olson, Amartya K. Sen, Dennis C. Mueller, etc. created great beginning in the theory of social choice, such theory looks like finished construction of a large estate project, but there are still lots of works need to be done for its perfection: regional planning and commerce, educational facilities, residential property management, building area road beautification, building internal decoration, water, electricity, gas facilities installation・・・ etc.
Arrow’s condition is the basic tool for the judgment of social welfare function. Understanding and analysis of these conditions will enable us to have clear concept in this filed. Analysis and exploration of the underlying sub conditions and is a way to better the development of this judgment tool. For it to be more conveniently applied, this has obvious important theoretic and practical values. We hope that this article can raise the attentions of more scholars to join the explanation of Arrow’s conditions, and to show their better and accurate understandings of these conditions.
7. Final Conclusion
It is not that there is no social welfare function which does not satisfy Arrow’s conditions, rather that there are contradictions and conflicts in Arrow’s conditions (“unrestricted domain condition”, “independence of irrelevant alternatives condition” and “Pareto condition”)! Thus, we should re-check, discuss and revise Arrow’s conditions!
Funding
This article is supported by the National Social Science Fund, P. R. China. Grant No. 06BZZ027.
The results won the Sun Yat-sen University third phase funding of the “985 project” (the study of contemporary Chinese government and political significant transformation project).
This research was funded by the prestigious funding project “Theoretical Research in Guangdong” (Approval number: 1306).
References
- Arrow , K. J. (1951). Social Choice and Individual Values. New Heaven, CT: Cowles Foundation, Yale University.
- Arrow, K. J. (1970). Social Choice and Individual Values (2nd ed.). New Heaven, CT: Cowles Foundation, Yale University.
- Arrow, K. J. (1983). Social Choice and Justice. Cambridge, Massachusetts: The Belknap Press of Harvard University Press.
- Buchanan J. M., & Tullock, G. (1965) The Calculus of Consent: Logical Foundations of Constitutional Democracy. Ann Arbor, MI: University of Michigan Press.
- Congleton, R. (2002). The Future of Public Choice. The Sixth International Conference in Public Choice, Japan, 21 July 2002.
- Mueller, D. C. (1979) Public Choice. London: Cambridge University Press.
- Mueller , D. C. (2003) Public Choice (3th ed.). London: Cambridge University Press.
- Sen, A. K. (1970) Collective Choice and Social Welfare. Cambridge, Massachusetts: Belknap Press of Harvard University Press.
- Vickrey, W. (1960). Utility, Strategy, and Social Decision Rules. The Quarterly Journal of Economics, 74, 507-535. http://dx.doi.org/10.2307/1884349
Appendix
1) “Strategic mistake expression” concept
We can use mathematical language to turn “strategic mistake expression” into a general statement: suppose that Sg is a “related” candidate set while
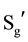

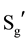

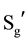
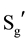
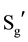
2) Analysis to “strategic mistake expression” facing contradiction
We assume that:
a) In environments A and B, all the voting order relationships among the optional objects Y1, Y2,・・・, Yi are the same (the provisions of the necessary and sufficient conditions). We use C1 to denote this condition; In environment A, the order relationships among Yi+1・・・ YK and that between the sets Yi+1・・・ YK and Y1, Y2,・・・, Yi, are fixed. We use C2 to denote this condition;
b) In the environment B, part of the voters are endowed by Yi+1・・・ YK about their mutual order relationships among each other and that between the sets Yi+1・・・ YK and Y1, Y2,・・・, Yi, “painstakingly against their wills,” which is the “strategic misstatement”.
Given the above our analysis is as follows:
K. J. Arrow’s condition 3 requires that no matter what “strategic misstatement”, the mutual order relationships among Yi+1・・・ YK and between the sets Yi+1・・・ YK and Y1, Y2,・・・, Yi should keep unchanged, and so the following equation must be true:
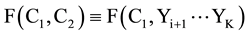
The left hand side of (3) represents social voting results of relevant optional objects Y1, Y2,・・・, Yi. in the environment A. The right hand side of (3) represents social voting results of the optional objects Y1, Y2,・・・, Yi, Yi+1・・・ YK. in environmental B.
Therefore, in essence, “the strategy control” and “strategic misstatement” will face the same contradiction (see Section 4.2.2 (Quantitative analysis)).
NOTES
1Functional domain is a set of functions, and range is the set of real numbers or a subset of the set of real numbers, which is from function space to number field mapping.
2In our repeated attempts to construct social welfare functions satisfying K. J. Arrow’s conditions, whenever coming to the intersection of the unrestricted domain condition and the independence of irrelevant alternatives condition when the sets of alternatives in the two “environments” are not all the same, we found that the two conditions cannot be satisfied simultaneously. This motivated us to explore the relationships among K. J. Arrow’s conditions.
3Functional domain for a set of functions (such as order relation set), and the range is the set of real Numbers or a subset of the set of real Numbers, the promotion, that is to say, is from function space to number field mapping.






