Open Journal of Soil Science
Vol. 3 No. 5 (2013) , Article ID: 36406 , 7 pages DOI:10.4236/ojss.2013.35026
Geostatistical Analysis of Soil Nutrients Based on GIS and Geostatistics in the Typical Plain and Hilly-Ground Area of Zhongxiang, Hubei Province
![]()
1State Key Laboratory of Coal Resources and Safe Mining, China University of Mining & Technology, Beijing, China; 2College of Geoscience and Surveying Engineering, China University of Mining & Technology, Beijing, China; 3College of Resources and Environment, Huazhong Agricultural University, Wuhan, China.
Email: 773858721@qq.com
Copyright © 2013 Yangbo Xu et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 24th, 2012; revised January 24th, 2013; accepted February 4th, 2013
Keywords: Zhongxiang; Soil Nutrients; Geostatistical Analysis; Geostatistics; GIS; GS+; SPSS
ABSTRACT
Techniques of geostatistics are used to perform traditional statistical analysis and spatial structural analysis with ArcGIS, geostatistical software GS+ and statistical software SPSS in order to obtain the knowledge of characteristics of distribution and spatial variability of soil nutrients in different parts of Zhongxiang, Hubei Province. Some skewed values appeared during the analyses. To decrease the influence of those skewed values, domain processing and Box-Cox transformation were used. The results indicated spatial variability of Total N, Avail. P, rapidly-available potassium (R-Avail. K) and effective zinc (Effect. Zn) was strong, that of organic carbon (Org. C), effective molybdenum (Effect. Mo) and effective copper (Effect. Cu) was medium while that of others was weak. Fitted model of Total N, R-Avail. K and Effect. Mo was spherical model, that of Org. C and Effect. Zn was exponential model, while fitted model of Avail. P and Effect. Cu was Gaussian model. Ratio of variability caused by random factors to overall variability was large. What’s more, the ranges of spatial autocorrelation of soil nutrients had much difference. The smallest value was 3600 m in Effect. Zn while the largest was 77970 m in Org. C. Other characteristics were also included. The study is helpful to soil sampling design, to make people realize the influence of Han River to spatial variability of soil nutrients in this area, and to spatial interpolation and mapping.
1. Introduction
As one of the basic conditions for crops to grow, soil has been changing under the combined influence of different factors (X.W. Zhou, et al. [1]).The condition of soil nutrients is relevant with the speed of crop growth, state of development, yields and arrangement of crops, proper application of fertilizers and anthropic factor etc. Due to the combined effect of these factors, soil nutrients, nutrients content and patterns of distribution differentiate in different areas.
A lot of scholars have made studies about relevant problems. For example, Y. L. Wang et al. [2] analyze soil nutrient content and the state of applied fertilizers in the northern plain of Henan province, which provides theoretical basis for the proper utilization of soil resources, scientific manuring for agricultural production and promoting combined revenues of agricultural production.
Some scholars, such as T. L. Mu and Q. J. Wang [3], have discussed erosion mechanism of soil nutrients using the technology of artificial rainfall simulation and positioning observation. Some like J. P. Liu et al. [4] elaborate the problems of blind fertilization and maximum utilization of agricultural resources using geostatistical functions of GIS when studying spatial variability characteristics of soil nutrients in the core demonstration plot of precision agriculture in Jilin province. Some [5-9] have described characteristics of spatial variation of soil nutrients in the specific areas. Others [10,11] have studied the utilization of geostatistics in Soil Science. In fact, actual requirements, local terrains and climate et al. should be considered in the course of study.
Taking Zhongxiang where hundreds of soil sampling points are set as the research object, this article analyzes the content, characteristics of distribution and patterns of spatial variability etc. of some soil nutrients in this area. Then it penetrates into studying the characteristics of spatial variability in Zhongxiang as a whole or part and meanwhile discussing the influence of Han River to the distribution of spatial variability of different nutrients horizontally. Besides, it can also provide decision support [12] and some guidance for proper fertilization based on the actual content of soil nutrients and the demand for them.
2. The General Situation of Study Area
Zhongxiang, whose longitude is between E112˚07' and E113˚00' and latitude is between N30˚42' and N31˚36', lies in the northern part of Jingzhou and the middle of Han River. It belongs to central Hubei downland and its shape looks like a peach. From the general trend, terrain of northeast is higher than that of southwest. Zhongxiang is divided into two parts by Han River both sides of which are broad alluvial plains. From near to far successively are downland, upland and mountainous area. The overall area of the city, where plain lake area, downland, upland and mountainous area occupy 28.655%, 37.16%, 13.76% and 20.43% relatively is 4417.8 square kilometers. The terrain map of Zhongxiang is as Figure 1.
Locating in the mid-latitude area, Zhongxiang belongs to north subtropical monsoon climate area. The highest air temperature is in July and its average temperature in years is nearly 27.9˚C; while the lowest temperature is in January with average lowest temperature 3˚C. And average temperature in years is nearly 15.9˚C. Annual average precipitation is nearly 952.6 mm. Month that has rainfall in the most is July, and its monthly average pre-
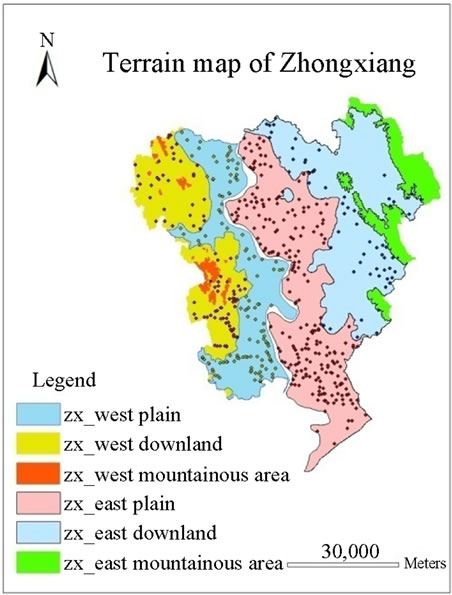
Figure 1. Terrain map of Zhongxiang.
cipitation is 164.2 mm. However, December is month raining the least with monthly average rainfall being 21.6 mm.
3. Experimental Methods
3.1. Data Acquisition
The two parts, west Zhongxiang and east/Zhongxiang, divided by Han River in Zhongxiang are again divided into plain and downland respectively. And there are 208 points in the west Zhongxiang, of which 120 points are in the plain and 88 points in the downland, and 290 points in the east Zhongxiang, of which 230 points are in the plain and 60 points in the downland. The distribution diagram of soil sample points is as Figure 2, and the amount of soil sample points of every area in Zhongxiang is as Table 1.
Primarily it is necessary to collect soil samples of the 498 points and information including position of sampling points, landforms, parent material of soil, climate, soil thickness and fertilization condition etc. in Zhongxiang, meanwhile position the sampling points using positioning function of GPS and undertake field investigation. Then analyze the collected soil samples, measure the content of different soil nutrients and analyze their physical and chemical characteristics. Finally analyze the data to obtain the characteristics of distribution and spatial variability of soil nutrients in Zhongxiang.
3.2. The Process of Data Processing
Firstly collect information from soil samples of Zhong-
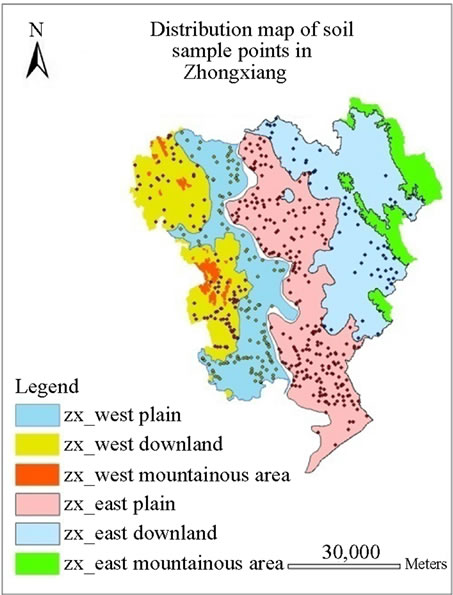
Figure 2. Distribution map of soil sample points in Zhongxiang
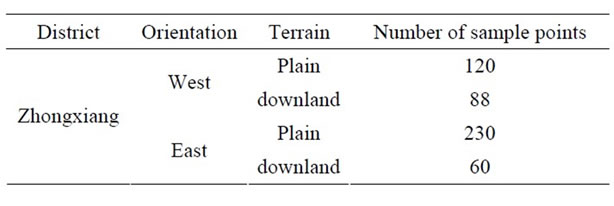
Table 1. Number of soil sample points in the every area of Zhongxiang.
xiang and input them into the computer. Then carry on traditional statistical analysis to see whether they fit normal distribution or not. If they do, then carry on spatial structural analysis. Otherwise use domain processing and Box-Cox transformation to process the original data and then test the normality of transformed data. The process is as Figure 3.
3.3. Data Treatment Using Computer Software
Original data are analyzed using different computer software. Figures 1 and 2 are produced in the ArcMap of ArcGIS (version 9.2). Traditional statistical analysis is performed using GS+ (version 7.0) and SPSS (version 19), while the spatial structural analysis is carried out only using GS+ (version 7.0). In traditional analysis, most values, except the value of k-s test which is produced by SPSS, are produced with GS+.
3.4. Data Transformation
As some raw data of soil nutrients in Zhongxiang is skewed, it’s necessary to perform data transformation to achieve a good analysis result. Therefore different forms of transformations like logarithmic transformation, domain processing, Box-Cox transformation and the combination of every two of them are tried. At last, it seems that it is effective to use domain processing firstly and then to use Box-Cox transformation. Though most nutrients does not pass normality test yet after these transformations, it does decrease the value of coefficient of variation, skewness and kurtosis of these nutrients to some degree.
4. Results and Analyses
4.1. Traditional Statistical Analysis
Use soil nutrient data of sampling points in Zhongxiang to acquire information of the state of soil nutrients content in the area, see Table 2.
In Table 2, it is obvious that medium value and average value of Org. C, Total N, Avail. P, Effect. Mo, Effect. Zn, Effect. Cu and W.S.S. B are similar, while that of R-Avail. K etc. have much difference. The reason why the phenomenon happens is that the nutrient content of R-Avail. K etc. is influenced by unusual values. Coefficient of variation represents the discrete degree of random variables. In general, it’s weak variation when C.V. < = 0.1, medium variation when 0.1 < C.V. < 1, strong variation when C.V. > 1. Among these elements coefficient of variation of Total N whose value is 29.72% is smallest; that of Avail. P is biggest, reaching 99.99%, and it has strong spatial variability.
As for the range of soil nutrients, content range of the same element changes much, such as R-Avail. K whose maximum is 67.2 times larger than minimum; and range of variation of different nutrients content is large. For example, range of variation of R-Avail. K is 1778.4 times larger than that of total N.
Skewness is presentation of degree of asymmetry of probability density distribution curve. It’s positively skewed when Sk > 0, and smaller data concentrate; it’s symmetrical when Sk = 0; it’s negatively skewed when Sk < 0, and bigger data are more concentrated. According to Table 2, the 8 elements is all positively skewed, that’s, smaller data concentrate.
Kurtosis shows characteristics of peak value corresponding to the average value in probability density distribution curve. The peak value of probability density distribution curve is bigger than that of normal distribution when KU > 0, equal to that of normal distribution when KU = 0, smaller than it when KU < 0.
In terms of k-s test, it is normal distribution when the k-s value is bigger than 0.05. However, all the original nutrient data do not fit normal distribution. That may have something to do with Han River which separates Zhongxiang into two parts. Through domain processing and Box-Cox transformation, only Effect. Zn corresponds to normal distribution, see Table 3.
The effect of these transformations is not as good asexpected. Nevertheless they have decreased the values of C.V. of almost all the nutrients discussed in this article. Therefore as a contrast, all the data is processed through domain processing and Box-Cox transformation successively to prepare for the analysis subsequently.
4.2. Spatial Structural Analysis
Due to abnormality of most element data which are through domain processing and Box-Cox transformation, all the data are firstly processed through the same course as a contrast, and then are conducted spatial structural analysis. The results of the analysis are like Table 4.
The table shows that spherical model is the best fitted model, occupying 37.5%; then it’ s Gaussian model and exponential model, both accounting for 25%; Finally it’s linear model, taking up 12.5%. Nugget reflects degree of random variability. Sill represents the overall spatial variability degree, including random variability and structural variability. Ratio of nugget to sill (C0/(C +
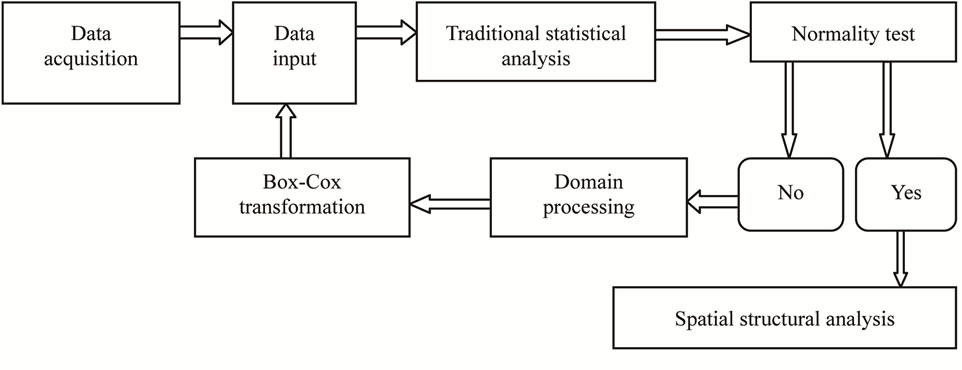
Figure 3. Data flow chart.
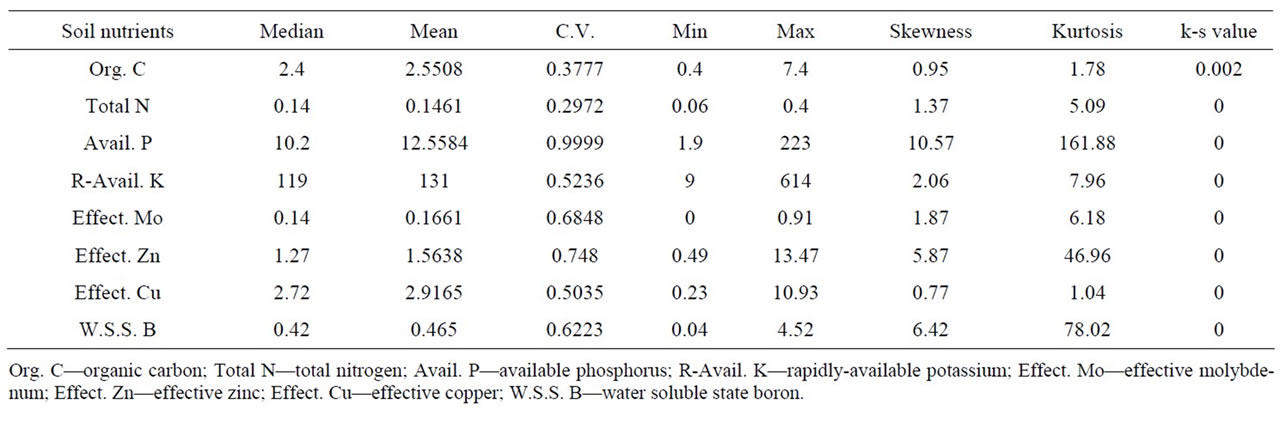
Table 2. Results of soil nutrients for typical analysis and k-s test (n = 498; units of median, mean, min and max in mg/kg).
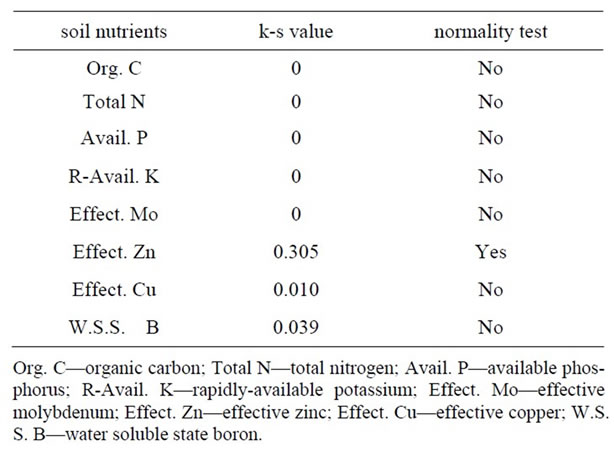
Table 3. k-s test of transformed data.
C0), mirrors the ratio of random variability to overall spatial variability. variable has strong spatial autocorrelation when C0/(C + C0) <25%, that’s, random factors occupy the smaller part of overall spatial variability; it has medium spatial autocorrelation when 25% = < C0/(C + C0) < = 75%; while C0/(C + C0) >75%, it has weak autocorrelation. Among the 8 elements, random factors of W.S.S. B take up the smallest part with the ratio of 10.7%, which indicates that random factors have less influence on it while internal factors have more. Then it’s Effect. Mo and Effect. Cu etc., occupying 56.9%, 70%, 72.2%, 81.9%, 83.8%, 90.8% relatively; R-Avail. K has the maximum of spatial random variability, and its value of C0/(C + C0) is 93.1%.
Range represents the spatial autocorrelation scope of soil nutrients. The greater the range, the larger the spatial autocorrelation scope; conversely, it’s the same. In the 8 elements, range of Org. C that has the largest spatial autocorrelation scope is greatest, while the smallest is Effect. Cu.
Spatial variability of different soil nutrients changes much, and their fitted models are varied. From Table 4, it can be seen that coefficient of determination of Effect. Zn is 0.126, the smallest, with the minimum fitting characteristics which indicates that the element is unsuitable for overall regional fitting; while Org. C has the largest coefficient of determination, 0.984.
5. Conclusions and Discussion
Discrete degree of content of the 8 soil elements is high. The values of coefficient of variation of Org. C, Total N, R-Avail. K, Effect. Mo, Effect. Zn, Effect. Cu and W.S.S. B are 0.3777, 0.2972, 0.5236, 0.6848, 0.748, 0.5035 and 0.6223 relatively, and they all belong to medium variability. Coefficient of variation of effective phosphorus with the strongest variability is 0.9999, and the largest. The reason why the high discrete degree of content of the elements exits is that Han River has an influence on the distribution of soil nutrients and leads to litter relevance of different parts of Zhongxiang integrated as a whole.
1) There is a trend about the patterns of coefficient of variation for most elements horizontally. For example, Org. C has a medium spatial variability both in the plain and downland in the east of Han River, that is, the spatial variability from west to east in east Zhongxiang is consistent; and it’s the same from east to west in west Zhongxiang (see Table 5). It seems that the characteristics of coefficient of variation have nothing to do with the terrains. However, differences will appear when the same terrains that have some distances to each other are integrated. When east plain and west plain are integrated as a whole, the spatial variability is medium, while it is strong if east downland and west downland are integrated. The only difference of two integrated styles is the distance between the two objects before they integrated. It also can be seen from Figure 2 that the distance between east plain and west plain is shorter than that between east downland and west downland. This just proves the previous assumption. Not only does that pattern suits Org. C, but also R-Avail. K, Effect. Mo, Effect. Zn, Effect. Cu and W.S.S. B do.
2) The same element has different variability in different areas. For example, Org. C has strong variability in the downland while having medium variability in other areas (see Table 5). It is a similar trend for nutrients like Total N, R-Avail. K, Effect. Mo, Effect. Zn,
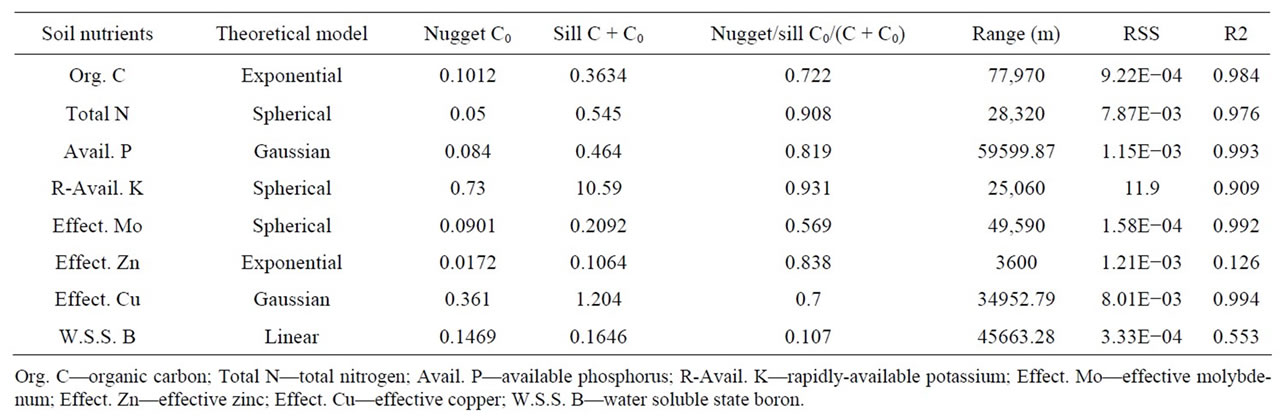
Table 4. Results of spatial structural analysis.
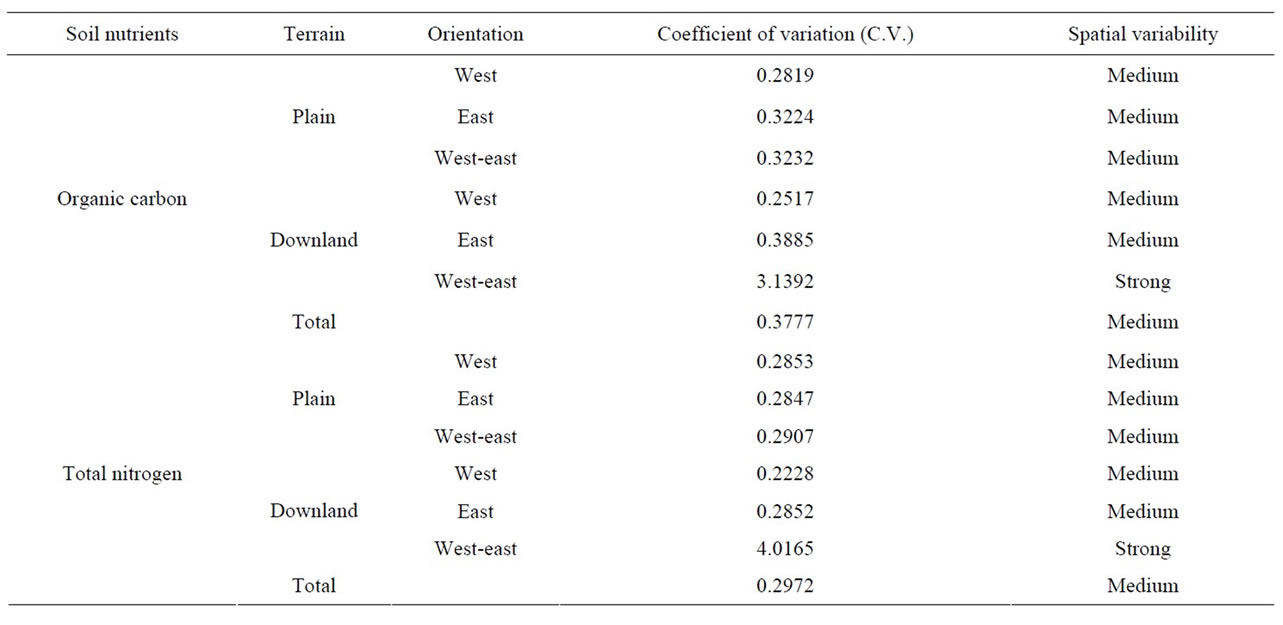
Table 5. Spatial variability of organic carbon and availability in the different areas of Zhongxiang.
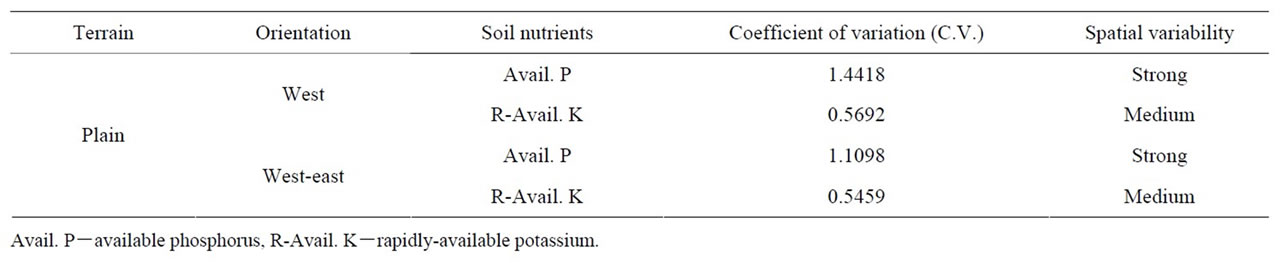
Table 6. Variability of available phosphorus and rapidly-available potassium.

Table 7. Spatial autocorrelation of organic carbon in different areas of Zhongxiang.
Effect. Cu and W.S.S. B.
3) Different elements have similar spatial variability in the corresponding terrain areas in Zhongxiang. Take Org. C and Total N as an example (see Table 5).
In Table 5, it’ clear that C.V. of Org. C and Total N in the downland is more than 1 and they own strong variability, while it’s medium variability in other areas where the C.V. value is between 0.1 and 1. Not only do Org. C and Total N have such characteristics, but also R-Avail. K, Effect. Mo, Effect. Zn, Effect. Cu and W.S.S. B do.
4) Different elements have different spatial variabilities in the same terrain of the same orientation. Take Avail. P and R-Avail. K as an example (see Table 6). From the table, it can be seen that Avail. P has strong variability while R-Avail. K possesses medium variability in the plain of west Zhongxiang. Similarly, available potassium has strong variability while R-Avail. K possesses medium variability.
5) In terms of theoretical fitted model of the 8 elements, spherical model to which Total N, R-Avail. K and Effect. Mo belong occupies the biggest part, amounting to 37.5%. Exponential model and Gaussian model, which Org. C and Effect. Zn, Avail. P and Effect. Cu pertain to relatively, both take up 25%. The last element, W.S.S. B, fits linear model accounting for 12.5%.
6) The variability caused by random factors takes up a larger part of the overall spatial variability. Ratio of nugget to sill C0/(C + C0) of Total N, effective phosphorus, R-Avail. K and Effect. Zn is 0.908, 0.819, 0.931 and 0.838 separately and they all have weak spatial autocorrelation. The values of C0/(C + C0) of Org. C, Effect. Mo and Effect. Cu are 0.722, 0.569 and 0.7 respectively and they have medium spatial autocorrelation. However, W.S.S. B possesses strong spatial autocorrelation.
7) Ratio of random variability of the same element to overall spatial autocorrelation is different in the different areas. Take Org. C as an example (see Table 7).
It can be concluded that ratio of random variability of Org. C to overall spatial variability is 50.2%, 84.7%, 57.7%, 68.9%, 87.6%, 53.0% and 72.2% respectively in the plain of west Zhongxiang, plain of east Zhongxiang, downland of west Zhongxiang, downland of east Zhongxiang and Zhongxiang. Therefore it’s weak spatial autocorrelation in the plain of east Zhongxiang and downland of east Zhongxiang, while it’s medium spatial autocorrelation in other areas.
REFERENCES
- X. W. Zhou, X. M. Zhao, G. R. Hu, F. H. Chen and X. Guo, “The Analysis of Soil Nutirent Variability in the Hilly Paddy Field of Southern China,” Acta Argriculturae Universitatis Jiangxiensis, Vol. 31, No. 5, 2009, pp. 919- 926.
- Y. L. Wang, Y. H Miao, J. F. Tan and Y. L. Han, “Analyzing on Soil Nutrient and Fertilization Conditions in the North Plain of Henan Province,” Chinese Agriculture Science Bulletin (Soil and Fertilizer Science), Vol. 24, No. 10, 2008, pp. 296-299.
- T. L. Mu and Q. J. Wang, “Soil Water and Nutrient Loss Characteristics in a Small Watershed of Hilly Region of Loess Plateau,” Journal of North University of China (Natural Science Edition), Vol. 28, No. 4, 2007, pp. 349- 355.
- J. P. Liu, Z. W. Chen, H. X. Wang and X. L. Li, “Study on Spatial Variability of Soil Nutrients in the Precision Agriculture Hardcore Demonstration Plot of Jilin Province,” Journal of Jilin Normal University (Natural Science Edition), Vol. 28, No. 3, 2007, pp. 74-84.
- J. C. Wu, Z. T. Gong, Z. Y. Wang, C. L. Kou and Z. J. Yang, “Study on Characteristics of Soil Nutrients in Temporal and Spatial Changing and Its Utilization in the East of Henan Province,” Soil and Environmental Sciences, Vol. 9, No. 3, 2000, pp. 227-230.
- L. P. Yang and J. Y. Jin, “Study on Soil Fertility Variability and Evaluation Using Sampling Technique in Field of the Plain Area,” Soil and Fertility, Vol. 1, No. 2, 2001, pp. 8-13.
- J. Wang, B. J. Fu, Y. Qiu, L. D. Chen and L. Yu, “Spatial Heterogeneity of Soil Nutrients in a Small Catchment of the Loess Plateau,” Acta Ecological Sinica, Vol. 22, No.8, 2002, pp.1173-1178.
- M. Zhang, “Spatio-Temporal Variability Study of Soil Nutrients Based on GIS and Geostatistics,” M.A. Dissertation, Henan Agricultural University, Zhengzhou, 2010.
- J. Yu, “Spatial Variability and Its Application of Soil Nutrients Based on GIS and Geostatistics,” Ph.D. Dissertation, Huazhong Agricultural University, Wuhan, 2007.
- W. N. Tan, Z. A. Li, B. Zou and Y. Z. Ding, “The Application of Geostatistics to Soil Science,” Tropical Geography, Vol. 25, No. 4, 2005, pp. 307-311.
- Y. Li, Z. Shi, J. M. Xu and M. X. Huang, “Utilization and Perspective of Geostatistics in Soil Science,” Journal of Soil and Water Conservation, Vol. 17, No. 1, 2003, pp. 178-182.
- D. McGrath, C. S. Zhang and O. T. Carton, “Geostatistical Analyses and Hazard Assessment on Soil Lead in Silvermines Area, Ireland,” Environmental Pollution, Vol. 127, No. 2, 2004, pp. 239-248. doi:10.1016/j.envpol.2003.07.002

