Open Journal of Modern Hydrology
Vol.05 No.02(2015), Article ID:56031,12 pages
10.4236/ojmh.2015.52004
Groundwater Leakage and River Runoff in a Catchment Influenced by Tectonic Movement
Md Motaleb Hossain1, Kazuhisa A. Chikita2*, Yoshitaka Sakata2, Takuto Miyamoto1, Yasuhiro Ochiai1
1Graduate School of Science, Hokkaido University, Sapporo, Japan
2Faculty of Science, Hokkaido University, Sapporo, Japan
Email: *chikita@mail.sci.hokudai.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 March 2015; accepted 27 April 2015; published 29 April 2015
ABSTRACT
In order to clarify how groundwater leakage and river runoff occur in a catchment under tectonic movement, the water balance was estimated in the forested (88.3% in area) Oikamanai River catchment (area, 62.6 km2), Hokkaido, Japan. The catchment’s geology is early Miocene to Pliocene sedimentary bedrock of partly high permeability, accompanied by currently active faults. Daily evapotranspiration, E, in water balance was calculated by applying the one-layer model to meteorological data in the rainfall season of 2011 and 2012, with the topographic influence on heat balance of the catchment considered. The coupling with the short-term water balance method for river runoff events allows us to estimate groundwater leaking to the other catchments through the faults and bedrock. As a result, the leakage corresponded to 50% - 80% of effective rainfall (=P − E: P, rainfall) in 2011, whereas it was lower or negative in 2012. The estimate of leakage then included variability of ca. 80%. In 2012, shallow groundwater storage seems to retain high baseflow during non-rainfall.
Keywords:
Groundwater Leakage, Fault, Water Balance, Evapotranspiration, One-Layer Model

1. Introduction
Focusing on the forest and land management and the water resource assessment on the time scale of one to 100 years order, it is important to know how the water balance is built up in a forested catchment and consequently the river runoffs occur. For estimating the water balance in the catchment, it is necessary to reasonably evaluate actual evapotranspiration, groundwater storage change, and groundwater leakage to the other catchments or coastal regions. With respect to the groundwater storage and leakage, there are many hydrogeological studies of groundwater flow system in bedrocks with fractures or faults [1] -[4] . These focus on the hydrological role of fractures or faults in groundwater flow system. There are some studies of interactions between surface water and groundwater. Wang et al. [5] investigated the dynamics of surface water leaking to groundwater, while Modica et al. [6] and Sakata & Ikeda [7] explored the seepage of unconfined groundwater to river water on the scale of catchment or an alluvial fan. These studies are all related to water resource assessment on monthly to inter-annual basis. However, there are few studies on interaction between river water and groundwater on catchment scale, accompanied by faults. In such a geologically active catchment, it is unknown how rainfall or snowmelt runoff events are related to groundwater storage and leakage to deeper zone.
The groundwater flow in a catchment or region of 102 to 105 km2 order has been explored on the monthly to annual scale by welling observations and providing some models such as MODFLOW [8] , Hydro Geo Sphere (HGS) [9] , Integrated Water Flow Model (IWFM) [10] , etc. with the internal structure of sedimentary deposits or bedrocks. The stream flow is taken into account as part interacting with groundwater in these groundwater models [11] . The models of interaction between surface water and groundwater on the monthly to annual scale have been also designed by Hughes [12] [13] and Hughes et al. [14] .
In this study, water balance in the geologically active and forested (88.3% area) Oikomanai River catchment, Hokkaido, Japan, is estimated on a daily basis, and how effective rainfall produces groundwater leakage and storage in the catchment is explored.
2. Materials and Methods
2.1. The Study Area
The Oikamanai River is a main influent river of the Oikamanai Lagoon in the Tokachi coastal region of southeastern Hokkaido, Japan (Figure 1; [15] [16] ). The river catchment (42˚33'46'' to 42˚40'40''N, 143˚21'47'' to
Figure 1. Location of the Oikamanai River catchment (DEM) and observation sites. The land use map of the catchment is also shown.
143˚28'36''E; altitude, 6 m to 330 m asl) upstream of site R1 has the area of 62.6 km2, the mean slope angle of 34.7˚ (gradient, 0.692) and the mean riverbed gradient of 0.033 (Figure 1). The distribution of slope angle corresponds to that of the surface geology (Figure 2); the upper, middle and lower regions with relatively steep slope in the northwest to southeast directions are occupied by sedimentary rocks of early to middle Miocene, middle to late Miocene and late Miocene to Pliocene, respectively, and the lowest region with relatively gentle slope just upstream of site R1 by alluvial flood deposits. The sedimentary rocks are composed of conglomerate, sandstone, mudstone, siltstone and tuff, of which the former two exhibit high permeability. The sedimentary rocks in the mountainous regions are accompanied by many faults, which are due to the orogenic movement of the Hidaka Range in Miocene to Pliocene, west of the river catchment. The northern faults are currently active, being adjacent to the Tokachi Median Tectonic Zone to north [17] . The faults tend to frequently produce landslides or collapse in the mountainous region (Tokachi Subprefecture HP; URL: http://www.tokachi.pref.hokkaido.lg.jp/sr/srs/gaiyou/sugata/sugata.htm) (Figure 2). The relatively young sedimentary rocks of Miocene to Pliocene with faults could also leak some groundwater to the other catchments or to the Pacific Ocean. Pyroclastic deposits, loam, sand and gravel in late Pleistocene are distributed along the border of flood plain (Figure 2) and in forest soils. Such porous deposits could make the seepage easy from the forest region to the flood plain.
The catchment upstream of site R1 is covered by 88.3% forest in the mountainous region, 10.6% farmland (mostly, grassland) on the lowest alluvial plain, etc. (Figure 1). The forest is composed of ca. 50% broad-lea- ved and ca. 50% coniferous (mainly, Sakhalin fir; Abies sachalinensis) trees.
2.2. Data Collection
River stage at site R1 was recorded at 30 min intervals by an air pressure logger and an air pressure-plus-water pressure logger with temperature sensors (HOBO U20, Onset Computer, Inc., USA; the range of 69 - 207 kPa and the accuracy of ±0.62 kPa for pressure, and the range of −20˚C to 50˚C and the accuracy of ±0.2˚C for temperature). The water pressure logger was set at near the deepest point in the cross-section of site R1 in Novem-
Figure 2. Geologic map of the catchment.
ber 2010. The water level, h (m), at site R1 was changed into river discharge, Q (m3/s), by the h-Q rating curve (Q = 11.72h1.373, R2 = 0.966, P < 0.01). The rating curve was obtained by frequent discharge measurements in April-November of 2011 and 2012 during the stage recording. River discharge was calculated by measuring the depth averaged velocity at about 20 sections partitioned in the cross-section and then summing the sectional discharge defined by the product of the sectional area. Then, the unchanged positions of the two loggers were ascertained by frequent surveys with three benchmarks. The Oikamanai River is frozen in December-March, when the h-Q rating curve is not applicable. Hence, the discharge obtained in the non-frozen season of April-November is applied for discussing the characteristics of discharge. For estimating water balance of the catchment, discharge and meteorological data in the rainfall season in the catchment of no snow cover are utilized, because the snow-covered period in April is very short (about two weeks).
Meteorological data were obtained at site M (altitude, 6 m asl; rainfall and air temperature) near the Oikamanai Lagoon [15] [16] at 4.0 km south-southeast of site R1, at site P (altitude, 142 m asl; rainfall and air temperature) near the water divide of the Oikamanai catchment, at site F (altitude, 34 m asl; air temperature, relative humidity and rainfall) (Figure 1), and at the Taiki Aerospace Research Field (altitude, 21 m asl; rainfall, air temperature, solar radiation, and wind velocity) 10.5 km south-southwest of site R1, and at Taiki town (altitude, 85 m asl; snow depth, rainfall, air temperature, and wind velocity) 18.9 km southwest of site R1. The distinction between rainfall and snowfall in the catchment was made by the air temperature of 0˚C at site M.
Dates for the start and end of snow cover within the catchment were suggested by using the RGB images of MODIS/Terra or MODIS/Aqua with the resolution of 500 m (URL: http://www.eorc.jaxa.jp/cgi-bin/adeos/modis_frame.cgi?year=2014&month=10&prov=eoc&type=500mchla) and snow depth data at Taiki town. Considering a topographic effect on the solar radiation, the DEM in Figure 1 was applied to know the slope angle and aspect of the basin. The elevation effect on rainfall was explored by using the rainfall data at site M, site F and site P, and analytical rainfall data of 1 km × 1 km mesh by the Japan Meteorological Agency. The mesh data are built up at 1 h intervals by coupling in situ rainfall with radar echo, and the mesh covers the main Japanese islands (Hokkaido, Honshu, Shikoku, Kyushu, etc.) (URL: http://www.jma.go.jp/jma/jma-eng/jma-center/nwp/outline2013-nwp/index.htm).
3. Results and Discussion
Figure 3 shows hourly time series of discharge and water temperature at site R1, air temperature and precipitation at the Taiki Aerospace Research Field, and snow depth at Taiki town in March or April 2011-November 2012. As a result, each total rainfall amount in 2011 and 2012 indicated the difference of less than about 10% among the two meteorological stations in Figure 3, and site M and site P in the catchment (Figure 1). For the period of 6 December 2011-30 March 2012, the water temperature held at less than 0˚C. The water pressure logger was then located at ca. 40 cm above the riverbed. The Oikamanai River at site R1 was thus completely frozen at the height more than ca. 40 cm above the deepest riverbed. The rating curve of Q = 11.72h1.373 was then not applicable at site R1, because the covered-ice growth and snow accumulation on the ice substantially increased the water pressure recorded. As a result, the accurate observation of snowmelt river runoffs in the early snowmelt season of March was difficult, because the melt water then flowed on the covered ice. The rainfall runoff events with mean runoff rate of 0.1 mm/h (mean discharge of 1.75 m3/s) or more at site R1 were recorded 29 times in April to November of 2011 (12 events) and 2012 (17 events) (Table 1). The largest runoff event over the periods occurred by a heavy rainfall (totally, 221 mm for 2000 h on 3 May to 0200 h on 5 May) immediately after the snowmelt season. The peak discharge of the largest runoff event was 36.4 m3/s at 1400 h on 4 May 2012.
The baseflow after the snowmelt season of 2012 was consistently high compared with that in 2011 (Figure 3). This is probably due to the high and long groundwater storage by relatively large snowmelt in March 2011 and the subsequent largest runoff event in early May. With respect to the snowmelt, the initial positive daily mean air temperature of 2011 and 2012 at the Taiki Aerospace Research Field and Taiki town was recorded on 13 March (2˚C) and 30 March (7.5˚C), respectively, when the snow depth at Taiki town was at 40 cm and 73 cm, respectively. Thereafter, covered snow in the catchment or around disappeared on 30 March 2011 and 19 April 2012. Calculation of the snowmelt amount by the degree-day approach [18] indicated that the snowmelt amount in 2012 was two times as large as that in 2011.
The ratio of runoff rate to total rainfall for the runoff events in Table 1 exhibits a wide range of 5.9% to
Table 1. Discharge, total rainfall, runoff rate and ratio of total runoff rate to total rainfall for rainfall runoff events at mean runoff rate of more than 0.1 mm/h in 2011 and 2012.
*composite of two sequential runoff events, runoff events utilized for the short-term water balance method.
160.5%. The very high ratios of 160.5% and 148.7% were recorded for the No. 7 and No. 27 runoff events of 5 - 8 September 2011 and 12 - 15 November 2012, respectively. Meanwhile, the other events have the ratios of 5.9% - 26.2 % in 2011 and 9.4% - 41.8% in 2012. This suggests that high groundwater storage in the catchment sporadically produces relatively large discharge.
4. Water Balance of the Catchment
4.1. Preparation for Calculation
The time series of discharge and meteorology in Figure 3 and meteorology at site M, site F and site P are utilized as a daily data base for calculating water balance of the Oikamanai River catchment. This calculation is needed for estimating the groundwater leakage to the other catchments or the Pacific Ocean, and simulating the hydrographs at site R1. The accuracy in discharge is relatively very low in the frozen period, and the daily spatial change of snow depth in the catchment in the snowmelt season is unknown. Hence, the frozen and snowmelt seasons are excluded for the calculation.
The DEM and land-use maps of the catchment in Figure 1 were utilized for evapotranspiration calculation, because effects of slope angle, slope aspect and surface condition on the solar radiation should be considered. Figure 4 shows spatial distributions of slope angle and aspect in the catchment (resolution, 0.1 km). As a result, the averaged slope angle and aspect were 34.66˚ and 176.6˚ (clockwise from north at 0˚), respectively. The basin slope thus faces almost south on average. With respect to land use, each value of albedo α and dimensionless bulk transfer coefficient of sensible heat CH was considered for forest and grassland separately.
Water balance of a catchment for a certain period is given as follows:
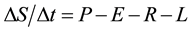 (1)
(1)
where ΔS is groundwater storage change (mm) for the water-balance period Δt (day), P is precipitation (mm/d), E is evapotranspiration (mm/d), R is runoff rate (mm/d) at the “exit” of the catchment (here, site R1 in Figure 1),
Figure 3. Hourly time series of discharge and water temperature at site R1, air temperature and precipitation at the Taiki Aerospace Research Field, and snow depth at Taiki town.
Figure 4. Spatial distributions of slope’s (a) angle and (b) aspect in the catchment with 0.1 km resolution.
and L is groundwater leakage (mm/d). The runoff rate, R, is calculated from daily discharge (m3/d) divided by the catchment area (6.26 × 107 m2). Here, the evapotranspiration, E, is calculated by the one-layer model for the forest or grassland area (Figure 1). In the one-layer model, the leaf-surface temperature, Te (K), at a certain height in forest or grassland is obtained by the successive approximation method to satisfy the following heat balance equations:
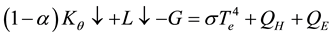 (2)
(2)
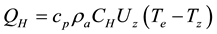 (3)
(3)
 (4)
(4)
where Kθ↓ is downward shortwave radiation (W/m2) onto the catchment of slope angle θ, α is albedo, L↓ is downward long wave radiation (W/m2), G is soil heat flux (W/m2), σ is the Stefan-Bolzmann constant (=5.670 × 10−8 W/m2/K4), QH is sensible heat flux (W/m2), QE is latent heat flux (W/m2), λ is vaporization heat (J/kg), cp is specific heat (J/kg/K) of water at constant pressure, ρa is air density (~1.2 kg/m3), ε is the ratio of water vapor density to dry air density (=0.622), CH is a dimensionless bulk transfer coefficient for sensible heat flux, Tz is air temperature (K) at z, uz is wind speed (m/s) at the height, z, above the earth surface, p is air pressure (Pa) at z, ez is the vapor pressure (Pa) at z, e0(Te) is saturated vapor pressure (hPa) at leaf-surface temperature Te, and β is evaporation efficiency (=CE/CH; CE, dimensionless bulk transfer coefficient for latent heat flux).
Here, the albedo α is supposed to be constant at 0.10 or 0.15 for the forested (88.3% area) Oikamanai River catchment, since α = 0.05 - 0.15 for broadleaf forest, α = 0.1 - 0.2 for needleleaf forest and α = 0.15 - 0.25 for grassland (Figure 1; [19] ). Actually, considering these ranges and the ratio of the land use area in Figure 1, the α value can be 0.08 - 0.18. The evaporation efficiency β is given at 0.3 for Equations (3) and (4), because β = 0.26 at the mixed broadleaf and needle leaf forest in summer [20] . When rainfalls at site M and site P was more than 40 mm/d, and relative humidity at site F was 100%, β = 1 was given. The bulk transfer coefficient, CH, for sensible heat flux is assumed to range from 0.005 to 0.008 for forest and grassland.
Downward shortwave radiation Kθ↓onto the basin slope is calculated by the following equations [21] :
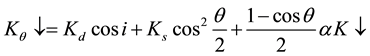 (5)
(5)
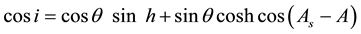 (6)
(6)
where Kd is direct shortwave radiation onto a normal surface, Ks is scattered shortwave radiation onto a plane, K↓ = Kd sinh + Ks, i is an incident angle of shortwave radiation onto the slope, h is solar elevation, As is solar azimuth, and A is slope aspect (clockwise from A = 0˚ for the south-facing slope). Kd and Ks in Equation (5) were obtained by the following equations.
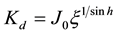 (7)
(7)
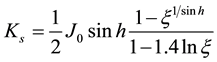 (8)
(8)
where J0 is the solar constant (=1353 W/m2 as annual average), ζ is atmospheric transmissivity, and here is assumed to be constant at 0.7. The downward shortwave radiation Kθ↓ onto basin slope was calculated by using hourly K↓ data (θ = 0˚) at the Taiki Aerospace Research Field. Here, Kθ↓ in Equation (5) was calculated at θ = 34.66˚ (averaged slope angle) and A = 356.6˚ (averaged slope aspect) (Figure 4).
Daily mean values (Ld↓) of downward long wave radiation L↓ in Equation (2) were calculated by the following equations [20] :
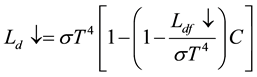 (9)
(9)
 (10)
(10)
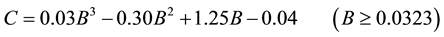 (11)
(11)

where B = Kd ↓/Kdf ↓ (Kd ↓and Kdf ↓, daily mean shortwave radiation observed on the plane and in fair weather, respectively), Ldf ↓ is daily mean longwave radiation in fair weather, and T is daily mean air temperature (K) at z. C is a factor of cloud effect with C = 1 in fair weather. Ldf ↓ is calculated as follows:


where w is total amount (cm) of effective water vapor, and Tdew is daily mean dew point temperature (˚C) at z, respectively. Daily mean shortwave radiation Kdf↓ in fair weather is calculated by using a relation with daily mean downward shortwave radiation K0d↓on a horizontal surface in the upper end of atmosphere [20] .
When Equations (2)-(4) are applied at the daily base, the soil heat flux G could then be negligibly small compared with the other heat fluxes. Here, the daily mean Kθ↓ calculated and the wind speed, U10 (Uz at z = 10 m) at the Taiki Aerospace Research Field, and daily mean air temperature and relative humidity at site F are adopted to obtain daily mean T10 and e10 values and the Tdew values at z = 10 m. Then, for daily mean air temperature, its spatial distribution or the elevation effect in the catchment should be taken into account. However, the daily mean air temperature at sites M, R1, F and P (Figure 1) did not indicate such a clear environmental lapse rate as −0.65˚C/100m, and the difference of the daily air temperature was abs(ΔT) < 0.5℃ between site F and the other sites. This is probably due to the usual prevalence of sea wind from the Pacific Ocean (Figure 1). Finally, the Te value obtained by the successive approximation method yields:


where ρw is water density (kg/m3) at Te, and E is evapotranspiration (mm/day).
The groundwater leakage, L, in Equation (1) is estimated, since the catchment has many faults in addition to the relatively porous sedimentary bedrock (Figure 2). The (E + L) in Equation (1) is obtained by the short-term water balance method, where a time period covering one or more rainfall runoff events (Table 1) is adopted to satisfy Qt1 = Qt2 for river discharge at the initial time t1, and the final time t2 (Figure 5). In the method, it is assumed that the groundwater storage occurs at any time in the same underground zone. Then, the river discharge Q corresponding to the baseflow is proportional to groundwater storage, S, and ΔS = 0 at between t1 and t2. Here, mean daily rainfall, P, at site P and mean daily runoff rate, R, at site R1 over a time period giving ΔS = 0 (Figure 1), and mean daily evapotranspiration, E, for the days nearly equal to the time period are applied to Equation (1) to numerically obtain the leakage L. A spatial distribution of the daily rainfall in the catchment should then be considered.
Figure 6 shows four examples of daily rainfall distributed in the catchment. These plots are based on the analytical rainfall data of 1 km × 1 km mesh by the Japan Meteorological Agency. The statistical F-test was performed for the slopes in the linear models for rainfalls of more than 10 mm/d. As a result, the hypothesis of no trend was rejected for the rainfalls. However, the correlation was consistently small (R2 < 0.2) as in Figure 6. Hence, the elevation effect on rainfalls is almost negligible in this catchment. The utility of the rainfall data at site P (142 m asl in altitude) can thus be reasonable for estimating the leakage.
Figure 5. Example of application of the short-term water balance method to rainfall runoff events (here, No. 9 and No. 10 events in Table 1).
Figure 6. Relations between the elevation and daily rainfall in the catchment.
4.2. Calculated Results
Actual evapotranspiration E evaluated by the one-layer model (α = 0.1, CH = 0.008), the daily rainfall P at site P and the runoff rate R at site R1 are shown in Figure 7. The evapotranspiration E in the rainfall season of 12 April-30 November 2011 and 20 April-30 November 2012 was calculated using the shortwave radiation at θ = 34.66˚ and A = 356.6˚. As a result, Total E, P and R over the periods were 348.1 mm, 971.5 mm and 418.4 mm for 2011, and 324.4 mm, 1039.5 mm and 839.1 mm for 2012, respectively. Calculated shortwave radiation Kθ↓ onto the basin slope of θ = 34.66˚ and A = 356.6˚ was by 24% larger than the solar radiation K↓ at the Taiki Aerospace Research Field, and consequently actual evapotranspiration increased by 33% and 30% in 2011 and 2012, respectively, compared with that from the K↓ values. For a period of 1 May-31 October with no snow cover in the catchment, total E, P and Rare 296.2 mm, 815.5 mm and 325.7 mm for 2011, and 290.6 mm, 797.5 mm and 609.3 mm for 2012, respectively. Potential evapotranspiration, PE, by the Hamon method [22] indicates 428.5 mm and 438.6 mm for 1 May-31 October of 2011 and 2012, respectively. The evapotranspiration ratio E/PE is thus given at 0.69 and 0.66 in 2011 and 2012, respectively. These values are reasonable to calculated results, E/PE = 0.65, in the upper Ishikari River catchment, Hokkaido [23] . The E, P and R values averaged over 1 May-31 October are 1.61 mm/d, 4.43 mm/d and 1.77 mm/d for 2011, and 1.58 mm/d, 4.33 mm/d and 3.31 mm/d for 2012, respectively. Thus, in the non-snow-covered season, the runoff rate R corresponds to 40% and 76% of P for 2011 and 2012, respectively. The ratio of R/(P ? E) is then 0.63 and 1.20 for 2011 and 2012. The great difference of the R/(P ? E) ratio suggests that the groundwater storage, contributing to river discharge, greatly changes year by year. After the snowmelt in April 2012, the runoff rate during non-rainfall was consistently higher than that in 2011 (Figure 3) and the E values in 2012 (Figure 7). This causes the R/(P ? E) ratio to be more than unity in 2012. This suggests that in addition to the groundwater storage by snowmelt in April, large groundwater storage was produced by the heavy rainfall in early May (total rainfall, 221 mm in Table 1).
Figure 7. Daily evapotranspiration calculated by the one-layer model, rainfall at site P, and runoff rate at site R1. (a) 2011; (b) 2012.
Relations between the leakage, L, and the effective rainfall (or infiltration), (P ? E), are shown in Figure 8. As a result, for the application of the short-term water balance method to the (E + L) estimate, 20 time periods with the duration of 38 to 649 hrs (14 and 6 time periods in 2011 and 2012, respectively) were selected. Each of all the time periods covered the period of one or more rainfall events (Figure 5). In 2012, relatively small runoff events for the 6 time periods (Table 1) were suitable for the application. In 2011 (white circles in Figure 8), it is evident that the groundwater leakage to the other catchments linearly increases with the effective rainfall. The groundwater leakage then occupies ca. 50% - 75% of the effective rainfall, but, when (P ? E) is 1.3 mm/d or less, the leakage is nearly zero or a little negative. The large leakage is likely due to the young sedimentary bedrocks with many faults (Figure 2), where the deep percolation of rainwater prevails. Such large deep percolation could be connected to the restraint of river flood in the catchment. In 2012 (black circles in Figure 8), the leakage is negative for the 4 time periods, when the effective rainfall is less than 2.1 mm/d.
The application of the short-term water balance method in 2012 was limited to the small effective rainfalls, and the leakage was then negative for the 4 time periods. The negative values are probably due to large variability of the actual evapotranspiration estimated and the relatively high runoff rate during non-rainfall in 2012 (Figure 7(b)), as reflected by R/(P ? E) = 1.20 averaged over 1 May-31 October. For small runoff events, the leakage from the short-term water balance method seems to partially exclude discharge from the relatively large groundwater storage. For modelling discharge time series of the Oikamanai River, it is important to consider if the leakage and groundwater storage is considerably large or not.
5. Variability and Uncertainty
The downward shortwave radiation onto slope angle θ = 34.66˚ (mean μ) averaged over the catchment was by 24% larger than that at the Taiki Aerospace Research Field. Consequently the actual evapotranspiration E increased by 29% and 23% in 2011 and 2012, respectively (Figure 7). The spatial distribution of catchment slope angle in Figure 4(a) has the standard deviation σ of 24.20˚. Thus, downward shortwave radiation at slope aspect A = 356.6˚ was calculated at between θ = 10.46˚ (=μ ? σ) and θ = 58.86˚ (=μ + σ) As a result, compared with downward shortwave radiation at θ = 34.66˚, it gradually decreased to the ratios of 0.85 and 0.79 at θ = 10.46˚ and 58.86°, respectively, which is comparable in magnitude to the downward shortwave radiation onto a plane. Thus, the E value from Kθ↓ at θ = 34.66˚ proves to be nearly maximum.
The catchment slope aspect A takes μ = 356.6˚ (almost southward) and σ = 79.0˚ (Figure 4(b)). For the E calculation, ranges of 277.6˚ ≤ A < 360˚ and 0° ≤ A ≤ 75.6˚ were applied to Equation (6) at θ = 34.66˚. Consequently, downward shortwave radiation at A = 356.6˚ decreased to the ratios of 0.926 and 0.774 at A = 75.6˚ (nearly west-southwestward) and 277.6˚ (almost eastward), respectively. Thus, the Kθ↓ at θ = 34.66˚ and A =
Figure 8. Relations between the effective rainfall and the calculated groundwater leakage in 2011(white circles) and 2012 (black circles).
356.6˚ offers a nearly peaked E. In contrast, the Kθ↓ at θ = 58.86˚ and A = 277.6˚ may be smallest at ca. 47% of the Kθ↓ values at θ = 34.66˚ and A = 356.6˚, and total E values at θ = 34.66˚ and A = 356.6˚ decreased by ca. 61%. Then, total E values at the albedo α = 0.1 for 12 April-31 November 2011 and 20 April-30 November 2012 were by 0.5% smaller and by 7.0% larger than those at α = 0.15, respectively. Thus, the difference of the albedo does not greatly influence actual evapotranspiration from the catchment.
It was found that actual evapotranspiration estimated by the one-layer model varies mainly by the angle and aspect of the catchment slope. Then, there is the variability of decreasing up to ca. 61% from nearly peaked E. The standard deviation of rainfall P in the catchment is within 15% at less than 100 mm/d (Figure 6), and an observation error of runoff rate R at site R1 is within 10%. As a result, the effective rainfall, P − E, and the leakage, L (= P − E − R), in Figure 8 have variability of ca. 80%, respectively. The negative L values at the small effective rainfalls of 2012 could thus be regarded as almost zero.
6. Conclusion and Future Work
The characteristics of discharge were specified in the geologically active and forested Oikamanai River catchment using data sets obtained in the rainfall season of 2011 and 2012, and the estimate of water balance for the catchment suggested that the groundwater leakage and storage changed inter-annually. In 2011, the groundwater leakage corresponded to ca. 50% - 75% of the effective rainfall, whereas in 2012, the leakage was negative for the 4 time periods when the short-term water balance method was applicable. The negative values were probably due to large variability of the actual evapotranspiration estimated and the relatively high runoff rate during non- rainfall in 2012. The actual leakage and storage of groundwater seem to be linked to the bedrock and faults in the catchment. The leakage estimated by water balance has the variability of ca. 80%. Thus, the inner structure and hydrological role of bedrocks and their faults should be explored by geophysical prospecting, drilling and groundwater modelling. On larger scale, studies on the submarine groundwater discharge (SGD) into the sea could be useful for ascertaining the leakage, because some catchments accompanied by sedimentary rocks with faults facing the Pacific Ocean. With respect to the forested-land management, the investigation of sediment loading processes is important, because landslides and bank collapse frequently occur due to the active tectonic movement. As a next step, a model for simulating river runoff and sediment load will be proposed.
Acknowledgements
We are indebted to the Taiki City Government and associated staffs for the kind permission of our field observations in the Oikamanai River catchment. We express our gratitude to the farmers, Messrs. Mori, Takahashi and Yamamori, at the Seika and Bansei Villages for the frequent water sampling and instrument management. We are also grateful to Mr. T. Usutani, Japan Weather Association, for his welcome supply of analytical rainfall data. This study was supported partly by the Grant for Joint Research Program of the Institute of Low Temperature Science, Hokkaido University.
References
- Michalski, A. and Britton, R. (1997) The Role of Bedding Fractures in the Hydrogeology of Sedimentary Bedrock― Evidence from the Newark Basin, New Jersey. Groundwater, 35, 318-327. http://dx.doi.org/10.1111/j.1745-6584.1997.tb00089.x
- Banks, D. and Robins, N. (2002) An Introduction to Groundwater in Crystalline Bedrock. Geological Survey of Norway, Trondheim, 68 p.
- Stamos, C.L., Cox, B.F., Izbicki, J.A. and Mendez, G.O. (2003) Geologic Setting, Geohydrology and Ground-Water Quality near the Helendale Fault in the Mojave River Basin, San Bernardino County, California. USGS Water-Re- sources Investigations, Sacramento, Report 03-4069, 44 p.
- Seaton, W. and Burbey, T.J. (2005) Influence of Ancient Thrust Faults on the Hydrogeology of the Blue Ridge Province. Groundwater, 43, 301-313. http://dx.doi.org/10.1111/j.1745-6584.2005.0026.x
- Wang, X.-S., Ma, M.-G., Li, X., Zhao, J., Dong, P. and Zhou, J. (2010) Groundwater Response to Leakage of Surface Water through a Thick Vadose Zone in the middle Reaches Area of Heihe River Basin, in China. Hydrology and Earth System Sciences, 14, 639-650. http://dx.doi.org/10.5194/hess-14-639-2010
- Modica, E., Buxton, H. T. and Plummer, L. N. (1998) Evaluating the Source and Residence Times of Groundwater Seepage to Streams, New Jersey Coastal Plain. Water Resources Research, 34, 2797-2810. http://dx.doi.org/10.1029/98WR02472
- Sakata, Y. and Ikeda, R. (2012) Quantification of Longitudinal River Discharge and Leakage in an Alluvial Fan by Synoptic Survey Using Handheld ADV. Journal of Japan Society of Hydrology and Water Resources, 25, 89-102. http://dx.doi.org/10.3178/jjshwr.25.89
- Harbaugh, A.W. (2005) MODFLOW-2005, U.S. Geological Survey Modular Ground-Water Model―The Groundwater Flow Process. U.S. Geological Survey Techniques and Methods 6-A16.
- Brunner, P. and Simmons, C.T. (2012) HydroGeo Sphere: A Fully Integrated, Physically Based Hydrological Model. Groundwater, 50, 170-176. http://dx.doi.org/10.1111/j.1745-6584.2011.00882.x
- Dogrul, E.C., Schmid, W., Hanson, R.T., Kadir, T. and Chung, F. (2011) Integrated Water Flow Model and Modflow- Farm Process: A Comparison of Theory, Approaches, and Features of Two Integrated Hydrologic Models. Department of Water Resources, California Natural Resources Agency, State of California, Sacramento, Technical Information Record, 70 p.
- Harter, T. and Morel-Seytoux, H. (2013) Peer Review of the IWFM, MODFLOW and HGS Model Codes: Potential for Water Management Applications in California’s Central Valley and Other Irrigated Groundwater Basins. California Water and Environmental Modeling Forum, Promoting Excellence and Consensus in Water and Environmental Modeling, Sacramento, August 2013, 121 p.
- Hughes, D.A. (2004) Incorporating Groundwater Recharge and Discharge Functions into an Existing Monthly Rainfall- Runoff Model. Hydrological Science Journal, 49, 297-311. http://dx.doi.org/10.1623/hysj.49.2.297.34834
- Hughes, D.A. (2009) Simulating the Hydrology and Total Dissolved Solids (TDS) of Ephemeral Rivers in South Africa for Environmental Water Requirement Determinations. River Research and Applications, 25, 850-860. http://dx.doi.org/10.1002/rra.1188
- Hughes, D.A., Kapangaziwiri, E. and Baker, K. (2010) Initial Evaluation of a Simple Coupled Surface and Ground Water Hydrological Model to Assess Sustainable Ground Water Abstractions at the Regional Scale. Hydrology Research, 41, 1-12. http://dx.doi.org/10.2166/nh.2010.038
- Chikita, K.A., Iwasaka, W., Mamun, A.A., Ohmori, K. and Itoh, Y. (2012) The Role of Groundwater Outflow in the Water Cycle of a Coastal Lagoon Sporadically Opening to the Ocean. Journal of Hydrology, 464-465, 423-430. http://dx.doi.org/10.1016/j.jhydrol.2012.07.035
- Chikita, K.A., Uyehara, H., Mamun, A.A., Umgiesser, G., Iwasaka, W., Hossain, M.M. and Sakata, Y. (2015) Water and Heat Budgets of a Coastal Lagoon Controlled by Groundwater Outflow to the Ocean. Limnology, 16. http://dx.doi.org/10.1007/s10201-015-0449-4
- Yamaguchi, S., Sato, H. and Matsui, M. (2003) Geology in the Churui District. Quadrangle Series, 1:50,000. Kushiro (2), No. 59, 68 p.
- Braithwaite, R.J. (1995) Aerodynamic Stability and Turbulent Sensible-Heat Flux over a Melting Ice Surface, the Greenland Ice Sheet. Journal of Glaciology, 41, 562-571.
- Campbell, G.S. and Norman, J.M. (1998) An Introduction to Environmental Biophysics. Springer, New York, 286 p. http://dx.doi.org/10.1007/978-1-4612-1626-1
- Kondo, J. (1998) Meteorology in Aquatic Environments. 2nd Edition, Asakura Publication, Inc., Tokyo, 350 p.
- Tanaka, S., Takeda, H., Iwata, T., Tsuchiya, T. and Terao, M. (2006) Architectural Environmental Engineering. 3rd Edition, Inoue Publ. Inc., Tokyo, 324 p.
- Dingman, S.L. (2002) Physical Hydrology. 2nd Edition, Prentice Hall, Upper Saddle River, 646 p.
- Nakao, K. (1971) A Hydrological Study on the Stability of Water-Level of a Lake or a Swamp. Geophysical Bulletin, Hokkaido University, 25, 25-87.
NOTES
*Corresponding author.











