Open Journal of Modern Hydrology
Vol.3 No.1(2013), Article ID:27220,5 pages DOI:10.4236/ojmh.2013.31003
Streamflow Decomposition Based Integrated ANN Model
![]()
School of Mechanical and Building Sciences, VIT University, Vellore, India.
Email: roshan1979@gmail.com
Received October 10th, 2012; revised November 17th, 2012; accepted November 29th, 2012
Keywords: Artificial Neural Network; Rainfall-Runoff Modeling; Streamflow Decomposing; Black Box Modelling
ABSTRACT
The prediction of riverflows requires the understanding of rainfall-runoff process which is highly nonlinear, dynamic and complex in nature. In this research streamflow decomposition based integrated ANN (SD-ANN) model is developed to improve the efficacy rather than using a single ANN model for the flow hydrograph. The streamflows are decomposed into two states namely 1) the rise state and 2) the fall state. The rainfall-runoff data obtained from the Kolar River basin is used to test the efficacy of the proposed model when compared to feed-forward ANN model (FF-ANN). The results obtained in this study indicate that the proposed SD-ANN model outperforms the single ANN model in terms of both the statistical indices and the prediction of high flows.
1. Introduction
A wide variety of rainfall-runoff models have been developed and applied for water resources planning which is vital in terms of flood control and management. Traditionally, the hydrologists and water resources researchers have used conventional modeling techniques either deterministic models that includes physics of the underlying process or systems theoretic (black box) models. However these models require a large quantity of data and a complex methodology for its calibration. Most of the hydrological models either show unsuccessful results or become cumbersome. Many researchers report that these models fail to capture the high flows in a hydrograph [1,2] due to limited data sets available in the high flow domain (5% of total calibrating patterns) for capturing the nonlinear dynamics.
Recently the researchers have focused to decompose the data corresponding to flow hydrograph to enhance the performance of the hydrologic models. Mostly the studies have concentrated on using either the statistical techniques or soft decomposing techniques for data decomposition [3]. Studies include automated base flow separation and recession analysis [4], spectral analysis [5], wavelet transforms and runoff time series analysis [6-9], modular neural network (MNN) [10], self-organizing map (SOM) classifier [11,12] and self organizing linear output map (SOLO) [13]. Most of these studies conclude that the decomposition and partitioning of data resulted in better model performance.
Artificial neural network (ANN) has been proposed by researchers which is a system theoretic model that has gained momentum in the last few decades as it has been successfully applied to a wide range of problems in hydrology [2,14-16]. It is used to develop relationship between input and output variables using the existing data. Jain and Srinivasulu [3] proposed an integrated approach to model decomposed flow hydrograph using ANN and conceptual techniques. The streamflow decomposition was carried out based on physical processes which divide the input-output and fit the models for each of the segments [3]. However, the models developed using the distributed approach would have made the solution procedures complex significantly [3]. In this study, efforts are made to develop a simplified ANN based decomposed streamflow model without requiring any prior knowledge or understanding of physical processes. In this study the data is divided into two states namely rise and fall, based on the current state. The proposed model is compared with the feed forward ANN model, on a real case example of Kolar basin, India.
This paper is organized as follows. Section 2 provides a brief introduction on ANN. Section 3 describes proposed methodology. Section 4 illustrates the case study on Kolar basin, India. Section 5 includes Results and Discussion and the paper is concluded with summary and conclusions presented in Section 6.
2. Artificial Neural Network
The ANNs are highly interconnected mathematical models with its structure analogous to that of the human brain. It attempts to develop the massively parallel local processing and the distributed storage properties which are believed to exist in the human brain [17]. Simple processing units of an ANN are called “neurons”. Neurons having similar characteristics are grouped in one single layer (neurons in an input layer receive an input from the external source, and transmit the same to a neuron in an adjacent layer, which could either be a hidden layer or an output layer). Structure of the ANN Model is shown in Figure 1.
The general mathematical form of an ANN Model is given as:
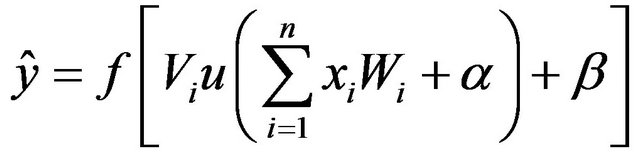 (1)
(1)
where, 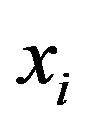 is the input of the ANN Model,
is the input of the ANN Model, 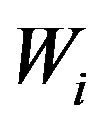 is the weight connecting input nodes to hidden nodes,
is the weight connecting input nodes to hidden nodes, 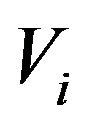 is the weight connecting hidden nodes to output nodes,
is the weight connecting hidden nodes to output nodes, 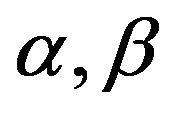 are the bias at hidden and output layer respectively and
are the bias at hidden and output layer respectively and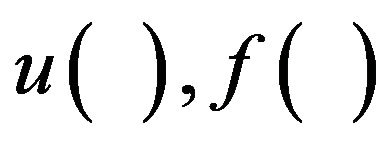 are the activation functions at hidden and output layer respectively.
are the activation functions at hidden and output layer respectively.
The weights  and
and 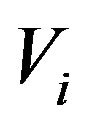 are usually determined by minimizing the quadratic error function,
are usually determined by minimizing the quadratic error function,
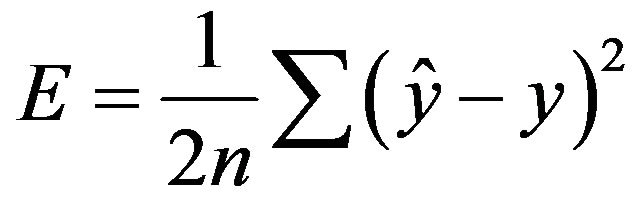 (2)
(2)
Once the ANN Model is executed then the error at the output layer from an ANN can be computed if output is known.
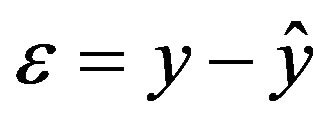 (3)
(3)
where, 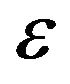 is the error at the output layer, y is the observed stream flow and y is the estimated stream flow.
is the error at the output layer, y is the observed stream flow and y is the estimated stream flow.
Using the process of the feed-forward calculations and back-propagation of the errors the connection strengths are updated and an acceptable level of output is predicted. This is called as training of an ANN. Once the network has been trained, it can be tested using the testing data.
3. Model Development
Determination of significant input variables is a very essential step in ANN Modeling [18,19]. Cross correlation is used to find the relationship between the variables [2,19-21] and is used to represent the most popular analytical techniques for selecting appropriate inputs [18]. Observed relationships between the training samples and the connection weights enhance generalization ability of an ANN model [22].
The inputs to the SD-ANN model were selected on the basis of crossand auto-correlation method as proposed by Sudheer et al. [2]. The significant input variables were found to be the effective rainfalls at lag time steps of t − 9, t − 8, and t − 7 (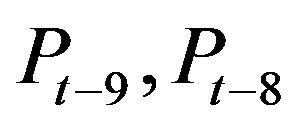 an d
an d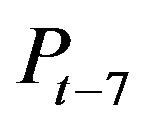 ) using the crosscorrelation and the river flow values at lag time steps of t − 1 and t − 2 (
) using the crosscorrelation and the river flow values at lag time steps of t − 1 and t − 2 (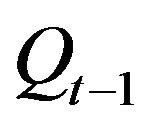 and
and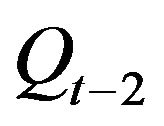 ) using the autocorrelation function [23]. The output of the model is the riverflow at time t (
) using the autocorrelation function [23]. The output of the model is the riverflow at time t (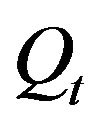 ). Thus Qt is represented as
). Thus Qt is represented as
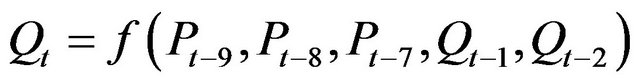 (4)
(4)
In this study, the hourly input data are divided into two cases based on the previous data sets1) Rise: In the rise pattern the value of runoff at time t is greater than that of time step t − 1, i.e.,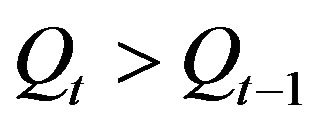 .
.
2) Fall: In the fall pattern the value of runoff at time t − 1 is greater than that of time step t, i.e.,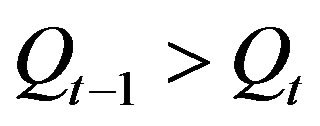 .
.
Figure 2 shows the proposed methodology in which Model 1 decomposes the data into classes (i.e., rise and fall) based on the input variables, Model 2 is the calibrated ANN, model for the rise and Model 3 is the calibrated ANN model for the fall.
Statistical indices like the coefficient of correlation (Cc), root-mean-square error (RMSE) and Nash-Sutcliffe efficiency (NSE) [24] are used to evaluate the performance of the model. The equations of these statistical indices are,
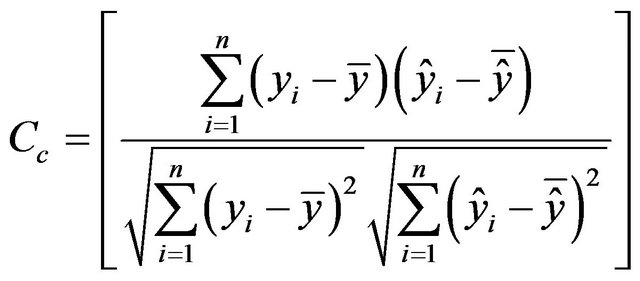 (5)
(5)
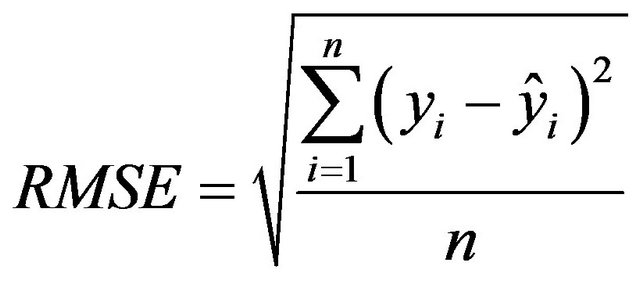 (6)
(6)
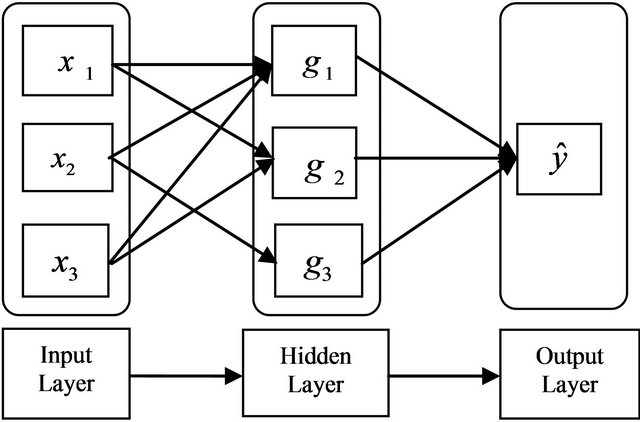
Figure 1. Typical model structure of the FF-ANN model.
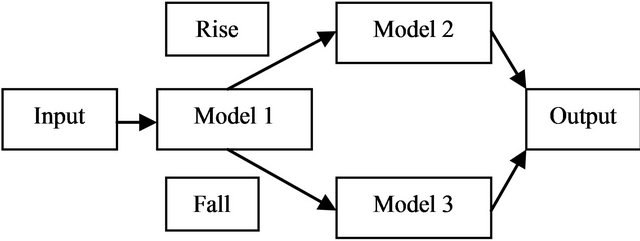
Figure 2. Methodology of the streamflow decomposed based ANN model.
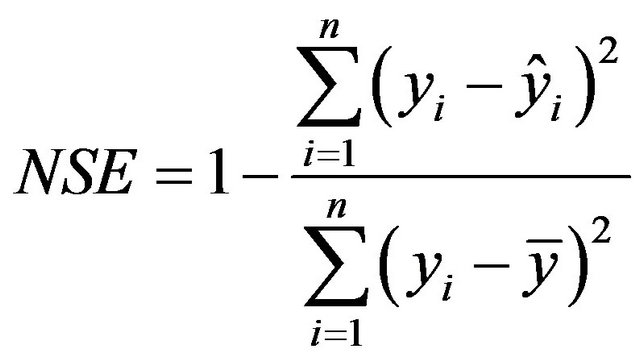 (7)
(7)
where,
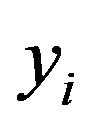 is the Observed Runoff Value,
is the Observed Runoff Value, 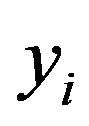 is the Predicted Runoff Value, y is the mean of the observed runoff values and
is the Predicted Runoff Value, y is the mean of the observed runoff values and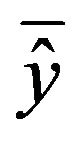 is the mean of the predicted runoff values.
is the mean of the predicted runoff values.
4. Case Study
A case study on the Kolar River basin is chosen to demonstrate the proposed SD-ANN method. FF-ANN and SD-ANN models for forecasting the runoff values at 1-hour lead time have been developed. Data relating to monsoon season (i.e., July, August, and September) for 3 years period (from 1987 to 1989). Note that areal average values of rainfall data for three rain gauge stations were used in the study.
The Kolar River is a tributary of the river Narmada that drains an area about 1350 km2 before its confluence with Narmada near Neelkant (Figure 3). In this study the catchment area up to the Satrana gauging site is considered, which constitutes an area of 903.87 km2. The 75.3-km-long river course lies between north latitude 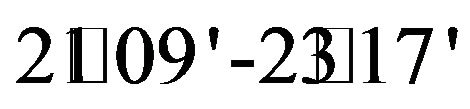 and east longitude
and east longitude 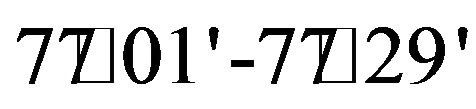 Further more details on the basin are given by Nayak et al. [25].
Further more details on the basin are given by Nayak et al. [25].
From the total available data for 3 years, 6525 patterns (input-output pairs) were identified for the study and were split into calibration (5500 sets, 1987-1988 data sets) and validation (1025 sets, 1989 data sets). Note that the 1025 sets considered for validation were corresponding to a continuous hydrograph.
The activation function used at the hidden layer and at the output layer is sigmoid function as it is easily differentiable.
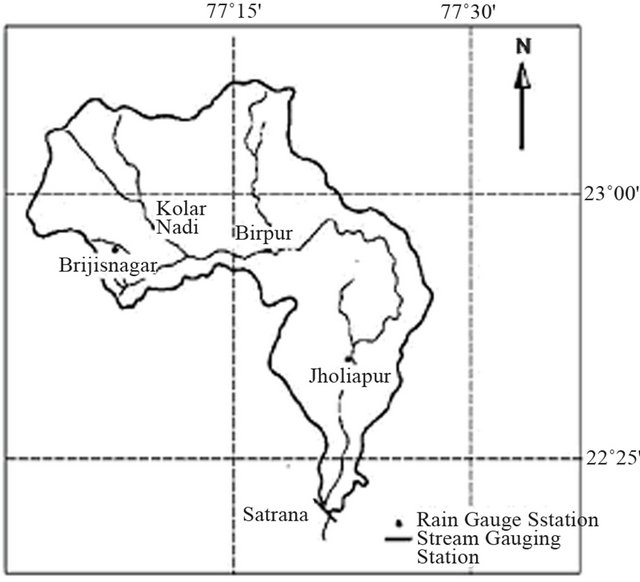
Figure 3. Map of Kolar river basin [25].
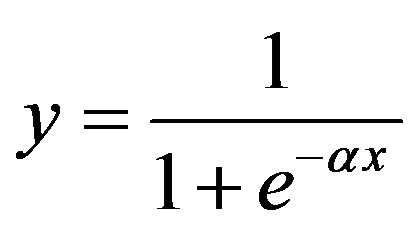 (8)
(8)
To calculate the network parameters back propagation algorithm [26] has been used. Adaptive learning and momentum rates have been employed for the model training [25].
5. Results and Discussions
As discussed earlier, the SD-ANN model developed is used for forecasting the river flow for Kolar Basin at a lead time of 1 hour. The performance of the proposed SD-ANN model and FF-ANN model have been evaluated by means of a variety of statistical criteria such as coefficient of correlation (CC), coefficient of efficiency (NSE) and the root-mean-square error (RMSE) between the actual and estimated flow values. The various statistics stated below in Table 1 indicates that the predicted value of runoff by the SD-ANN is more accurate than that of FF-ANN Model. Performance of both the models in terms of statistical indices is very similar and satisfactory as the correlation coefficient of both the models are very close to the unity. Further it is observed from the Table 1 that the efficiency of both the models is greater than 90% which is highly satisfactory according to Shamseldin [27]. In addition, it is worth noting that the RMSE of the proposed model is less when compared to the FF-ANN model. Also the prediction of high flows is well modeled by the proposed SD-ANN model when compared to the FF-ANN model (Figure 4). It is evident from the results that the decomposition of the streamflow has considerable impact on the performance of models.
Table 1. Statistical indices—comparison between SD-ANN and FF-ANN model.
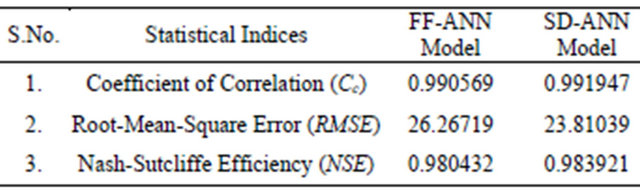
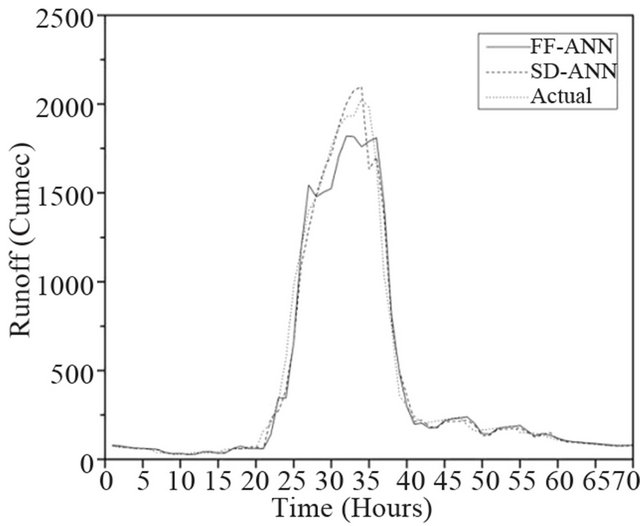
Figure 4. Computed streamflows for a typical event during validation.
6. Summary and Conclusion
In this study, a simplified ANN based decomposed streamflow model is developed. The proposed data decomposition does not require any prior knowledge or understanding of physical processes. In this study the data is divided into two states namely rise and fall, based on the current state. The performance of the proposed SD-ANN model is compared to that of the feed-forward ANN model in terms of statistical indices such as coefficient of correlation, coefficient of efficiency and root means square error. The exercise was carried out for the hourly data in Kolar river basin, India. It is observed that the proposed SD-ANN model and the FF-ANN model show similar results in terms of statistical indices except the case of RMSE where the former outperforms the latter. Further, the SD-ANN model outperforms the FFANN model in prediction of high flows. The results show the significance of the streamflow decomposition when compared to single hydrograph. The performance of the SD-ANN models has to be tested on various time scales. Further extensions of this model can be examined to improve the forecasting accuracy [28].
7. Acknowledgements
The authors thank the Vellore Institute of Technology, Vellore, India, for providing the necessary facilities to carry out this research work.
REFERENCES
- C. E. Imrie, S. Durucan and A. Korre, “River Flow Prediction Using Artificial Neural Networks: Generalization beyond the Calibration Range,” Journal of Hydrology, Vol. 233, No. 1-4, 2000, pp. 138-153. doi:10.1016/S0022-1694(00)00228-6
- K. P. Sudheer, A. K. Gosain and K. S. Ramasastri, “A Data-Driven Algorithm for Constructing Artificial Neural Network Rainfall-Runoff Models,” Hydrological Processes, Vol. 16, No. 6, 2002, pp. 1325-1330. doi:10.1002/hyp.554
- A. Jain and S. Srinivasulu, “Integrated Approach to Model Decomposed Flow Hydrograph Using Artificial Neural Network and Conceptual Techniques,” Journal of Hydrology, Vol. 317, No. 3-4, 2005, pp. 291-306.
- J. G. Arnold, P. M. Allen, R. Muttiah and G. Bernhardt, “Automated Base Flow Separation and Recession Analysis Techniques,” Ground Water, Vol. 33, No. 6, 1995, pp. 1010-1018. doi:10.1111/j.1745-6584.1995.tb00046.x
- M. E. Spongberg, “Spectral Analysis of Base Flow Separation with Digital Filters,” Water Resources Research, Vol. 36, No. 3, 2000, pp. 745-752. doi:10.1029/1999WR900303
- L. C. Smith, D. L. Turcotte and B. L. Isacks, “Streamflow Characterization and Feature Detection Using a Discrete Wavelet Transform,” Hydrological Processes, Vol. 12, No. 2, 1998, pp. 233-249. doi:10.1002/(SICI)1099-1085(199802)12:2<233::AID-HYP573>3.0.CO;2-3
- D. Labat, R. Ababou and A. Mangin, “Rainfall-Runoff Relations for Karstic Springs. Part II: Continuous Wavelet and Discrete Orthogonal Multiresolution,” Journal of Hydrology, Vol. 238, No. 3-4, 2000, pp. 149-178. doi:10.1016/S0022-1694(00)00322-X
- S. Y. Liu, X. Z. Quan and Y. C. Zhang, “Application of Wavelet Transform in Runoff Sequence Analysis,” Progress in Nature Science, Vol. 13, No. 7, 2003, pp. 546- 549.
- F. Anctil and D. G. Tape, “An Exploration of Artificial Neural Network Rainfall-Runoff Forecasting Combined with Wavelet Decomposition,” Journal of Environmental Engineering and Science, Vol. 3, No. 1, 2004, pp. S121- S128. doi:10.1139/s03-071
- B. Zhang and S. Govindaraju, “Prediction of Watershed Runoff Using Bayesian Concepts and Modular Neural Networks,” Water Resources Research, Vol. 36, No. 3, 2000, pp. 753-762. doi:10.1029/1999WR900264
- D. Furundzic, “Application Example of Neural Networks for Time Series Analysis: Rainfall Runoff Modeling,” Signal Processing, Vol. 64, No. 3, 1998, pp. 383-396. doi:10.1016/S0165-1684(97)00203-X
- R. J. Abrahart and L. See, “Comparing Neural Network and Autoregressive Moving Average Techniques for the Provision of Continuous River Flow Forecasts in Two Contrasting Catchments,” Hydrological Processes, Vol. 14, No. 11-12, 2000, pp. 2157-2172. doi:10.1002/1099-1085(20000815/30)14:11/12<2157::AID-HYP57>3.0.CO;2-S
- K. L. Hsu, H. V. Gupta, X. Gao, S. Sorooshian and B. Imam, “Self-Organizing Linear Output Map (SOLO): An Artificial Neural Network Suitable for Hydrologic Modeling and Analysis,” Water Resources Research, Vol. 38, No. 12, 2002, pp. 1-17. doi:10.1029/2001WR000795
- K. Hsu, V. H. Gupta and S. Sorooshian, “Artificial Neural Network Modeling of the Rainfall-Runoff Process,” Water Resources Research, Vol. 31, No. 10, 1995, pp. 2517- 2530. doi:10.1029/95WR01955
- N. Sajikumar and B. S. Thandaveswara, “A Nonlinear Rainfall-Runoff Model Using an Artificial Neural Network,” Journal of Hydrology, Vol. 216, No. 1-2, 1999, pp. 32-55.
- K. P. Sudheer, P. C. Nayak and K. S. Ramasastri, “Improving Peak Flow Estimates in Artificial Neural Network River Flow Models,” Hydrological Processes, Vol. 17, No. 3, 2003, pp. 677-686. doi:10.1002/hyp.5103
- M. J. Zurada, “An Introduction to Artificial Neural Systems,” West Publishing Company, St Paul, 1997.
- G. J. Bowden, G. C. Dandy and H. R. Maier, “Input Determination for Neural Network Models in Water Resources Applications: 1. Background and Methodology,” Journal of Hydrology, Vol. 301, No. 1-4, 2004, pp. 75-92.
- G. J. Bowden, G. C. Dandy and H. R. Maier, “Input Determination for Neural Network Models in Water Resources Applications: 2. Background and Methodology,” Journal of Hydrology, Vol. 301, No. 1-4, 2004, pp. 93- 107.
- K. C. Luk, J. E. Ball and A. Sharma, “A Study of Optimal Model Lag and Spatial Inputs to Artificial Neural Network for Rainfall Forecasting,” Journal of Hydrology, Vol. 227, No. 1-4, 2000, pp. 56-65. doi:10.1016/S0022-1694(99)00165-1
- D. Silverman and J. A. Dracup, “Artificial Neural Networks and Long-Range Precipitation Prediction in California,” Journal of Climate and Applied Meteorology, Vol. 39, No. 1, 2000, pp. 57-66. doi:10.1175/1520-0450(2000)039<0057:ANNALR>2.0.CO;2
- H. R. Maier and G. C. Dandy, “Neural Networks for the Prediction and Forecasting of Water Resources Variables: A Review of Modeling Issues and Applications,” Environmental Modelling & Software, Vol. 15, No. 1, 2000, pp. 101-124. doi:10.1016/S1364-8152(99)00007-9
- R. K. Srivastav, K. P. Sudheer and I. Chaubey, “A Simplified Approach to Quantifying Predictive and Parametric Uncertainty in Artificial Neural Network Hydrologic Models,” Water Resources Research, Vol. 43, No. 10, 2007, Article ID: W10407. doi:10.1029/2006WR005352
- J. E. Nash and J. V. Sutcliffe, “River Flow Forecasting through Conceptual Models: 1. A Discussion of Principles,” Journal of Hydrology, Vol. 10, No. 3, 1970, pp. 282-290. doi:10.1016/0022-1694(70)90255-6
- P. C. Nayak, K. P. Sudheer, D. M. Rangan and K. S. Ramasastri, “Short-Term Flood Forecasting with a Neurofuzzy Model,” Water Resources Research, Vol. 41, No. 4, 2005, Article ID: W04004. doi:10.1029/2004WR003562
- D. E. Rumelhart, G. E. Hinton and R. J. Williams, “Learning Representations by Back-Propagating Errors,” Nature, Vol. 323, No. 6088, 1986, pp. 533-536. doi:10.1038/323533a0
- A. Y. Shamseldin, “Application of a Neural Network Technique to Rainfall-Runoff Modelling,” Journal of Hydrology, Vol. 199, No. 3-4, 1997, pp. 272-294. doi:10.1016/S0022-1694(96)03330-6
- P. Mittal, S. Chowdhury, S. Roy, N. Bhatia and R. Srivastav, “Dual Artificial Neural Network for Rainfall-Runoff Forecasting,” Journal of Water Resource and Protection, Vol. 4, No. 12, 2012, pp. 1024-1028. doi:10.4236/jwarp.2012.412118

