Received 13 October 2015; accepted 8 January 2016; published 11 January 2016

ABSTRACT

The expansion of non-industrial private forests (NIPF) in Ireland is unique in the European context in which the almost doubling of forest cover within the last thirty years has taken place largely on farmland. This is not surprising as Ireland has some of the highest growth rates for conifers in Europe and also has a large proportion of land which is marginal for agriculture but highly productive under forests. However, in recent years, afforestation in Ireland as in many European countries has fallen well short of policy targets. As the farm afforestation decision essentially involves an inter-temporal land use change, farmers need comprehensive information on forest market returns under different environmental conditions and forest management regimes. This paper describes the systematic development of a cohort forest bio-economic model which examines financially optimal afforestation and management choices. Simulating a range of productivity and harvesting scenarios for Sitka spruce, we find that different objectives result in different outcomes. We see substantial differences between the biologically optimal rotation, the reduced rotation in common usage and the financially optimal rotation which maximises net present value and find that the results are particularly sensitive to the choice of management and methodological assumptions. Specifically, we find that better site productivity and thin versus no-thin options result in shorter rotations across all optimisations, reinforcing the usefulness of this type of financial modelling approach. This information is critical for future policy design to further incentivise afforestation of agricultural land.

Keywords:

Forestry, Bio-Economic Modelling, Afforestation, Optimisation

1. Introduction

In recent years, afforestation in Ireland as in many European countries has fallen well short of policy targets (Eurostat, 2013) . This comes at a time when the importance of the ecosystem services provided by forests is increasingly valued (EC 2013). The explicit role of afforestation in moving towards carbon neutrality and greenhouse gas mitigation was recognised by the EU Council of Ministers in 2014 (EUCO, 2014) and policy makers are now looking at ways to mitigate greenhouse gas production as agricultural production is increased in response to increasing global demands for food. In Ireland, the agri-food sector is responding by significantly expanding dairy and beef production (DAFM, 2015) .

The expansion of non-industrial private forests (NIPF) in Ireland is unique in the European context in which the almost doubling of forest cover within the last thirty years has taken place largely on farmland. On the one hand this is not surprising as Ireland has some of the highest growth rates for conifers in Europe and also has a large proportion of land which is marginal for agriculture but highly productive under forests (Farrelly et al., 2011) . In addition, the expansion was facilitated by a series of Irish and EU subsidies which incentivised the afforestation of agricultural land. On the other hand, the rate of expansion is surprising given the disincentive presented by the permanency of the land use change decision. Irish legislation imposes replanting conditions on all felled forests, so the decision to plant is not taken lightly by farmers. The rapid increase in forest cover is also surprising given the low level of knowledge of the economics of forestry, or tradition of forest management among farmers. In addition, farmers are unfamiliar with the long crop rotation and consequential uncertainty around future forest returns.

These factors create difficulty for policy makers in further incentivising afforestation of agricultural land. The afforestation of farmland is essentially an inter-temporal land use change decision which is confounded by changing and uncertain prices over the forest life-cycle. Most forest research focuses either on the silvicultural aspects of forest management, or the optimisation of an objective function to answer specific policy questions. Few, if any deal with decision-making at farm level. The choices that farmers make with respect to site type, species selection, management and harvesting decisions depend on their objectives and will result in different growth, cost and income curves and ultimately different rotations.

The objective of this research is to develop a forest bio-economic model with the capacity to model different afforestation and forest management choices with consequentially different optimal financial rotations to inform an increasingly important sector in which prices and policies are changing over time. First we review the biophysical theory underpinning forest growth, so that we can understand how output can be manipulated. Next we review the scientific literature on forest bio-economic models in order to inform the assumptions necessary to model the relevant choices. We justify the assumptions and data needed to develop such a model and illustrate these with descriptive statistics. We generate growth, cost and income curves by species, yield and management scenarios for different optimisations. We conduct sensitivity analysis on the results and comment in relation to afforestation targets and evolving forest policy.

2. Theoretical Framework

Farmers considering afforestation need to know the economic implications of different forest establishment, management and harvesting regimes. This information enables decisions on 1) whether to plant or not and 2) how to optimise the returns from the forest depending on owner objectives and 3) what are the outcomes of different optimisations? Farmers need to understand the implications of the choices they make:

1) Do they tie up land in forestry or continue with agriculture?

2) How does varying the species, the productivity of the planting site, the harvesting regime or the rotation length impact on the optimum return?

3) What impact do varying costs, subsidies, timber prices and interest rates have on the return?

4) What is the optimal rotation length for different species and different objectives?

The quantification of the agronomic and economic life-cycle components of the return to forestry under different circumstances is necessary to estimate the different outcomes arising from different optimisation objectives. This information is also necessary for the successful implementation of policies with different objectives ranging from the optimisation of raw material production for timber processing and wood biomass and the carbon sequestration potential of forests (European Commission, 2013) .

2.1. Tree Growth

Knowing how forest trees grow is vital to understanding what species to plant, when to thin or carry out a final harvest (clearfell) and how to manipulate timber yields. This section addresses the scientific theory underpinning the biological and economic interactions which determine forest market returns under different management and financial objectives. The detailed understanding and specification of the relevant assumptions and interactions is sometimes the greatest challenge faced by inter-disciplinary researchers (Flichman & Allen, 2013; Janssen et al., 2010) . In general, afforestation (planting of previously un-forested land) results in even-aged stands of species with similar growth habits which facilitates prediction of growth rates (in comparison with the wide variety of species and age-classes often found in natural forests). Growth patterns differ between different environmental site conditions and between conifers and broadleaf trees. Annual weather conditions affect the amount of growth (increment) in any given year but overall, individual species in Britain and Ireland display similar average growth patterns.

Typically, trees grow vigorously in the very early years and then begin to stabilise growth rates in the middle years before slowing down as they get older. The mean annual increment (MAI) or mean annual growth refers to the average growth per year a tree or stand of trees has exhibited/experienced to a specified age. From a scientific perspective, the typical growth pattern of most trees approximates to a sigmoid curve (Smith, 1986) . The MAI starts out small, increases to a maximum value as the tree matures, then declines slowly over the remainder of the lifetime of the stand of trees. Throughout this, the MAI always remains positive and is calculated as per Equation (1) (Husch et al., 1982) .

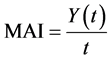(1)

where Y(t) = yield at time t.

MAI differs from periodic annual increment (PAI) which is the growth for one specific year (current annual increment (CAI)) or any other specified period of time (Bettinger et al., 2010) . In economic terms, this is the marginal change in growth in an individual year (Husch et al., 1982) . The point where the MAI and PAI meet is typically referred to as the biological rotation age. This is the age at which the tree or stand would be harvested if the management objective is to maximize long-term yield and is determined by differentiating MAI (t) with respect to that represented in Figure 1.

The intersection of the MAI and PAI curves is the point of maximum MAI (mMAI). This point defines the potential productivity of a stand of trees i.e. the yield class of a stand of trees. The yield class then determines the maximum volume production of a given species on a given site. For example, a hectare (ha) of trees with a maximum MAI of 20 cubic metres (m³) per year has a yield class of 20 and has an average timber yield of 20 m³/year. Typically, yield classes for different species are determined by factors such as soil type, elevation, drainage and vegetation. This general pattern of growth is typical of all even-aged stands of trees but the rate of growth differs greatly by species and can vary within species under different environmental conditions.

2.2. Forest Management and Harvesting Decisions

After a number of years of what is termed “free growth”, trees begin to compete with each other and the removal of a proportion of the trees (thinning) is usually considered at this stage. Thinning increases the growing space for the remaining trees and once adapted to the new situation, they respond by accelerating diameter growth and crown development.

The primary objective of thinning is to end up with a smaller number of trees of larger diameter which have higher value end uses thus increasing economic return. Thinning immediately results in a decrease in stand level growth rate but this is eventually outweighed by the accelerated diameter growth of the remaining trees (Kerr & Haufe, 2011) . From an economic perspective, thinning provides periodic returns to the farm forest owner as the crop matures and improves the biodiversity of the forest. However, thinning may not always be possible if for example, road access for timber removal is not sufficient or if site conditions such as high elevation or poor drainage increase the risk of trees being up-rooted (wind-throw).

2.3. Optimal Forest Rotations

The general patterns of tree growth discussed here are typical of all even-aged stands of trees. Thus generalised forecasts of tree growth can be modelled for different species in different environmental conditions on the basis of actual growth data. The primary data needed to forecast growth are species, age and yield class. Growth forecasts can be used to predict volume production at a given age and are also used to determine the optimum rotation for forests depending on management objectives.

In population ecology and economics, maximum sustainable yield (MSY) can be defined as the largest yield that can be harvested which does not deplete the resource (timber) irreparably and which leaves the resource in good shape for future use. Biologists use this concept of maximum sustainable yield (MSY) which equates to mean annual increment (MAI), to determine the optimal harvest age of timber. The point at which the MAI peaks is commonly used to identify the biological maturity of the tree, and its readiness for harvesting. This point is also equivalent to the intersection of the MAI and the periodic annual increment (PAI) curves as in Figure 1.

Thus the biological optimum rotation is the age at which the tree or stand is harvested if the management objective is to maximize long-term yield. However, forests may also be managed with the objective of returning the greatest revenue. Since benefits are generated over multiple years, it is necessary to calculate that particular age of harvesting which will generate the maximum revenue. The financially optimum forest rotation occurs at the age at which the net present value (NPV) of the crop is maximised. This is calculated by discounting for future expected benefits by subtracting the present value of costs from the present value of revenue (Husch et al., 1982) . The financially optimum rotation age is determined at point R in Figure 2 which shows the maximum net

present value of expected benefit/profit. Harvesting at any age before or after R will result in a lower expected benefit/profit. In economic terms, this is the point at which the marginal benefits equal the marginal costs (Varian, 2010) . Growing the crop beyond this point would result in a net revenue loss.

While growth curves tend to be sigmoidal in shape, cost and income curves tend to be uneven as the majority of costs arise early in the rotation and incomes arise later. The challenge here is to develop a methodology to generate information based on the fundamental principles of tree growth with the flexibility to manipulate forest output and to address costs and price changes over time, to reflect a wide range of optimisation choices.

3. Methodology and Data

This section focuses on the methodological development of a forest bio-economic model. Initially we examine the objectives and choices employed in answering a range of policy and optimisation questions in other published models. Learning from these we decide on the choices that should be incorporated into our model and adapt and build on existing methodologies to suit Irish conditions where possible.

An international literature review of models that specifically address forestry issues shows that the policy questions covered vary widely in relation to objectives and methodologies. Table 1 presents a summary of some of the model types, objectives and variables analysed.

Regardless of their objectives, the reviewed models deal with different management scenarios and the consequences that these have on rotation length and revenue over the life-cycle of the forest. The models differ most widely in their optimisation objectives:

1) For some, the objective is to optimise rotation length by manipulating thinning intensity and timing of harvesting, thereby accruing timber revenues earlier.

2) For others, the objective is to optimise the utilisation of the timber produced by manipulating the diameter and taper on logs to produce the most valuable logs.

3) On the other hand, carbon optimisation may involve lengthening the rotation to avoid carbon losses.

4) Most of the papers reviewed model harvesting decisions. Few model the full forest cycle to take account of the consequences of afforestation as well as management decisions on forest returns.

In countries such as Australia and New Zealand where a large proportion of forest cover is in farm ownership, a number of the bio-economic models are whole-farm afforestation models. The whole-farm bio-economic model which is most relevant for the Irish context is the Australian Farm Forestry Financial Model, (AFFFM) developed by Herbohn et al. (2009) which is primarily an extension tool. It provides information on the financial effect of adding forestry to the existing farm enterprise (s), taking the opportunity cost into account. Timber yields are calculated for various soil types using mean annual increment (MAI) estimates and yield tables. Financial outputs include net present value, land expectation value and internal rate of return. The AFFFM is particularly useful as it contains a detailed description of the model inputs which allows us to further develop and adapt many of the AFFFM choices and options.

3.1. Methodological Choices

Having reviewed existing models, we provide a general summary of the methodological choices and options examined in these models in Table 2.

On the basis of the choices examined in the published models, we select the relevant methodological options for each of the choices we intend to model. In describing these elements in detail and discussing how they may be adapted to the Irish afforestation context, we essentially describe the development of the assumptions under-pinning our model which we call ForBES (Forest Bio-Economic System) model.

3.2. Valuation Methodology

In order to capture the life-cycle implications of different afforestation and forest management choices, it is necessary to utilise a life-cycle framework. Discounted cash flow (DCF) is the most widely used methodology for determining the economic value of a forest or a parcel of bare land still to be afforested (Hiley, 1954; Bettinger et al., 2010) . In the models reviewed, the choice of calculation methodology depends on whether the period of analysis reflects one rotation or an infinite number of rotations. Our primary interest is to be able to ultimately compare annual returns from an agricultural enterprise with a forest rotation. Thus we will calculate the returns

for one rotation (and include the capacity to extend the rotation to estimate carbon storage over the full growth cycle of trees). DCF generates the net present values (NPV) of future costs and incomes and discounts these costs and incomes to the present day at a target rate of interest (Hiley, 1954 & 1956) . The NPV of the whole income stream is the sum of the present values of the annual amounts in the income stream as presented in Equation (2) (assuming a constant discount rate).

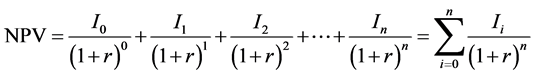(2)

where I is the annual income (or cost), r is the discount rate and n is the number of years.

A number of points arise in examining the calculation of the NPV (holding all other factors constant):

Firstly, when income amounts are high, the NPV will be high and vice versa.

It also holds that the NPV will be higher if profits arise earlier during the rotation.

The life span of the investment (rotation) also has a large effect on the economic return as longer forest rotations will have lower NPV’s than shorter rotations.

In the case of a forest, income and costs can accrue unevenly over the rotation (generally costs arise in the early years and incomes accrue in later years).

This highlights a limitation of the methodology in that it is only possible to directly compare the NPV’s of two investments (in our case land uses) if both investments have the same life span (Boardman et al., 2011) . This is particularly important in our case as our model also needs to have the capacity to be used as a forest extension tool in the context of land use change decision support. Thus we need to annualise the NPV so that it can be expressed on the same basis as annual agricultural returns. The AFFFM which is used in an extension capacity also calculates forest returns in terms of annual equivalised (AE) values of the NPV (Herbohn et al., 2009) . The AE value is calculated using Equation 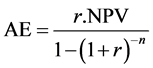(3).

(3)

The discount rate chosen for NPV calculation can significantly increase or decrease the NPV of an afforestation project. For a forest investment with the common pattern of incurring costs in the early years and not accruing profits until later, a higher discount rate will reduce the NPV. In relation to policy recommendations, a high discount rate favours or strengthens the case for projects where benefits are front-loaded, whereas a low discount rate favours projects with back-end loaded benefits (Boardman et al., 2011) . The convention is to ignore any effects of possible inflation, as this cannot be predicted, therefore the return is regarded as a “real” rate of return. Phillips et al. (2013) note that there are many opposing views about the “correct” discount rate to use, internationally as well as nationally. Thus the capacity to conduct sensitivity analysis of the discount rate adds greatly to any forest valuation exercise.

3.3. Site Selection and Species Choice

In Ireland, broadleaf species have longer rotations than conifers and more fertile soils are more productive for both broadleaf and conifer species. However, broadleaf species are more site-demanding than conifers and require reasonably fertile soil types. Broadleaves are also less tolerant of exposure to wind and require sheltered, well-drained soils. The decision to plant broadleaf species is generally made on the basis of environmental or aesthetic concerns as the slow growth rates (compared to conifers) lead to long rotations and low economic return. On the other hand, many conifer species require less demanding site conditions. Sitka spruce (SS) (Piceasitchensis (Bong.) Carr.) is a highly productive tree species on wet mineral soils which are marginal or sub- marginal for agriculture (Farrelly et al., 2011) . We report our analysis in relation to the most commonly planted species (Sitka spruce), which accounts for 57 percent of all planting in Ireland (Forest Service 2013) which is carried out on the basis of a one hectare unit, which allows for later per hectare comparisons between forestry and agricultural returns.

Another factor which affects species choice is the availability of differential afforestation grants and annual subsidies for broadleaf and conifer species for up to 15 or 20 years. In general, the annual subsidies for broadleaves are considerably higher than conifers. Farmers’ objectives may involve trade-off between higher short- term subsidy income from broadleaves or earlier timber income from conifers, in relation to species selection. While the main objective of this chapter is to develop a mechanism to estimate forest market returns, we also calculate NPV’s with and without subsidies to assess their impact on overall forest returns. Our analysis is carried out on the basis of a one hectare unit, which will facilitate later per hectare comparisons between forestry and agricultural returns.

3.4. Forest Yield Models

Forest yield models provide predictions of potential timber volumes depending on species, site productivity and management regimes. The yield models utilised in the reviewed BEM’s have been developed to reflect country/region specific growth rates and timber production under given environmental conditions. Yield models may be either static (assume a given starting position and management regime) or dynamic (actual growth data are inputted and management regimes can be manipulated). Many of the reviewed BEM’s are interested in manipulating stand growth where actual growth data exist (Halbritter & Deegen, 2015; Tahvonen et al., 2013; Diaz-Bal- teiro & Romero, 2003; West et al., 2012; Pihlainen et al., 2015; Vanclay, 1998) and are thus able to use mathematical dynamic models which allow for optimisation of timber production growth by varying management choices such as intensity and timing of thinning and timing of ultimate harvest.

Conversely, afforestation BEM’s need to utilise static models as growth data do not exist either because the stand is not sufficiently old to collect the required data, or because the model is required to produce a growth prediction for an as yet unplanted forest. The disadvantage of static models is that they assume that stands are managed to a prescribed pattern over the rotation and do not allow for manipulation of management regimes.

Within a European context the UK Forestry Commission (FC) yield models developed by Edwards and Christie (1981) are the best-known example of static yield models (Broad & Lynch, 2006) . The models calculate age of MAI for a range of species and yield classes and forecast mean tree volumes based on actual stand growth data from British forests (Edwards & Christie, 1981) . The FC yield models which are widely used in Ireland, have provided a uniform platform from which to forecast timber volumes (Phillips et al., 2011) based on MAI. As this analysis involves the prediction of timber volumes in the absence of growth data, we choose to build on the FC models to calculate rotations based on mMAI in developing our Teagasc Forest Bio-Economic System model (ForBES).

3.5. Thin or No-Thin?

Once trees begin to compete with each other for light and nutrients, a decision is needed as to whether to thin the forest or allow it to grow to maturity without thinning. Thinning can be costly, (particularly the first thinning) as the cost of harvesting a large number of small, low value trees is high. In Ireland, as many forests are planted on exposed or poorly drained marginal land these forests may be at risk from wind-blow and the appropriateness of thinning needs to be considered carefully. An un-thinned forest has a high number of small diameter trees, whereas a thinned forest of similar yield class has a smaller number of larger diameter trees. The dbh¹ (diameter at breast height) of a tree determines the end-use of the logs produced, which in turn determines the value. In general, larger dbh trees are more valuable as they have a wider range of high value end-uses. Ultimately, the difference in return between thinned and unthinned forests may depend on the log categories and the relative category prices prevailing at time of harvest. We will examine the financial impact of thinning on forest returns across a range of yield classes.

3.6. Manipulation of Volume Output

Methods to optimize timber returns in the reviewed BEM’s focus on varying the thinning intensity, thinning type and thinning interval to manipulate the resulting volume and log categories. The maximum sustainable intensity of thinning employed in Britain and Ireland is marginal thinning intensity (MTI) which is defined in gross volume terms as 70 percent of yield class per hectare per year (m³/ha/year)². Static yield models dictate the timing of thinning and clearfell as a function of age and top height³ of a stand of trees.

Due to fast growth rates in Ireland for some conifer species, the current industry norm is to grow crops to a “reduced rotation” of (mMAI) (the reduced rotation for Sitka spruce involves harvesting at the age of mMAI less 20 percent). This practice is based on an economic analysis (Anon, 1977) and is more or less in line with the theoretical financially optimum rotation for the major tree species (Phillips, 1998 & 2004) . The capacity to calculate these reduced rotations will be included in ForBES.

3.7. Calculation of Timber Revenues

In Ireland, there are essentially two methods of selling timber which ultimately dictate the pricing structure used. Timber is commonly sold either “standing” (un-harvested) or “harvested” and pre-cut into specific lengths depending on the required end-products (timber assortments). In all models reviewed, the methodology applied to the calculation of timber revenues is critical to predicting the market return to forests. In general, dynamic models have greater flexibility than static models in relation to assortment and price optimisation.

Standing sales are sold on the basis of the volume of the average (mean) tree predicted by static yield models, whereas the prediction of revenues for harvested timber sales requires information on prices for different size assortments and the breakdown of potential end-products for the stand. However, historic assortment price data is not as readily available as mean tree price series data. Therefore many analyses use historic price-size curve data, particularly when estimating timber revenues far into the future.

3.7.1. Income Streams

All market and non-market incomes should be included in the calculation of income streams. Forest establishment, management and harvesting costs are subtracted from revenues to give future net cash flows. We would also like to include the agricultural opportunity costs into NPV calculations at a future date. Without opportunity costs, we can compare different forest management options. With opportunity costs, we can compare planting decisions.

The global nature of the timber trade leads to uncertainty around future timber prices which have a large impact on predicting forest income streams. The higher the price applied, the higher the long term return, whereas using current prices can result in significant variation in value year on year. To overcome this, many practitioners use historic average price series (Phillips, 2013) . The number of years to clearfell will influence the choice of the price series. The use of shorter time series is only appropriate if a forest is close to clearfell. Longer term price series should be used otherwise.

Since the 1990’s, Coillte (State Forestry Board) has recorded conifer standing prices in a range of size categories on a regular basis. Data are published annually by the Irish Timber Growers Association (ITGA, 2014) in mean tree size categories. This is by far the most comprehensive and representative source of timber prices. As there are currently no published price series data for timber assortments in Ireland, we generate a ten year historic price series using price size curves for mean tree volumes as presented in Figure 3. Mean tree volume is plotted against the relevant timber prices for mean tree size categories, generating a price-size curve as illustrated in Figure 3. The mean tree value (€/m³) is then multiplied by the number of stems (sph) to arrive at a per

hectare timber revenue. All prices are deflated to the relevant year using the Consumer Price Index (CPI) (CSO, 2014) before being averaged. We assume that timber prices keep pace with inflation as they have over the period that price data have been recorded (Ryan et al., 2013) .

An assumption underlying many of the reviewed BEM’s is that the costs and returns to the forest enterprise remain static and that all prices (e.g. establishment and continuing maintenance costs, timber and other revenues) change over time due to inflation. This means that a “real” discount rate is used when discounting cash flows. In using the average consumer price index to inflate values over time we assume that goods change value at the same rate. However, this is not always the case. A farmer considering forestry is likely to make a decision on the basis of both agricultural and forestry costs and prices prevailing at that time rather than over a long time horizon. Thus we will examine the impact of using average Consumer Price Indices and good/service specific indices (CSO, 2014) in the calculation of NPV’s. Here we compile good specific price and cost indices for 11 components of cost and income from 1985 to 2014 to which we apply the individual annual inflation rates (See Appendix 1 for detail).

3.7.2. Cost Streams

The agronomic costs of establishing, managing and harvesting a forest vary according to species, site conditions and management objectives. Generalised costs are usually readily available as many of the operations have standard procedures and operating costs. In general terms, most costs are incurred within the first four years and generally consist of ground cultivation and drainage, fencing, planting, fertilising (on less productive sites only), replacement of dead trees and vegetation management. However, the burden of these costs may have to be carried for the life-time of the rotation, unless they can be offset by subsidies. The treatment of reforestation costs varies in the reviewed BEM’s. Theoretically, the reforestation cost should be attributed to the next rotation, however if only one rotation is being valued, debate exists over whether the cost of reforestation should be included as a cost at the end of the current rotation or the start of the next rotation (Clinch, 1999; Bateman et al., 2006) . The argument here is that forest owners cannot legally harvest without replanting. From this perspective, the capacity to assess the sensitivity of the NPV to the inclusion or exclusion of reforestation cost is also necessary in the ForBES.

The collection of forest inventory data in preparation for timber sales and harvesting is time-consuming and costly and is applied indirectly as a percentage timber volume reduction. The cost of sales for both conifer and broadleaf forests is higher in percentage terms for thinnings (12 percent) than for clearfells (5 percent). The cost of sales for poorer quality, lower value timber will be high compared to the percentage cost incurred for high value stands. The model also includes the option to include or exclude harvest losses arising as a result of timber being damaged or left on site. On the basis of analysis carried out by Phillips et al. (2009) , these losses can be significant. All conifer merchantable timber volumes (MTV) generated by ForBES are net of harvesting costs and harvest losses and are thus reported as net realisable volume (NRV).

3.7.3. Model Infrastructure and Objectives

The model was originally based on an Excel platform which had transposed the FC static yield models from their paper format into digital worksheets providing yield information on which a forest extension tool (Forest Investment and Valuation Estimator (FIVE)) was based. FIVE was developed incrementally by the authors and has been piloted and validated in the field over a number of years in conjunction with forest extension colleagues from the Teagasc Forestry Development Department. In order to accommodate the wider range of objectives required by this research FIVE was further developed and transposed to a format which would allow for greater modelling flexibility both historically and into the future. The additional computational power required is provided by STATA software.

Having examined the theoretical aspects of both agronomic growth and financial valuation and taking on board the range of methodologies presented in the scientific literature, we arrive at the most relevant scenarios to be examined i.e.:

・ assess the impact of site fertility and yield class on return

・ assess the impact of thin versus no thin scenarios

・ compare NPV’s with and without subsidies

We will compare the optimal biological rotation with the industry reduced rotation and the optimal financial rotation of maximum NPV. In addition, we would like to examine the sensitivity of the NPV calculation to:

・ a range of discount rates ranging from 1 to 7 percent; and

・ use of differentiated component specific price indices versus average CPI.

We would also like to be able to model decisions taken by farmers historically as well as into the future, so we develop a cohort bio-economic model where each year from 1984 to 2013 is an individual cohort in the model, thus allowing us to generate life-cycle growth, cost and incomes streams for each cohort.

Table 3 presents a summary of the data sources and assumptions used in building the ForBES model to generate growth, cost and revenue curves for the required scenario and sensitivity analyses. Cost streams are generated for each year using both average and component specific CPI. Revenue streams are generated for each year, by yield class by applying price size curves of Irish price data to timber yields for thin and no-thin options on an annual basis. Subsidies are included in income streams in the early years. Cost and revenue streams are discounted to generate NPV’s. These values are then converted to annual equivalised NPV’s and are calculated for single and multiple rotations.

The additionality provided by the ForBES model over and above the reviewed BEM’s lies in the computational power and flexibility built into the model to assess financial impacts across the entire afforestation system, giving us the capacity to:

・ run iterative rotations for each species and yield class from 30 to 50 years to determine the optimum NPV.

・ run sensitivity analysis of results.

・ provide for the inclusion of agricultural opportunity costs and historic forest subsidies in generating NPV’s.

4. Results

In this section we want to assess the sensitivity of the results in ForBES to methodological and forestry management choices and to assess differences in optimal rotation lengths for different optimisation criteria. We report the results for establishing a Sitka spruce forest in one year (2015) across a range of yield classes.

4.1. Life-Cycle Costs and Incomes

The life-cycle pattern of cumulative costs and incomes over one rotation for Sitka spruce (SS) for yield classes 14 to 24 is presented graphically in Figure 4. There is a substantial difference in the timing and magnitude of costs and incomes by yield class and by scenario.

Incomes and costs are similar across scenarios before the impact of thinning is evident. In relation to costs, establishment and maintenance of the forest for the initial four years is largely offset by the afforestation and maintenance grants and is therefore essentially budget neutral. Once forests are established and have undergone initial maintenance works, costs for both thin and no-thin scenarios increase only by the amount of annual maintenance and insurance charges. The largest impact is the reforestation cost which is included as a cost in the first rotation. We do not see a difference by yield class as both establishment costs and grants and subsidies are budget neutral.

Income begins to vary by yield class and by thinning decision at age of first thinning. Intermediate income from thinnings is small in early thinnings but grows rapidly as the rotation approaches clearfell. The largest impact on cumulative income is the income from clearfelling, which increases incrementally across the yield classes. The “jump” in income between yield class 18 and 20 in the thin scenario bucks this trend. This jump is reflective of an increase in rotation age from age 42 at yield class 20, to age 45 at yield class 18. By contrast, the no-thin clearfell age decreases almost incrementally with increasing yield class.

4.2. The Sensitivity of Net Present Value (NPV) to Scenario Choice

To test the robustness of conclusions, we present the results of the sensitivity of the calculation of NPV to different management and methodological scenarios. Due to the complexity of the model and the size of the dataset, we run the sensitivity analysis on the 2015 data. Results are expressed as annual equivalised (AE) values of the NPV.

The baseline discount rate chosen is 5 percent (Clinch, 1999) incorporating an interest rate of 3 percent and a risk premium of 2 percent. As expected, the AE increases (in Table 4) with yield class for both thin and no thin scenarios, reflecting the higher productivity of higher yield classes. Yield class 24 generates an AE value that is 59 percent higher than for yield class 14. In general the AE gap between thin and no thin scenarios rises with yield class from a lowest gap for yield class 16 of less than 1 per cent to a gap of over 8 per cent for yield class 24 as a result of the additional income from thinning.

Figure 5 reports a sensitivity analysis for a range of discount rates from 1 to 7 percent. The economic return varies hugely with discount rate. There is a lower difference between yield classes when we use a higher discount rate as the largest differences between yield classes result from clearfelling, reflecting the lower weight that is placed on revenues arising far into the future. It also reflects the motivation behind the payment of upfront subsidies as income received today is more highly valued than future income.

The annual subsidy (forest premium payment) for Sitka spruce (10 percent diverse) is substantial at €5 10/ha for 15 years. In line with a priori expectations, yield class is very important. The inclusion of forest premium in

Note: species: sitka spruce; year: 2015; discount rate: 5%; with premium; for one rotation, average CPI.

Table 4 in the calculation of the NPV has a large positive effect on forest returns, with the gap much higher on lower yield classes. The AE for yield class 14 increases by a factor of 5 for the thin scenario and by a factor of 7 for the no thin scenario. This tails off to a doubling of the AE for yield class 24 for both thin and not thin scenarios. This reflects the fact that subsidy payments do not vary by yield class, while productivity varies a good deal. Thinning thus has a larger impact on improving forestry productivity on poorer land.

The opportunity cost of planting former agricultural land also depends on the agronomic characteristics that are correlated with yield class. From these results it would appear that the impact of the observed variability of AE in relation to subsidies is that it disproportionally incentivises planting on poorer quality land.

When we compare forestry outputs with the opportunity cost of planting using other data sources, we need to adjust for differences in price across time. The sensitivity analysis around the use of price indices presented in Table 5 shows that there is a considerable difference in annual equivalised NPV when using differentiated rather than average indices. In other words the weight of inputs used for forestry is different to the weights used in the CPI and so the price index is different. Across thin and yield class scenarios, the AE values using the component specific indices are lower than the AE values generated using the general consumer basket. The AE also varies by thin/no thin scenario and by yield class. The impact is small but linear and we believe it is worth considering using component specific CPI’s in future analysis, as it allows for greater flexibility and accuracy in predicting future returns, particularly in relation to comparing forest and agricultural returns.

4.3. Optimal Rotation Length

The main focus of this analysis is to compare the optimal rotation length between biological optimization and financial optimisation. In the former we utilise the highest MAI generated using the FC static yield model. In the latter we use the year in which the highest NPV is generated by ForBES as a result of running iterative rotations.

In Table 6 we see that the rotation of max MAI ranges from 58 to 48 years for the thin scenario and from 53 to 48 years for no thin scenarios. We see that the age of max MAI reduces with yield class and that at lower yield classes, the thin scenario takes longer to achieve maximum MAI than the no thin scenario. This is due to

Note: species: sitka spruce; year: 2010; discount rate: 5%; with premium; for one rotation, average CPI.

Note: species: sitka spruce; year: 2015; discount rate: 5%; with premium; for one rotation, average CPI.

the interruption in growth and cumulative volume production as trees react to the “shock” of thinning before reverting to typical growth patterns.

In practice in Ireland, a reduced rotation length has been adopted by the industry as a means of accounting for faster growth rates in Ireland than in Britain for some conifer species (Anon, 1977) . As the reduced rotation is based on the rotation of maximum MAI, there is a linear relationship between both rotations and they display similar trends. The biggest difference is the substantially reduced clearfell age. This reduction ranges from 12 years at yield class 14, to 11 years at yield class 16 and 18, to a 10 years reduction for higher yield classes in the thin scenario. In the no thin scenario, the reduction in rotation length ranges from 11 years at yield class 14 to 10 years for yield classes from 16 to 24.

In reality, the financial components of the NPV grow at different rates over time and are affected by the type of price indices used in the analysis. Therefore the optimum financial rotation varies over time if the components are not held constant. This justifies the need for a model such as ForBES which has the flexibility to conduct sensitivity analysis of other (new) management assumptions which can be updated regularly as new price information becomes available.

The financially optimum rotation age is determined at the point of maximum NPV of expected benefit/profit. We compare results including and excluding subsidies to assess whether the existence of a forestry subsidy changes the incentives in relation to management in terms of rotation length or whether it only affects the decision to plant or not.

Comparing the optimal financial rotation with the maximum MAI based rotation we find in Table 6 that there is a substantial difference between the optimal financial and biological rotations. The thin scenario rotation lengths vary from 50 years at yield class 14 to 43 years at yield class 24. The range of the no thin rotation lengths is considerably larger with a difference of 13 years between the lowest and highest yield class.

In comparison with the reduced MAI rotation lengths, the max NPV rotations are longer for all yield classes in the thin scenario with gaps ranging from 1 to 5 years. In the no thin scenario, the gap ranges from 7 years for the lowest yield class to being two years shorter for the highest yield class (24). Thus, the optimal financial rotations fall at a faster rate for the no-thin scenario than for the thin scenario. The differences are not linear, so we present the individual NPV’s graphically in Figure 6 to extract more information.

In focusing initially on the NPV inclusive of subsides, we note a number of features:

・ The magnitude of the NPV is considerably higher when subsidies/premium payments are included in the calculation.

・ The gaps between yield classes are much closer for the NPV including the premium than excluding the premium. Thus subsidies reduce the differential incentives, reflecting the fact that there is no explicit variation

between areas other than those areas defined as less favoured areas (LFA’s) (see Ryan et al., 2014 ).

・ The NPV curves for the thin scenarios are flatter in general than the no thin curves.

・ Despite this variation between the NPV’s which include and exclude premium, we find the same optimal rotation lengths. It is not clear whether this is a statistical artefact given that there are so many issues that affect it or whether it will always be the case. Particularly in the higher yield class situation, it is plausible that a small change in a driver might result in a large change in the optimal rotation length, given the flatness of the NPV curve observed relative to rotation length.

・ The thin NPV curves increase monotonically i.e. the age of maximum NPV decreases with increasing yield class. However, we note the non-monotonicity of the optimum rotation length curve for the no thin scenarios.⁵

Essentially this confirms that the main driver of the point at which the NPV is maximised is the discounted timing of the clearfell. Intuitively, this makes sense as the subsidies occur only in the early part of the rotation and the sheer magnitude of the clearfell value at the end of the rotation is a strong driver of the age of maximum NPV.

5. Conclusion

In this paper we describe the development of the Teagasc Forest Bio-Economic System (ForBES) to examine the financial impact of different measures and choices on the economic return to forestry in order to provide information to farmers and policy makers on the financial optimisation of afforestation and forest management decisions. Many of the BEM’s reviewed as part of this research address different dimensions of forest management decision making in great depth, however to our knowledge, ForBES is unique in the breadth of silvicultural and financial choices that it has the capacity to model across the whole afforestation system, enabling farmers to make better informed afforestation decisions. Reflecting the factors driving tree growth and the impact of management decisions on volume outcomes and building on the management choices in the literature, we selected a number of scenarios to allow us to investigate the financially optimum rotation. Simulating the scenarios for Sitka spruce we find that different objectives result in different outcomes. We see substantial differences between the biologically optimal rotation, the reduced rotation in common usage and the financially optimal rotation and find that the results are particularly sensitive to the choice of management and methodological assumptions. Specifically, we find that better site productivity and thin versus no-thin options result in shorter rotations across all optimisations, reinforcing the usefulness of this type of financial modelling approach.

ForBES potentially has the capacity to take inputs from dynamic growth models to reflect forest management decisions taken on the basis of market demands and pricing structures, rather than on the management regimes imposed by static growth models. The prediction of long-term timber revenues is currently limited by the lack of availability of Irish historical price data for timber assortments. Future availability of this information would allow for additional analysis of the sensitivity of the optimal financial rotation to timber prices. We could alsoadd to this information by developing confidence intervals around the data behind the curves, allowing for even more precise modelling of the financial optimum rotation.

The nature of the infrastructure developed in ForBES will allow for new scenario and sensitivity analyses as policies change over time. At present, the model currently generates outputs based only on net realisable timber volume, however ForBES has the capacity to include carbon sequestration from total forest biomass as a model output. At present this model is based on hypothetical forests but we ultimately want to scale up to the national level. This would hugely improve the role of ForBES as a farm afforestation decision support tool, providing important information for both farmers who are considering afforestation and for policy makers incentivising further afforestation.

Cite this paper

MaryRyan,CathalO’Donoghue,HenryPhillips, (2016) Modelling Financially Optimal Afforestation and Forest Management Scenarios Using a Bio-Economic Model. Open Journal of Forestry,06,19-38. doi: 10.4236/ojf.2016.61003

References

Appendix 1

Sources of Cost and Price Indices

Component Specific Indices

NOTES

¹dbh is measured 1.3 metres above ground level using a measuring tape.

²Thinning yield at MTI for a yield class 14 crop which will be thinned at 5 year intervals is 0.7 × 14 × 5 = 49 m³/ha (Kerr & Haufe, 2011) .

³Top height is the mean height of the 100 largest dbh trees per ha, measured by triangulating the angle to the top of the tree to give the height of the tree.

⁴A sequence of thinnings prescribed by FC models over the life of a forest stand.

⁵At first glance, this could be an anomaly, however when we examine the data behind the curves we see that it is caused by the flatness of the curves at this point. While the maximum NPV is achieved in year 39, from year 34 onwards, the NPV fluctuates between €8533 and €8649. However, we cannot draw further inferences about earlier clearfell ages without having confidence intervals around the data observations. This is currently not possible as there are no standard deviation values for the FC growth curves.