Open Journal of Acoustics
Vol.05 No.04(2015), Article ID:62124,21 pages
10.4236/oja.2015.54014
Development of Instrumentation for the Measurement of the Performance of Acoustic Absorbers
James Christopher Johnston1, Maria A. Kuczmarski1, Garth Olszko2
1NASA Glenn Research Center, Cleveland, OH, USA
2Cleveland State University, Cleveland, OH, USA

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 September 2015; accepted 20 December 2015; published 23 December 2015
ABSTRACT
In both fixed and rotary wing aircraft, the move toward lighter structures has resulted in an increase in structural vibration and interior noise. Porous materials have been proposed as acoustic absorbers to reduce this noise. This paper discusses the development of equipment at the NASA Glenn Research Center for characterizing the acoustic performance of porous materials: a flow resistance apparatus to measure the pressure drop across a specimen of porous material, and a standing wave tube that uses a pair of stationary microphones to measure the normal incidence acoustic impedance of a porous material specimen. Specific attention is paid to making this equip- ment as flexible as possible in terms of specimen sizes need for testing to accommodate the small or irregular sizes often produced during the development phase of a new material. In addition, due to the unknown performance of newly developed material, safety features are included on the flow resistance apparatus to contain test specimens that shed particles or catastrophically fail during testing. Results of measurements on aircraft fiberglass are presented to verify the correct performance of the equipment.
Keywords:
Acoustic Impedance, Acoustic Measurement, Acoustic Attenuation

1. Introduction
A common definition of noise is unwanted sound. A more precise technical definition of noise is a statistically random wave, which differentiates the part of a wave or signal that carries no useful information from the part that does. A blending of these two definitions can be used to describe noise as sound that is unwanted or interferes with other activity. Noise is a particular problem in aircraft, where the move toward lighter structures in both fixed and rotary wing aircraft has resulted in an increase in structural vibration and interior noise [1] . This noise can propagate to the ground and adversely affect communities surrounding airports. It can also adversely affect the passengers and crew inside the aircraft, since the noise can be high for extended periods of time. Engine and gearbox noise are transmitted into the aircraft cabin through sound propagating through the air to the fuselage walls and through vibration energy propagating though the structure itself. While vibration in the structure can be a concern at a wide range of frequencies, acoustics concerns itself with frequencies in the range perceptible as sound. The range of human hearing is typically quoted as 20 - 20,000 Hz [2] , with the range 512 - 2048 HZ being critical to intelligibility of human speech [3] . A relatively small amount of noise in this critical range has a major impact on speech intelligibility. In order to increase the ability of those in an aircraft cabin to understand each other, methods of decreasing the noise in the cabin must be found. Aircraft typically uses fiberglass or polymer foams as acoustic insulation in the cabin, but these materials have disadvantages in environments where they may be exposed to common fluids (water, fuel, hydraulic fluid, etc.) that tend to fill the open porosity, thus preventing them from absorbing acoustic energy, dramatically increasing their weight, and potentially degrading them chemically. In addition, they suffer in their ability to provide repeatable performance when removed and replaced during maintenance due to mechanical damage incurred during handling. More advanced porous materials have been proposed as acoustic absorbers to decrease the amount of sound energy radiating into the crew cabin while meeting these secondary requirements.
Porous acoustic absorbers are typically composed of both a solid frame into which energy can be transferred and a fluid in the pores is formed by the frame. Pressure waves need to be able to penetrate the material in order to interact with it. Acoustical energy contained in these pressure waves can be converted into heat by viscous shearing of the fluid in the pores, as well as friction of the fluid as it moves past the solid frame. This heat can be transferred by conduction into the frame. In addition, acoustical energy can be transferred through physical deformation of the solid frame in response to fluid movement and impact of the pressure wave. For a material to be an effective acoustic absorber, the pores of the material must be large enough and the structure opens enough for the sound waves to penetrate into the structure to allow multiple interactions to occur. If there is too little interaction (the resistance to flow is too low), the pressure wave moves through the material with very little energy absorption. If the resistance to flow is too high, the pressure wave reflects from the front surface of the specimen without being absorbed.
One of the first characteristics used to evaluate a porous material for its performance as an acoustic absorber is its flow resistance, which is the pressure drop across a specimen as a function of the flow rate of the air moving through it. This is often used as a “gateway test”―materials with poor flow characteristics perform poorly as acoustic bulk absorbers. Several schemes exist for the measurement of the flow resistance of a porous specimen. One of the simplest is to enclose the specimen in a tube and blow air through it at a known rate, measuring the pressure drop across the specimen. Measurement of the volumetric flow rate and the pressure drop across the specimen allows determination of the airflow resistance, specific airflow resistance, and airflow resistivity [4] :
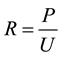 (1)
(1)
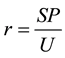 (2)
(2)
 (3)
(3)
where:
R = airflow resistance (mks acoustic ohm (Pa∙s/m3))
P = air pressure difference across specimen (Pa)
U = volumetric flow rate (m3/sec)
r = specific airflow resistance (mksrayl (Pa∙s/m))
S = area of specimen (m2)
r0 = airflow resistivity (mksrayl/m (Pa∙s/m2))
T = thickness of specimen (m)
Low flow resistivity measurements, indicating little air passes through, make a material unsuitable for acoustic applications. Otherwise, the acoustic impedance of the material needs to be determined to further characterize its acoustic performance. When sound impinges on the interface between the surrounding air and a material, a portion of the acoustic energy is reflected from the surface, a portion is absorbed, and the rest transmitted through. Most impedance measurement techniques place a massive reflective surface behind the specimen that reflects the transmitted energy back through the specimen. Measurements of the total reflected energy at the specimen surface, including energy reflected back through the specimen, are used to determine a reflection coefficient, which is then used to calculate the acoustic impedance or the specimen.
The standing wave tube is commonly used for measuring the acoustic impedance of test specimens. A specimen is placed into one end of a cylindrical or rectangular tube with a sound source at the other. The specimen is excited, either by a tone (single frequency) or by noise (multiple frequencies), and the sound field in the tube is sampled, typically with one or more microphones. One of the earliest experiments of this type makes use of a Kundt’s standing wave tube [5] , which is a transparent tube with a dusting of fine powder on the interior. Excitation of the column of air in the tube by a standing wave results in the powder gathering at points along the tube that represent the antinodes of the standing wave. The distance between these concentrations of powder allow the characteristics of the standing wave to be examined.
When a tone is used for excitation, a microphone placed inside of the tube can be moved down its length, sampling the amplitude of the standing wave formed in the tube and locating the positions of the maxima and minima. This technique, described in ASTM standard C 384-04 [6] , is capable of great accuracy but is time consuming. While it can now easily be made more efficient through automation of the microphone motion and signal acquisition, an even quicker technique uses several microphones placed at fixed locations. In the common two-microphone techniques, the microphones are placed between the sound source and the specimen. The area behind the specimen is terminated with a solid wall, which may be in direct contact with the back of the specimen, or include a gap of known length, depending on the details of the experiment. Both the ASTM E1050-08 [7] and the ISO 10534-2 standards [8] describe an impedance tube where the specimen is in direct contact with the terminator, two fixed microphones a known distance apart are used, and the distance from the closest microphone to the face of the specimen is known. The interior dimensions of the tube, microphone spacing, and the distance from the specimen face to the nearest microphone determine the range of frequencies that can be tested in the tube. The interior dimension that determines the characteristics of the tube is the diameter for round tubes and the length of the longest side for square or rectangular tubes. These techniques rely on the sound waves in the tube being planar. Because higher modes can propagate as the excitation wavelength approaches the size of the internal cross-section of the tube, both the ASTM and ISO standards define an upper frequency for a tube in relation to this dimension. Assuming a tube with a circular cross-section, the internal diameter is used and the upper usable frequency, fu, is defined as:
 (4)
(4)
where:
fu = upper usable frequency (Hz)
c = speed of sound (m/s)
d = tube diameter (round tubes), largest section length (rectangular tubes) (m)
K = 0.586 (ASTM) or 0.58 (ISO) (round tubes)
The K term is used to insure that the upper frequency stays well away from the condition where the excitation wavelength approaches the tube diameter. For square or rectangular tubes, the form of the equation for the upper frequency limit remains the same, but a K value of 0.5 is used and the largest section length is used in place of the diameter. An additional constraint is made on the aspect ratio of rectangular tubes, where ratios greater than 2:1 or less than 1:2 are discouraged, with 1:1 being preferred. At least three tube diameters are required between the sound source and the nearest microphone to allow any non-plane waves generated by the sound source to dissipate.
The spacing between the microphones and the distance from the specimen face to the nearest microphone also constrain the performance of the system. The microphone can be within one half of the tube diameter for specimens with smooth surfaces but must be moved farther away as the surface becomes rougher or more irregular to insure that it samples plane wave radiation rather than higher order modes induced by the shape or surface irregularities of the specimen. A larger spacing between the microphones increases accuracy but limits the range of frequencies that can be tested. According to the standards, the microphone spacing must be smaller than the half wavelength of the highest frequency of interest. The maximum spacing, s, is defined by the ASTM standard as [7] :
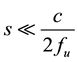 (5)
(5)
With the recommendation that the spacing not exceed 80% of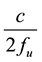 . The ISO standard defines it more specifically as [8] :
. The ISO standard defines it more specifically as [8] :
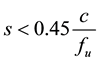 (6)
(6)
Combining (4) and (6) yields:
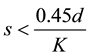 (7)
(7)
The standards also state that the microphone spacing should be greater than 5% of the wavelength of the lowest frequency of interest [8] :
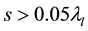 (8)
(8)
The wavelength is given by:
 (9)
(9)
Combining (8) and (9) yields:
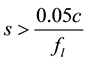 (10)
(10)
Combining (4) and (10) yields:
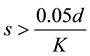 (11)
(11)
For Equations (5)-(11):
s = microphone spacing (m)
c = speed of sound (m/s)
fu = upper usable frequency (Hz)
fl = lower usable frequency (Hz)
λl = wavelength at lowest frequency of interest (m)
λ = wavelength (m)
f = frequency (s−1)
The microphone spacing range can now be expressed in two ways. By using (6) and (10), this range may be expressed in terms of the speed of sound and the frequency:
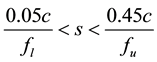 (12)
(12)
By using (7) and (11), the microphone spacing range may be expressed in terms of the tube diameter (or largest section length) and K:
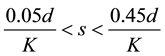 (13)
(13)
Once a tube diameter has been chosen, the upper usable frequency for that tube can be determined from (4). By using this frequency in (6), the maximum microphone spacing can be obtained. By using this spacing in (10), the lowest usable frequency for that tube can be determined. As an example, frequency limits for various tube dimensions of standard heavy wall pipe at 20˚C are given in Table 1.
These techniques generate a standing wave through the interaction of the incident and reflected waves coming from the terminator and measure the sound field at the two microphone positions simultaneously. The signal recorded at each microphone position is a combination of the incident signal coming directly from the sound source and the signal reflected from the specimen. The separation between the microphones allows the sound field to be sampled in two distinct places so the phase of the sampled signals will vary according to the frequency and the separation distance. The constraint that the microphone spacing be smaller than the half wavelength of the highest frequency to be used insures that the phase difference caused by the microphone spacing can never exceed π radians (180˚).
The data collected from the microphone pair is processed to determine the transfer function between their locations, most commonly using the equation [7] :
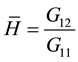 (14)
(14)
The cross power spectrum is calculated by multiplying the complex sound pressure at position 2 by the complex conjugate of the complex sound pressure at position 1. The auto power spectrum is similarly calculated by multiplying the complex sound pressure at microphone position 1 with its complex conjugate:


In (14) - (16):







The raw microphone data is in the time-domain, measured as a series of voltages and collected with a constant time interval between them. The form needed for the transfer function calculation is in the frequency domain― signal vs. frequency. Frequency domain pressures for each microphone position are obtained by performing a Fourier transform on the time-domain data collected at that position.
In order to reduce the noise level in the complex pressure data, several data sets can be taken for each microphone position and averaged. If the excitation source is a single tone and data collection can be synchronized with the phase of the excitation signal, the data can be averaged in the time-domain. This provides several efficiencies: the amount of raw data that it is necessary to store is much smaller, since the average of N data sets requires the same amount of room as a single data set, and the computational time is reduced, since the averaging process requires fewer and simpler calculations than the fast Fourier Transfer (FFT) procedure does. When time-domain averaging can be done, the resultant data set needs to be Fourier transformed only once. In contrast, if the excitation source is random or if the start of data acquisition is not phase-synchronized with the excitation signal, time-domain averaging can’t be used. In this case, each time-domain data set is Fourier transformed
Table 1. Dimensions and frequency limits for common heavy wall pipe sizes (c = 343.6 m/sec, K = 0.58).
individually, either immediately after data collection or in a subsequent step operating on stored data. The results of the FFT calculations are then averaged to provide the transfer function.
In any case, the time-domain data, whether individual or the result of the averaging process must undergo some manipulation before the FFT is performed. The FFT assumes that the data is infinite, so the abrupt transitions at the beginning and end of a finite data set result in artifacts in the processed data. A windowing function that smoothly forces the beginning and end of the collected time-domain data to zero removes these artifacts. The Hanning window is recommended in the ASTM standard [7] , applying a “shifted cosine” function, illustrated in Figure 1, to smoothly force the magnitude of the collected data to zero at the extreme ends.
The Fourier transform will deliver a complex frequency-domain spectrum showing the relative contribution of each frequency contained in the original data. The resolution of frequency-domain spectrum is dependent upon the sampling rate and the number of samples used in the time-domain data. The sampling rate defines the Nyquist frequency, which is, by definition, half of the sampling frequency (to observe a signal of frequency x you must sample at a frequency of at least 2x). It is the highest frequency that can exist in the data set without undergoing aliasing [9] . Aliasing occurs when the sampling rate is too low to properly characterize the frequency being sampled. For frequencies below the Nyquist frequency, there are at least two samples per period. Above the Nyquist frequency, the sampling period is greater than the period of the signal being sampled, leading to an incorrect calculation of the frequency. Frequencies in the data set above the Nyquist frequency appear in the frequency-domain spectrum at lower frequencies reflected around the Nyquist frequency. For example, a frequency 100 Hz higher than the Nyquist frequency will appear in the frequency-domain spectrum as a peak 100 HZ below the Nyquist frequency.
The FFT algorithm generates a frequency-domain data set that contains half of the number of points as were in the input data set. The combination of the number of points in the frequency-domain data and the Nyquist frequency set by the sampling rate allow the frequency resolution of the transformed data to be calculated.
For a time-domain data set consisting of 2048 data points sampled at 8000 Hz, the resultant frequency-domain spectrum has 1024 separate frequency “bins” representing the range from 0 to 4000 Hz. The resultant frequency resolution is therefore 3.9 Hz per bin. All of the signals that fall within a single bin are lumped together and cannot be further resolved. In the Fourier transform, a constant added to the input data has the effect of adding a signal at 0 Hz and results in a peak at the low frequency extreme of the transformed spectra. In a perfect system all of the components would generate an output of zero when presented with an input of zero. This rarely happens in a practical system, so in this experiment the “DC peak” typically represents the combined offset error of the microphone, amplifier, and data acquisition system. The effect of such an offset is to shift the average of the time-domain data away from zero. In this experiment, since we are expecting the excitation and sampled signals to be composed of sine waves, a simple average is calculated and the value of the average subtracted from each
Hanning Window
Figure 1. The Hanning window.
data point in the set. This simple DC correction adjusts the data to make it center at zero, eliminating the contribution of a constant offset in the data. Because sinusoidal signals really only average to zero over an integral number of waves, this simple technique has the potential to introduce an offset of its own. In practice, with the equipment described, this has been only rarely observed and more sophisticated DC correction schemes appear to offer few advantages.
The use of two microphones introduces a potential source of experimental error [10] . The tacit assumption is made that the microphones have identical phase and amplitude responses. In other words, the only difference between the phase and amplitudes of the sampled signals should come from the fact that they are sampled at different places in the sound field. This is not true in practice. Variations in the amplitude or phase response of the microphones relative to each other will appear as if there were differences in the sound field. In addition, it is possible that the position of the acoustic center will vary between microphones, changing the effective spacing between them. One method to compensate for these differences would be to generate phase and amplitude corrections for each microphone and apply those corrections to the raw data before further processing. The question of how well this can be done or how often it needs to be done is left open in the literature and, in practice, this approach appears to be rarely used. While it is possible to fully characterize the microphones to allow these errors to be compensated for, a simpler and more common way to attack this issue is to switch the physical positions of the microphones during the experiment. If care is taken to ensure that the microphones occupy the same position in either orientation (the distances from the surface of the specimen to the center of the near and far microphones are the same in both orientations), a calibration factor can be calculated that removes the phase and amplitude differences between them. The correction is calculated through [7] [8] :

where:



Once this correction factor has been calculated it can be applied to correct subsequent data [7] [8] :

where:
H = corrected transfer function (dimensionless)


Once the transfer function is known, the complex reflection coefficient can be calculated [7] [8] :

where:
R =the complex reflection coefficient (dimensionless)
H = the corrected transfer function (dimensionless)
k = the complex wave number (m−1)
s = distance between microphones, center to center (m)
l = distance from the test specimen to the center of the nearest microphone (m)
The wave number, k, is often treated as a real number for simplicity, but is more properly complex, with the imaginary part representing the attenuation constant of the tube.
The real part of the wave number is defined as [7] [8] :

where:

f = the frequency (Hz)
c = the speed of sound (m/sec)
When the distance between the specimen face and the nearest microphone exceeds three times the tube diameter, the attenuation due to losses in the tube becomes too significant to ignore. In that case, an imaginary term is added to the wave number to account for the losses. This attenuation constant can be measured experimentally using the moving microphone method discussed earlier or one of a number of calculated corrections can be applied. The ASTM [7] and ISO [8] standards use the same estimation equation with different scale factors:


where:

f = frequency (s−1)
c = speed of sound (meters/sec)
d = tube diameter (meters)
The normal incidence sound absorption coefficient, a, and the normal specific acoustic impedance ratio
can be calculated from the reflection coefficient [7] [8] :


where:
a = normal incidence sound absorption coefficient (dimensionless)
R = complex reflection coefficient (dimensionless))

The characteristic impedance of the air, 

where:



The real term represents the resistance to air flowing through the specimen. It is not frequency dependent and should match the results measured in the flow resistance experiment. In practice, the values obtained through the two techniques often do not match. The oscillating particle velocity within the specimen measured in the impedance experiment is not the same as the steady air velocity in the flow resistance experiment, which is measured in the air stream outside of the specimen [4] . The imaginary part of the impedance is the reactance, which is frequency dependent.
A more complex version of the impedance tube was described by Song & Bolton [11] . This tube uses four microphones, two on each side of the specimen to measure transmission loss. In this case, an approximately anechoic termination is used beyond the additional two microphones, with the intent that any sound transmitted through the specimen be absorbed in the terminator rather than reflected. Because this experiment shares the phase and amplitude error issues between microphones that were identified in the ASTM experiment, but now with four microphones instead of two, and because there is no obvious way to interchange microphones to eliminate these errors, this experiment uses the same microphone sequentially in each of the four microphone positions. Details of this method may be found elsewhere [11] . It is of interest to note that in this and other acoustics papers, the complex amplitudes contain the term 
2. Description of Apparatus
2.1. Flow Resistance
The flow resistance apparatus blows air through a specimen at a controlled rate and measures the pressure drop across the specimen. The tube constructed at NASA GRC uses a laminar flow element to measure flow rate. A schematic is shown in Figure 2. The flow element is equipped with two pressure sampling ports.
It provides a predictable pressure drop across the sampling ports proportional to the amount of flow through the element. Measuring the pressure drop across the sampling ports (in this case, using a transducer with a maximum differential pressure range of 10” of water at 4˚C (2490.9 Pa, 0.3613 psi) allows the flow through the apparatus to be measured. The range of the transducer exceeds the calibrated range of the flow element, allowing flows to be measured through the entire 0 - 0.01888 m3/sec (0 - 40 CFM) range.
The inlet end of the flow element is connected to the air supply system with a 0.6096 m (2’) length of 2” schedule 40 pipe (0.06039 m OD, 0.05250 m ID (2.3775” OD, 2.067” ID)). The outlet end of the flow element has an identical length of pipe, with the inlet half of the specimen holding system at the end. The inlet half of the specimen holding system is comprised of a pipe flange with a pair of custom-machined adaptor rings attached that are used for holding the test specimen. A series of bolts with long coupling nuts attached provide a mechanism for connecting the inlet half to the back half of the holder, trapping the specimen between them. This is illustrated in Figure 3. The specimen holder is fastened with a set of free-floating bolts whose lengths are selected based on the thickness of the specimen. The back half of the specimen holder is terminated with a 0.1524 m (6”) length of 2” schedule 40 pipe. Two drilled and tapped holes were made in the tube about 0.0762 m (3”) before the specimen holder and an identical hole was made in the short tube about 0.0762 m (3”) after the specimen holder to allow connection to a set of pressure transducers.
The downstream port and one upstream port are used to monitor pressure across the specimen. Two differential pressure transducers are connected in parallel across the specimen, one providing high resolution over a very
Figure 2. The flow resistance apparatus.
Figure 3. Sample mounting arrangement for the flow resistance tube.
narrow pressure range and the other providing lower resolution over a much wider range. The high resolution transducer operates over a range of 0 to 10 inches of water at 4˚C (2490.9 Pa, 0.3613 psi) full scale. The high range transducer operates over a range of 0 to 150 psid (1034213.6 Pa) full scale (using units of inches of water at 4˚C is be common in the US for pressure transducers and manometers with a maximum range below 1 psi). A three-way solenoid valve is placed in the line leading to the upstream inlet of the high resolution transducer. This solenoid connects the transducer to the tube; when de-energized, it vents the transducer into the laboratory. This solenoid is operated under control of the data acquisition computer, isolating and venting the more sensitive transducer if it reaches or exceeds its full scale limit. The damage threshold for these transducers is approximately four times their maximum pressure, so this arrangement protects the sensitive transducer in the case of a specimen with extremely high flow resistance, where the tube pressure can spike rapidly. The remaining upstream port has a 150 psig pressure transducer attached that is used to monitor the pressure in the tube.
Air is supplied to the system from a regulator operating off of shop air. The outlet of this regulator passes through a manual needle valve, a solenoid valve, a proportionally-controlled valve, and into the tube. A tee is installed at the point where the air enters the tube. A solenoid-operated vent valve and a 50 psi spring-loaded relief valve are connected to the tee to provide a means of relieving pressure in the tube under computer control, as well as protecting the tube from exceeding the intended maximum pressure. Air flows through a series of adapters to transition the 1/2” Schedule 40 supply pipe (0.021336 m OD, 0.015799 m ID (0.840” OD, 0.622” ID)) to the diameter of the flow resistance tube.
The three solenoid valves operate under control of the data acquisition computer to provide protection for the pressure sensors and specimen. If the differential pressure across the flow element reaches the limit of the pressure sensor associated with it, the supply solenoid closes, stopping airflow into the tube, and the vent solenoid valve opens, relieving pressure. If pressure across the specimen reaches the maximum range of the low pressure sensor, then the three-way solenoid valve disconnects the inlet side of the sensor, venting it to the lab. The experiment can continue using the high-range sensor. The low range sensor will remain isolated until the pressure across the specimen drops below its maximum range, at which point the solenoid valve opens and the sensor is re-enabled. The turn-off pressure is higher than the turn-on pressure, providing some hysteresis to prevent the valve from opening and closing rapidly when the pressure is near the limit. The system inlet solenoid can also be shut off when the pressure nears a predetermined limit in order to protect the specimen. Without this protection, a specimen with very high flow resistance will cause a rapid pressure rise behind it, which can cause it to shatter. When this happens, pieces of specimen are blown out of the tube and into the laboratory. For this reason, a vacuum-assisted particle scavenger hood was designed. This is shown in Figure 4. This hood, when fitted to the end of the tube and attached to a shop vacuum with a HEPA filter installed, is capable of processing all of the air flowing out of the flow resistance tube and will serve to trap particulates released by the specimen. When no air is flowing through the tube, the gap between the hood and the tube provides sufficient air flow to allow the vacuum
to operate normally. Computational Fluid Dynamics (CFD) modeling of this hood assembly demonstrated that the operation of the vacuum-particle safety system will not adversely affect the ambient pressure at the reference port for the differential pressure gauges across the specimen.
2.2. Acoustic Impedance
Two acoustic impedance tubes have been constructed at NASA GRC. They are designed to be modular, allowing the selection of the ASTM/ISO [7] [8] two-microphone impedance experiment or the 4-microphone Song & Bolton (S & B) experiment [11] . These are shown in Figure 5. The modularity of the system allows other experiments to be implemented as necessary.
In both tubes the acoustic driver and the initial 2-microphone module are shared between ASTM/ISO and S & B modes. When configured in the ASTM/ISO mode, the tube is terminated with a solid aluminum plug. In the S & B mode, an additional length of tube including mounts for an additional pair of microphones is added after the specimen holder and is then terminated with a length of closed tube loosely packed with fiberglass to form an approximately anechoic termination.
One tube is round, nominally 2” in diameter, while the other tube is 2” (0.0508 m) square. This provides greater flexibility in specimen preparation and avoids the compromises necessary to attempt to mount a square specimen in a round tube and vice versa. Both systems share the same audio generator, power amplifier, microphone amplifier, data acquisition system, and computer. The microphone amplifier has four channels, allowing pairs of microphones to be dedicated to each tube or additional microphones to be used in an experiment. The proper tube is then selected in the software to convert from one to the other. Provisions for a third microphone
Figure 4. Particle scavenger hood.

Figure 5. (a) 2” round impedance tube in 4 microphone S & B mode. (b) 2” round impedance tube in 2-microphone ASTM configuration.
holder have been added to the tubes in the vicinity of the specimen face to allow more uniform sound power levels to be applied to the specimen.
The round tube is made from 2” schedule 80 PVC pipe (0.060325 m O.D., 0.04925 m (2.375” O.D., 1.939” I.D.)), connected with standard solvent weld flanges and unions. A set of custom-machined mount rings form a specimen holder compatible with 2” schedule 80 pipe. The mount rings are 0.0813 m (3.2”) outside diameter and 0.0127 m (0.5”) thick. They have been bored through to match the I.D. of the schedule 80 tubing. Each face has been bored 0.003175 m (0.125”) deep to the O.D. of the Schedule 80 tubing. These insets provide both a place where the ring can be adhesively mounted to the tube and for a specimen holder to be attached. The auxiliary microphone tube used in the Song & Bolton experiment has an identical ring attached. Each of these rings has holes drilled 120˚ apart for attachment of a set of 3/16” steel rods used to hold the main tube, specimen, and terminator (or secondary tube) together. The solid terminator used in the ASTM/ISO experiment is machined with an inset identical to the one on the mounting ring and also has the three holes for the mounting rods. The initial concept for specimen holders for this instrument was to use lengths of 2” Schedule 80 aluminum pipe. These simple holders are in common use with this system, and the specimen holder design created for use in the flow resistance tube was adapted for use with the impedance tube. Two variations on this design were constructed, one designed as a tube with a hole passing through the holder and the other with a solid aluminum plug allowing the holder to do dual duty as specimen holder and termination plug. Both are drilled to accept the mounting rods. The inner diameter of the holder is approximately 63.5 mm (2.5”) and the usable depth is approximately 19.5 mm (0.75”) Masking rings are used to fill any difference between the height of the specimen and the depth of the holder. These rings have in internal diameter of 49.25 mm (1.939”) to match the internal diameter of the tube. These unique specimen holders present their own compromises in the impedance measurements as there is a small volume specimen material of larger diameter behind the spacer rings, any radial misalignment of the rings will expose some of the ring to the sound field, increasing the observed reflection, but those compromises were judged to be acceptable in order to gain the capability to test specimens that cannot be manufactured to the precision necessary to fit the simpler and more efficient cylindrical holders.
The sound source for this system is an acoustic driver that is mounted in a custom machined PVC plug made to fit snugly to a 2” schedule 80 tube. This plug was drilled and tapped to match the threads on the nose of the acoustic driver. As originally designed, the driver was mounted to a flange and connected to a matching flange on the primary microphone tube with a layer of intervening padding to attempt to prevent flanking vibrations from traveling through the tube walls to the microphone. An anomaly seen in early data in the vicinity of 1 KHz led to the realization that the length of the tube from driver to specimen was approximately the wavelength of 1 KHz sound. The tube was reconfigured and lengthened to making its length equivalent to the wavelength of a tone below the 500 Hz lower limit of the driver. The connection between the main microphone tube and the acoustic driver tube is now made with a flexible rubber collar.
The square tube is made from 0.0635 m (2.5”) square aluminum tubing with 0.00635 m (0.25”) walls, yielding internal dimensions of 0.0508 m X 0.0508 m (2” X 2”). It uses an identical acoustic driver to the round tube. In this case, a 0.1524 m (6.00”) long aluminum tube, 0.03175 m I.D. X 0.0508 m O.D. (1.250” I.D. X 2.00” O.D.), was drilled and tapped to match the threads on the driver and an internal taper machined into the other end. A series of grooves were machined into the outside of the tube to provide a tight mechanical grip between the silicone rubber and the aluminum. With the use of a custom-machined centering plug, the driver mounting tube was centered in a length of 0.0762 m (3”) square aluminum tube and the gap filled with Dow Corning Silastic J RTV silicone rubber. The 0.0762 m (3”) square tube has 0.00635 m (0.25”) thick walls, making it a close slip fit over the outside of the main 0.0635 m (2.5”) square tube. The silicone rubber is intended to provide a flexible isolation medium to prevent flanking vibrations. A solid aluminum terminator plug mounts on the other end of the main tube using a similar 3” X 3” collar and held to the main tube using 3/16” mounting rods similar to those used in the round tube. An identical mount system is used for the auxiliary microphone module.
2.3. Specimen Holders
The flow resistance apparatus was designed to allow specimens to be mounted in short (0.0127 m to ~0.1016 m (0.5” to ~4”)) lengths of 2” schedule 40 aluminum pipe. The round impedance apparatus had a similar specimen tube, using lengths of 2” Schedule 80 aluminum pipe. Specimen holders for the square impedance tube are simply lengths of the 0.0635 m (2.5”) square 0.00635 m (0.25”) wall tube used for the main body of the apparatus. The specimens are mounted in these sections, loaded onto the end of the main tube, and held in place by the collar on the terminator.
With many of the specimens of interest, it is hard to make specimens that are a tight fit into the specimen holders made from aluminum pipe, either because they shrink when they are made or because they are too fragile to trim to shape when made oversize. For this reason, one specimen holder was designed for the flow resistance rig that takes 0.0635 m (2.5”) diameter parts. This holder has a nose and tail piece with the same dimensions as 2” schedule 40 pipe. One end is fashioned into a cap, held to the body of the specimen holder by a series of cap screws. A specimen can be inserted within the cavity formed by removing the cap and the gap between the top of the specimen, and the bottom of the removable cap can be filled with a series of metal rings. This is shown in Figure 6. A series of similar specimen holders were constructed for the impedance rig. The walls of the nose and tail pieces were thickened to match 2” schedule 80 pipe. In one of the holders, the tailpiece was not bored out, leaving an approximately 0.0508 m (2”) long solid plug to serve as the terminator for the ASTM/ISO experiment. Because the impedance rigs operate in essentially ambient pressure conditions, the 6 cap screws used to close the specimen holder for the flow resistance rig were replaced by 3 cap screws and 3 holes to allow the 3/16” mounting rods to pass through. The holder is attached to the tube using three steel collars with thumbscrews, the holder being mounted on the rods and pushed up into the specimen ring on the main tube. The collars are then slid onto the rods and pushed tightly against the back of the specimen holder’s flange, aligning the holder to the tube and providing a tight fit.
2.4. Audio Electronics
Both impedance tubes use 8 Ohm Selenium D250-X acoustic drivers rated for approximately 150 watts, with a frequency response range of 400 - 9000 Hz. The attachment to the impedance tubes is made using the driver’s integral 1-3/8”-18 screw mount. Because acoustic drivers are known to have damagingly high power dissipation at low frequencies, leading to overheating and eventual failure of the driver, they are never intentionally driven below 500 Hz. The drivers for the tube in use are connected to an Audio Source Amp 5.1 Monoblock amplifier rated at 70 W into 8 ohms. The signal source that drives the amplifier originates in a Stanford Research Systems DS360 audio synthesizer. This synthesizer is in communication with the computer controlling the experiment through an IEEE-488 interface. The audio output of the synthesizer can be routed through an Applied Research and Technology Model 351 31 band monaural equalizer. The equalizer is primarily for use with broadband signals and it has very little application for single tone experiments. All analog signals from synthesizer to amplifier are carried over balanced XLR cables.
The microphones used in these systems are LinearX M31 measurement microphones. These are low-voltage electret microphones. They are connected to an amplifier designed and built in-house that provides adjustable gain and offset, as well as power injection for the microphones and the high pass filtering necessary to remove the DC offset inherent in the microphones output signal. This amplifier also drives the coaxial cable connecting the amplifier to the data acquisition system. The signals input to the data acquisition system are monitored on a

Figure 6. (a) Reflection and transmission sample mount with a simple cylindrical sample holder. (b) Cross-section diagram on the reflective sample mount.
Hewlett Packard 54510B digital oscilloscope. This is primarily for the convenience (and peace of mind!) of the operator as it allows direct observation of the signals returned from the experiment in real-time.
2.5. Data Acquisition Hardware
The audio signals are connected to a National Instruments PCI-6123 8-channel data acquisition board. This device is capable of simultaneous acquisition, ensuring that sampling delays between channels are negligible. The system is also equipped with a National Instruments PCI-6221 data acquisition board connected to a National Instruments SC-2345 signal conditioning chassis. The chassis is configured with thermocouple, analog voltage, and 4 - 20 mA process inputs, as well as digital relay and 4 - 20 mA analog outputs. These are used for reading ambient temperature, barometric pressure and humidity, the pressure transducers, and for controlling the solenoid valves and the proportional valve on the flow resistance apparatus. The audio synthesizer is controlled by the computer through a National Instruments GPIB-USB-HS USB to GPIB interface.
2.6. Data Acquisition Software
All data acquisition and processing is done using National Instruments LabVIEW software running under the Linux operating system [12] . For each of the implemented experiments, separate data acquisition and processing programs were written. The primary reasons for doing this are:
1) The ability to store unprocessed data so the processing programs could be modified and re-run against already collected data. Once the raw data was modified by zero-correction, windowing, or calculating the FFT, it could not be brought back to its unprocessed state if an error was found in the processing code.
2) The ability to handle large data sets without encountering memory limitations. The initial development was done using frequency-domain averaging, which entailed saving all of the raw time-domain data if criterion 1 was to be observed. These data sets can become quite large, and at some point would be too large to hold in memory during acquisition before processing could begin.
3) The ability to processes the data in more than one program. The data-acquisition phase of development was simpler than the processing phase, and during the initial phase of development, the processing was not working correctly. It was unclear whether the problem stemmed from the capabilities of the software of from our incomplete understanding of the process, so the ability to process in another program was a needed capability.
4) The ability to keep the size of the diagram for the main LabVIEW virtual instrument (VI) to a manageable size. LabVIEW is a graphical data flow programming environment where functions represented as icons are “wired together” on screen. This is a simple and powerful way to create a program, but increasing complexity in a program leads to complex diagrams.
While it is clear that the experiments described in the ASTM and ISO standards were the same, the ISO standard described a procedure where the microphone correction could be performed directly on the unknown specimen in addition to the procedure that calculated the correction using a standard specimen. For this reason, the programs that implemented the experiment using the standard specimen were referred to (and named) the “ASTM” experiment and the programs that implemented the experiment where the corrections were made with the unknown were referred to as the “ISO” experiment. The ASTM/ISO experiment envisions the use of noise as the excitation source rather than a single tone. While the use of noise has the advantage of acquiring data across the entire frequency range of interest simultaneously, it is more difficult to maintain consistent amplitude across the entire spectral range. The noise signal has to be modified to ensure that it does not contain frequencies above the maximum frequency of the impedance tube or below the minimum frequency of the driver or the tube. With a frequency source that generates white noise, a bandpass filter could be used, but a random noise signal requires frequency-domain averaging. The standards suggest the use of a pre-recorded noise signal so the same excitation signal can be used every time data is acquired, which should allow the use of time-domain averaging. Because an experiment that uses a single tone only gives information on that single frequency, a series of experiments must be performed, one tone at a time, to build up a complete picture of the acoustic performance of a material.
The systems at GRC have implemented what we refer to as a “tone step” procedure, where the ability for the computer to remotely control the audio generator is used to allow the single tone experiment to be repeated across a number of frequencies (The ASTM and ISO standards envision the use of noise as the excitation signal. To avoid experimental difficulties we have chosen to automate the performance of a series of single frequency experiments instead). The frequency is set, a series of data sets is collected and stored, and this process is repeated over the frequency range of interest. This also provides an opportunity to adjust the amplitude of the generator’s output to maintain a constant intensity level in the collected data.
Because of the additional steps inherent in the measurement and processing of the standard specimen, programs specific to the acquisition and processing of that data were also developed. There are a total of four programs that implement the “ASTM experiment” while only two are used for “ISO” and the “S & B” experiment. Because of the differences in the processing between the ASTM, ISO, and S & B experiments, a series of experiment modes were defined. These modes are written along with the raw data from the acquisition program so a processing program can immediately detect a mismatch between the type of data it is expecting and the data in the data set it has been given to process. These modes included separate modes numbers for ASTM and ISO experiments using noise as the excitation source and were further expanded when time-domain averaging was implemented.
Supporting all of these programs is a set of shared initialization files that describe the experiment modes, aspects of the impedance tubes, air properties, and specimen holders. These were used to ensure that every program that required such common data was operating with the same data. The “tubes.ini” file, for instance, define the name, geometry (round, square, rectangular), various dimensions, the maximum frequency, and the sampling rate in terms of frequency for each tube.
Code in LabVIEW is inherently modular, and most programs make heavy use of LabVIEW Virtual Instruments (VI) acting as subroutines. Besides serving to unclutter the diagram, this makes code reuse straightforward. Each VI has a front panel with user interface elements on it as well as the wiring diagram. These user interface elements―controls when used as data inputs to the VI and indicators when used as outputs―are also used to define the inputs and outputs for a VI. In most cases when a VI is called from another VI, the front panel never appears, but VIs can be configured to display their front panel when called and to close them when they exit. This capability is used in each of the impedance programs when their setup VI is called. Each of the data acquisition programs will ask the user to select the specimen holder and update, if necessary, the length of the specimen holder, the distance from the front of the specimen holder to the front of the specimen (the Front Specimen Inset), and the distance from the rear of the specimen holder to the rear of the specimen (Rear Specimen Inset). The user also selects the specimen tube in use, the number of averages to take, the spectrum size, and has the opportunity to include a note about the specimen. In the case of acquiring calibration data for the ASTM experiment, the user can select the step size for the excitation frequency and will be prompted for the name of a file to write the raw calibration data into. In the case of acquiring specimen data in the ASTM experiment, the user is asked to select the calibration file that will be used to apply the microphone correction. At this point the excitation frequency step size used to create the calibration file will be displayed, and the user is prompted for the filename for the new data file. When all of the setup data has been entered, the user pressed the “START” button and data acquisition begins.
The acquisition programs all begin by collecting the ambient temperature, barometric pressure, and relative humidity from sensors connected to the data acquisition system. The user is prompted to put the microphones into the forward position, and when that is complete, autoscaling begins. During autoscaling, the excitation frequency and initial amplitude is sent to the audio synthesizer and data collected from the microphones. The output amplitude of the synthesizer is adjusted to bring the larger of the two microphone signals to 7 volts (70% of full scale on the data acquisition board). This process is repeated for each of the excitation frequencies, yielding an array of synthesizer amplitudes, one for each excitation frequency. This autoscaling scheme adjusts the excitation power to guarantee that the microphones and preamplifiers are not driven past their clipping limits while providing a constant signal level from the microphones, but it does so at the cost of having a different sound intensity at the sample face for every frequency. The round tube has been equipped with an auxiliary microphone located as close to the specimen face as possible to allow the evaluation of a scheme that would provide constant intensity at the specimen without overdriving the microphones. Because of the modular nature of the software, such alternatives can be readily tested and evaluated.
When data collection begins, the amplitudes are used to configure the synthesizer, and data is collected from the microphones for each frequency. In the case of a calibration run, the user is prompted to put the microphones into the reversed position and data is collected at all of the test frequencies again, using the stored amplitudes. Once that is complete, the data is saved to disk and the program exits. When calibration data is processed, the program prompts the user for the name of the file that holds the raw calibration data, which is then opened, the data extracted for each excitation frequency, and a microphone correction file created. When specimen data is processed, the user is prompted for the name of the data file. Each data file contains a flag to indicate whether it is calibration or specimen data, as well as the path name for the microphone correction file. The specimen data is processed for each excitation frequency, the correction applied, and the reflection coefficient, absorption coefficient, and impedance calculated. The resultant data is written into both a text report file and a spreadsheet file.
3. Results and Discussion
One challenge presented in the measurement of flow resistance and impedance is the lack of standard specimens. ASTM publishes standard procedures for the measurement of acoustic impedance, but does not define a standard reference specimen whose absorption coefficient and acoustic impedance is known. To check our systems, a specimen of aircraft fiberglass (1” thick Johns Manville 9.6 Kg/m3 Microlite AA blanket) was supplied through the Structural Acoustics Branch at NASA LaRC, along with the results of their acoustic impedance testing. The absorption coefficient and impedance data for a series of fiberglass specimens measured at NASA LaRC is shown in Figure 7, Figure 8. At both power levels the spectra show much more pronounced run to run differences in the acoustic resistance than in acoustic reactance. Average values of the absorption coefficient, normal specific resistance and reactance were calculated from the LaRC data and used for further comparisons. The measurements made on fiberglass at NASA GRC are compared to the LaRC fiberglass averages, shown in Figure 9.


Figure 7. Measurements taken at NASA LaRC on Aircraft fiberglass samples at 120 dB (a) absorption coefficient, (b) resistance ratio, reactance ratio.


Figure 8. Measurements taken at NASA LaRC on Aircraft fiberglass samples at 140 dB (a) absorption coefficient, (b) resistance ratio; (c) reactance ratio.
The LaRC and GRC spectra are generally similar, with a broader run to run difference between resistance and reactance in the GRC spectra when compared to LeRC. The LaRC spectra show slightly higher resistance and reactance than the GRC spectra. Some of these differences can be attributed to the fact that the fiberglass was compressed somewhat in shipment.
The flow resistance of fiberglass is sensitive to the compression of the material. It is not clear that the unpacked and re-expanded material regained the same density as it had when originally tested. Two schemes have been used in the GRC instrument to set the sound power level applied to the specimens. In the first scheme, the audio generator output level is adjusted at each observation frequency to set the stronger of the two microphone signals to 6 V peak to peak (p-p), a level just below the point where the microphone/amplifier combination begins to clip. This has the advantage of always providing a signal exceeding the standard’s requirement that the signal be at least 10 dB above the background level but results in every test frequency being tested at a different excitation level.
The second scheme sets the audio generator output level to adjust the maximum response from either microphone across the range of frequencies to the 6 V p-p target used in the first scheme. For example, if the strongest signal observed in the system occurs at 1250 Hz on microphone 2, the signal generator amplitude is set to deliver a 6 V p-p signal on microphone 2 at 1250 Hz. That amplitude is then applied to the signal generator for all other test frequencies, guaranteeing that the data acquisition system will see an in-range signal throughout the


Figure 9. Comparison of measurements taken at NASA LaRC and GRC on aircraft fiberglass samples (a) absorption coefficient; (b) Resistance ratio; (c) reactance ratio.
experiment. For some signals, particularly at the high frequency end of the range, this may deliver signals that do not meet the criterion in the standard that the observed signal be at least 10 dB above the background.
It was hoped that the inclusion of a reference microphone near the specimen surface would provide a measurement of the sound power at the specimen so the signal generator could be adjusted over the course of the experiment to maintain a constant excitation level. Both computational analysis and experimental tests with the reference microphone have thus far failed to provide a scheme allowing the power level to be monitored and regulated across the entire frequency range using a single reference point. In addition, the larger 2.5” diameter specimen holder with the masking rings presents some acoustical compromises as it has diameter changes in the specimen region that are not anticipated by the standard. This design was originally developed for the flow resistance experiment; it was adopted for the impedance experiment because some of the materials that were to be screened in this experiment could not be reliably made or trimmed to fit the standard specimen holder. Both of these factors contribute to differences between the results.
A specimen of commercially obtained unreinforced silica aerogel was examined in the 2” square tube. This material, with a reported density of about 0.1 g/cc was extremely fragile and represents the extreme limit of the materials that this system would be required to screen. This material is fragile enough that it was a challenge to load it into the specimen holder without damage. This specimen demonstrated the high reflection coefficient and subsequent low absorption coefficient expected of a material with extremely high flow resistance, as illustrated in Figure 10. It was not screened in the flow resistance apparatus as previous attempts to perform flow resistance


Figure 10. Acoustic sopectra os a commercial silica aerogel sample (a) absorption coefficient; (b) resistance ratio; (c) reactance ratio; (d) reflection ratio.
on significantly stronger reinforced aerogel monoliths resulted in catastrophic failure of the specimen before any data could be obtained.
4. Conclusions
These test rigs were developed to perform rapid screening capabilities for a series of materials development projects with the intention of passing materials that looked good in the initial screening to more detailed acoustic testing at NASA LaRC. As a result, the emphasis was put on making these instruments as versatile, simple, and safe to use as possible. The modular design came out of the need to build a versatile instrument that could be adapted to the differing needs of various materials development programs. The custom LabVIEW software developed for these experiments was highly modular, allowing for versatility but also emphasizing ease of use for the operator.
The unknown performance of some of the specimens drove the inclusion of safety features in the flow resistance apparatus to contain specimens that shed particles or fail catastrophically during the testing process. A three-way solenoid valve was placed in the line leading to the upstream inlet of the high resolution transducer and under direct control of the data acquisition computer protected the pressure sensors and test specimens by venting if the pressure exceeded defined limits. Since rapid pressure spikes could occur for test specimens with high flow resistance, a vacuum-assisted particle scavenger hood was designed that could safely contain particles shed during testing.
The specimen holder designed for use in the flow resistance tube was adapted for use with the impedance tube. Some compromises that could lead to an increase in the observed reflection were made to gain the ability to test specimens that could not be manufactured to the precision necessary to fit simpler, more efficient cylindrical holders.
Separate data acquisition and processing programs were written to allow unprocessed data to be stored so processing programs could be modified and re-run against already collected data if an error was found in the processing code. It also allowed large data sets to be handled without encountering memory limitations and to be processed in more than one program for debugging purposes. Finally, this kept the size of the diagram for the main LabVIEW virtual instrument (VI) to a manageable size.
In the end, four different programs specific to the acquisition and processing of that data were developed to take advantage of the different capabilities of each, as well as allowing checks among them to gain confidence in the test results. Calibration data collection, calibration data processing, experimental data acquisition and experimental data processing processing were handled in separate LabVIEW programs. These were based on ASTM and ISO standards, as well as the technique developed by Song and Bolton [11] .
The lack of standard specimens for calibrating the acoustic equipment posed a challenge to verify correct operation. A test specimen of aircraft fiberglass was tested and compared to results obtained at NASA LaRC. The LaRC and GRC spectra were generally similar; with the LaRC spectra showed slightly higher resistance and reactance than the GRC spectra. Since the flow resistance of the fiberglass was known to be sensitive to compression of the material, some of these differences could be attributed to compression of the fiberglass during shipment. However, the development of a simple, inexpensive calibration material for acoustic testing would greatly aid this type of development.
The equipment described was developed with the intent of rapidly screening newly developed candidate material for acoustic absorption applications. While it was expected to produce accurate results, it was designed with the intent of sending the most promising materials to NASA LaRC for more precise and wider-ranging acoustic performance testing. The compromises made for greater variability in the size and shape of a test specimen are not anticipated to adversely affect the performance of either the flow resistance apparatus or acoustic impedance tube for this purpose.
Acknowledgements
The authors wish to acknowledge Dr. Sai Raj and Dr. Louis Ghosn at the NASA Glenn Research Center for their design of the specimen holder for the flow resistivity apparatus. We also acknowledge the support of the Subsonic Fixed Wing and Subsonic Rotary Wing Projects.
Cite this paper
James ChristopherJohnston,Maria A.Kuczmarski,GarthOlszko, (2015) Development of Instrumentation for the Measurement of the Performance of Acoustic Absorbers. Open Journal of Acoustics,05,172-192. doi: 10.4236/oja.2015.54014
References
- 1. Sampath, A. and Balachandran, B. (1997) Studies on Performance Functions for Interior Noise Control. Smart Materials and Structures, 6, 315-332.
http://dx.doi.org/10.1088/0964-1726/6/3/009 - 2. Smith, S.W. (1997) The Scientist and Engineer’s Guide to Digital Signal Processing. California Technical Publishing, San Diego.
- 3. Strobel, J., Wigley, E. and Evans, N. (2009) BUZZ-Acoustical Engineering Methodologies to Measure Student Engagement. Research in Engineering Education Symposium, Palm Cove, 1-6.
- 4. (2003) ASTM Standard C522-03: Standard Test Method for Airflow Resistance of Acoustical Materials.
- 5. Lanoye, R., Bree, H.-E.D., Lauriks, W. and Vermeir, G. (2004) A Practical Device to Determine the Reflection Coefficient of Acoustic Materials in-Situ Based on a Microflown and Microphone Method. International Conference on Noise and Vibration Engineering, Leuven, 11.
- 6. (2004) ASTM Standard C384-04 (Reapproved 2011): Standard Test Method for Impedance and Absorption of Acoustical Materials by Impedance Tube Method.
- 7. (2012) ASTM Standard E1050-12: Standard Test Method for Impedance and Absorption of Acoustical Materials Using a Tube, Two Microphones, and a Digital Frequency Analysis System.
- 8. (2001) BS EN ISO 10534-2: Acoustics—Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes —Part 2: Transfer-Function Method.
- 9. Brigham, E.O. (1974) The Fast Fourier Transform. Prentice-Hall, Englewood Cliffs.
- 10. Jones, M.G. and Stiede, P.E. (1997) Comparison of Methods for Determining Specific Acoustic Impedance. Journal of the Acoustical Society of America, 101, 2694-2704.
http://dx.doi.org/10.1121/1.418558 - 11. Song, B.H. and Bolton, J.S. (2000) A Transfer-Matrix Approach for Estimating the Characteristic Impedance and Wave Numbers of Limp and Rigid Porous Materials. Journal of the Acoustical Society of America, 107, 1131-1152.
http://dx.doi.org/10.1121/1.428404 - 12. National Instruments LabVIEW: Austin, TX.














