Open Journal of Acoustics
Vol.4 No.2(2014), Article
ID:46533,8
pages
DOI:10.4236/oja.2014.42007
Partial Frequencies and Chladni’s Law in Church Bells
William A. Hibbert1, David B. Sharp1, Shahram Taherzadeh1, Robert Perrin2
1Department of Engineering and Innovation, Open University, Milton Keynes, UK
2Institute of Fundamental Sciences, Massey University, Palmerston North, New Zealand
Email: d.sharp@open.ac.uk
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 April 2014; revised 23 May 2014; accepted 29 May 2014
ABSTRACT
The rim partials of a church bell (those with an antinode at the soundbow) generate the strike pitch or perceived note of the bell. The spacing in frequency of the higher rim partials has an important effect on the tonal quality of the bell. Investigations into the partial frequencies of 2752 bells, both bronze and steel, of a wide variety of dates, founders and sizes, show a simple and unexpected relationship between the frequencies of the rim partials. This relationship explains why attempts to tune the higher rim partials independently have failed. A modified version of Chladni’s law provides insight into the musical relationship of the partials, and predicts the partials of individual bells well, but fails to give a simple model of the spacing between the partials seen in bells with different profiles.
Keywords:Church Bell, Partial Frequencies, Chladni’s Law, Timbre, Virtual Pitch, Strike Pitch

1. Introduction
Church bells have a large number of modes of vibration giving rise to partial frequencies in the radiated sound. However, only a small subset of the modes gives rise to significant amplitude in the radiated sound, and an even smaller subset, the rim inextensional radial (RIR) modes, largely determines the perceived tonal quality of the bell.
Figure 1 shows a section through a bell naming the various areas of the profile. The RIR modes have an antinode at the rim of the bell and are preferentially stimulated by the blow of the clapper. Partial frequencies arising from the RIR modes give rise to one or more virtual pitches in the ear which dominate the tonal effect of the bell. Of the five partials normally tuned by bell founders, three arise from RIR modes. If the higher frequency RIR modes are close together (characteristic of a relatively thick bell) or far apart (characteristic of a relatively thin bell) the tonal quality of the bell suffers, due to shifts in the virtual pitches. Details of experiments confirming these effects are given in [1] .
Figure 2 shows the power spectrum of a typical bell. The partials due to the RIR modes (all bar the lowest of which have a single nodal circle in the waist parallel to the rim) are marked with a parameter m equal to the number of complete nodal meridians. These are nodal lines joining diametrically opposed points on the rim, running over the crown of the bell. Figure 3 gives an exaggerated view of the m = 3 mode (which has 3 complete nodal meridians and six nodal points around the rim).
The lower frequency RIR modes have conventional names, as shown in Table1 The partial classification scheme used in this paper is due to Perrin and is taken from [2] (also reprinted in [9] ). As reported in [1] , the Perrin scheme was compared in detail with that proposed by Lehr in [3] (which is translated and reprinted in [9] ) and in [4] , and also with a recent recording of the bell studied in [2] . Very good correspondence was found between the two schemes and the recording.

Figure 1. Section through bell.
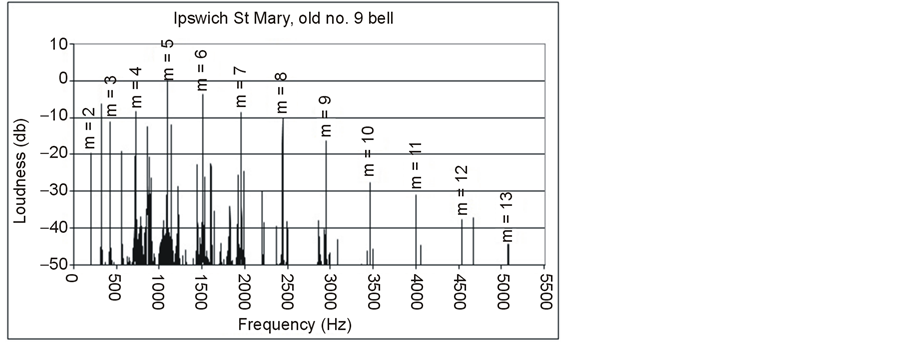
Figure 2. Power spectrum of typical bell.
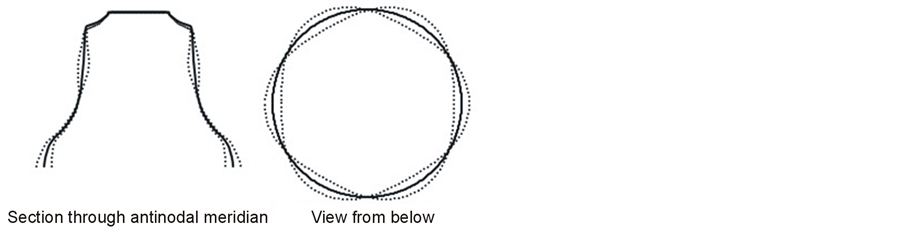
Figure 3. Vibration patterns for m = 3 RIR mode.
The dominant pitch sensation of a bell, commonly termed the strike pitch, is a virtual pitch sensation generated in the human auditory system by a set of partials with an approximate harmonic relationship. The strike pitch of a bell is roughly an octave below the RIR partial m = 4 (the nominal) provided that the nominal lies broadly in the range 500 Hz to 1500 Hz. The m = 4, m = 5, m = 6 and higher RIR partials have frequencies which are approximately harmonically related giving rise to the virtual pitch. If the nominal is lower than 500 Hz, for some listeners a secondary strike note is heard based on the m = 7, m = 9 and m = 11 partials which also have approximately harmonically related frequencies. It is conventional for the named pitch of the bell to be that corresponding to the frequency of the nominal, as it is this partial that plays a major role in determining the strike pitch in most bells. Unlike most other partials, the RIR partials can be reliably identified from recordings because of their prominence and roughly equal spacing.
The work reported in this paper investigates in detail the frequency relationships between the RIR partials, given their importance to the overall tonal effect of church bells.
2. Chladni’s Law Applied to Church Bells
The relationship between the modal frequency and the numbers of nodal lines and nodal circles originally proposed by Chladni for the vibration of flat circular plates, can be generalized and applied to church bells [5] -[8] . The equation developed in [6] and [8] which gave a good fit to the partial frequencies of a single Taylor bell is
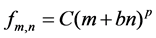 (1)
(1)
where fm,n is the frequency of the mode with m complete nodal meridians and n nodal circles, and C, b and p are constants. The work reported in [6] and [7] was based on the partial frequencies of this single Taylor bell, analysed in detail in [2] . Different values of the constants were needed to ensure a good fit with experimentally measured frequencies for different groups of modes.
For all RIR partials except the hum, n = 1 so Equation (1) simplifies to
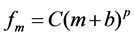 (2)
(2)
The nominal partial is conventionally taken to define the named pitch of the bell. To generalise Equation (2) for bells of different nominal frequencies, it is advantageous to follow custom and quantify the interval of each partial to the nominal as the logarithm of the frequency ratios. If cm is the interval in cents (hundredths of a semitone) between partial frequency fm and the nominal frequency fnom then
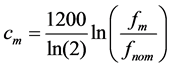 (3)
(3)
where the constant of proportionality arises because there are 1200 cents in an octave.
Writing K = 1200/ln(2) for clarity and expanding the logarithm gives
 (4)
(4)
Finally, substituting (2) into (4) and re-arranging gives
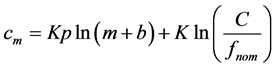 (5)
(5)
Equation (5) suggests that, if the modified Chladni law applies to the RIR partials, plotting cm against ln(m + b) should demonstrate a linear relationship with gradient Kp and intercept K ln(C/fnom) for a suitable value of b. The logarithmic formulation illuminates the use of cents as a way of relating partial frequencies. Equation (5) also expresses musical characteristics of the bell, as the quantity cm is the musical interval between each partial and the nominal (and therefore the strike pitch).
3. Relationship between RIR Partial Frequencies in Bells
The RIR partial frequencies of 2752 bells were obtained from individual recordings by use of a spectrum analysis package. 73% of the recordings were made by one of the authors (WAH). The bells were from 21 different countries, had weights from a few kg to 65 tonnes, casting dates ranging over 7 centuries, hum frequencies from 47.5 Hz to 4702 Hz (i.e. a range of 6 and a half octaves) and were the product of at least 100 different founders. 48 English and German steel bells were included.
RIR partial frequencies for the octave nominal and lower partials were measured for all the bells. RIR partial frequencies above the octave nominal were measured for approximately half the bells (chosen to explore the ranges of weight and RIR partial spacing). Due to limitations of the recording devices, not all of the upper partials could be detected for some of the bells. The total number of times each partial was successfully measured, across the 2752 bells investigated, is given in Table2
The RIR partial frequencies were converted into cents relative to the nominal using Equation (3). Linear correlations were calculated of the resulting intervals in cents for all the possible pairs of partials (e.g. the correlation of all values of m = 2 against m = 3, of m = 2 against m = 4, of m = 2 against m = 5, etc.). The correlations took account of missing values, i.e. those partial frequencies which could not be measured. The results of the linear correlations for pairs of partials are shown in Table3 A correlation of 1 indicates an exact linear relationship; a correlation of −1 indicates an exact negative linear relationship.
It is clear from these results that all the RIR partials from m = 5 upwards are highly positively correlated with one another. There is some correlation with the tierce (m = 3) and hum (m = 2) but much less strong, and in the opposite direction—as the higher partials go sharper relative to the nominal, the tierce and hum tend to go flatter. Scatter diagrams of the individual partials against one another confirm the linear relationship. Figure 4 shows the relationship between the superquint (m = 5) and octave nominal (m = 6). Both bronze and steel bells show the same linear relationship. The outliers, with high values for the interval between octave nominal and nominal, are all very thin, unpleasant sounding bells.
Work reported in [1] shows that there is an inverse correlation between the relative weight of bells and the upper partial spacing. Bells which are heavier than the average for a given nominal have flatter upper partials, and vice versa. This is confirmed by measurements on bells before and after tuning, showing that the tuning process tends to sharpen all the upper partials.
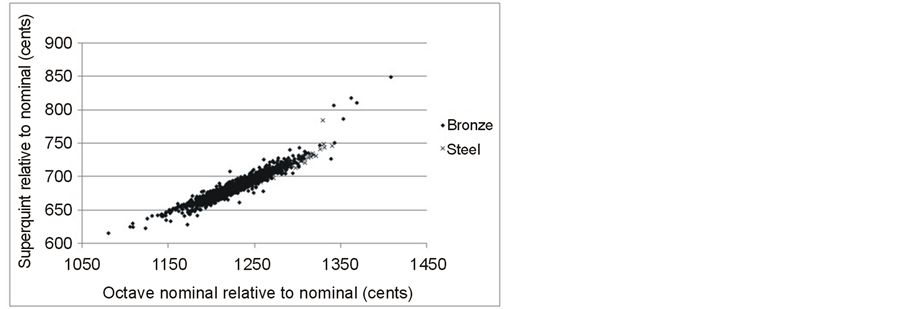
Figure 4. Superquint relative to nominal (in cents) plotted against octave nominal relative to nominal (in cents).
The scatter plot in Figure 5 for all the RIR partials up to m = 11 confirms the linear relationships. Figure 5 shows that, for all the RIR partials above the nominal, there is a strong linear relationship between their tuning in cents relative to the nominal, such that if the tuning of any one of these partials is given, the frequencies of all are determined. The importance of this conclusion to bell founding is that it is not possible, in a bell of conventional western design, to independently influence the tuning of the upper RIR partials either by design or work on the tuning machine, despite bell founders’ attempts to the contrary. As can be seen from the plot, this is also generally true for the tierce (m = 3). Bell founders do not attempt to move the tierce relative to the nominal on the tuning machine, relying on changes in the shape of the rim when moulding the bell to control this partial.
For the hum (m = 2), it is clear from the wider scattering of points around the m = 2 line on Figure 5, that changes independent of the upper RIR partials are possible. The hum, despite being an RIR partial, is unique in having no nodal circle parallel to the rim, so that changes in the profile of the bell can affect this partial differently to the remaining RIR partials. The horizontal set of values at −2400 cents for the hum, and at −900 cents for the tierce, represents true-harmonic bells, about 36.5% of the total.
The octave nominal (m = 6) was chosen as a parameter for all the upper partials, because practical experience shows it can always be measured in all but the smallest bells, and its correlation with the other upper RIR partials is strong. Regression fits of the intervals in cents of all RIR partials (relative to the nominal) against the interval in cents of the octave nominal (relative to the nominal) give rise to the results in Table4 Also, 95% confidence intervals are provided.
The final two columns in Table 4 give the standard deviation (SD) of the residuals of the model values against the actual values, both as an absolute figure and as a percentage of the average value. The small residuals for the partials above the nominal confirm that the interval in cents of the octave nominal relative to the nominal can be used very effectively to represent the tuning of all the upper RIR partials and hence their effect on the musical quality of the bell. The intercept of all the upper RIR partials apart from m = 11 is less than the confidence limit, so that the regression lines can be regarded as passing through the origin. As will be seen below, this model can be used to predict well the frequencies of all the upper partials of a bell, once the frequencies of nominal (m = 4) and octave nominal (m = 6) are known.
In the remainder of this paper, this linear relationship between the interval in cents of each of the upper partials (relative to the nominal) and the interval in cents of the octave nominal (relative to the nominal) is referred to as the linear model.
4. Fit of Bell Partials to the Chladni Model
The previous section showed how expressing the frequencies of the RIR partials in terms of cents relative to the nominal frequency indicated a simple linear relationship between them all. This section explores the extent to which this linear relationship is predicted by the modified Chladni model as expressed in Equation (5). Because this equation is non-linear in quantity b, it is necessary to use an iterative approach to obtain the best fit. A classic linear regression provided the best fit values for Kp (the slope) and K ln(C/fnom) (the intercept). Using K = 1200/ln(2) ≈ 1731.234 allows the parameter p in the original model of Equation (1) to be calculated.
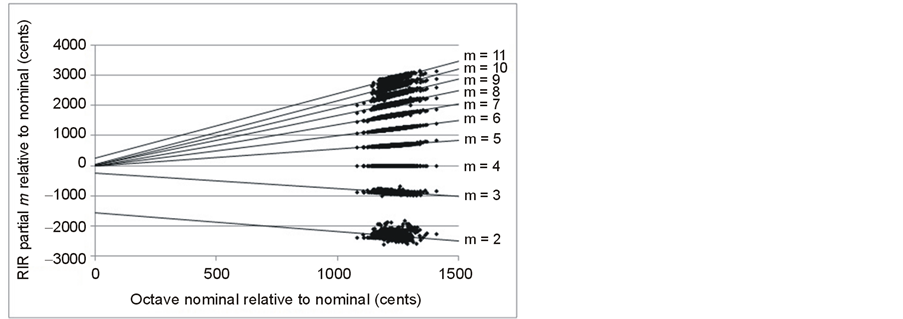
Figure 5. RIR partials relative to nominal (in cents) plotted against octave nominal relative to nominal (in cents).
Table 4. Regression of intervals in cents of all partials (relative to nominal) against interval in cents of octave nominal (relative to nominal).
It was found that different values of p and b were needed to give best fits to the partials of different bells. To show the range of values, five different cases were investigated:
• the old no. 1 bell from Kidderminster in Worcestershire (a bell with very flat upper partials)
• no. 7 bell from Warnham in Sussex (a bell with moderately flat upper partials)
• the average of all 2752 bells
• no. 2 bell from Tealby in Lincolnshire (a bell with moderately sharp upper partials)
• no. 9 bell from the chime at Rostov in Russia (a bell with very sharp upper partials).
The form of Equation (1) suggests that for the hum partial, which has no nodal circle in the waist (i.e. n = 0), ln(m) rather than ln(m + b) is the appropriate independent variable. However, as discussed in [7] , setting n = 1 rather than n = 0 for the hum gives a much better fit, and this approach was adopted in the analysis.
A plot of the intervals in cents of the partials relative to the nominal for each of the 2752 bells against ln(m + b), using for b the best fit for the average of all bells, appears as Figure 6 and shows the anticipated linear relationship. The lines are the best fit regressions for the two extreme cases (the Kidderminster no.1 bell and the Rostov no.9 bell) and for the average. There is clearly a considerable difference in slope and intercept for these three cases. The results of the iterative fit and regression for the five different cases under investigation are shown in Table5
Due to the wide range in values for p, b and C required for different bells, the fact that the parameters do not change monotonically with the octave nominal, and the non-linear nature of the relationship, there is no simple parameter to express changes in bell profile as is provided by the octave nominal for the linear model.
The Chladni model using the above parameters provides a good fit to the actual measured partials of the bells as shown in Table6 The SD of all residuals for these five cases is 16.48; the SD of residuals for all the bells in the linear model is 40.78. It should be pointed out that parameters for each bell are individually fitted for the Chladni model; the linear model has a single set of parameters for all bells.
Table 6 shows predicted model values and actual measurements for the four bells investigated and for the average of all 2752 bells. (The nominal and octave nominal are exact in the linear model because of the way the model is constructed.) The fit of the Chladni model is noticeably better than the linear model for the hum and tierce in most bells but does predict a nominal up to 25 cents or 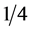 of a semitone out. Apart from this, the two models are comparable.
of a semitone out. Apart from this, the two models are comparable.
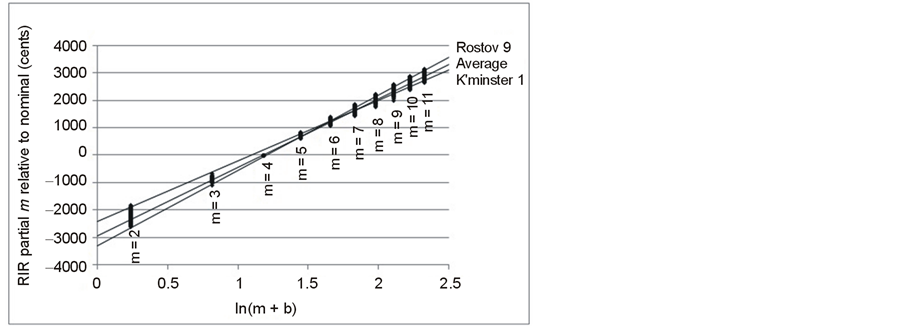
Figure 6. Chladni model for RIR partials of 2752 bells.
Table 6. Model predictions for partial intervals relative to nominal (in cents) for four individual bells and for average of all 2752 bells.
5. Conclusions
The analysis of these 2752 bells has shown that the modified Chladni model as proposed by Rossing and Perrin provides a new insight into the relative tuning of the RIR partials of bells of Western shape. The use of cents relative to the nominal partial as a way of expressing the frequencies of these partials, suggested by the model, turns out to show an unexpected relationship between all the upper RIR partials. This relationship shows why attempts by bell founders to tune these upper partials independently have not been successful.
The analysis also shows that the wide variation in intervals between the upper partials in bells of different profiles can be represented by a single parameter—the interval between the octave nominal and nominal. This allows the effect of the upper RIR partials on the pitch and timbre of bells to be represented by this single quantity.
The modified Chladni model proves to be a good fit to the four sample bells and the average of all bells. This is remarkable given the considerable difference in shape and vibrational characteristics of bells from flat plates, where the model was first proposed. This in turn may help theoretical insights into the relation between the RIR partials in bells.
However, the Chladni model has an awkward form, involving three parameters in a non-linear relationship, which have to be individually fitted for each bell, and which do not have an obvious correlation to the octave nominal and hence the tonal quality and shape of the bell. This means that the practical application of the Chladni model to bell partial analysis and bell tuning is not straightforward.
References
- Hibbert, W.A. (2008) The Quantification of Strike Pitch and Pitch Shifts in Church Bells. Ph.D. Thesis, The Open University, UK.
- Perrin, R., Charnley, T. and DePont, J. (1983) Normal Modes of the Modern English Church Bell. Journal of Sound and Vibration, 90, 29-49. (Reprinted in [9]) http://dx.doi.org/10.1016/0022-460X(83)90401-7
- Lehr, A. (1965) Contemporary Dutch Bell-Founding Art; Hedendaagse Nederlandse Klokkengietkunst. Netherlands Acoustical Society Publication, 7, 20-40. (Translated and reprinted in [9])
- Lehr, A. (1986) Partial Groups in the Bell Sound. Journal of the Acoustical Society of America, 79, 2000-2011. http://dx.doi.org/10.1121/1.393208
- Fletcher, N.H. and Rossing, T.D. (1998) The Physics of Musical Instruments. 2nd Edition, Springer.
- Perrin, R., Charnley, T., Banu, H. and Rossing, T.D. (1985) Chladni’s Law and the Modern English Church Bell. Journal of Sound and Vibration, 102, 11-19. http://dx.doi.org/10.1016/S0022-460X(85)80100-0
- Perrin, R. and Charnley, T. (1987) On the RIR Modes of the Modern English Church Bell. Journal of Sound and Vibration, 119, 243-247. http://dx.doi.org/10.1016/0022-460X(87)90452-4
- Rossing, T.D. and Perrin, R. (1987) Vibrations of Bells. Applied Acoustics, 20, 41-70. http://dx.doi.org/10.1016/0003-682X(87)90082-X
- Rossing, T.D. (Ed.) (1984) Acoustics of Bells. Van Nostrand Reinhold.


