Open Journal of Acoustics
Vol.4 No.1(2014), Article ID:44032,6 pages DOI:10.4236/oja.2014.41003
On the Existence of Subharmonic Screech in Choked Circular Jets from a Sharp-Edged Orifice
Max Kandula
ESC-Team QNA, NASA Kennedy Space Center, USA
Email: max.kandula-1@nasa.gov
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 15 February 2014; revised 15 March 2014; accepted 20 March 2014
ABSTRACT
Experiments are performed in choked circular hot and cold nitrogen jets issuing from a 2.44 cm diameter sharp-edged orifice at a fully expanded jet Mach number of 1.85 in an effort to investigate the character of screech phenomenon. The stagnation temperature of the cold and the hot jets are 299 K and 319 K respectively. The axial distribution of the centerline Mach number was obtained with a pitot tube, while the screech data (frequency and amplitude) at different axial and radial stations were measured with the aid of microphones. The fundamental screech frequency of the hot jet is slightly increased relative to that of the cold jet. It is concluded that temperature effects on the screech amplitude are manifested with regard to the fundamental and the subharmonic even at relatively small temperature range considered.
Keywords:Subharmonic Screech; Sharp-Edged Orifice; Circular Jets; Thermal Effects

1. Introduction
Supersonic jet screech represents an important concern as the intensity (as high as 170 to 180 dB) in the nearfield with a significant upstream directivity can induce fatigue and cause structural damage to aircraft and launch vehicles [1] -[3] . The fundamental physics of screech was uncovered by Powell [4] [5] , who identified the mechanism of supersonic jet screech in terms of a resonant feedback loop. Several others followed it up with more details. For a detailed review of jet screech, see Raman [6] .
It is generally believed that the screech tones are generated by the interaction between instability waves (vortices) developed from the nozzle lip area and the shock-cell structures [2] . It was recently shown [7] that screech noise amplification is manifested by the interaction of shock-cell structures with acoustics waves. The existing data on the screech noise, which are primarily limited to convergent-divergent and choked nozzles, suggest that uncertainties persist concerning the nature of the temperature effects on the fundamental and higher harmonics [8] .
To the author’s knowledge, screech data from choked jets issuing from a sharp-edged orifice are relatively scarce. Such important practical applications typically arise in purge systems, where the screech from the purged jet can induce fatigue on neighboring electro-mechanical components. Some of the experimental works reported on the tonal noise from orifices are those of Anderson [9] , Chanaud and Powell [10] and Succi [11] . In a somewhat related work, Ingard and Singhal [12] investigated the resonance of an open-ended duct. The majority of studies were concerned with screech frequency, and screech amplitude appears to be considered only by Succi [11] , but this is only for a parallel orifice plate configuration.
The objectives of the present work are to report preliminary measurements of screech frequency and amplitude for a cold jet (stagnation temperature less than or equal to the ambient temperature) and a hot jet (stagnation temperature exceeding the ambient temperature) issuing from a sharp-edge orifice at the same fully expanded jet Mach number, and to characterize the screech behaviour with regard to convergent-divergent nozzles. This work is based on the author’s recent presentation [13] , where preliminary interpretations of screech data for nitrogen jets from a sharp-edged orifice are recorded.
2. Experimental Setup
A schematic of the configuration is presented in Figure 1. Nitrogen flows from a long aluminium tube of 3.81 cm diameter through a sharp-edged orifice of 2.44 cm diameter. Table 1 identifies the flow parameters.
The total pressure  is 0.65 MPa. The total temperature
is 0.65 MPa. The total temperature 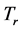 for the hot jet and the cold jet are 319.4 K and 299 K respectively. The jet static pressure ratio (jet exist pressure to ambient pressure) is 3.18, and the ambient temperature
for the hot jet and the cold jet are 319.4 K and 299 K respectively. The jet static pressure ratio (jet exist pressure to ambient pressure) is 3.18, and the ambient temperature  is 299 K. The fully expanded jet Mach number is 1.85. The jet exit Mach number
is 299 K. The fully expanded jet Mach number is 1.85. The jet exit Mach number  is 1.05. The jet Reynolds number (based on jet diameter) is about 2.5 × 106. Static pressure and total pressure are measured by pitot tubes, and the acoustic pressure is measured by B&K Model 4189 microphones with a frequency range of 6.3 to 20 kHz. Both axial and radial traversing in the jet is carried out. The three microphone locations are denoted by L1, L2, and L3. The local Mach number can be calculated using Rayleigh’s pitot tube formula [14] .
is 1.05. The jet Reynolds number (based on jet diameter) is about 2.5 × 106. Static pressure and total pressure are measured by pitot tubes, and the acoustic pressure is measured by B&K Model 4189 microphones with a frequency range of 6.3 to 20 kHz. Both axial and radial traversing in the jet is carried out. The three microphone locations are denoted by L1, L2, and L3. The local Mach number can be calculated using Rayleigh’s pitot tube formula [14] .
3. Results
3.1. Jet Flowfield
Figure 2 displays the variation of the measured jet centre-line Mach number for the hot jet. The center-line Mach number displays the characteristic oscillations of the underexpanded jet on account of the presence of the shock cell structures. Mach number oscillations seem to be absent beyond about 10 jet diameters. The maximum measured center-line Mach number is about 1.78 occurring near the first shock cell, and is comparable to the theoretical fully expanded jet Mach number of 1.85.
It is evident from the Mach number oscillations that the shock cell spacing is nearly uniform. From the data of Harper-Bourne and Fisher [15] , the shock-cell spacing 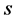 may be taken as roughly uniform and given by
may be taken as roughly uniform and given by
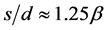 (1a)
(1a)
where  is the orifice diameter, the pressure ratio parameter
is the orifice diameter, the pressure ratio parameter 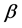 is defined by
is defined by

Figure 1. Schematic of the experimental configuration and microphone setup.
Table 1. Test conditions.
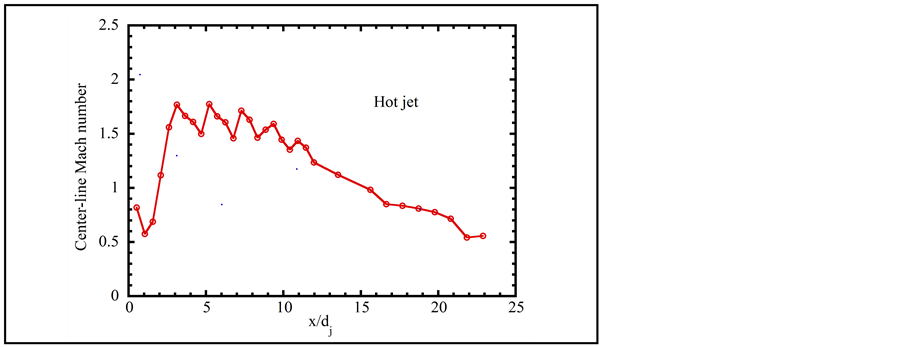
Figure 2. Distribution of jet center-line Mach number for the hot jet.
 (1b)
(1b)
where 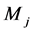 refers to the fully expanded jet Mach number. Equation (1) thus suggests a value of
refers to the fully expanded jet Mach number. Equation (1) thus suggests a value of  or
or 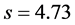 cm. The measured shock-cell spacing is in close agreement with the data of Harper-Bourne and Fisher [15] . It is generally known that the strongest interaction usually occurs at the third through the fifth shock cell [7] , the highest pressure amplification occurring at the first shock cell.
cm. The measured shock-cell spacing is in close agreement with the data of Harper-Bourne and Fisher [15] . It is generally known that the strongest interaction usually occurs at the third through the fifth shock cell [7] , the highest pressure amplification occurring at the first shock cell.
The pressure data and infrared photographs suggest a jet spread of about 7 deg. The reduced jet shear layer growth compared with the incompressible case (12 degrees nominal) is primarily due to the effects of compressibility (Mach number effect) [16] -[18] . It is known that the shear layer growth rate decreases with Mach number and increases with jet temperature. Preliminary calculations show that at a fully expanded jet Mach number (1.85 in the present case) the jet growth rate is about 60% of that for the incompressible case.
3.2. Narrowband Acoustic Spectra
Figure 3 illustrates the narrow band spectral sound pressure level (SPL) for the hot and the cold jet at an axial station of 48.3 cm from the jet exit, and at two radial locations (17.8 cm and 45.7 cm). These locations correspond to microphones L1 and L2 respectively. Figure 4 indicates the narrow band spectral sound pressure level for the hot and the cold jet at an axial station of 78.7 cm from the jet exit, and at a radial location of 40.6 cm (microphone L3). These data for the free jets reveal the presence of screech, and include the overall sound pressure level (OASPL).
As noticed from Figure 3, the OASPL is found to be 133 dB and 126 dB respectively for stations L1 and L2 respectively. The narrow band spectra for the cold and the hot jets at both these locations are close to each other, thus leading to OASPL that are nearly the same for both the cold and the hot jets.
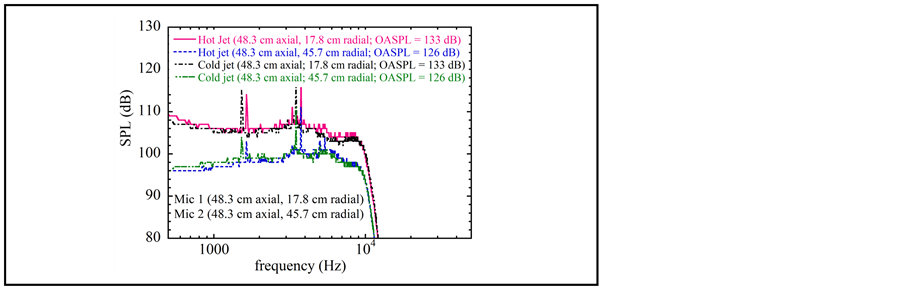
Figure 3. Narrowband acoustic spectrum for cold and hot jets for microphones 1 and 2.
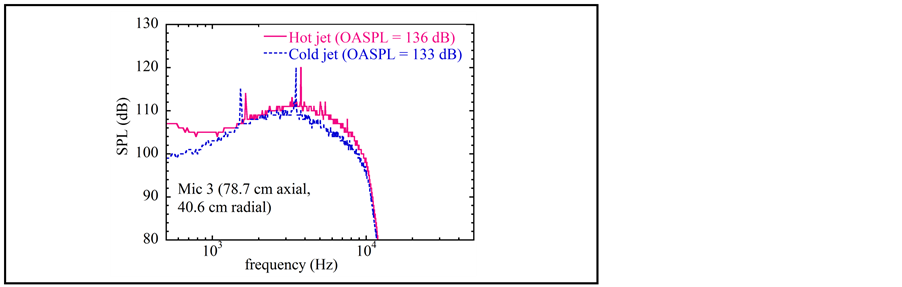
Figure 4. Narrowband acoustic spectrum for cold and hot jets for microphone 3.
Referring to Figure 4, the OASPL at station L3 is found to be 136 dB and 133 dB for the hot jet and the cold jet respectively. This deviation in OASPL is evident from the difference in the narrowband spectrum for the cold and the hot jet, particularly at low and high frequencies.
The narrowband spectra for the cold and the hot jets reveal the existence of a fundamental screech as well as a strong subharmonic screech.
Table 2 presents a summary of the measured screech frequencies 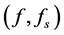 and amplitudes (SPL) of the subharmonic and the fundamental tones for both the cold and the hot jets at the three microphone locations. The subscript s refers to the subharmonic. The measurements suggest that the fundamental screech amplitude and frequency for the hot jet are slightly increased relative to the cold jet. With regard to the subharmonic, the hot jet is generally characterized by decreased screech amplitude and an increased frequency compared with the cold jet.
and amplitudes (SPL) of the subharmonic and the fundamental tones for both the cold and the hot jets at the three microphone locations. The subscript s refers to the subharmonic. The measurements suggest that the fundamental screech amplitude and frequency for the hot jet are slightly increased relative to the cold jet. With regard to the subharmonic, the hot jet is generally characterized by decreased screech amplitude and an increased frequency compared with the cold jet.
3.3. Screech Frequency
Predictions are made for the fundamental screech frequency  based on the following well-known correlation proposed by Tam et al. for convergent and convergent-divergent nozzles [19] :
based on the following well-known correlation proposed by Tam et al. for convergent and convergent-divergent nozzles [19] :
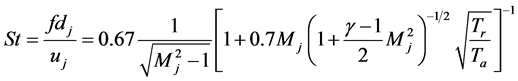 (2a)
(2a)
In the preceding equation, 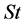 is the Strouhal number,
is the Strouhal number, 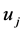 is the fully expanded jet velocity,
is the fully expanded jet velocity,  is the fully expanded jet Mach number (1.85 in our present case),
is the fully expanded jet Mach number (1.85 in our present case), 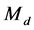 is the design (exit) Mach number (1.05 in our present case),
is the design (exit) Mach number (1.05 in our present case),  the reservoir temperature,
the reservoir temperature, 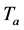 the ambient temperature,
the ambient temperature,  the isentropic exponent (specific heat ratio), and
the isentropic exponent (specific heat ratio), and 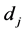 the effective jet diameter (or the fully expanded jet diameter). The effective (fully expanded) jet diameter is evaluated from the relation [19] :
the effective jet diameter (or the fully expanded jet diameter). The effective (fully expanded) jet diameter is evaluated from the relation [19] :
Table 2. Summary of the screech frequencies and excess screech amplitudes.
 (2b)
(2b)
where  is the jet exit diameter. The preceding expression for the screech frequency is in excellent agreement with experimental data for convergent and convergent-divergent nozzles over a wide range of fully expanded jet Mach numbers. Equation (2) suggests that the screech frequency is not strongly dependent on the jet temperature.
is the jet exit diameter. The preceding expression for the screech frequency is in excellent agreement with experimental data for convergent and convergent-divergent nozzles over a wide range of fully expanded jet Mach numbers. Equation (2) suggests that the screech frequency is not strongly dependent on the jet temperature.
The predicted screech frequency of the fundamental from the foregoing correlation is found to be 3.62 kHz for the cold jet , which is compared with the measured value of 3.5 kHz (Table 2). The corresponding predicted fundamental screech frequency for the hot jet
, which is compared with the measured value of 3.5 kHz (Table 2). The corresponding predicted fundamental screech frequency for the hot jet 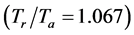 is found to be 3.69 kHz, which compares with the measured value of 3.77 kHz. The measured and predicted fundamental screech frequencies for the hot jet are seen to slightly exceed those for the cold jet.
is found to be 3.69 kHz, which compares with the measured value of 3.77 kHz. The measured and predicted fundamental screech frequencies for the hot jet are seen to slightly exceed those for the cold jet.
The results suggest the existence of subharmonic screech in both the cold and the hot jets with a frequency of about 1.6 kHz. Such subharmonic screech tones have been well-known in jets discharging from axisymmetric nozzles both from numerical and experimental work [20] -[22] . Subharmonics were also recently predicted by Tolstykh and Shirobokov [23] , who considered 2-D jet screech with the aid of a highly accurate multi-operators-based compact differencing scheme.
The fundamental mechanism for the generation of subharmonic screech in convergent-divergent is generally known to be due to the formation of (axisymmetric) vortex pairing at the nozzle exit [22] -[24] , which is believed to be responsible for the subharmonic screech for the jet issuing from a sharp-edged orifice.
3.4. Screech Amplitude
The measured amplitudes suggest the existence of relatively strong subharmonics. The subharmonic screech amplitude is of comparable magnitude in relation to the fundamental, and thus it is important to characterize the subharmonic and take it into account concerning the system design. To the author’s knowledge, screech data for the subharmonic amplitude and its directivity is presently lacking in the literature insofar as jets issuing from sharp-edged orifices are concerned. The subharmonics also appear to possess upstream directivity, see Loh and Hultgren [22] .
4. Conclusion
The present experiments on choked circular jets emanating from a sharp-edged orifice reveal the existence of screech subharmonic tones along with the fundamental for both the cold and the hot jets, with no higher harmonics present. The existing formulation for screech frequency proposed for convergent or convergent/divergent nozzles satisfactorily applies to jets issuing from sharp-edged orifices. The fundamental screech frequency of the hot jet is slightly increased relative to that of the cold jet. Considering the relatively narrow temperature range considered here, it is concluded that the screech amplitudes for the fundamental and the subharmonic for the hot jet deviate from those of the cold jet.
Acknowledgements
The author thanks Geoffrey Rowe of ESC-Team QNA with regard to data acquisition. Thanks are also due to Stanley Starr (Chief, Applied Physics Branch) of NASA Kennedy Space Center for review and helpful suggestions. The author is grateful to the reviewers for helpful comments and suggestions.
References
- Kandula, M. (2009) Broadband Shock Noise Reduction in Turbulent Jets by Water Injection. Applied Acoustics, 70, 1009-1014. http://dx.doi.org/10.1016/j.apacoust.2008.12.001
- Kandula, M. (2008) On the Scaling Laws and Similarity Spectra for Jet Noise in Subsonic and Supersonic Flow. International Journal of Acoustics and Vibration, 16, 3-16.
- Kandula, M. (2008) Nearfield Acoustics of Clustered Rocket Engines. Journal of Sound and Vibration, 309, 852-857. http://dx.doi.org/10.1016/j.jsv.2007.06.078
- Powell, A. (1953) On the Mechanism of Choked Jet Noise. Proceeding of the Physical Society of London B, 66, 1039-1056.
- Powell, A. (1953) The Noise of Choked Jets. Journal of the Acoustical Society of America, 25, 385-389. http://dx.doi.org/10.1121/1.1907052
- Raman, G. (1999) Supersonic Jet Screech: Half-Century from Powell to the Present. Journal of Sound and Vibration, 225, 543-571. http://dx.doi.org/10.1006/jsvi.1999.2181
- Kandula, M. (2008) Shock-Refracted Acoustic-Wave Model for Screech Amplitude in Supersonic Jets. AIAA Journal, 40, 682-689. http://dx.doi.org/10.2514/1.30913
- Krothapalli, A., Soderman, P.T., Allen, C.S., Hayes, J.A. and Jaeger, S.M. (2007) Flight Effects on the Far-Field Noise of a Heated Supersonic Jet. AIAA Journal, 35, 952-957. http://dx.doi.org/10.2514/2.203
- Anderson, A.B.C. (1954) A Jet-Tone Orifice Number for Orifices of Small Thickness-Diameter Ratio. Journal of the Acoustical Society of America, 25, 21-25. http://dx.doi.org/10.1121/1.1907284
- Chanaud, R.C. and Powell, A. (1965) Some Experiments Concerning the Hole and Ring Tones. Journal of the Acoustical Society of America, 37, 902-911.
- Succi, G.P. (1986) Flow-Generated Noise in Circular Cavities or How Teapots Whistle. Noise Control Engineering Journal, 26, 8-16. http://dx.doi.org/10.3397/1.2827657
- Ingard, K.U. and Singhal, V.K. (1975) Effect of Flow on the Acoustic Resonance of an Open-Ended Duct. Journal of the Acoustical Society of America, 58, 778-779. http://dx.doi.org/10.1121/1.380751
- Kandula, M. (2012) Measurements of Thermal Effects on Acoustic Screech in a Choked Circular Jet Emanating from a Sharp-Edged Orifice. Proceedings of the 23rd International Congress on Theoretical and Applied Mechanics, Beijing, 19-24 August 2012.
- Shapiro, A. (1953) The Dynamics and Thermodynamics of Compressible Fluid Flow. McGraw-Hill, New York.
- Harper-Bourne, M. and Fisher, M.J. (1973) The Noise from Shock Waves in Supersonic Jets. Proceedings of the AGARD Conference on Noise Mechanisms, AGARD CP-131, 11-1 to 11-13.
- Gloebel, S.G. and Dutton, J.C. (1991) Experimental Study of Compressible Turbulent Mixing Layers. AIAA Journal, 29, 453-477.
- Schlichting, H. (1979) Boundary Layer Theory. 7th Edition, McGraw-Hill, New York.
- Kandula, M. and Wilcox, D.C. (1995) An Examination of
 Turbulence Model for Boundary Layers, Free Shear Layers and Separated Flows. AIAA Paper 1995-2317.
Turbulence Model for Boundary Layers, Free Shear Layers and Separated Flows. AIAA Paper 1995-2317. - Tam, C.K.W., Seiner, J. and Wu, J.C. (1986) Proposed Relationship between Shock and Screech Tones. Journal of Sound and Vibration, 81, 337-358. http://dx.doi.org/10.1016/0022-460X(82)90244-9
- Walker, S.H. and Thomas, F.O. (1997) Experiments Characterizing Nonlinear Shear Layer Dynamics in a Supersonic Rectangular Jet. Physics of Fluids, 9, 256. http://dx.doi.org/10.1063/1.869373
- Berland, J., Bogey, C. and Bailly, C. (2007) Numerical Study of Screech Generation in a Planar Supersonic Jet. Physics of Fluids, 19, 105-114.
- Loh, C.Y. and Hultgren, L.S. (2006) Jet Screech Noise Computation. AIAA Journal, 44, 992-998. http://dx.doi.org/10.2514/1.4591
- Tolstykh, A.I. and Shirobokov, D.A. (2013) Fast Calculations of Screech Using Highly Accurate Multiprocessor-Based Schemes. Applied Acoustics, 74, 102-109. http://dx.doi.org/10.1016/j.apacoust.2012.06.013
- Samimy, M., Kim, J.-H., Kearney-Fischer, M. and Sinha, A. (2010) Acoustic and Flow Fields of an Excited High Reynolds Number Axisymmetric Supersonic Jet. Journal of Fluid Mechanics, 656, 507-529.


