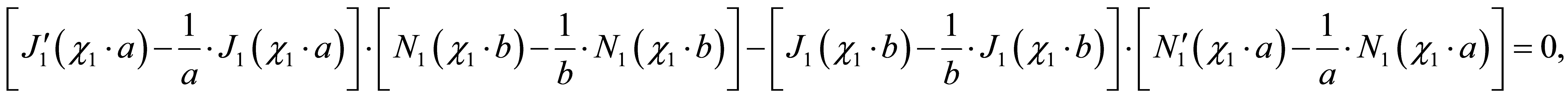Open Journal of Acoustics
Vol.3 No.3(2013), Article ID:36740,5 pages DOI:10.4236/oja.2013.33011
Against Phase Veloсities of Elastic Waves in Thin Transversely Isotropic Cylindrical Shell
St. Prtersburg State Marine Technical University, St. Petersburg, Russia
Email: alexalex-2@yandex.ru
Copyright © 2013 Alexander Kleshchev. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 18, 2013; revised August 18, 2013; accepted August 25, 2013
Keywords: theory of elasticity; phase velocity; transversely isotropic medium; characteristic equation
ABSTRACT
This paper receives the characteristic equation for the determine of wave numbers of phase velocities of elastic waves, in the thin cylindrical shell with the help of the dynamic theory of the elasticity for the transversely isotropic medium and of the hypothesis of thin shells.
1. Introduction
Based on the use of the dynamic theory of the elasticity for the anisotropic medium and with the help of the hypothesis of thin shells, this paper is determined by the characteristic equation for wave numbers of elastic waves in the thin transversely isotropic cylindrical shell.
2. The Dynamic Theory of the Elasticity for the Transversely Isotropic Medium
Let’s consider the infinite thin transversely isotropic cylindrical shell. The elastic wave is spread along the axis  that orthogonal of the plane of the isotropy. The transversely isotropic elastic medium is characterized by five elastic moduluses [1]:
that orthogonal of the plane of the isotropy. The transversely isotropic elastic medium is characterized by five elastic moduluses [1]:  or by technical moduluses
or by technical moduluses 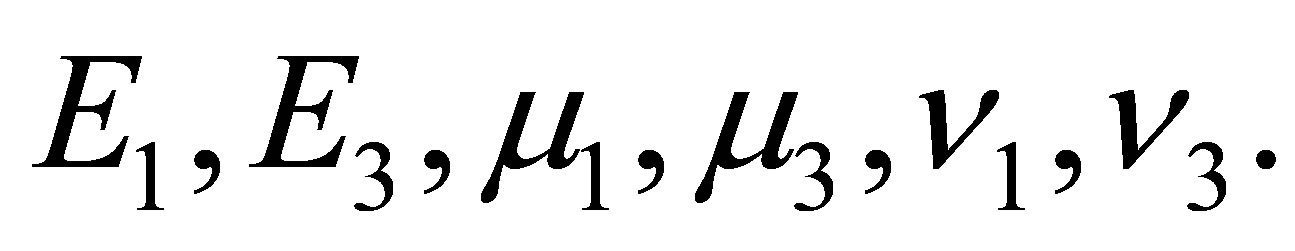 In the chosen orientation of the axis
In the chosen orientation of the axis  is the Joung’s modulus,
is the Joung’s modulus, 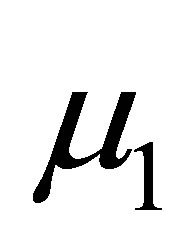 is the shear modulus,
is the shear modulus, 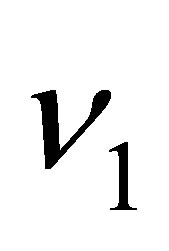 is the Poisson’s ratio in the plane of the isotropy.
is the Poisson’s ratio in the plane of the isotropy. 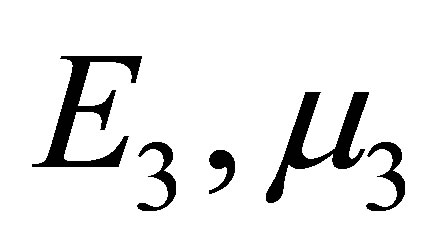 and
and  are the same values in the transverse plane. These moduluses connected with each other by the relationship [1-4]:
are the same values in the transverse plane. These moduluses connected with each other by the relationship [1-4]:
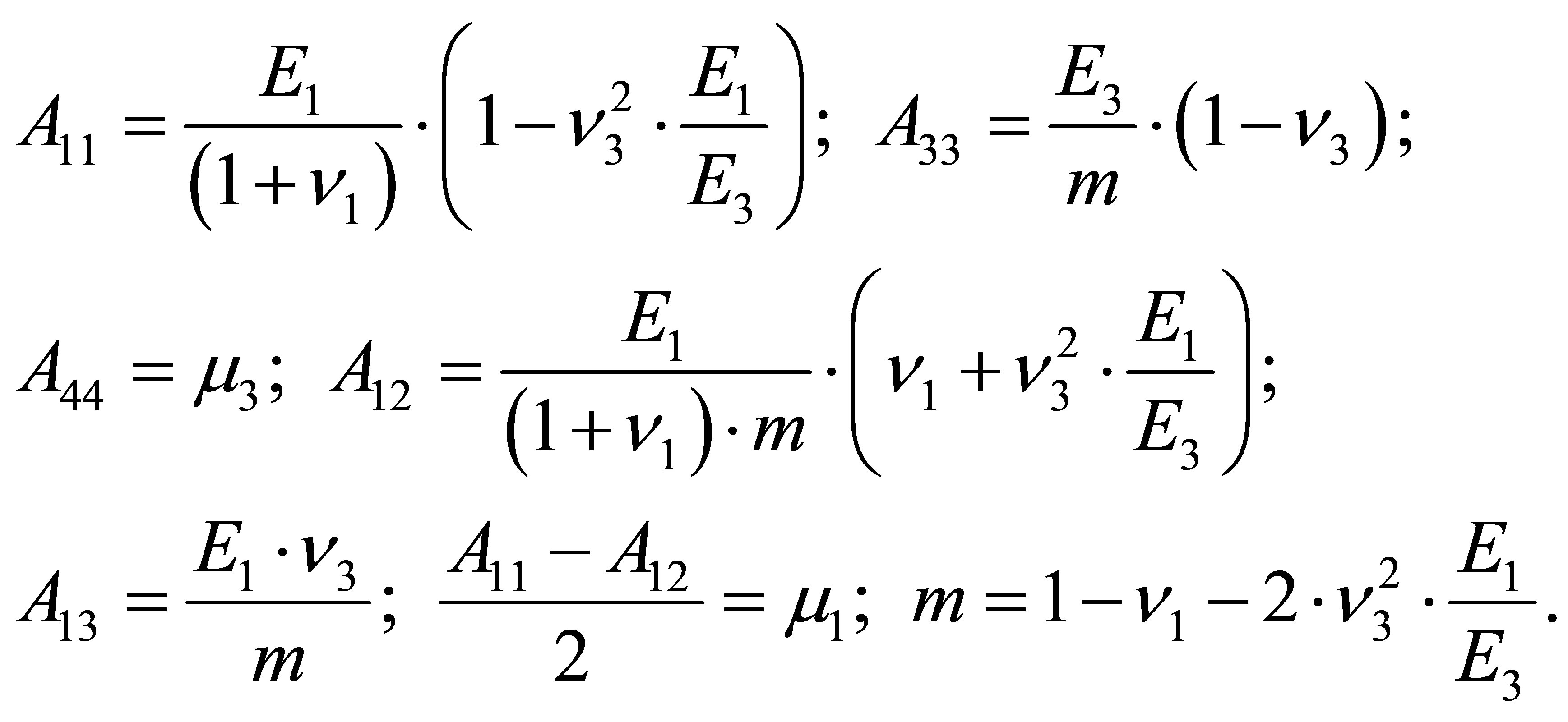 (1)
(1)
The Hooke’s law for the transversely isotropic elastic medium is written in the next form [1]:
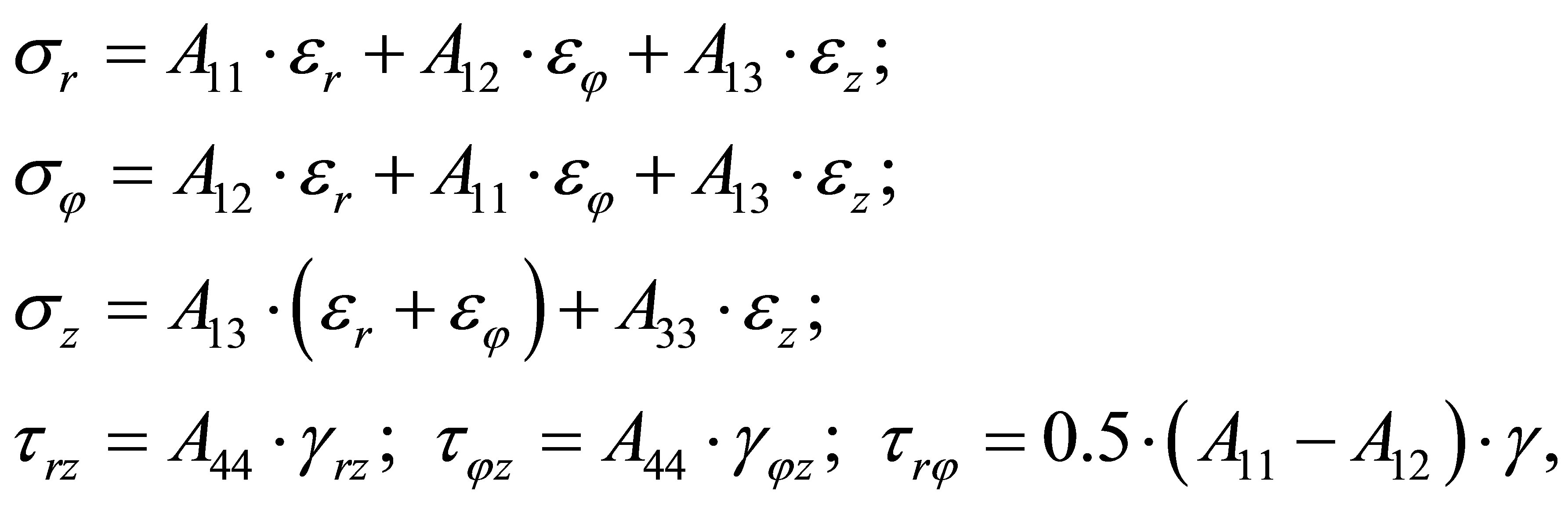 (2)
(2)
where  are components of the tensor of deformations, which are equals [1]:
are components of the tensor of deformations, which are equals [1]:
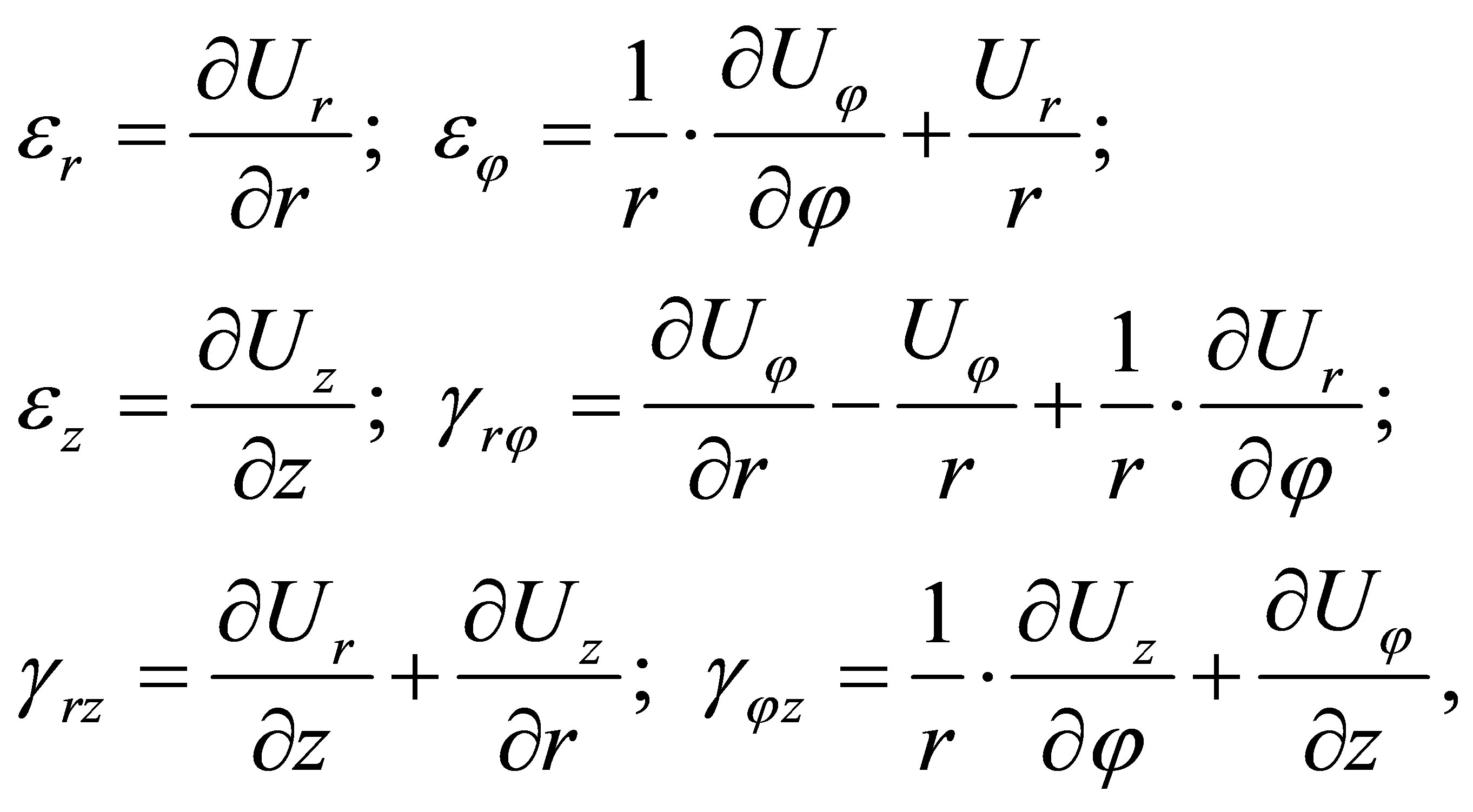 (3)
(3)
where 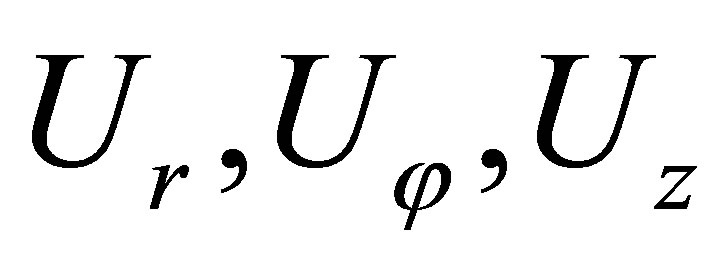 are components of the displacement vector
are components of the displacement vector 
Equations of the dynamic balance in the circular cylindrical system of coordinates [with the harmonic dependence from the time ] have the following appearance [1-4]:
] have the following appearance [1-4]:
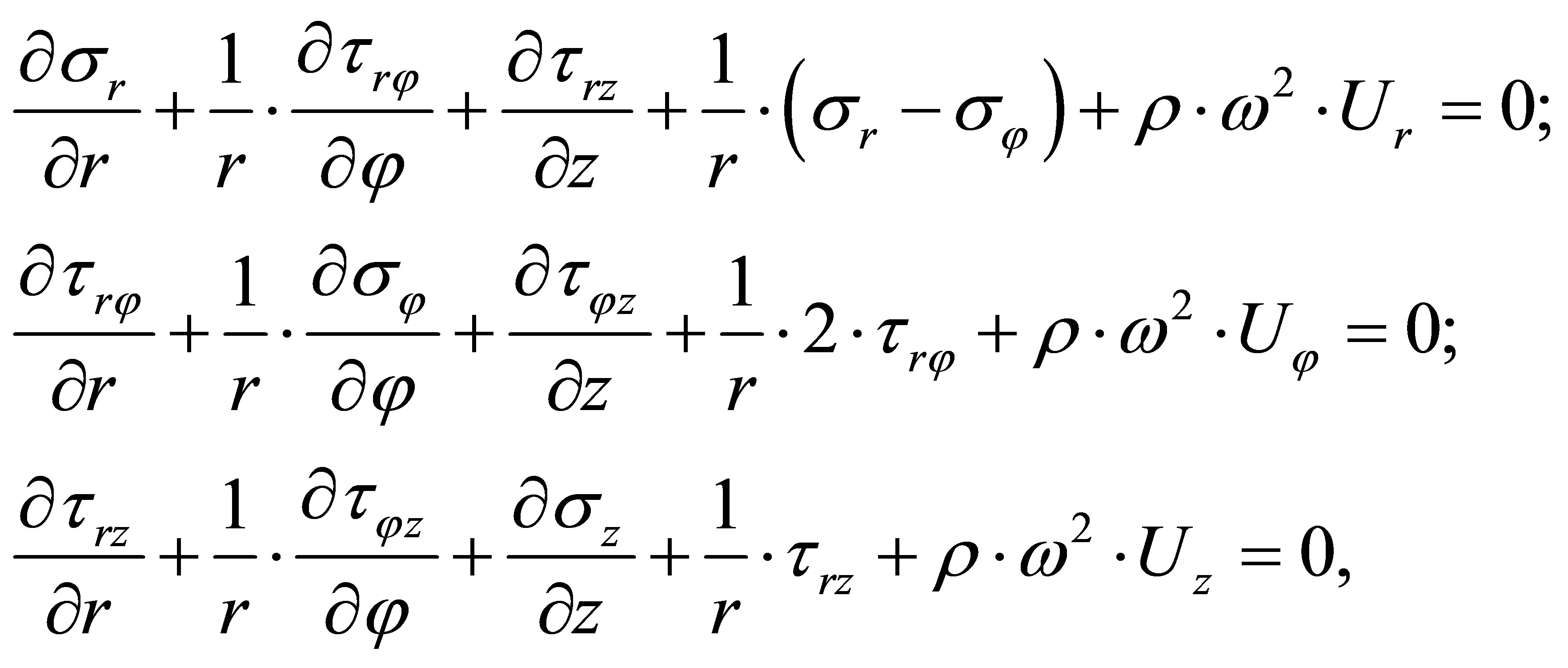 (4)
(4)
where
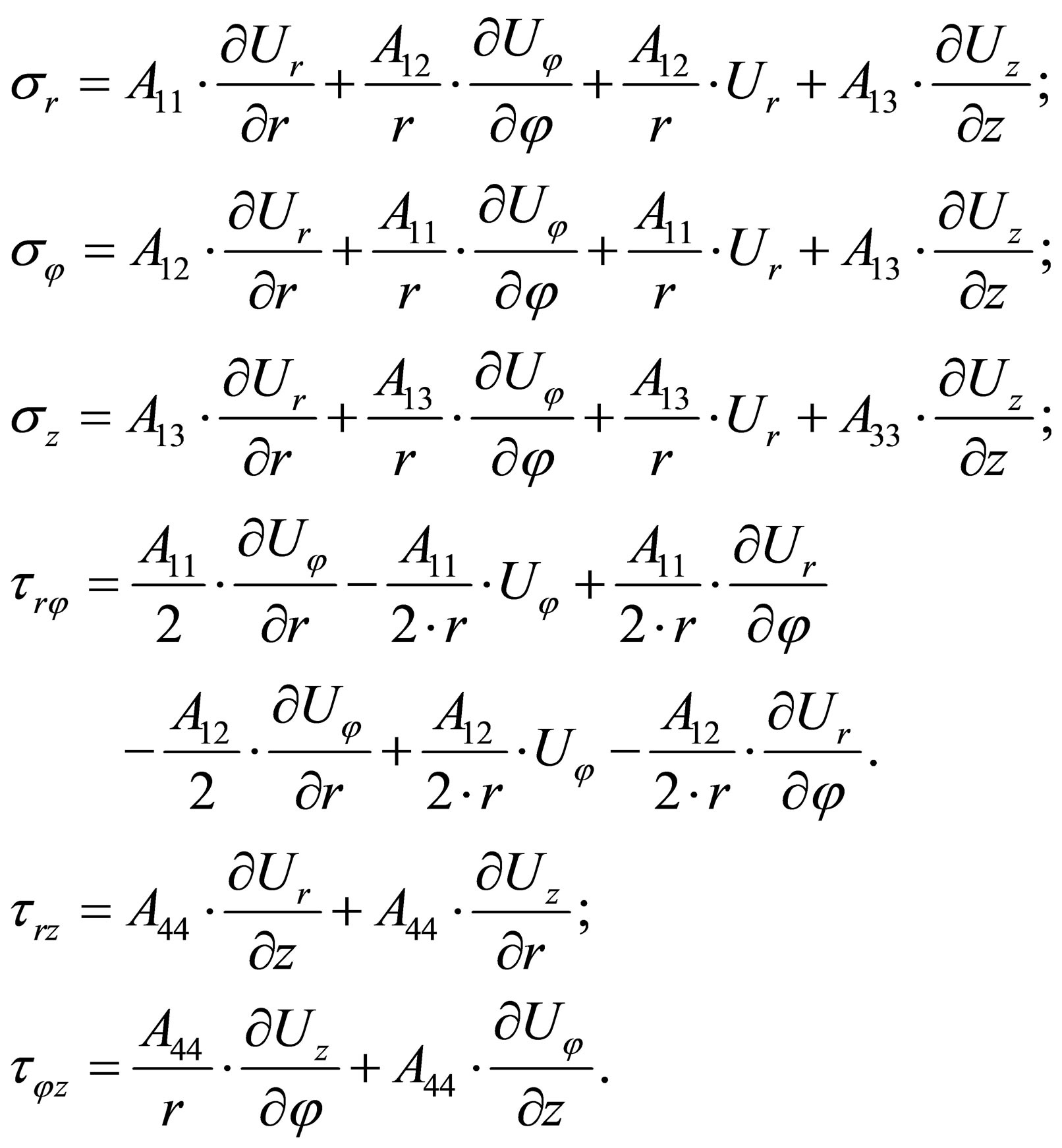 (5)
(5)
Components of the displacement vector 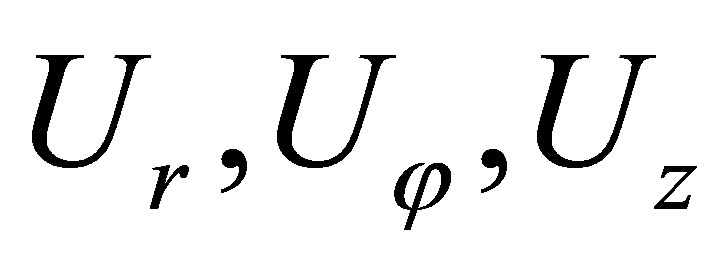 can be presented in the series form [2-4]:
can be presented in the series form [2-4]:
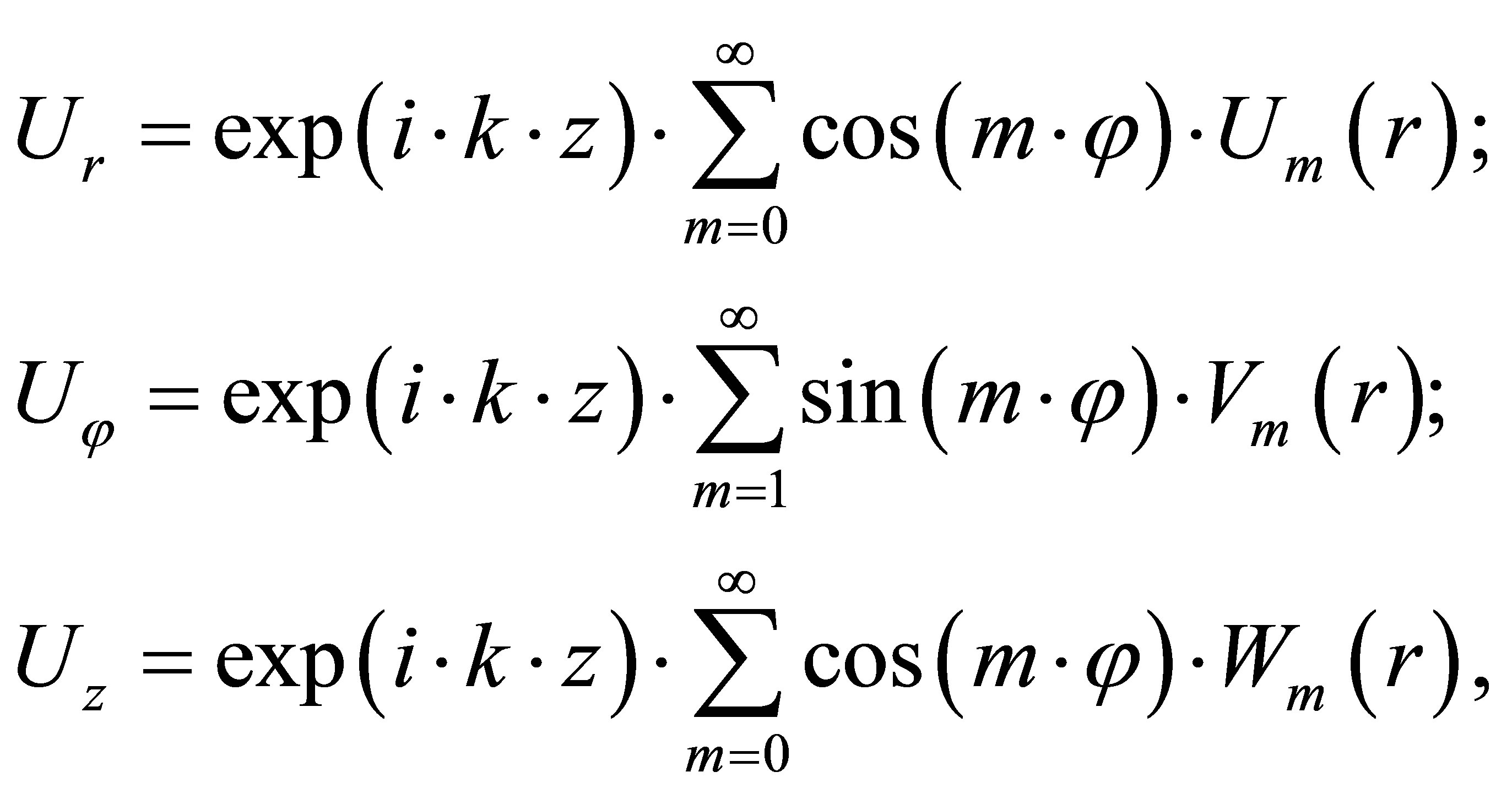 (6)
(6)
where  is the wave number of the elastic wave.
is the wave number of the elastic wave.
Then we substituted (4) in (5), we receive equations of the dynamic balance in displacements [2-4]:
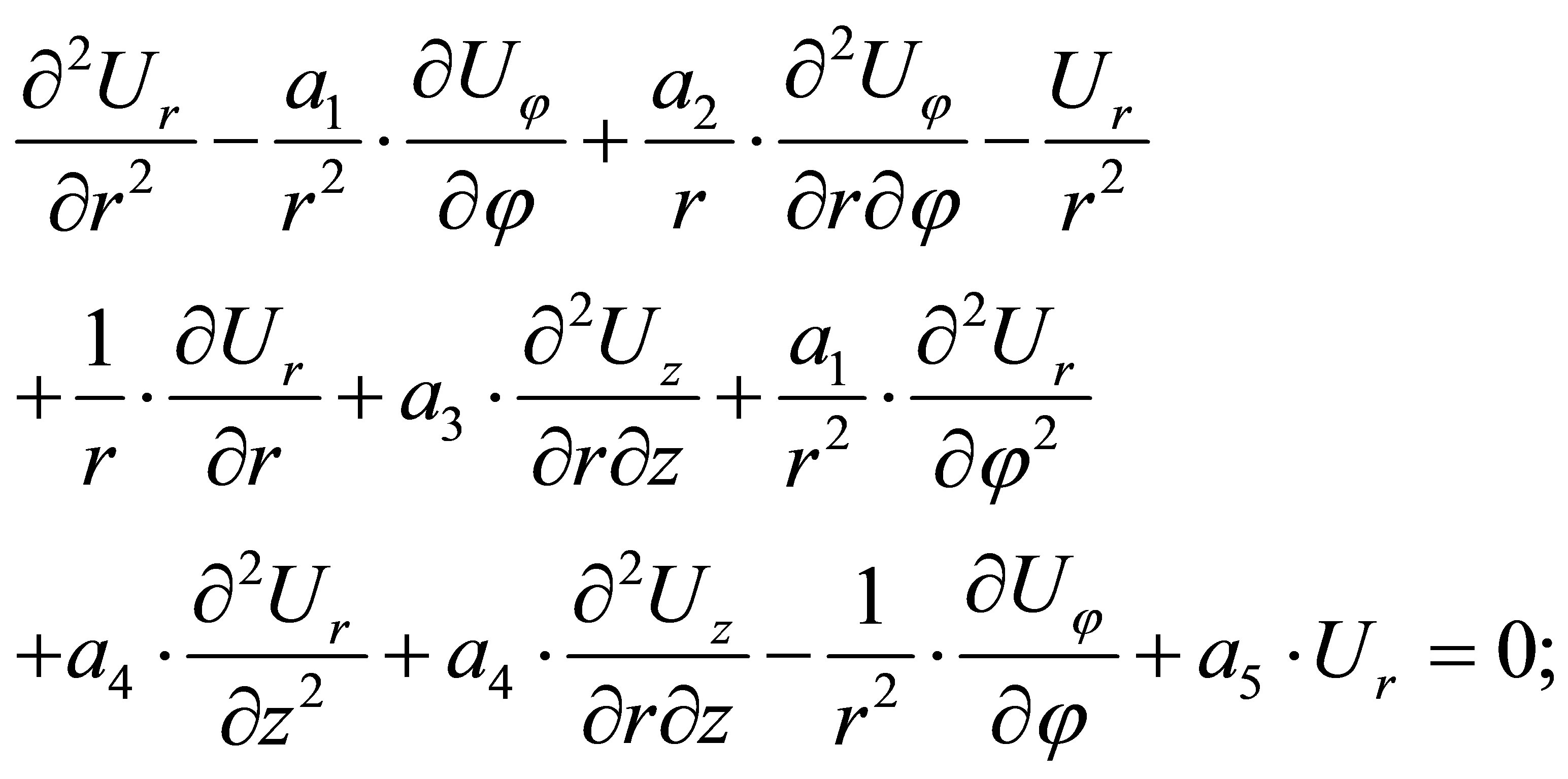 (7)
(7)
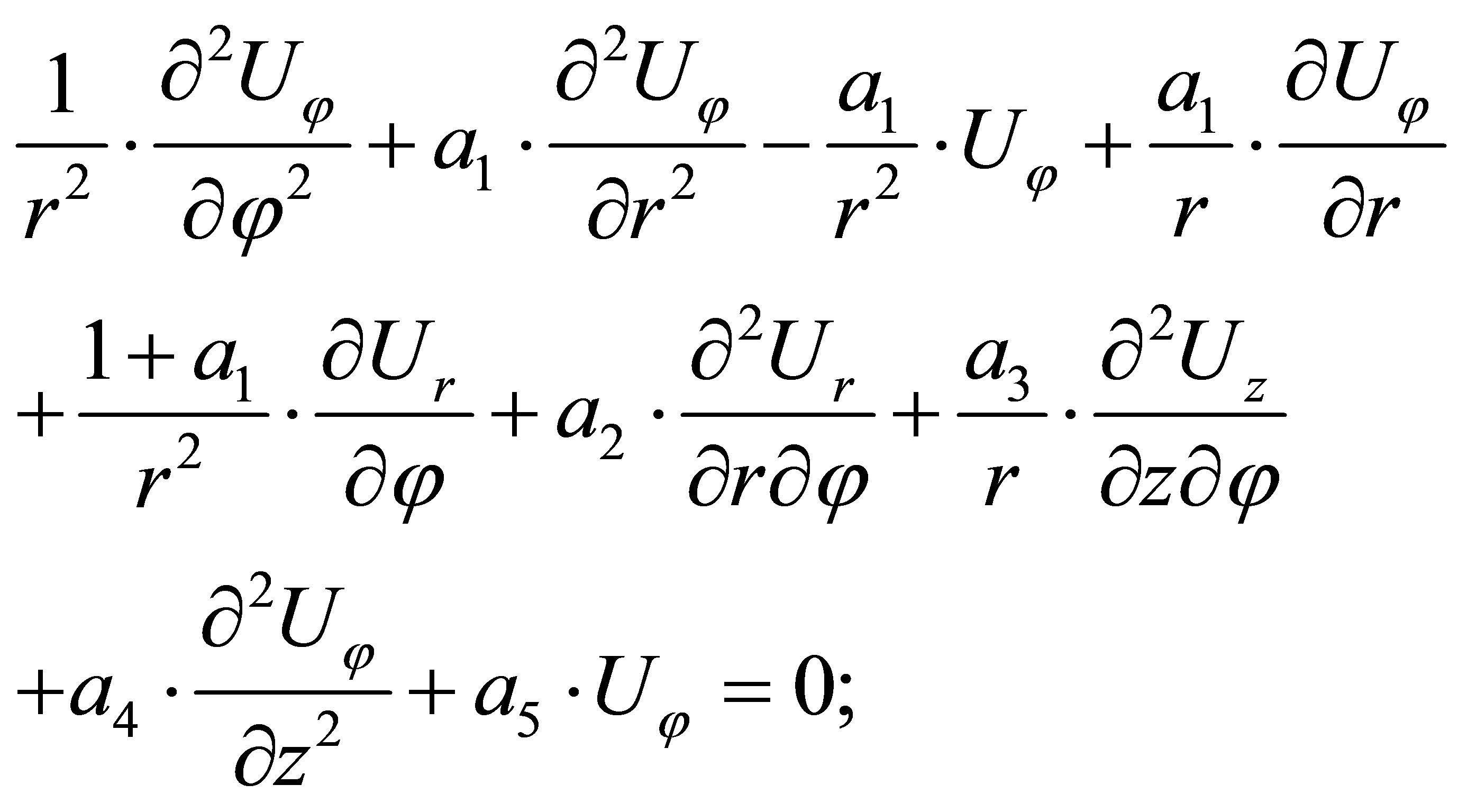 (8)
(8)
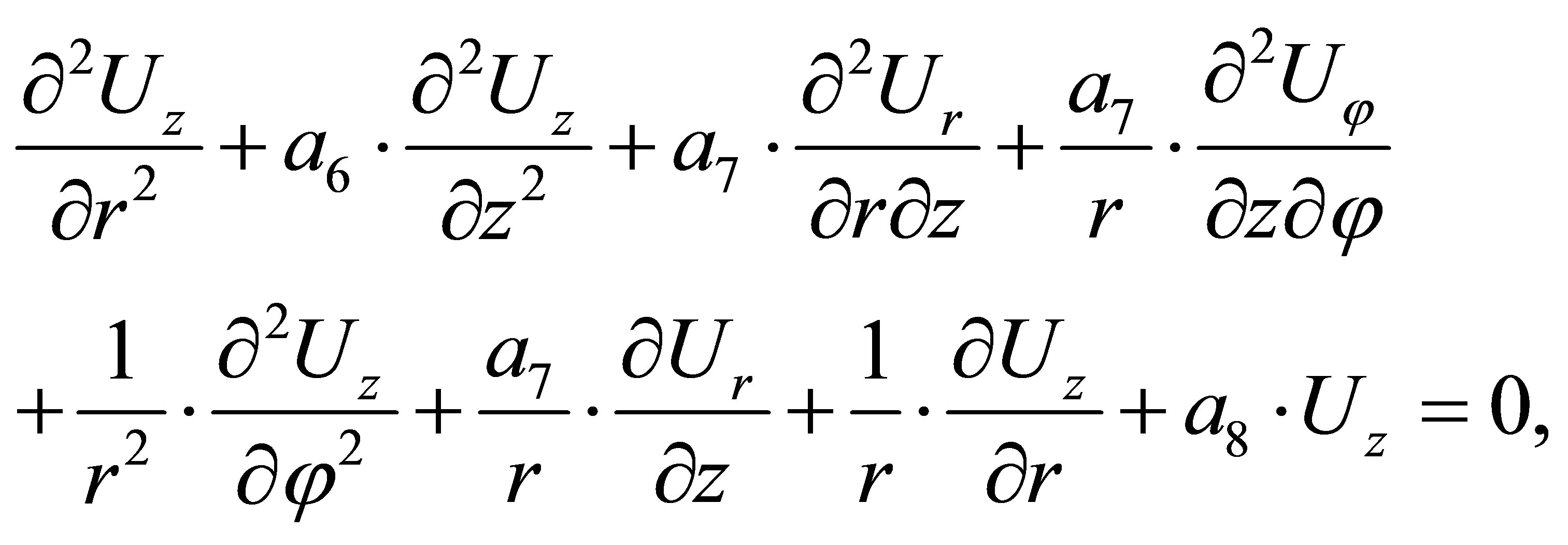 (9)
(9)
where
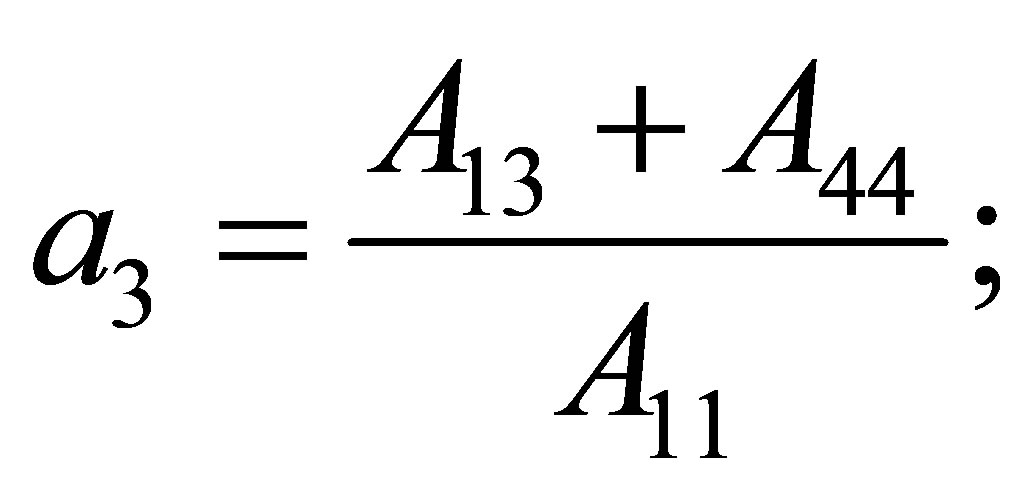

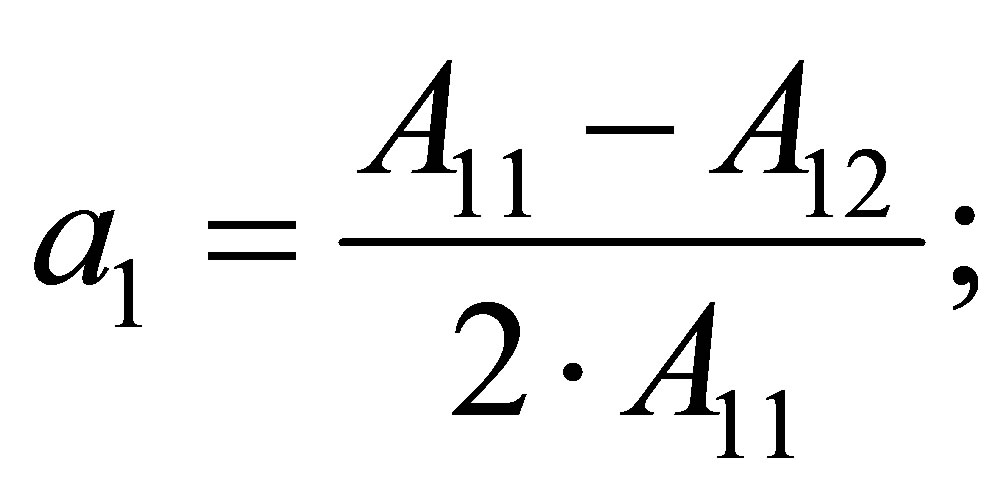
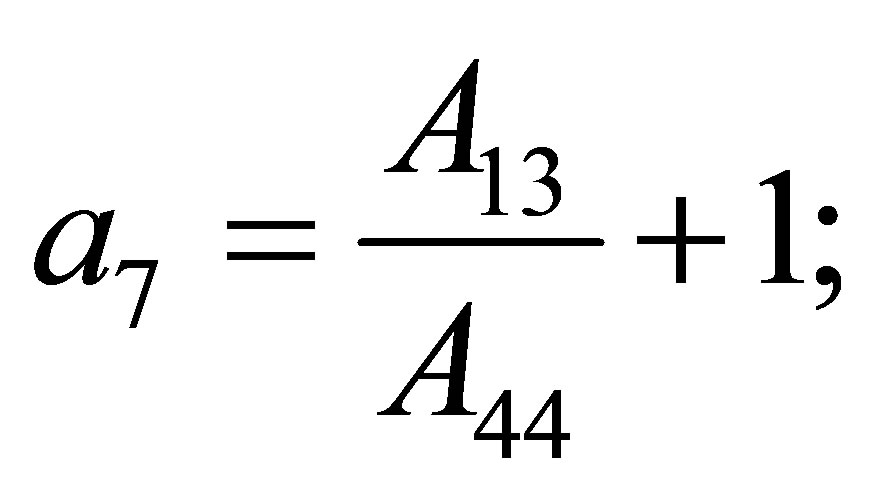
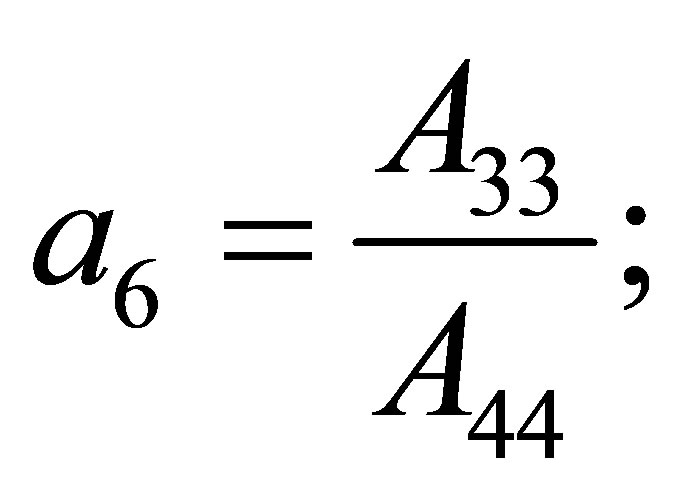
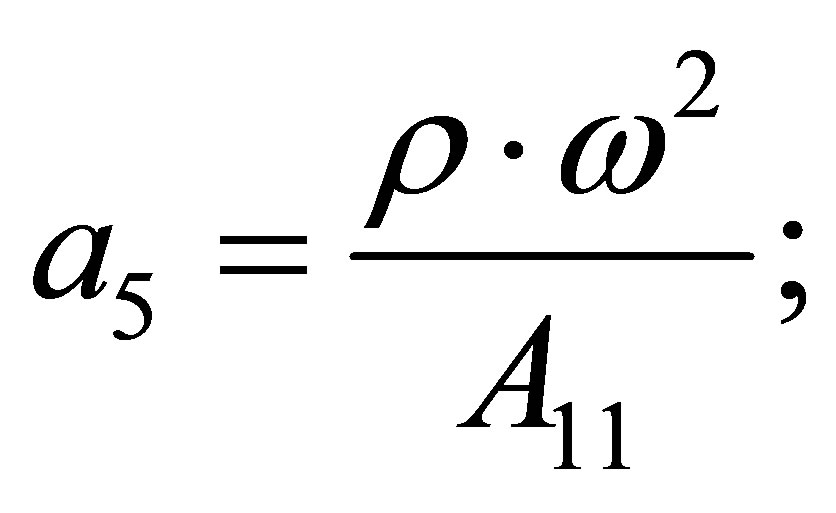
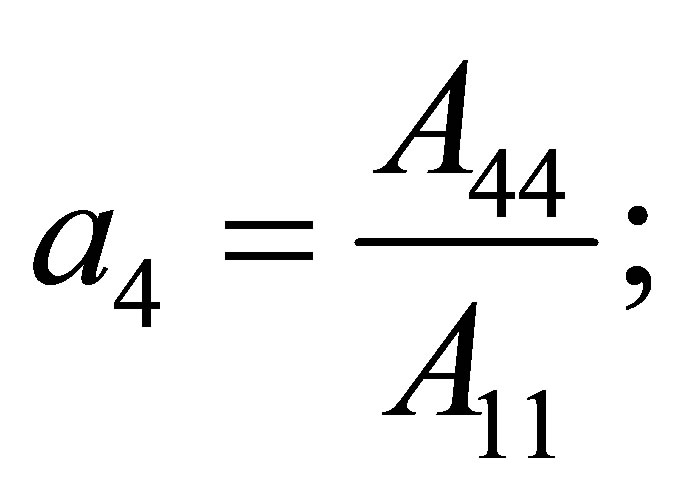
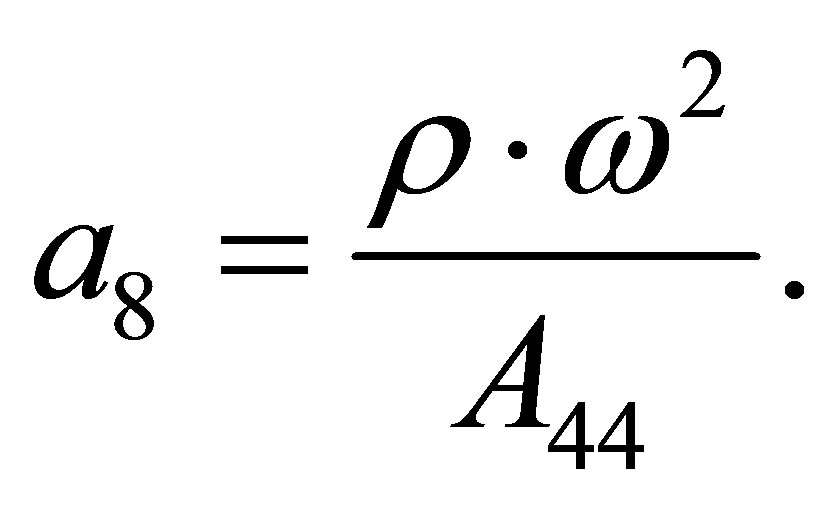
Now if components of the displacement vector 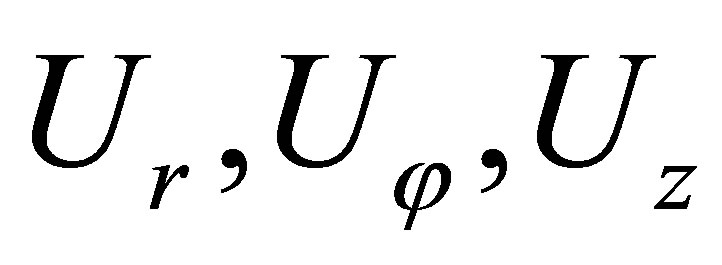 taken from (6) substitute in (7)-(9), then we receive following equations for radial functions
taken from (6) substitute in (7)-(9), then we receive following equations for radial functions 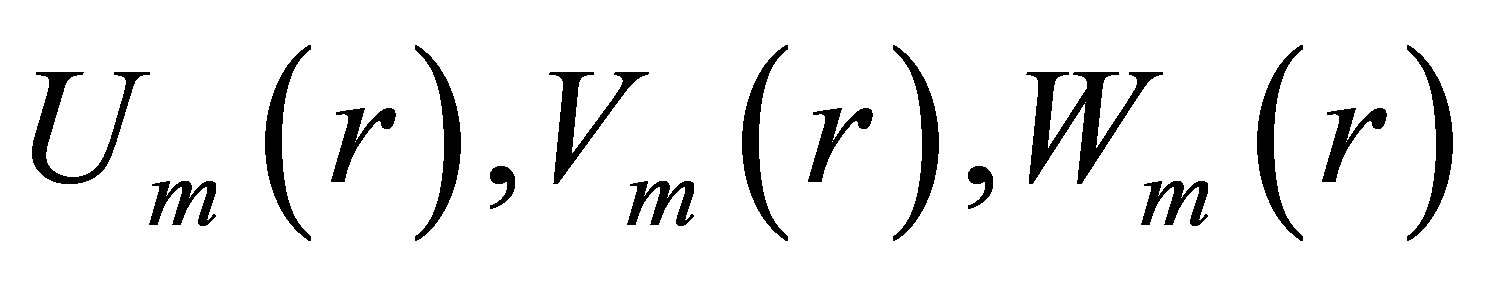 [2-4]:
[2-4]:
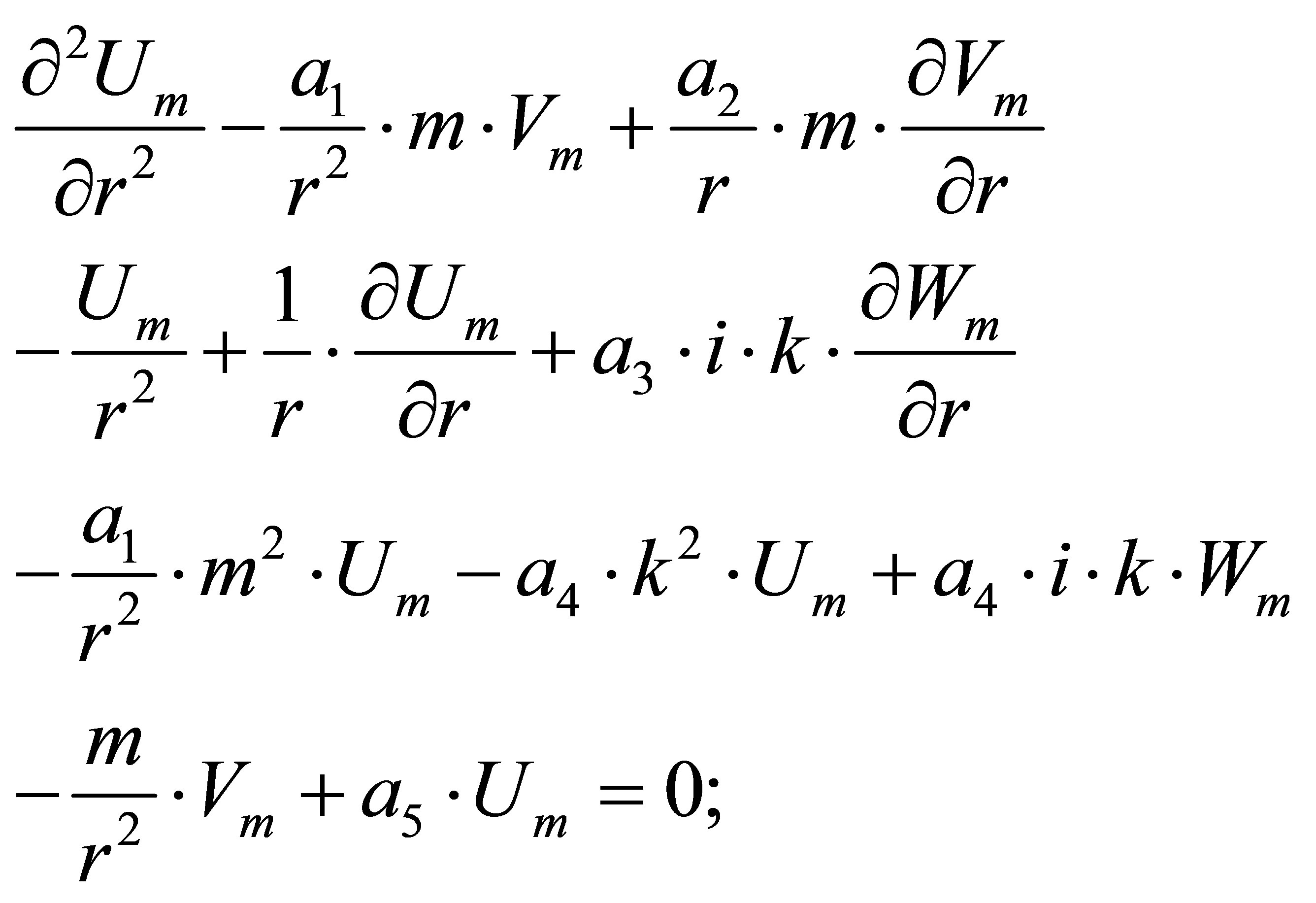 (10)
(10)
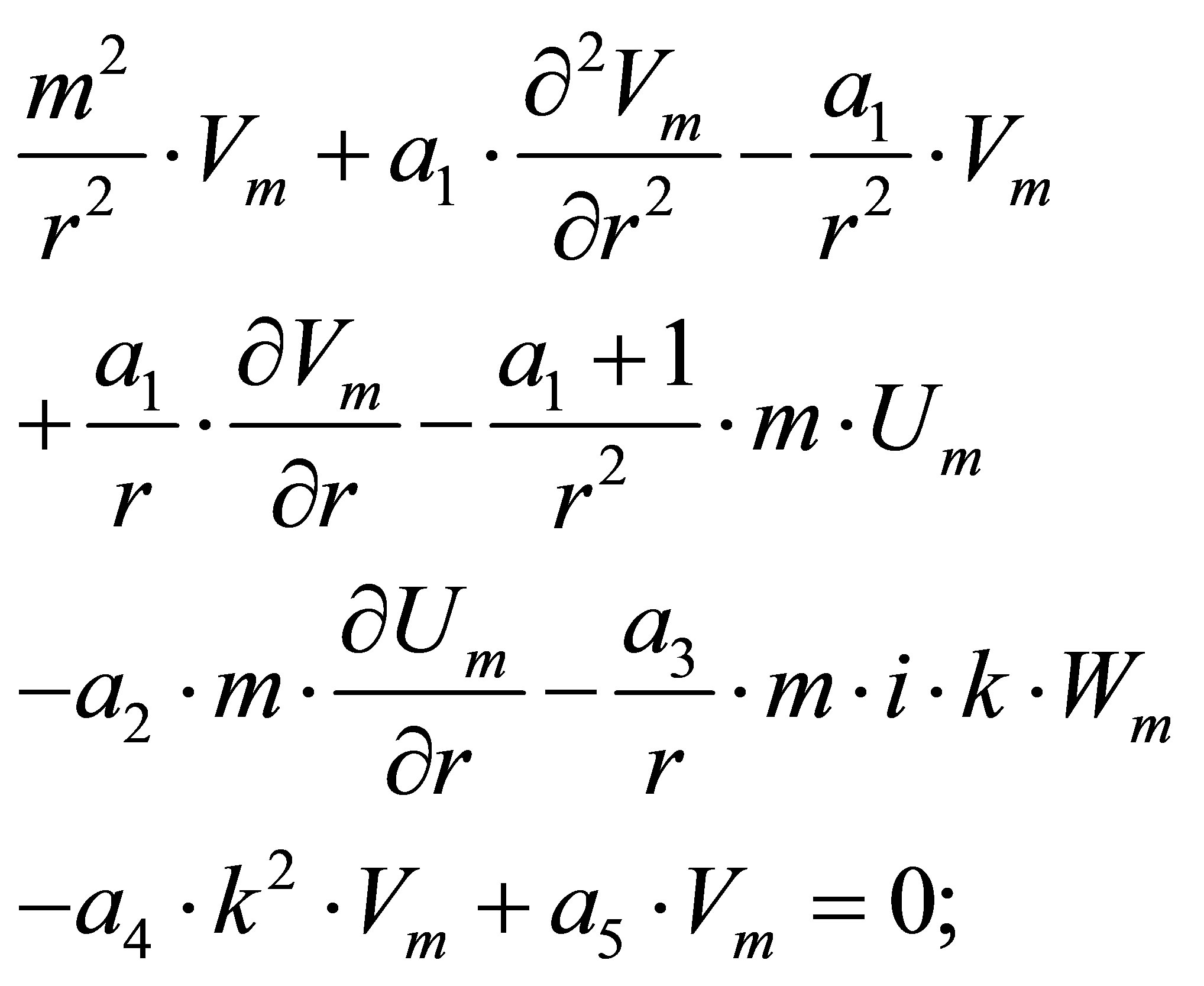 (11)
(11)
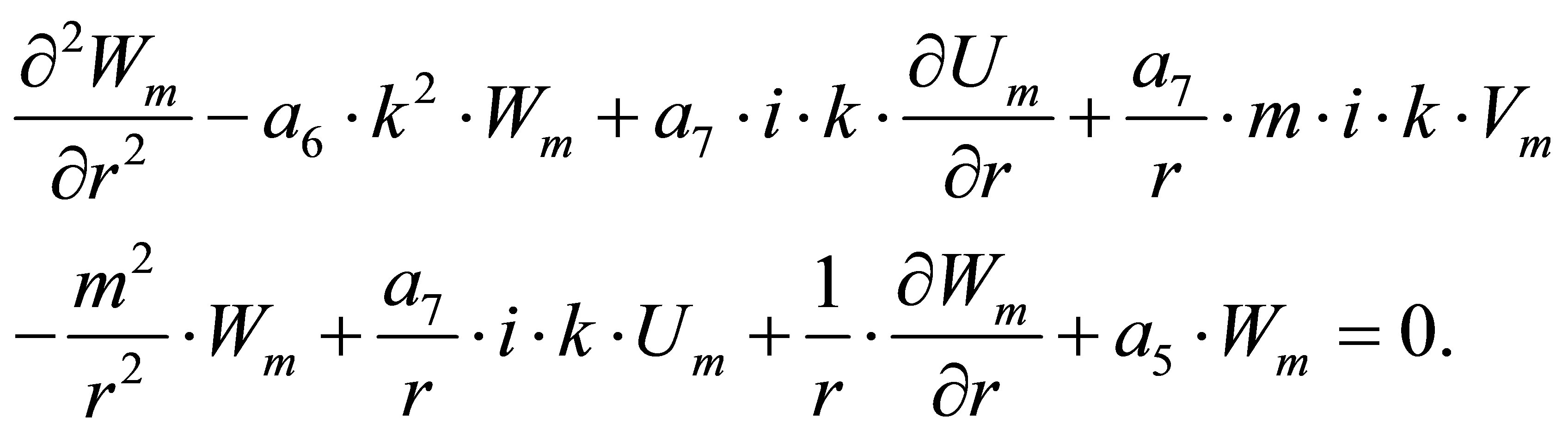 (12)
(12)
Boundary conditions: normal 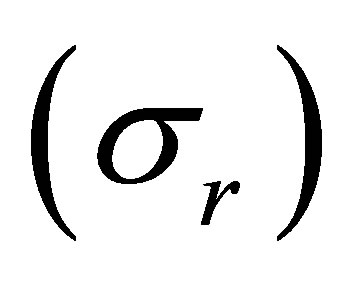 and tangent
and tangent 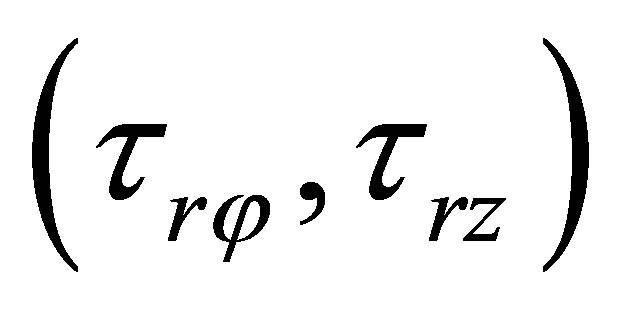 stresses are equal zero at external
stresses are equal zero at external 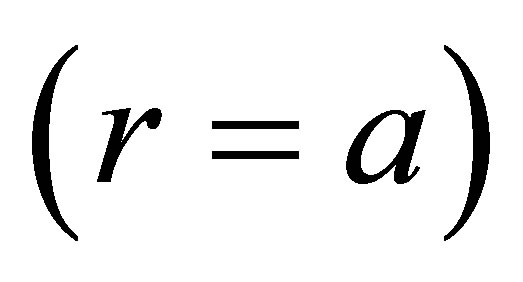 and internal
and internal 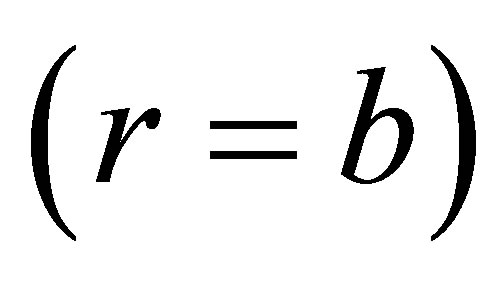 surfaces of the elastic shell are added to equations (10)-(12) [2-4]:
surfaces of the elastic shell are added to equations (10)-(12) [2-4]:
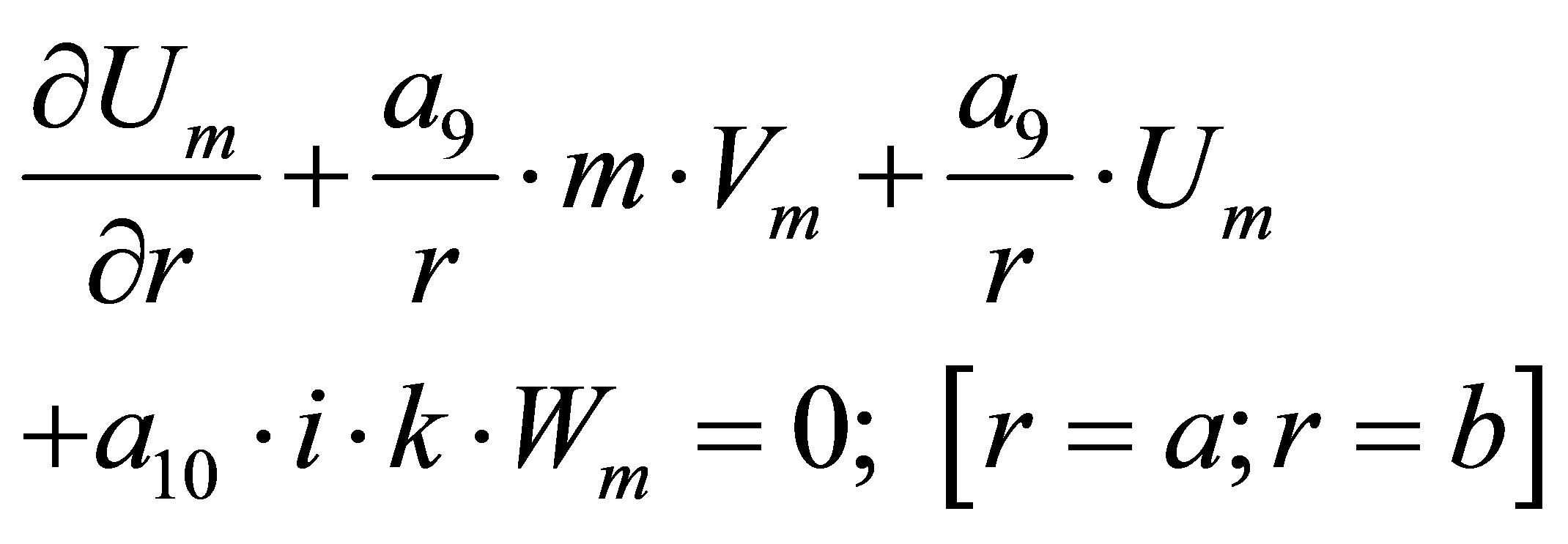 (13)
(13)
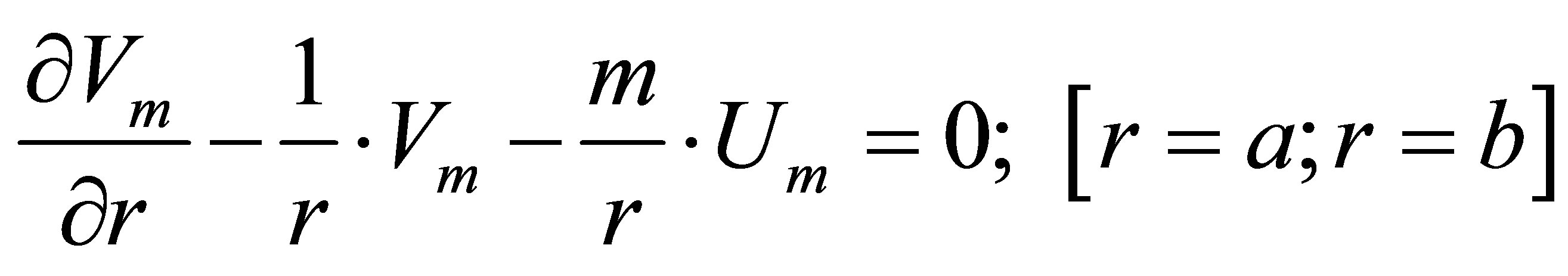 (14)
(14)
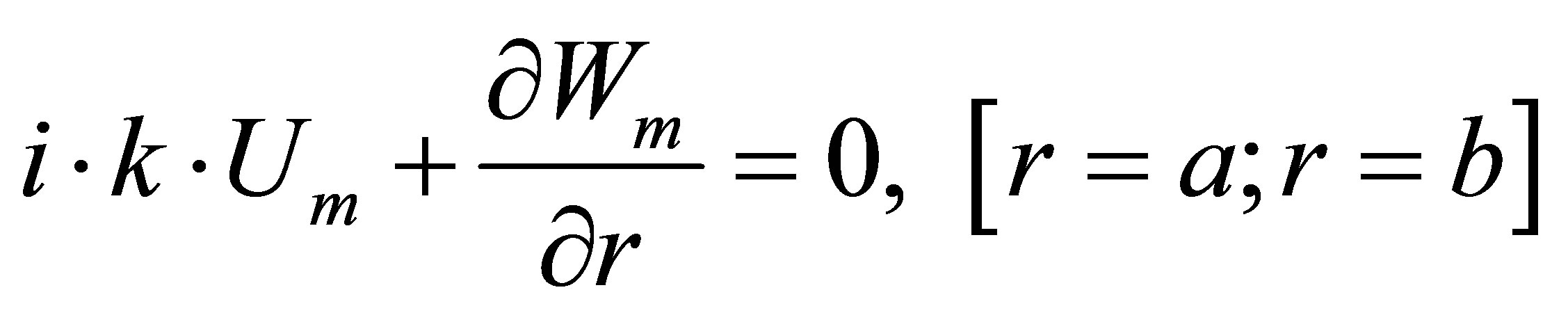 (15)
(15)
where
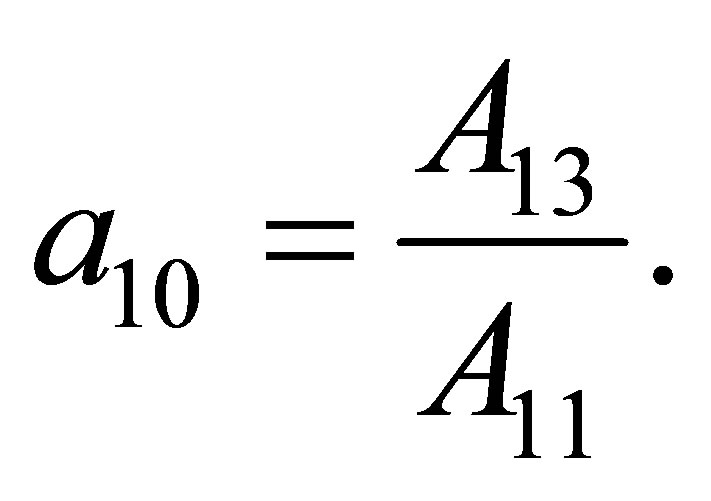
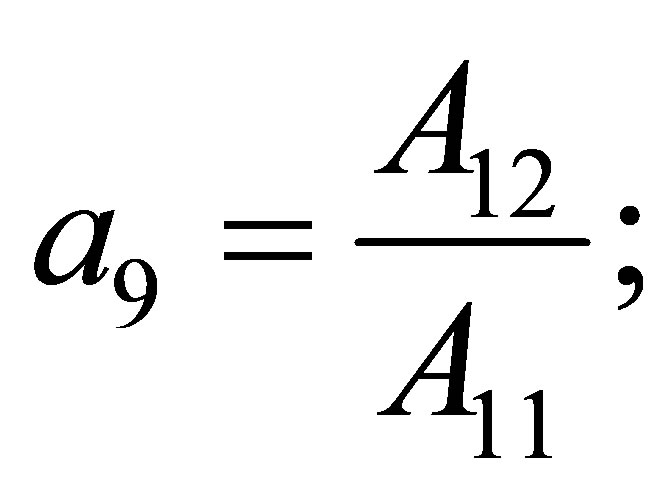
3. Hypothesis of Thin Shells
The fellow parameter
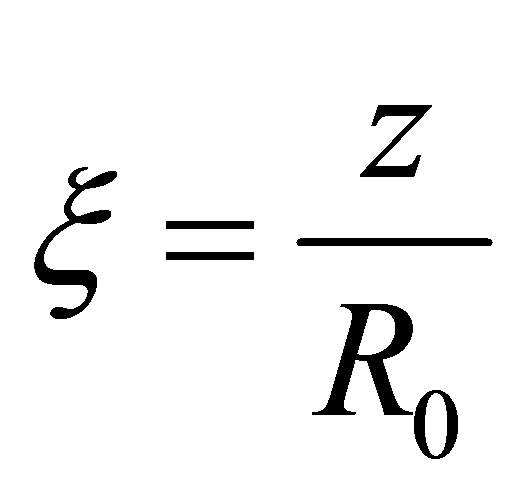
can be used for thin shells, where
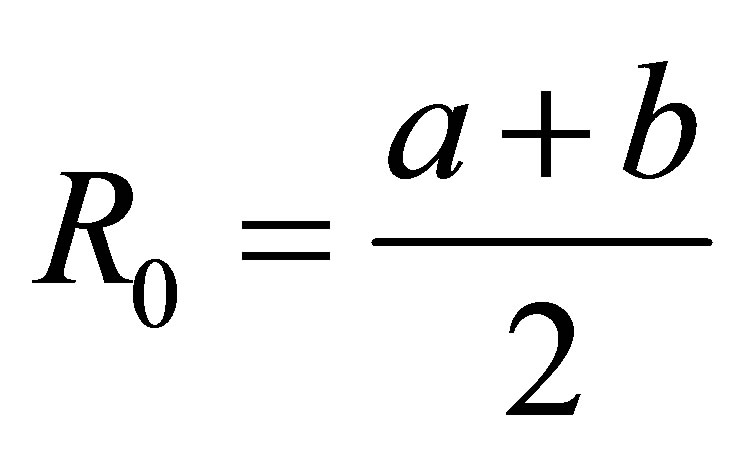
is middle radius and 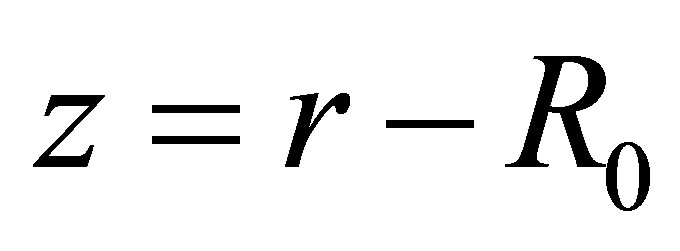 is the coordinate taking from the middle surface [2-5]:
is the coordinate taking from the middle surface [2-5]:
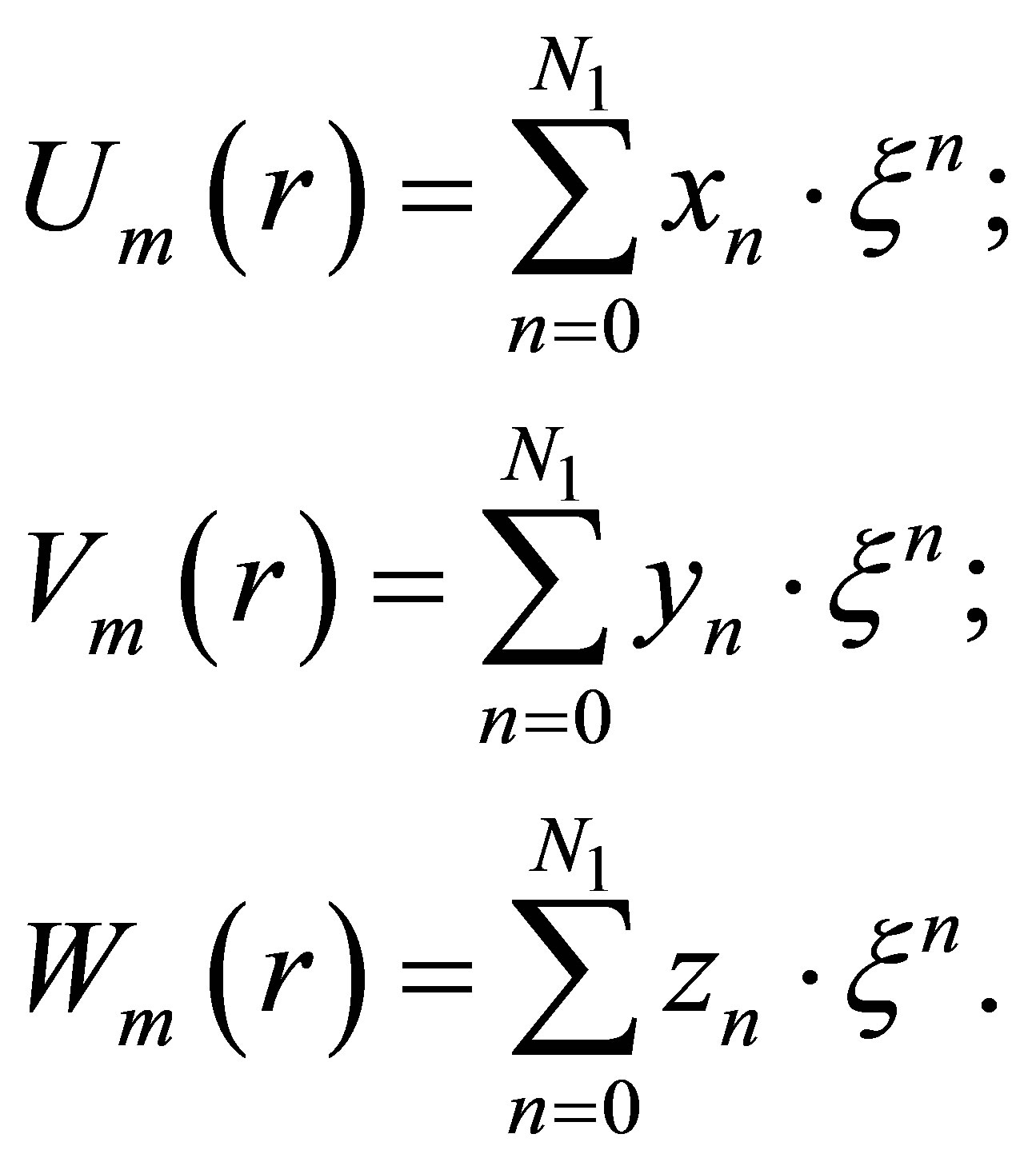 (16)
(16)
We substitute decompositions in boundary Conditions (13)-(15) and 6 equations relative to 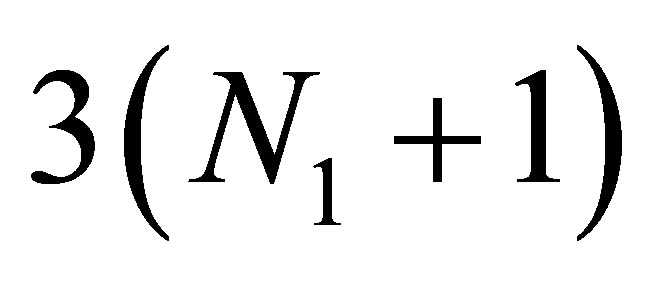 unknown coefficients
unknown coefficients 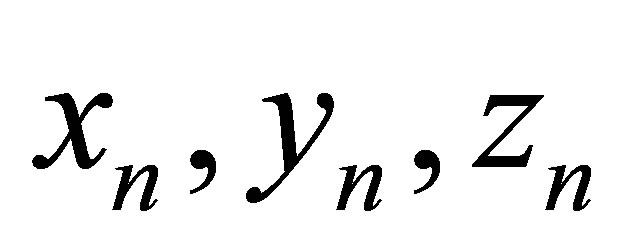 [2-4]:
[2-4]:
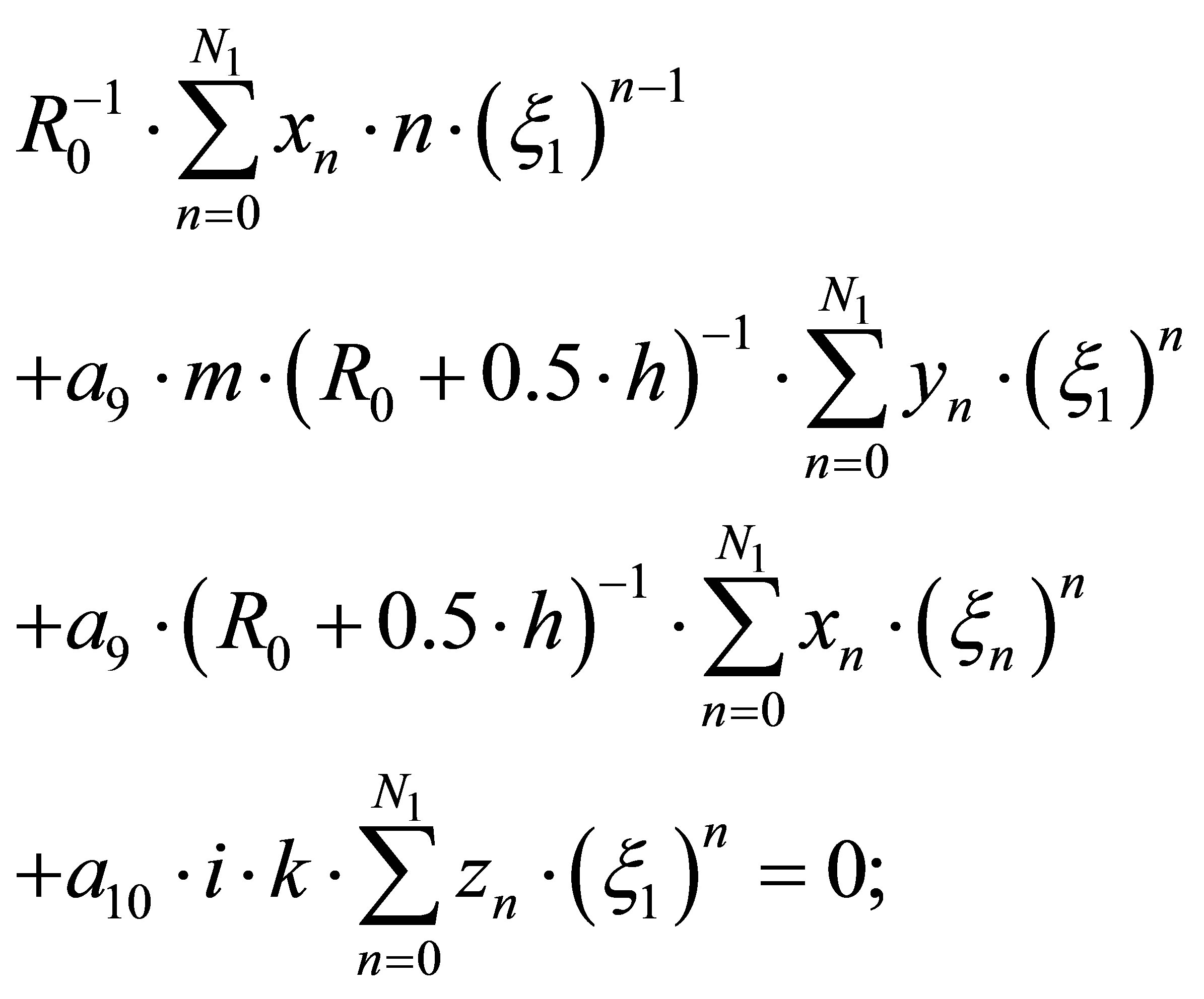 (17)
(17)
 (18)
(18)
 (19)
(19)
 (20)
(20)
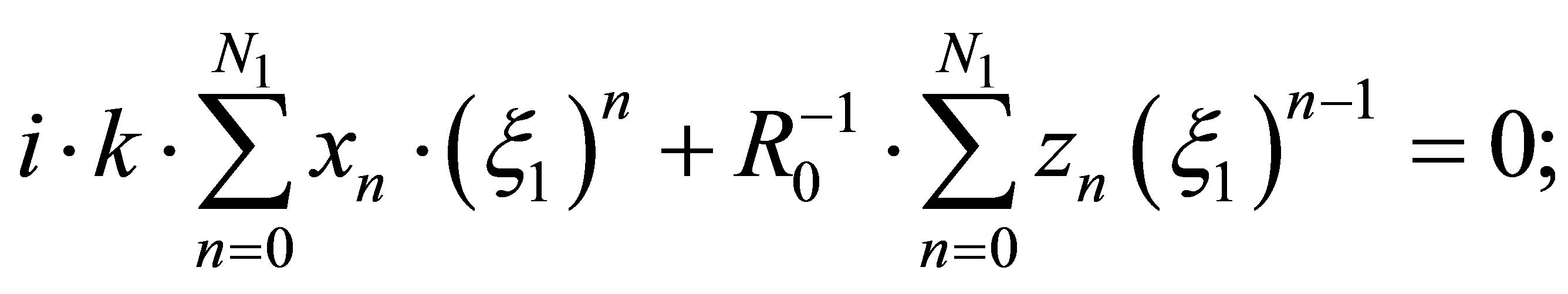 (21)
(21)
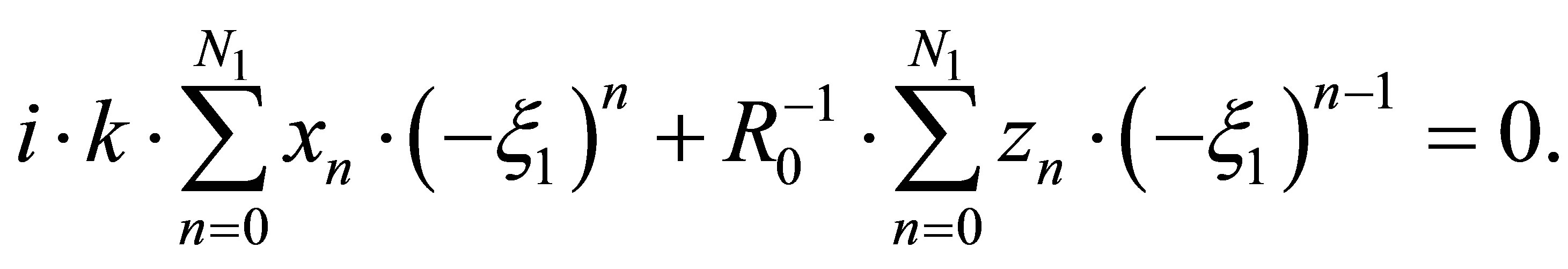 (22)
(22)
The rest of equations can be received, by substitution of decompositions (16) in equations (10)-(12) and by equated of coefficients at identical powers  [2-4]:
[2-4]:
 (23)
(23)
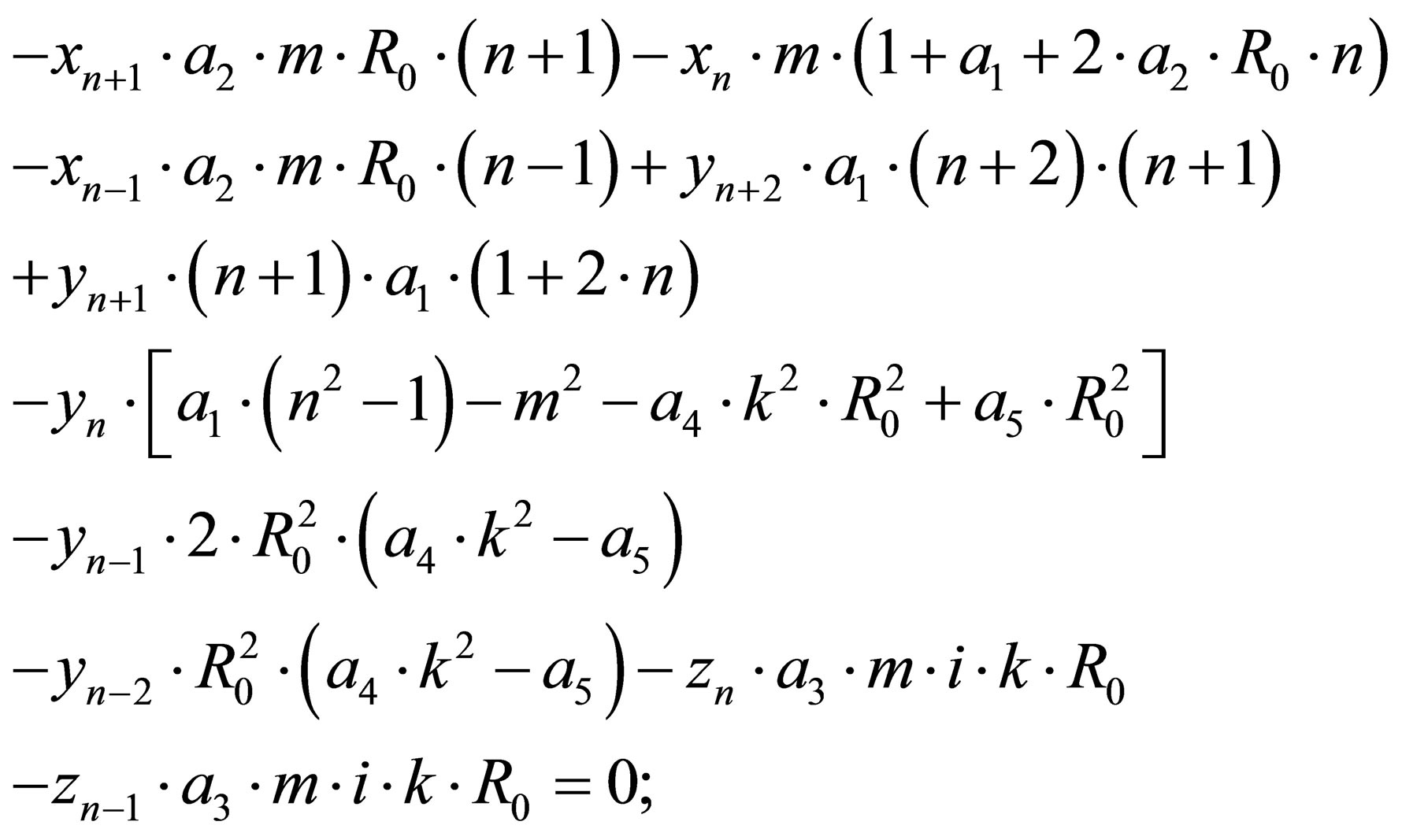 (24)
(24)
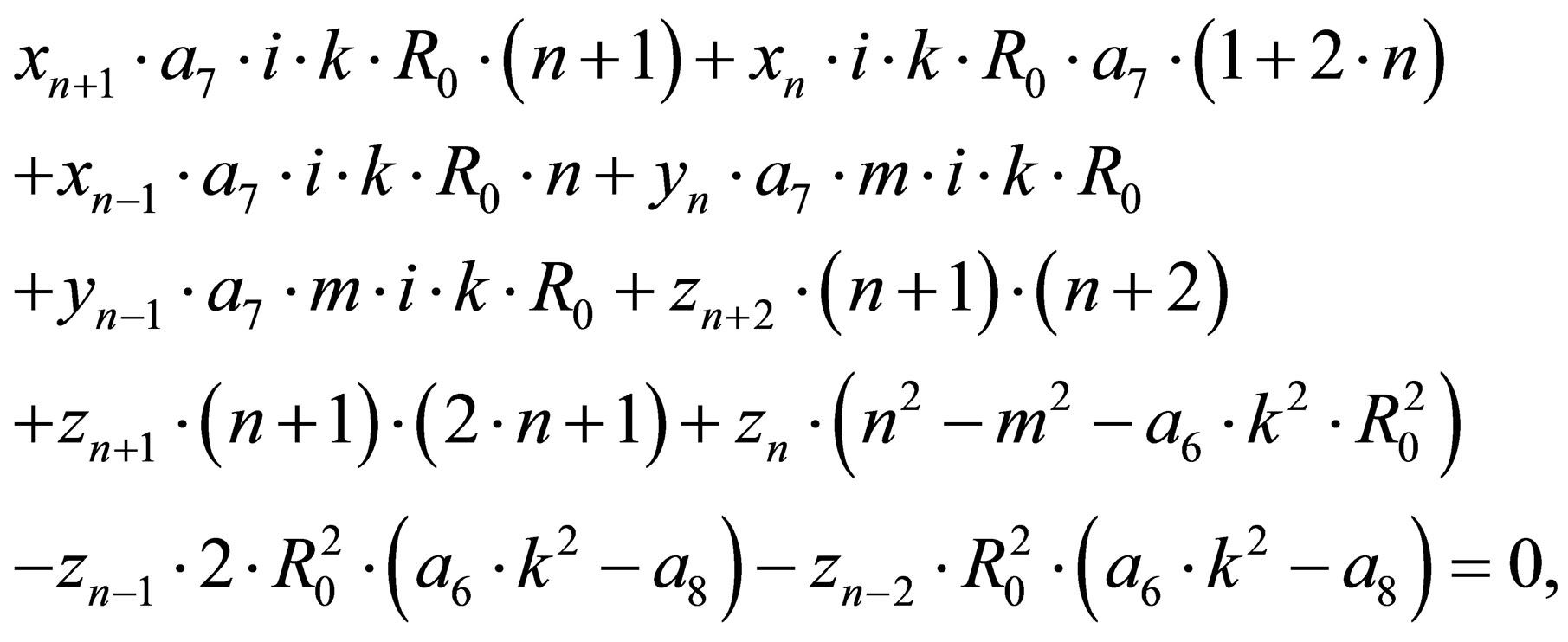 (25)
(25)
where  .
.
It is necessary to use 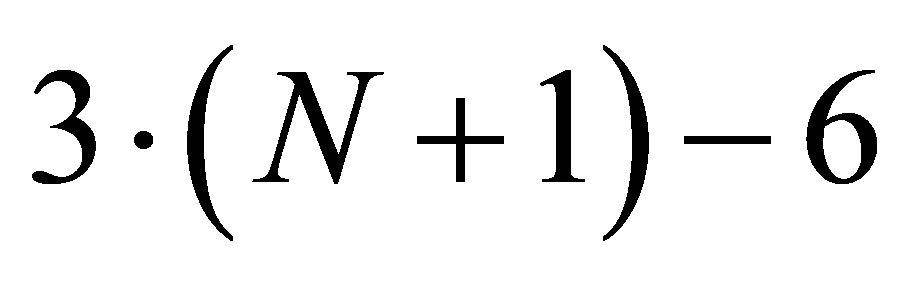 of equations (23)-(25) and for
of equations (23)-(25) and for 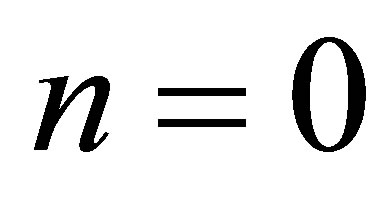 and
and  coefficients with negative indexes are equal to zero. Then in common with the equations (17)-(22) the homogeneous system of
coefficients with negative indexes are equal to zero. Then in common with the equations (17)-(22) the homogeneous system of 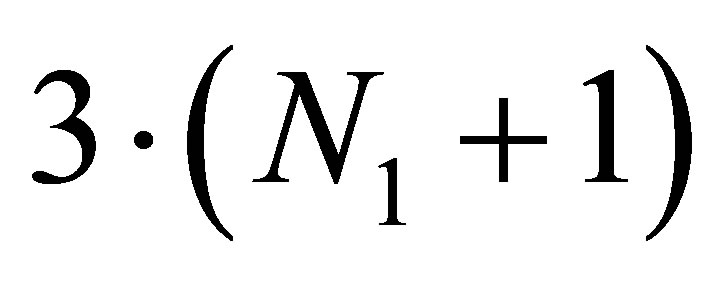 equations relative to coefficients
equations relative to coefficients 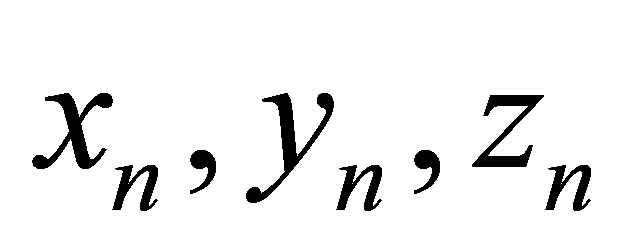 is formed. Afterwards, we expand the determinant of this system and let this determinant is equal zero we receive the characteristic equation for wave numbers
is formed. Afterwards, we expand the determinant of this system and let this determinant is equal zero we receive the characteristic equation for wave numbers  of elastic waves of the mode
of elastic waves of the mode ![]() in the transversely isotropic cylindrical shell.
in the transversely isotropic cylindrical shell.
Now we sell pay attention to elastic waves, which have axial symmetry: the dependence from the angle ![]() disappears. If vector of the shell displacement
disappears. If vector of the shell displacement  has not of the component
has not of the component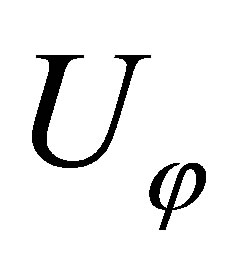 , then we have waves with the vertical polarization. In thin case components of strains
, then we have waves with the vertical polarization. In thin case components of strains 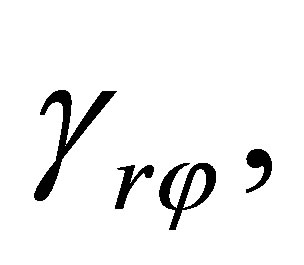
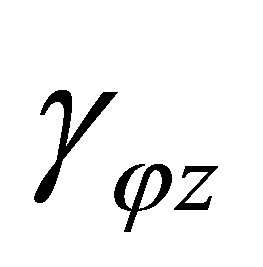 and tangent stresses
and tangent stresses 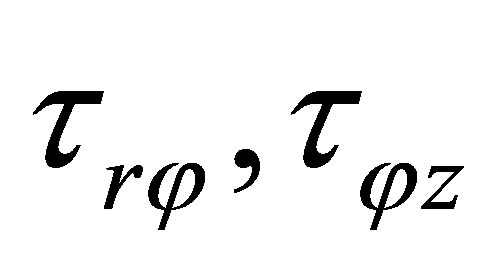 are equal to zero, but stresses
are equal to zero, but stresses  and
and 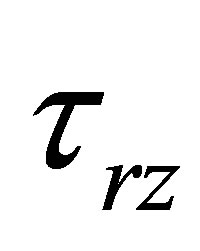 are equal [2-4]:
are equal [2-4]:
 (26)
(26)
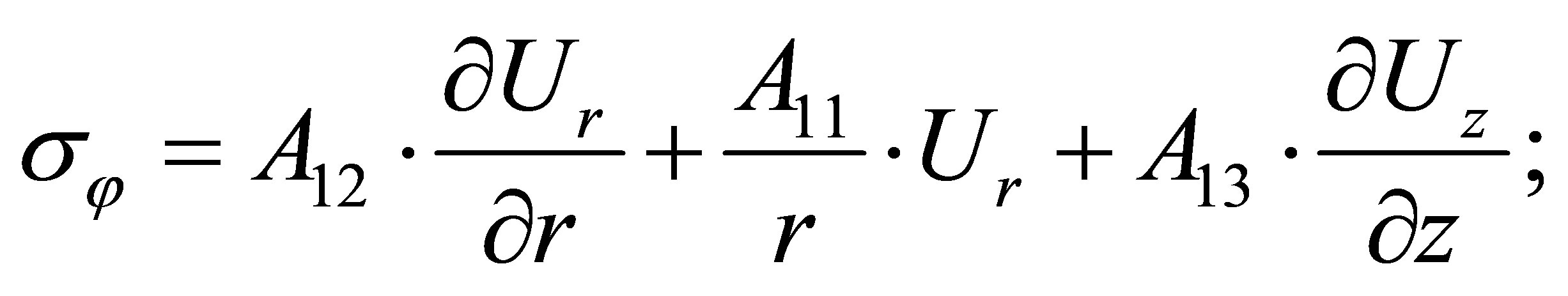 (27)
(27)
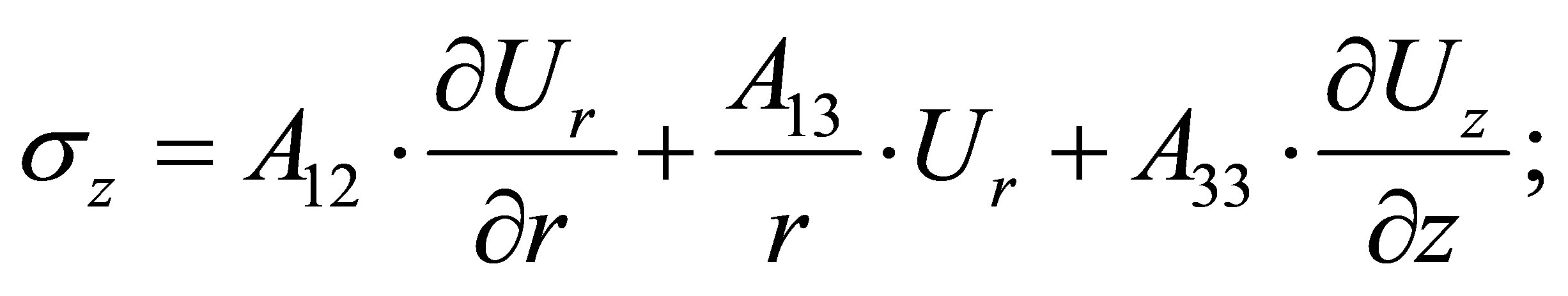 (28)
(28)
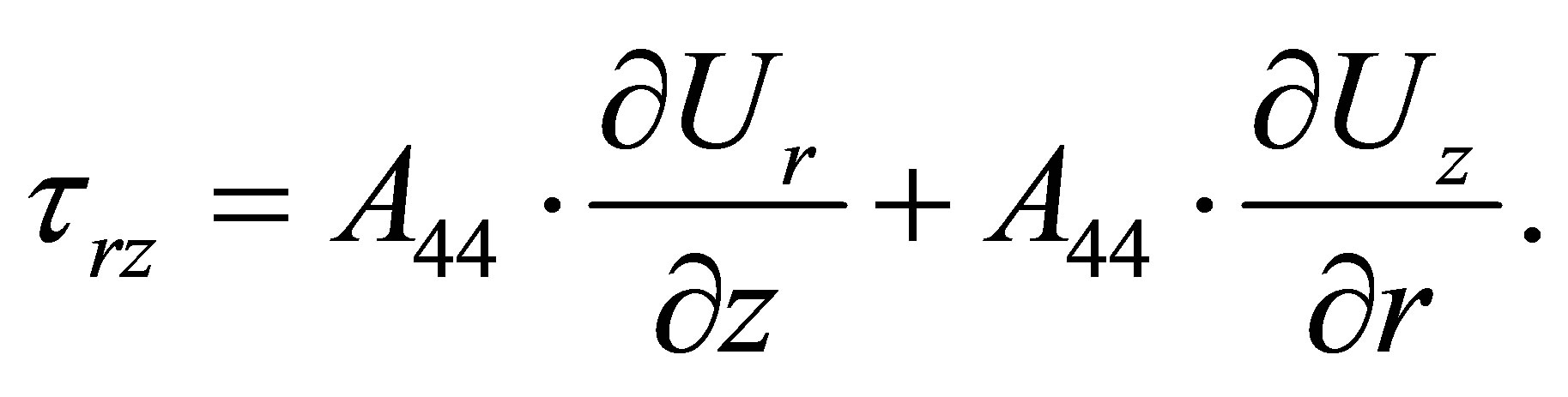 (29)
(29)
Equations of the dynamic balance (their only 2) have the following form [2-4]:
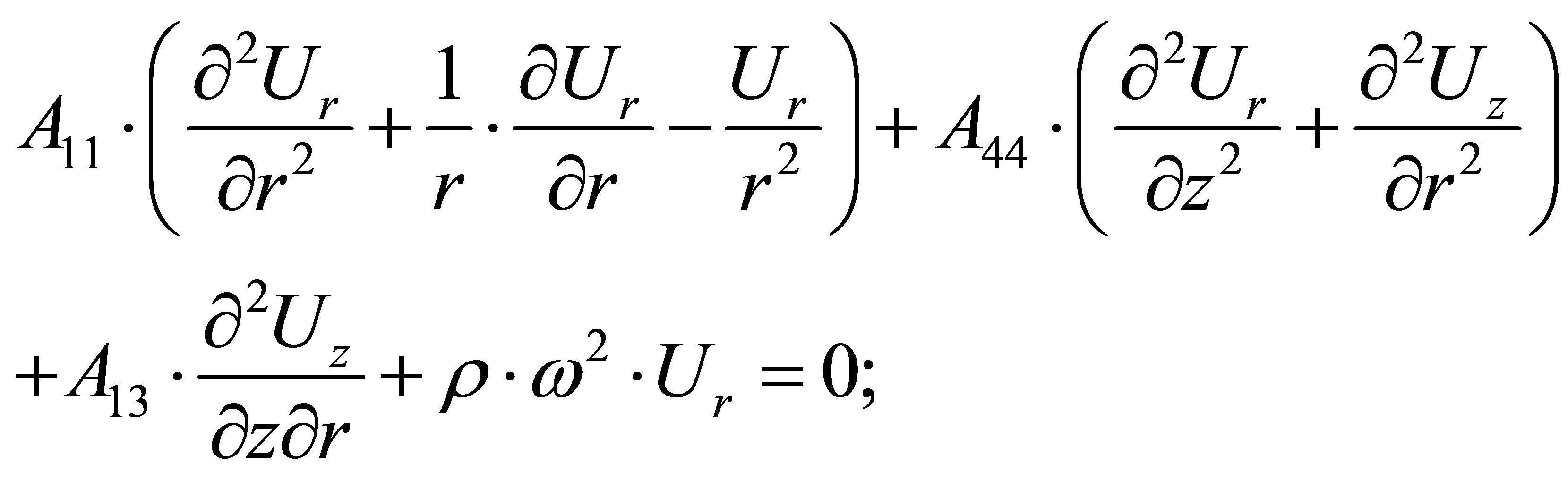 (30)
(30)
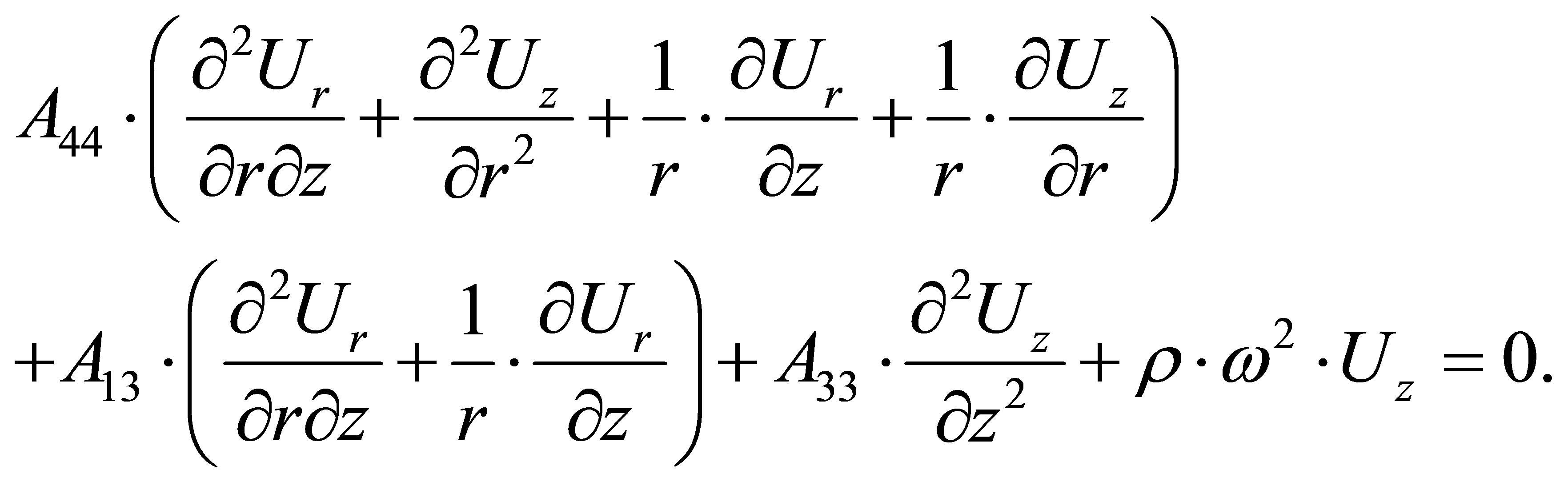 (31)
(31)
Displacements 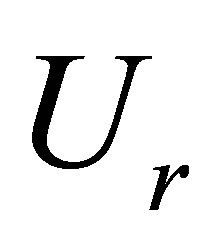 and
and 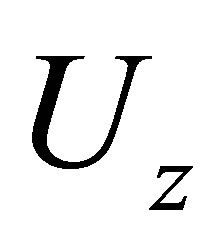 can be taken in the form [2-4]:
can be taken in the form [2-4]:
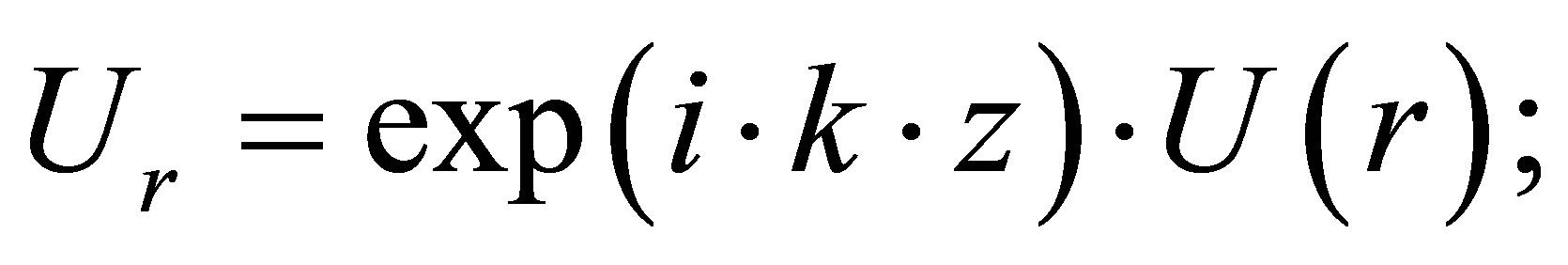 (32)
(32)
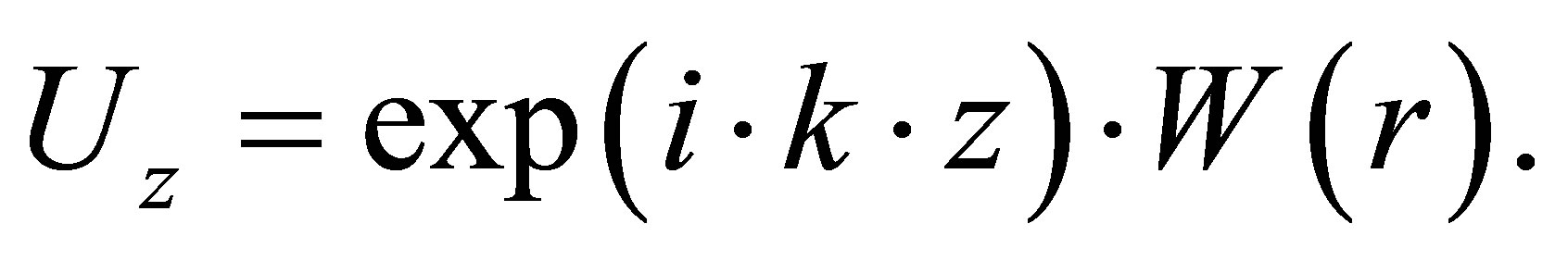 (33)
(33)
For the thin shell 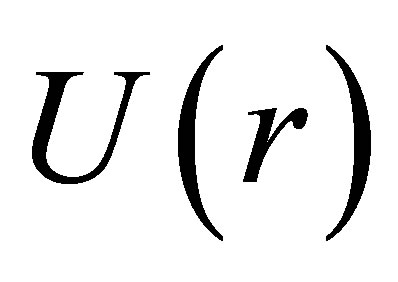 and
and  can be expanded in serieses:
can be expanded in serieses:
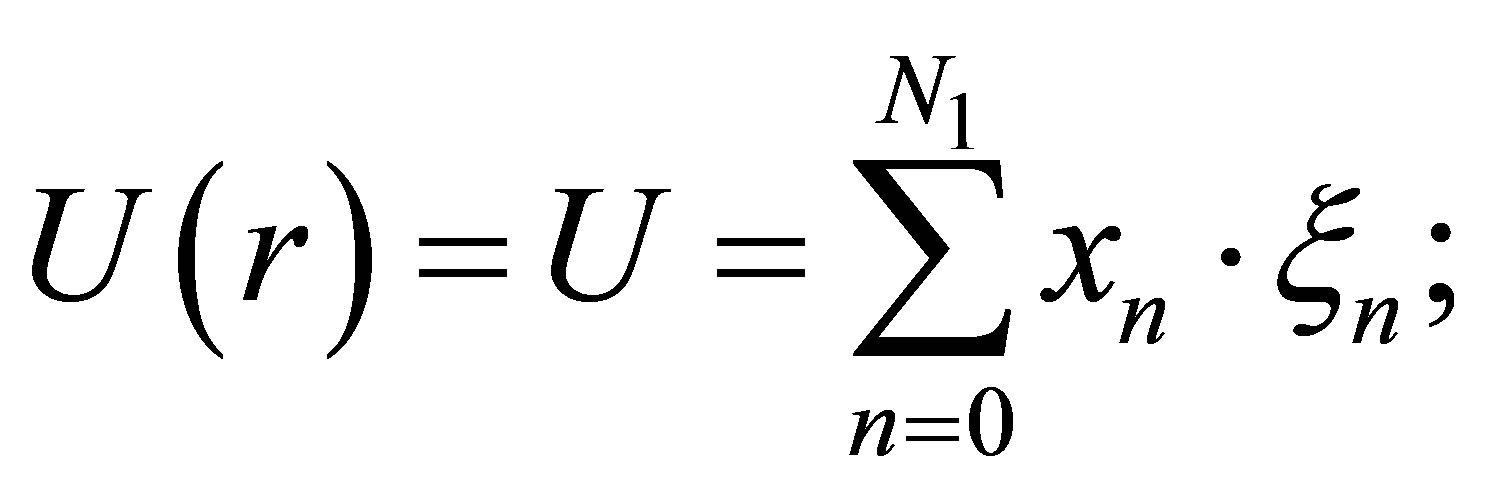 (34)
(34)
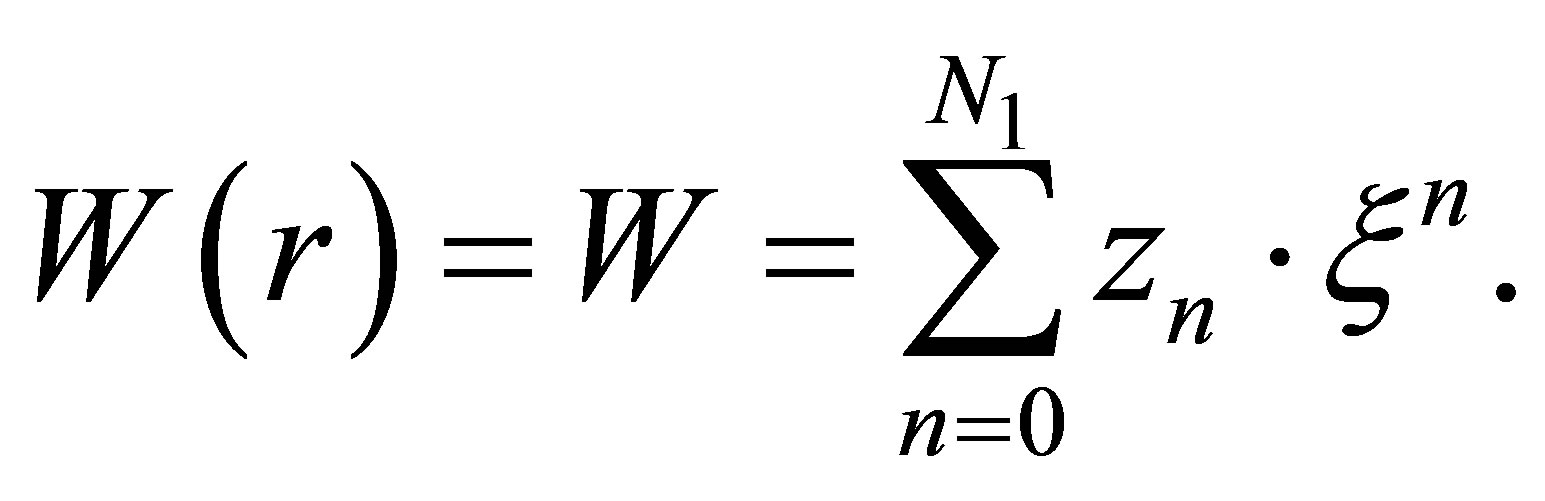 (35)
(35)
Boundary conditions (their only 2) can be expressed as [2-4]:
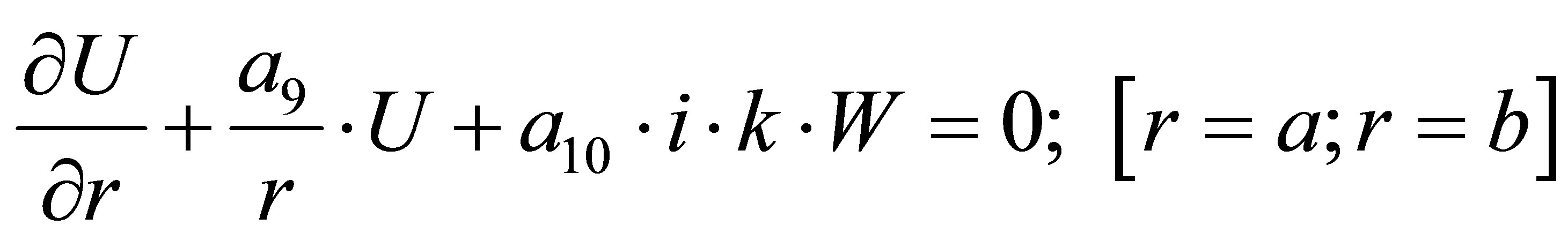 (36)
(36)
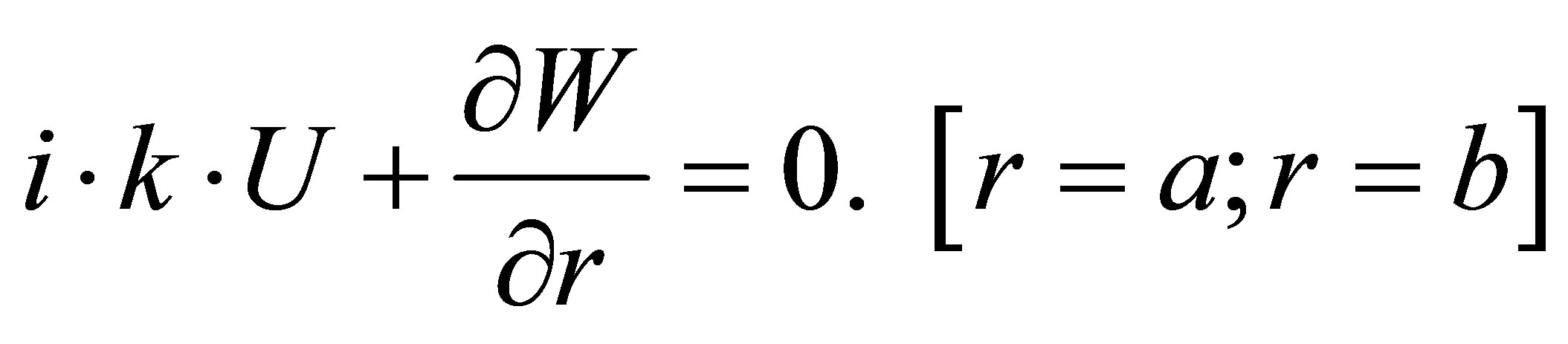 (37)
(37)
The substitution (32), (33) and (34), (35) into boundary conditions (36), (37) and into equations of the dynamic balance (30), (31) results in the system of  equations to calculate unknown coefficients
equations to calculate unknown coefficients 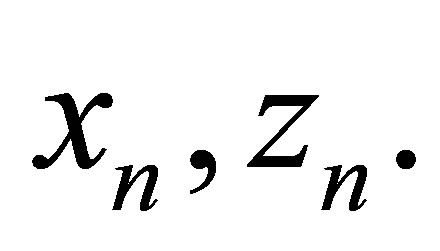 The characteristic equation for wave numbers
The characteristic equation for wave numbers 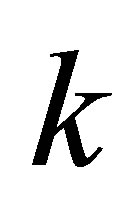 of elastic axisymmetrical waves in the transversely isotropic cylindrical shell we receive by expanding the determinant, which is equals zero. The axisymmetrical wave of the horizontal polarization (torsional wave) has only one component
of elastic axisymmetrical waves in the transversely isotropic cylindrical shell we receive by expanding the determinant, which is equals zero. The axisymmetrical wave of the horizontal polarization (torsional wave) has only one component 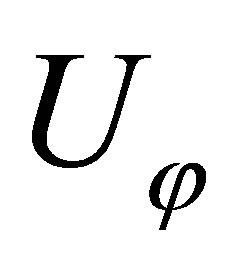 of the displacement vector
of the displacement vector 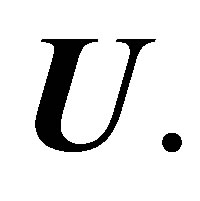 The problem in this case has the analytic solution. Components of strains
The problem in this case has the analytic solution. Components of strains 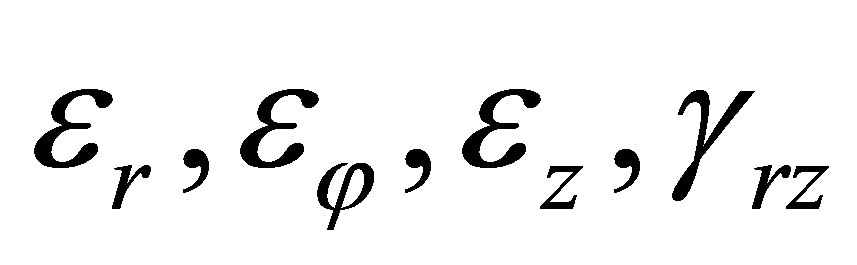 are equal to zero, but components of strains
are equal to zero, but components of strains 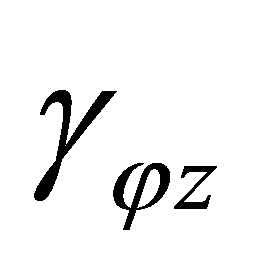 and
and 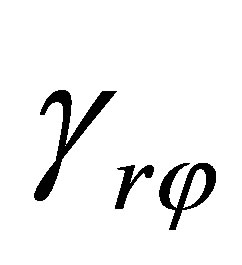 are equal to:
are equal to:
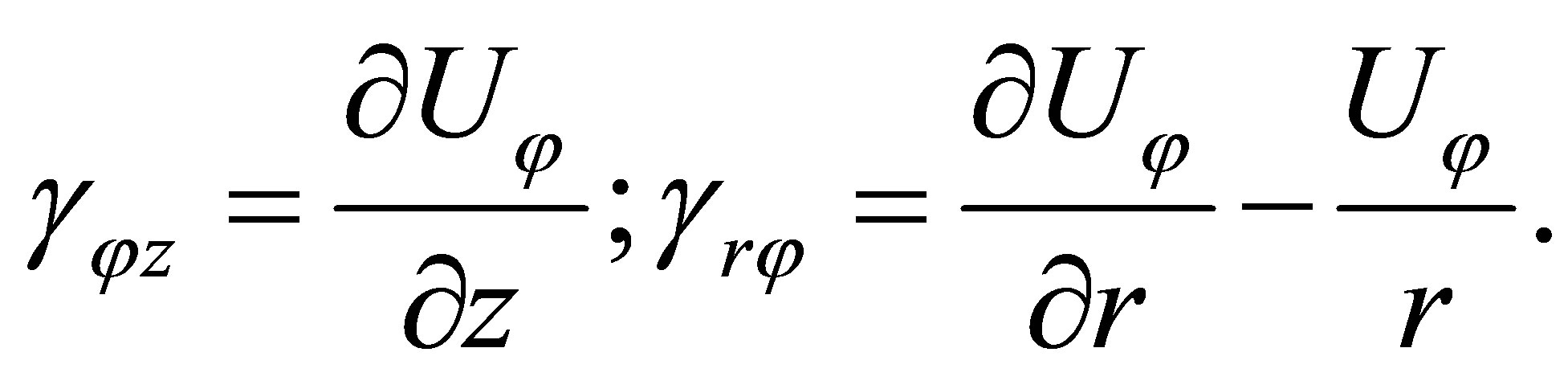
The equation of the dynamic balance has the following form:
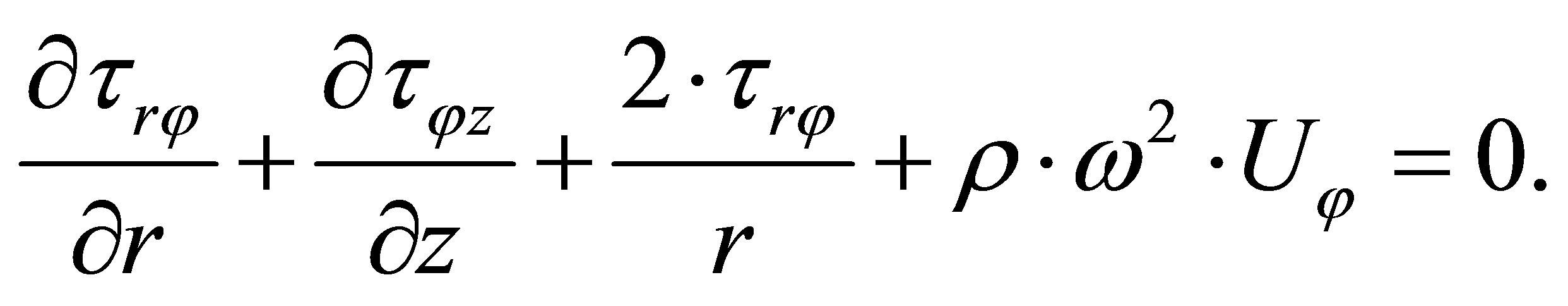 (38)
(38)
Used (2) and (3), we can describe (38) in the form:
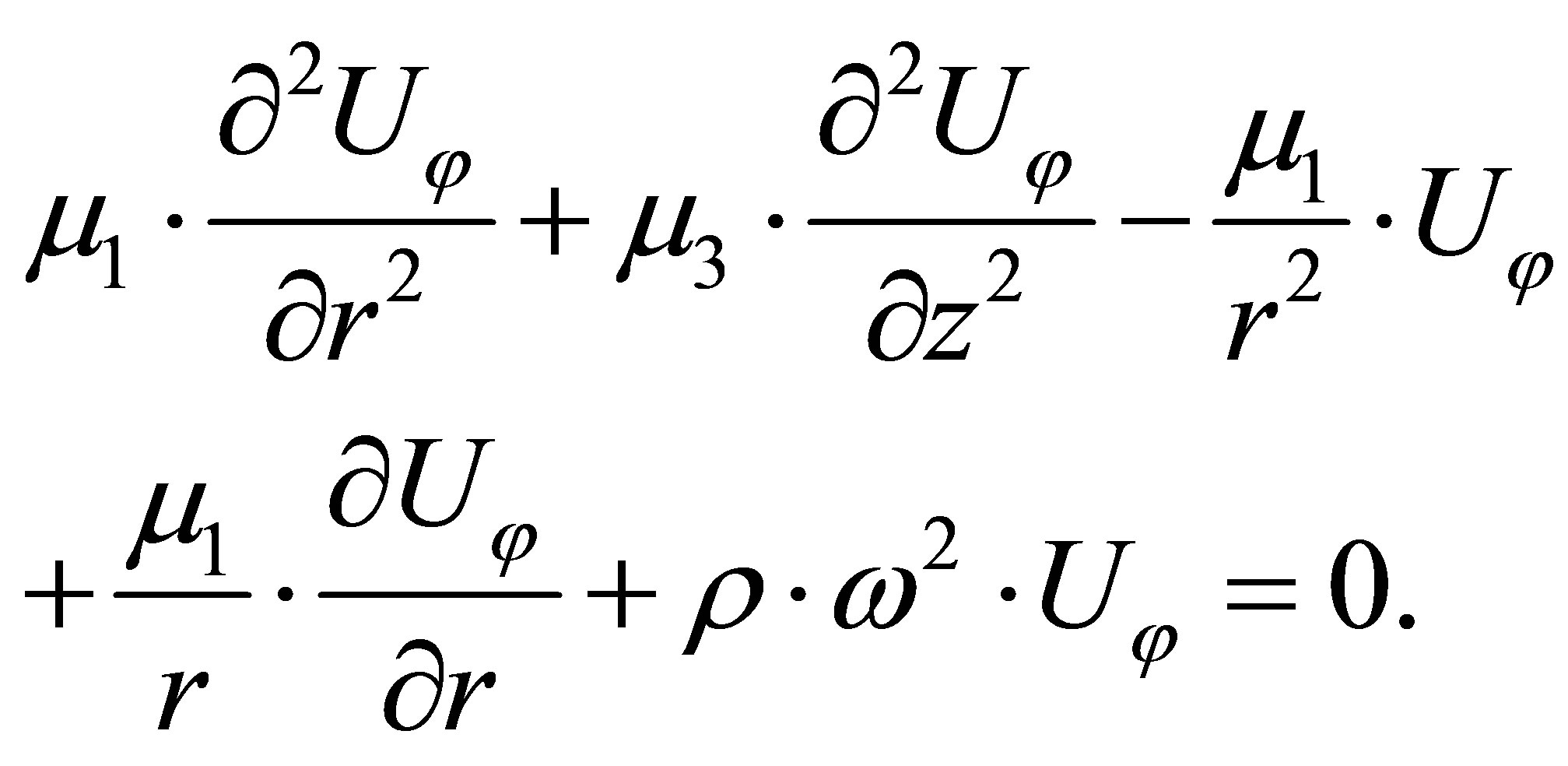 (39)
(39)
The component Uφ can be presented as:
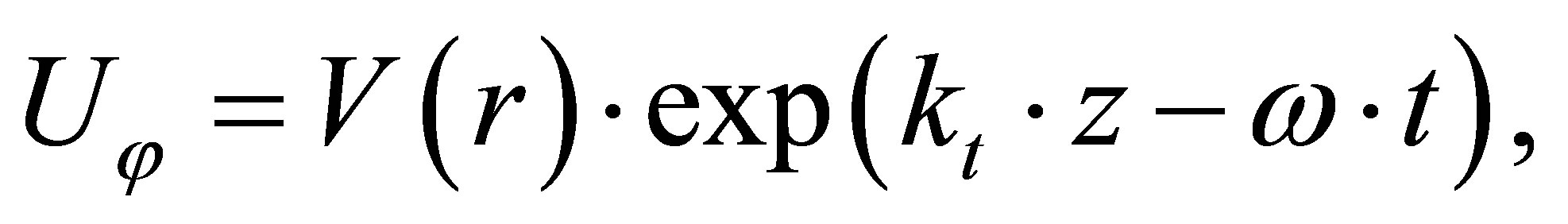 (40)
(40)
where 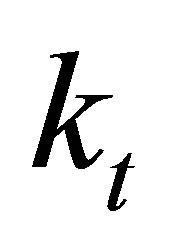 is the torsional wave number.
is the torsional wave number.
We substitute (40) in (39) and have:
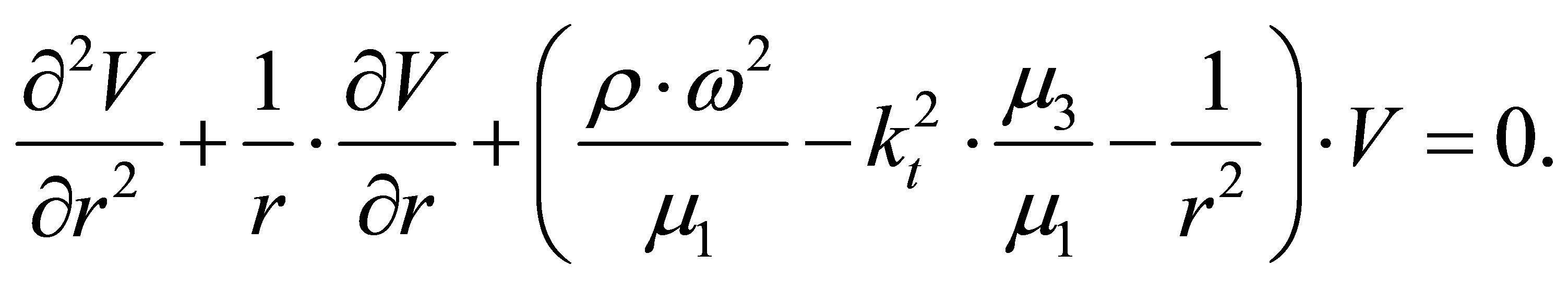 (41)
(41)
The Equation (41) is the Bessel’s equation for Bessel’s 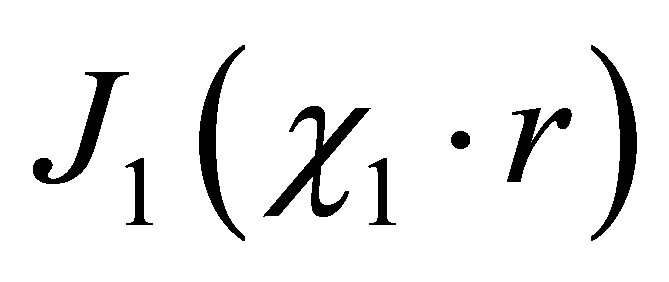 and Neiman
and Neiman 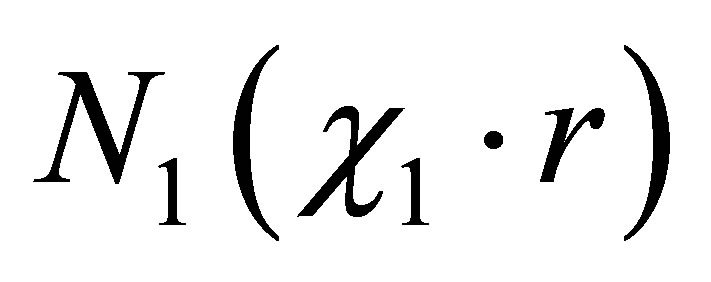 functions of the first order:
functions of the first order:
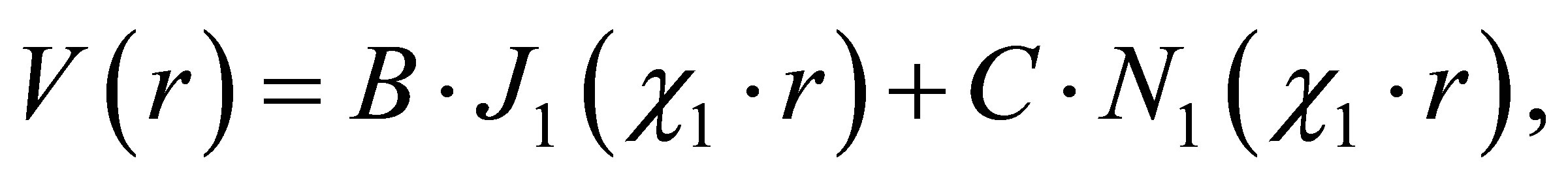 (42)
(42)
where  and
and 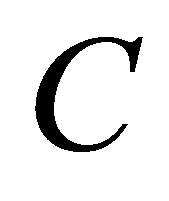 are arbitrary constants;
are arbitrary constants;
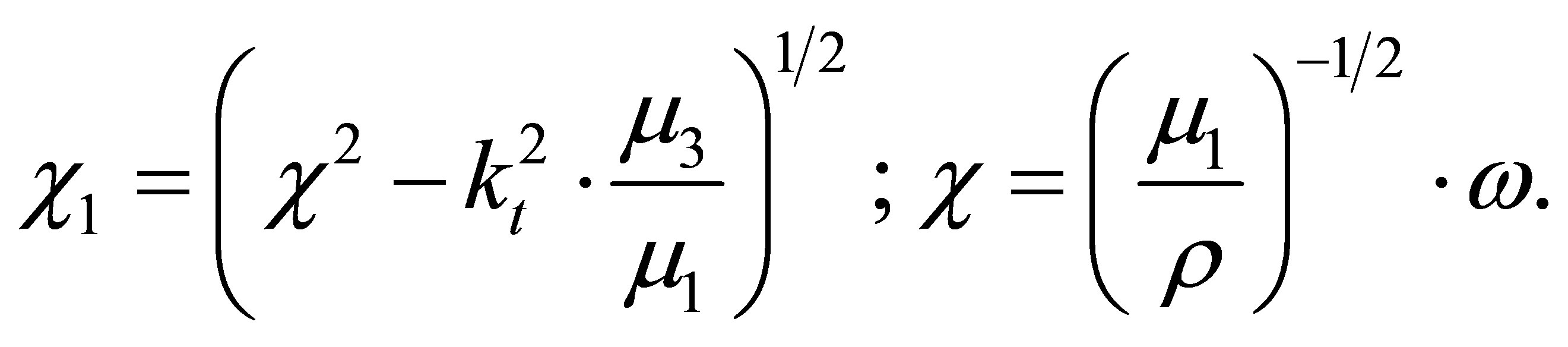
From the boundary condition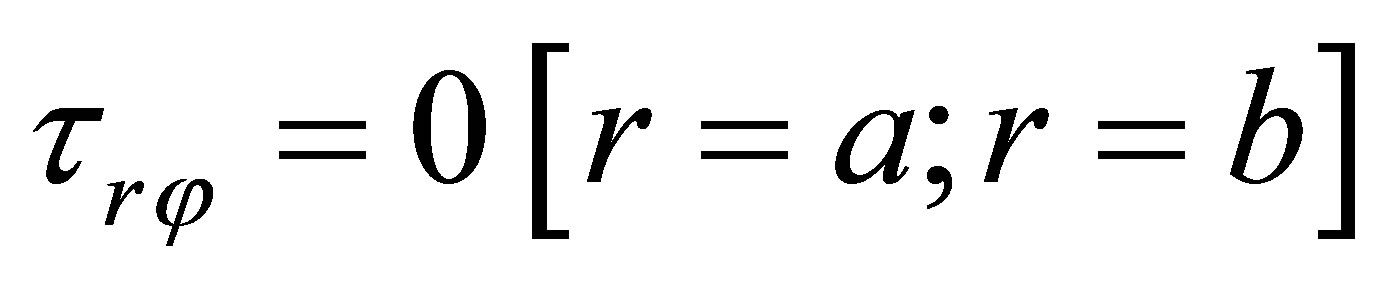 , we receive the characteristic equation for torsional wave numbers
, we receive the characteristic equation for torsional wave numbers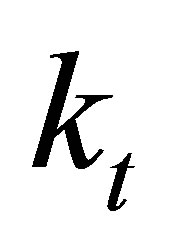 :
:
| |
where
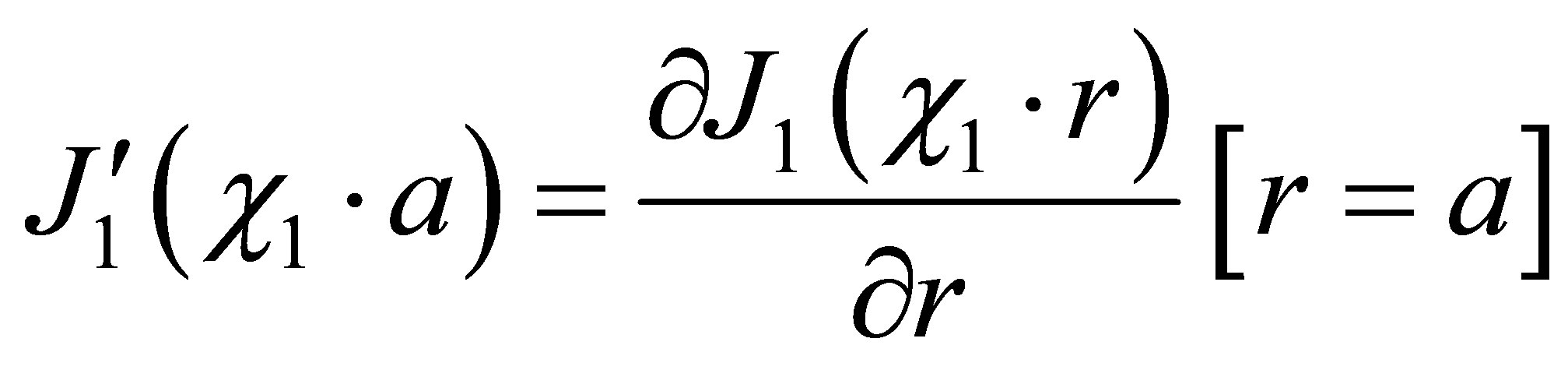 .
.
4. Conclusions
In the paper, we found the characteristic equation for wave numbers of elastic waves in thin transversely isotropic cylindrical shell with the help of the dynamic theory of the elasticity for the orthotropic medium and of the hypothesis of thin shells both for three—dimensional and axially symmetric problems.
5. Acknowledgments
The work was supported as part of research under State Contract no. P242 of April 21, 2010, within the Federal Target Program “Scientific and scientific—pedagogical personnel of innovative Russia for the 2009-2013”.
REFERENCES
- S. G. Lekhnitsky, “Theory of Elasticity of an Anisotropic Elastic Body,” M.: Science, 1977, p. 416.
- A. A. Kleshchev, “Against Phase Velocities of Elastic Waves in Thin Transversely Isotropic Cylindrical Shell,” Proceedings of the X session of the Russian Acoustical Society. M.: Geos, Vol. 1, 2000, pp. 206-210.
- A. A. Kleshchev, “Diffraction and propagation of waves in Elastic Mediums and Bodies,” Vlas, S.-Pb., 2002, p. 156.
- A. A. Kleshchev, “Diffraction, Radiation and Propagation of Elastic Waves,” Profprint, S.-Pb., 2006, p. 160.
- E. L. Shenderov, “Radiation and Scattering of Sound,” L.: Shipbuilding, 1989, p. 302.