ABSTRACT

It is demonstrated that the universally accepted system of gas-dynamic (hydrodynamic) equations is applicable only to homogeneous (isentropic) media and requires advancement to get applicable to non-homogeneous media. A generalized equation of gravitational wave for adiabatic and ideal media is obtained from advanced system. From this equation, in turn, is obtained an equation of acoustic wave, which is plane and different form the known equation in that the phase speed of the wave in the Earth atmosphere obviously depends on altitude, i.e. 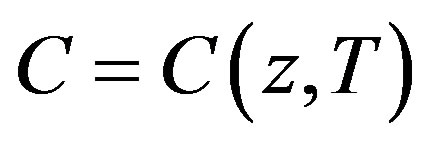instead of accepted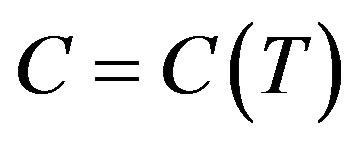. Thus, acoustic wave is a short-period gravitational wave in which gravitational effects are revealed at altitudes m, which leads to amplification of refraction of sound. The sphere of applicability of the equation is determined and it is demonstrated that it is true only up to the upper boundary of the troposphere (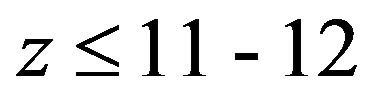km.) above which anomalous processes develop in the atmosphere.

1. Introduction

In the paper [1] it was shown that the expression of adiabatic speed of sound, 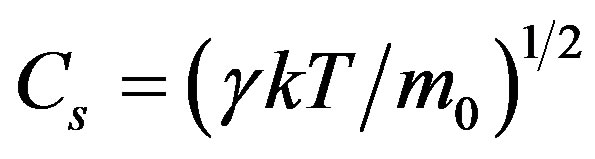with the help of which the speed of sound is currently determined in lower as well as upper layers of the atmosphere, is applicable only up to the altitudes z ≤ 10³ m. Above this altitude obvious dependence of the sound speed on coordinates z is revealed along which the atmosphere is non-homogeneous as a result of influence of gravitational field of the Earth. Revelation of the factor of gravitational filed became possible due to the fact that in the equation of the state of the atmosphere, considered to be an ideal gas, entropy s is taken into consideration and is written in the form 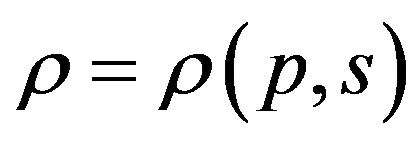instead of generally accepted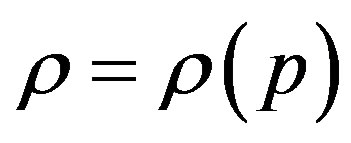, which is true only for isotropic media and is not applied to the Earth atmosphere. Such approach enabled to determine that along with adiabatic mechanism of generation of sound wave, there exists an isobaric one and exactly this mechanism leads to dependence of the speed of sound on altitude z or on density, which is the same. The true value of the square of sound speed which is deduced from the squares of adiabatic and isobaric speeds of sound 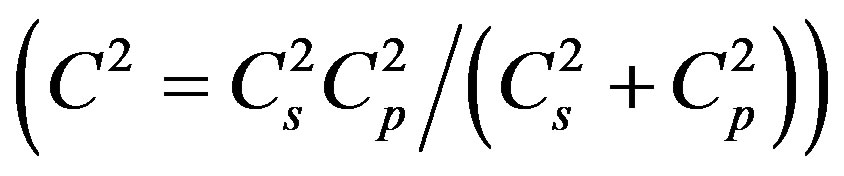is obtained from equation of the state of the medium and is defined as the coefficient connecting perturbation pressure and density.

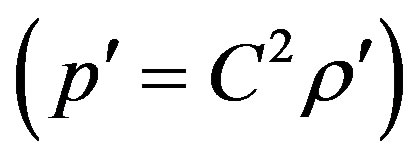The present paper demonstrates that the known system of gas-dynamic (hydrodynamic) equations is also satisfactory only for homogeneous (isotropic) media and requires advancement to get feasible for non-homogeneous media. Thereafter, the advanced system of equations is reduced to the generalized equation of gas-dynamic (hydrodynamic) waves in non-homogeneous medium. Application of this equation to perturbations of the Earth atmosphere with frequency bandwidth corresponding to the sound frequencies of range (10 - 104) Hz, shows that the equation of sound wave in the Earth atmosphere is in the form of plane wave with the only difference that the square of sound speed in it coincides with the value determined in the paper [1], i.e., in contrast to currently accepted.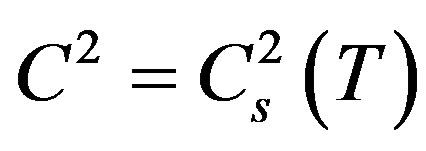

2. Advanced System of Gas-Dynamic (Hydrodynamic) Equations

Motion of frictionless liquid (or gas) in the gravitational field of the Earth is described by the equation of Euler:

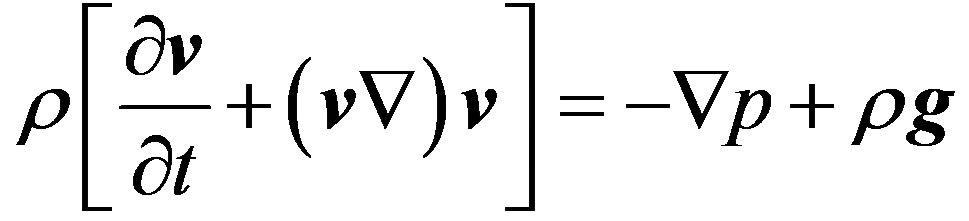(1.1)

which is solved in conjunction with the equations of continuity of mass

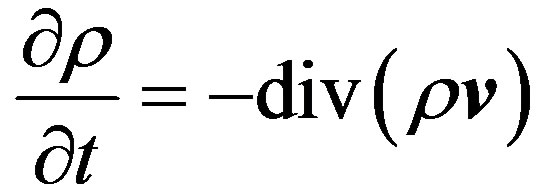(1.2)

and adiabatic equation

(1.3)

The Equation (1.2) determines change of density liquid particle in given volume V and says that it equals to difference of mass flows incoming and outgoing through the surface limiting such volume [2]. However, change of density may occur at the cost of either change of substance mass in constant volume or change of volume of constant mass of substance. Indeed:

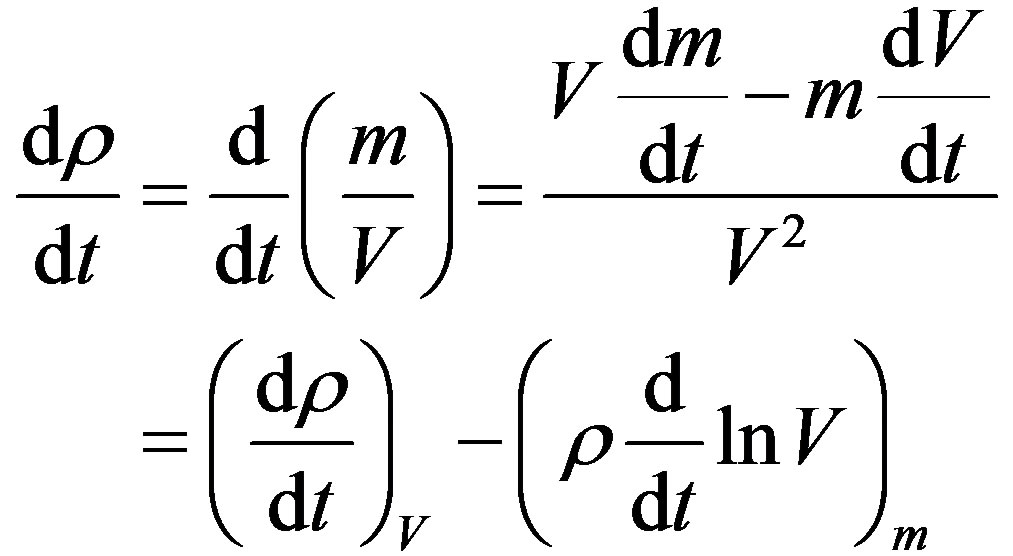(1.4)

Assuming in second summand of the right part of the Equation (1.4) m = 1 i.e.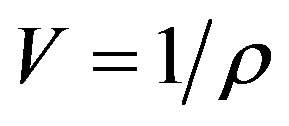, we obtain:

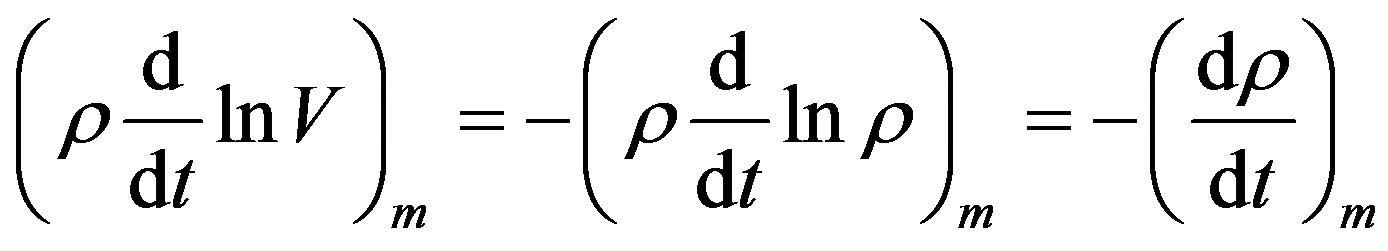
and finally from (1.4) we find out

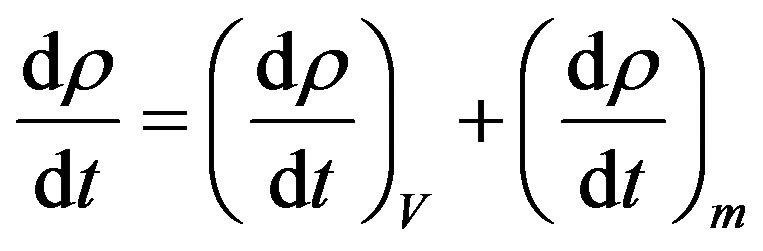(1.5)

Hence, complete change of density consists of two parts, the first of which is determined by the Equation (1.2), i.e.

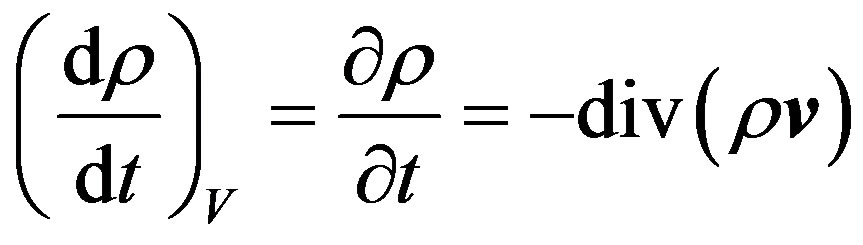(1.6)

The second part describes change of density of the substance of constant mass as a result of change of volume which may occur only due to change of temperature which, in turn, in the absence of heat source, is possible only under change of entropy.

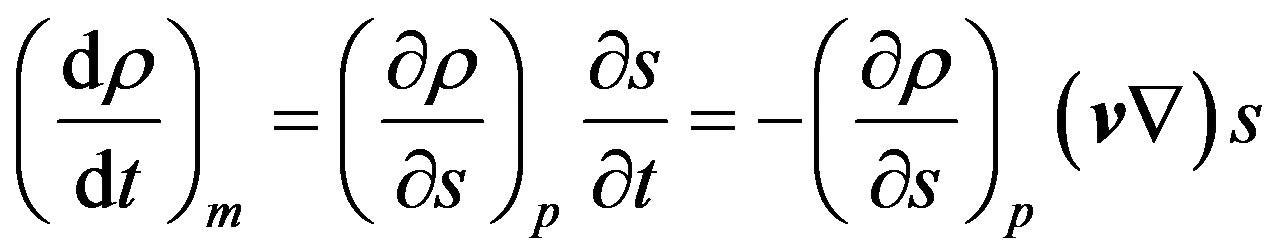(1.7)

Adiabatic Equation (1.3) is used here. For homogeneous (isotropic) medium 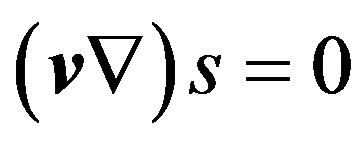and (1.5)-(1.7) makes obvious that change of density of liquid particle is indeed determined under the Equation (1.2). For non-homogeneous medium it can be written

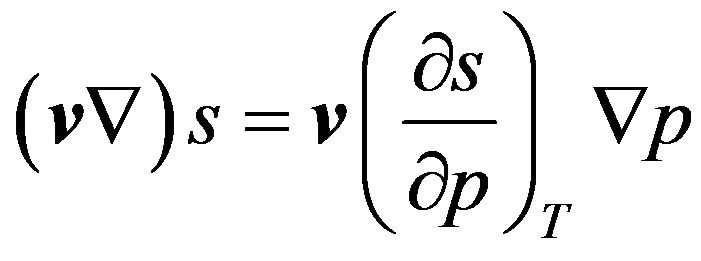(1.8)

and then, proceeding from (1.5)-(1.8) the equation of continuity of mass in non-homogeneous media will have the form of:

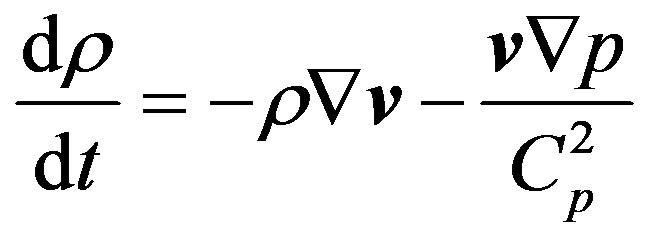(1.9)

where

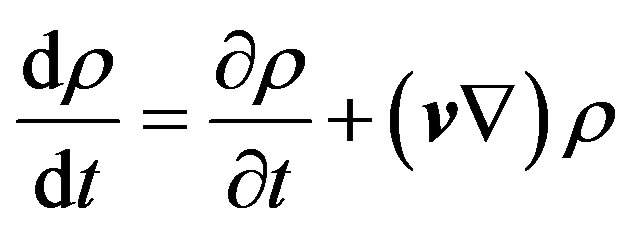(1.10)

and the value 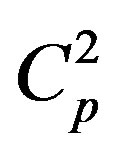the dimension of speed square and equals to [1]

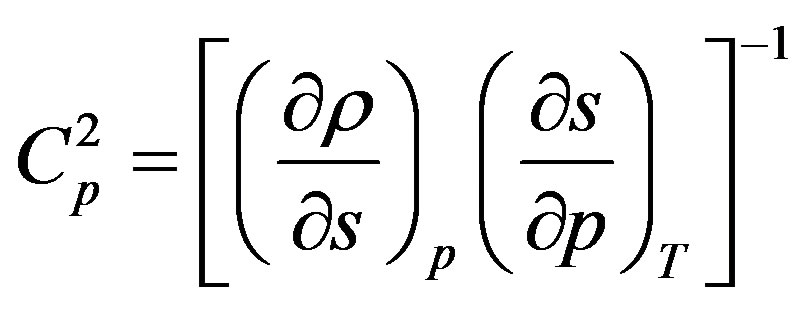(1.11)

Thus, (1.9)-(1.11) make apparent that in non-homogeneous media, when they are incompressible 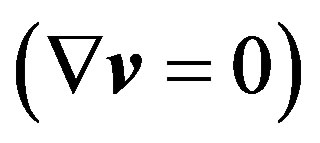density is all the same changed in the circumstance of entropy perturbance. In light of the aforementioned the system of equations of gas-dynamic (hydrodynamic) for non-homogeneous media should have the form:

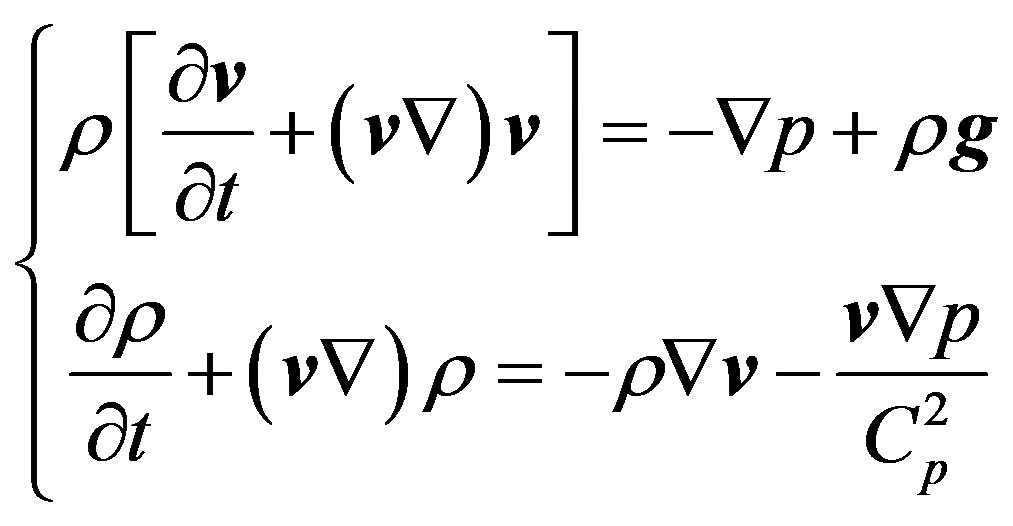(1.12)

3. Generalized Equation of Gravitational Waves

At wave motion v and 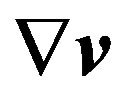are considered small quantities and pressure p and density 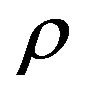are represented in the form of the sum of their stationary 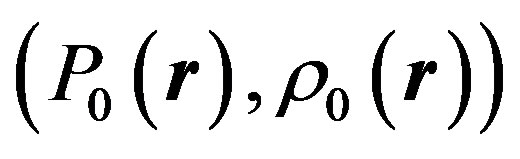and perturbed 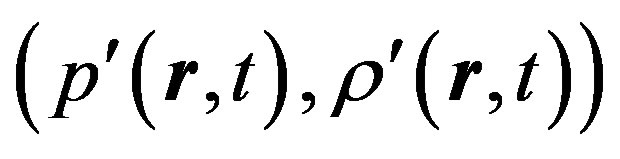values, after which the linearized system of Equation (1.12) takes the form

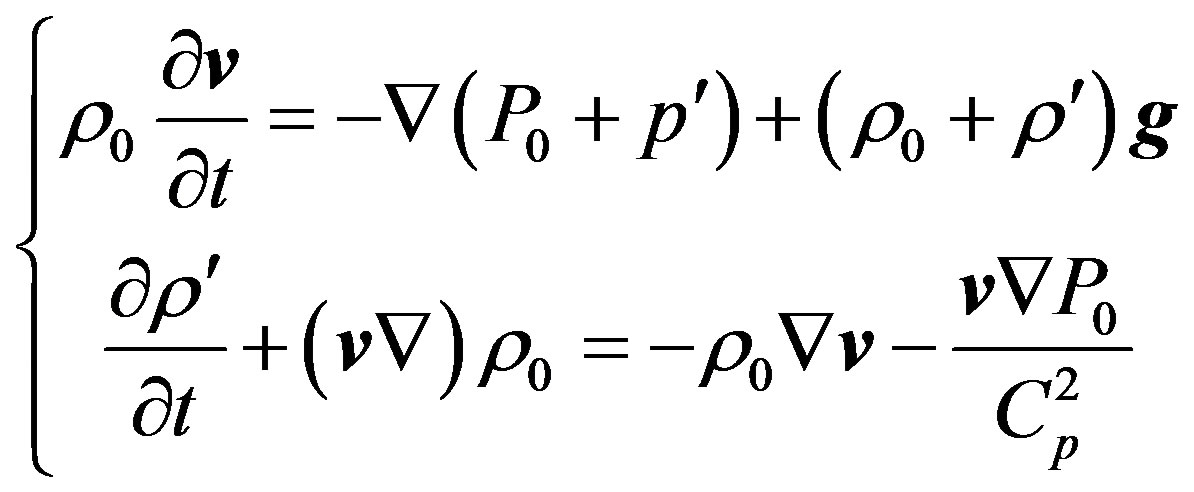(2.1)

By using the equation of equilibrium of medium in gravitational field 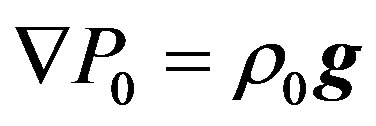and equation of the state of medium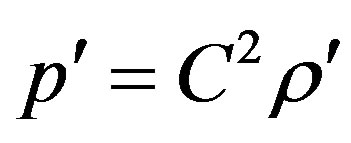, where 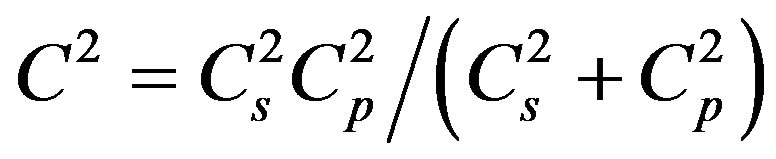(see [1]), the equation system (2.1) can easily be reduced to the equation of gas-dynamic (hydrodynamic) waves in gravitational field of the Earth.

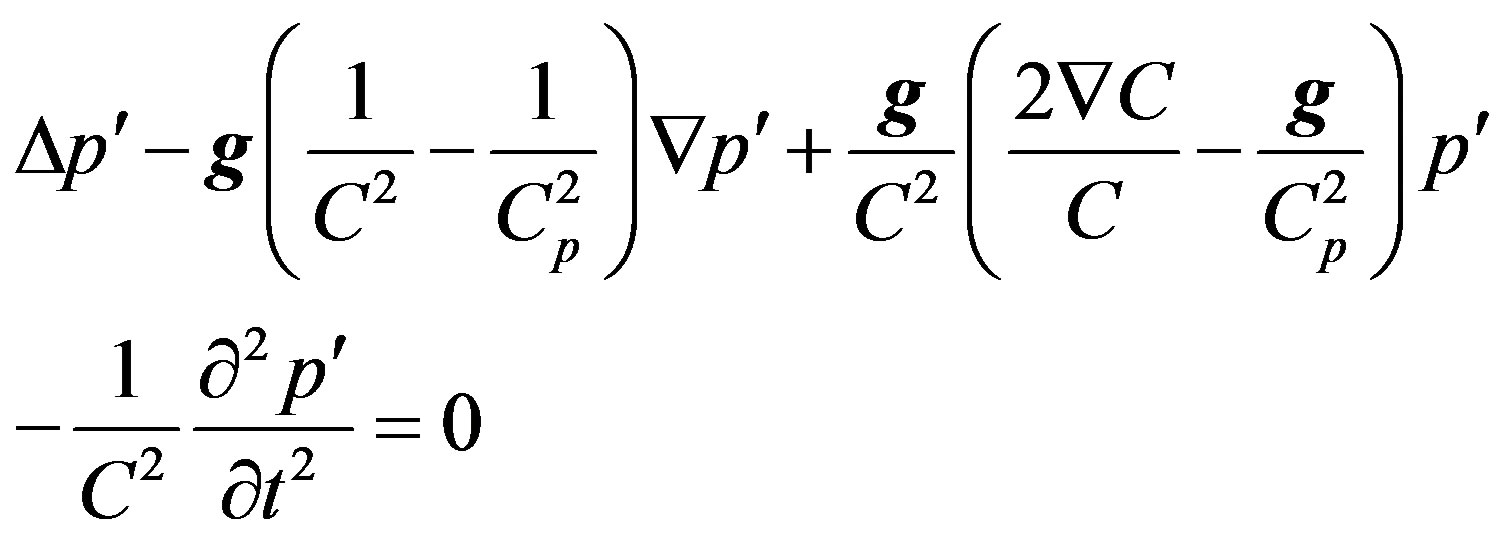(2.2)

The Equation (2.2) may be called the generalized equation of gravitational waves in ideal (nondissipative) and adiabatic media. In particular case, under corresponding values of coefficients, the equation of sound wave in the Earth atmosphere can be obtained from this equation. Consequently, the sound wave is a short period (high-frequency) gravitational wave (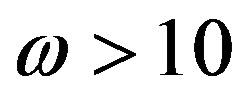Hz) and the current opinion that the gravitational field has no influence on generation and propagation of sound wave is incorrect. The first attempts of correct derivation of the equation of gravitational fields were taken in the works [3] and [4], however the equation of continuity of mass was used in the form of (1.2) and therefore their results differ from the Equation (2.2).

4. Equation of Sound Wave in the Earth Atmosphere

It was mentioned above that the sound speed in the whole atmosphere is defined by formula

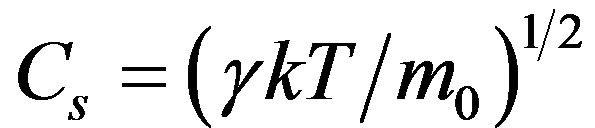
which does not take into consideration the effect of gravitational field. In actual practice the sound speed in the Earth atmosphere should be identified from Equation (2.2) and for this purpose it is necessary to determine the sphere of its application. Let’s first call C² a square of a certain speed which is reduced from squares of certain speeds 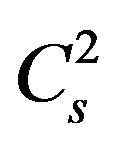and, where (see [1])

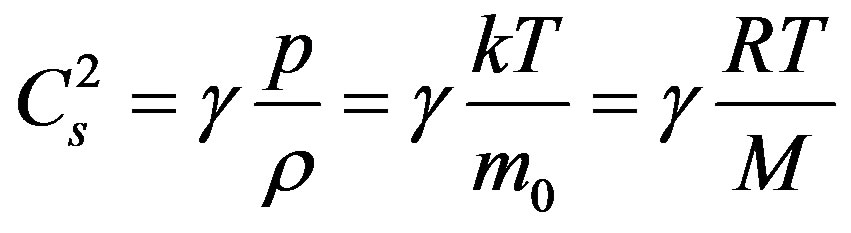(3.1)

and

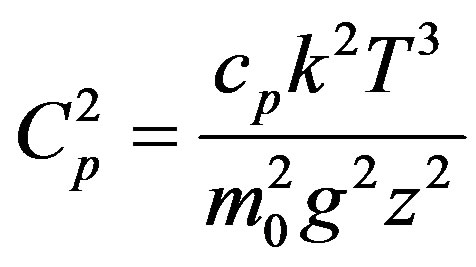(3.2)

Then, for C² we will have

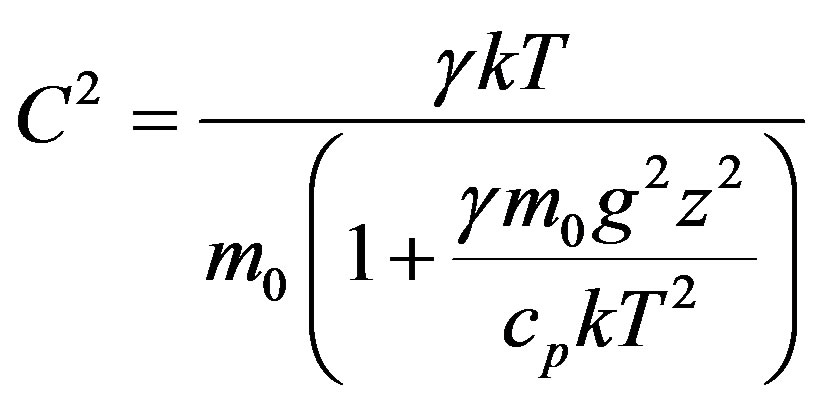(3.3)

Here R = 8.314 J/(mol·K)—gas constant, m₀ = 4.81 × 10^–26 kg—mass of one molecular of air and m = 29 × 10^–3 kg/mole—mass of one mole of air, while the adiabatic index 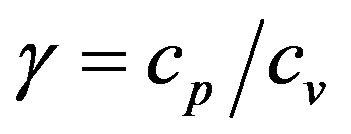= 1.4 is the relation of heat capacity of air under constant pressure and volume. Expressions (3.1) and (3.2) imply that the Earth atmosphere represents the ideal gas 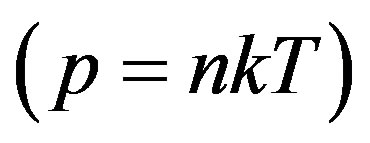and dependence of density on altitude is described by Laplace barometric formula

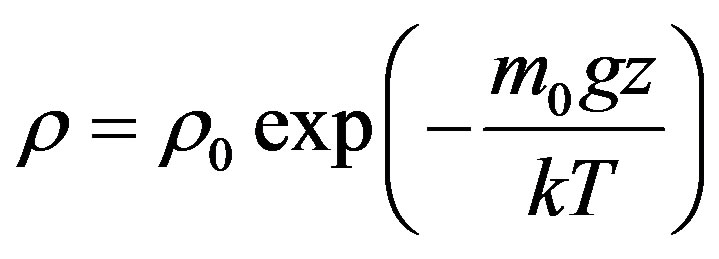(3.4)

However, as it appears from experimental data [5] at the altitude z = 7.5 km, where air density is calculated according to the formula (3.4) drops e times, ratio error between calculated and experimental values of density equals to 23% and at the altitude z = 11 km it constitutes 40%, moreover the experimental data exceed the calculated ones. At the altitude z = 35 km they equalize and then error again increases and at the altitude z = 85 km reaches 95%. It follows that the formula (3.4) works poorly in the Earth atmosphere, especially in the upper part of it. Besides, as it is apparent from the chart of dependence of temperature on altitude ([1,5,6]), constructed on the basis of experimental measurements, in the interval of altitudes from z = 0 to z = 12 km, temperature drops monotonously according to the linear law and approximately according to the law 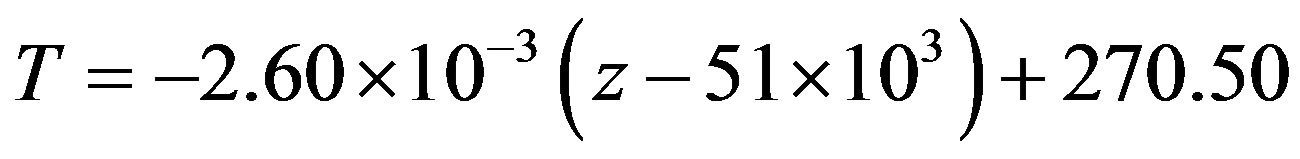in interval of altitudes from z = 51 km to z = 85 km. In the intermediate interval (12 - 51 km) the temperature is either constant or increases, which allows to assume that either heat exchange or dissipative processes occur there. In the first case the medium is nonadiabatic while in the second case it is not ideal gas. Thus, application of formula (2.2) to the whole atmosphere would be incorrect. We assume that it describes in good approximation wave processes in the Erath atmosphere only in the interval of altitudes from z = 0 to z = 11 - 12 km, i.e. in the troposphere, where temperature drop strictly obeys the linear law and in which ratio error between experimental and calculated value of density is insignificant. As shown in [1] the upper boundary of this interval coincides with the altitude at which 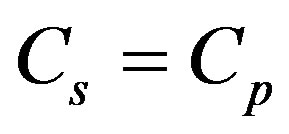and is defined by the expression

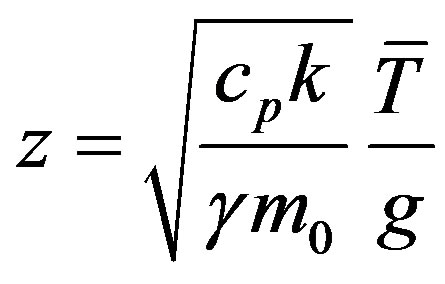=11.6 km(3.5)

where C_p = 10³ J/kg K and 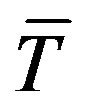= 252.4 K is average value of temperature. We are not ready to discuss here the reasons of this coincidence however we assume that it has a deep physical meaning.

Coefficient estimation at p' in Equation (2.2) shows that in the specified interval it changes within the range 10^–6 - 10^–7 and thus this summand may not be considered. Consequently, wave processes in the troposphere (0 - 12 km) are described by equation

(3.6)

Let’s consider the Equation (3.6) for the waves spreading in horizontal 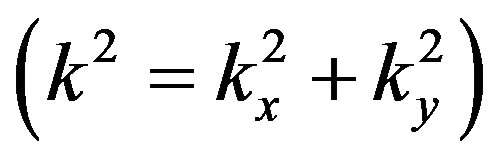and vertical directions. In the first case p' is represented in the form

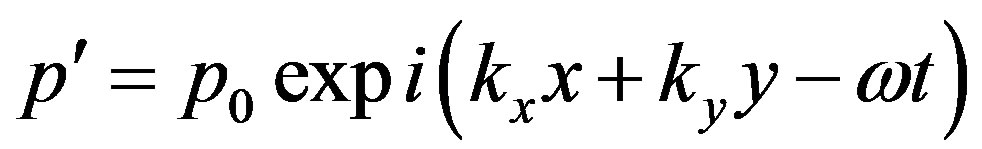(3.7)

after which and the Equation (3.6) transfers into equation of plane wave

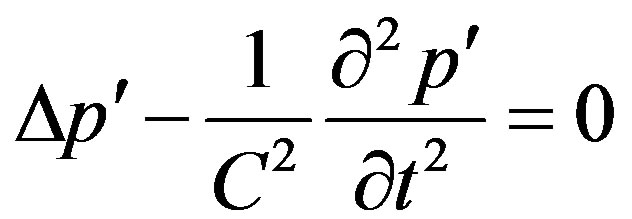(3.8)

in which

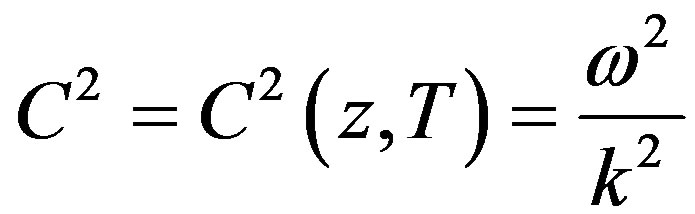(3.9)

is determined according to the formula (3.3) and has the meaning of the square of phase speed of the wave, which is called sound or acoustic wave. Hence, speeds determined according to the formulas (3.1) and (3.2) can also be called adiabatic and isobaric speeds of sound.

For waves spreading in vertical direction (along the axis z) the Equation (3.6) has to be solved by method of geometrical optics, since in this direction the atmosphere is non-homogeneous as a result of influence of gravitational field. Following this procedure [7] pressure perturbation will be presented in a form

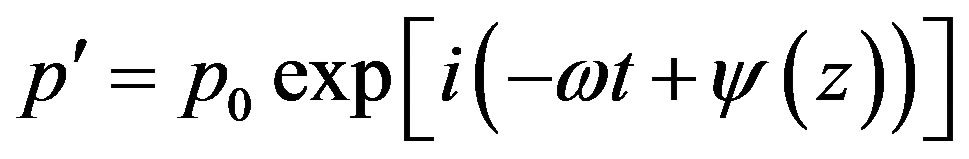(3.10)

where is a certain dimensionless function which satisfy the equation

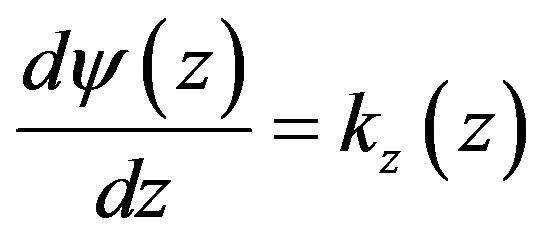(3.11)

Then from Equation (3.6) we will get

(3.12)

The prime mark is herein taken to mean derivative with respect to z. By denoting the upper boundary of the troposphere through z₀, which is determined by formula (3.5) it will be easy to demonstrate that

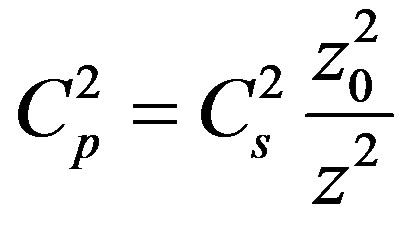(3.13)

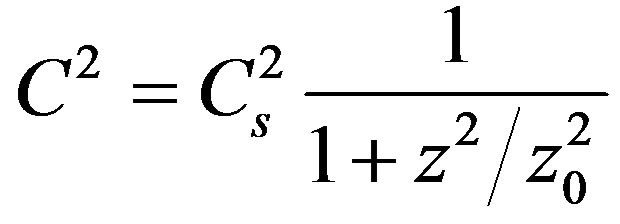(3.14)

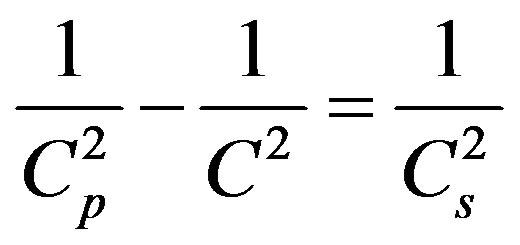(3.15)

Consequently, the Equation (3.12) may be written as

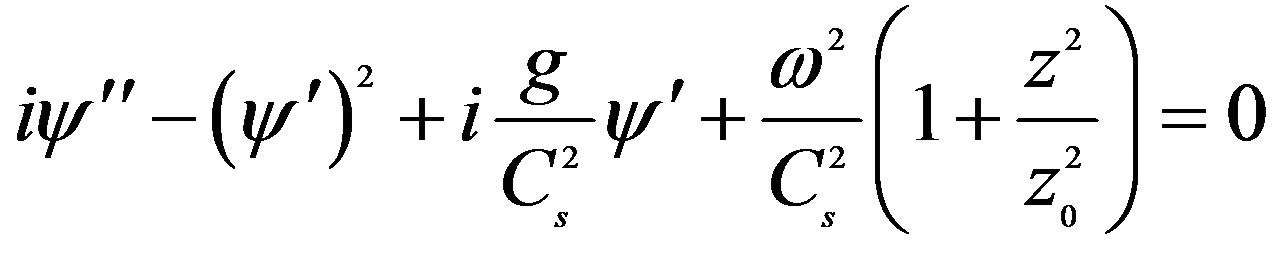(3.16)

Let’s expand 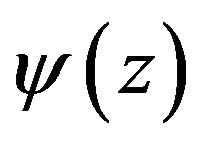along small parameter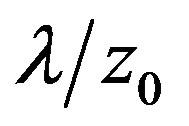, where λ is the wave length and z₀ is the size of non-homogeneity of medium

(3.17)

and solve the Equation (3.16) in null approximation for which purpose we set 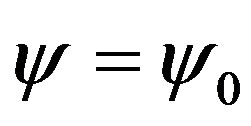and ignore the second derivative and thereafter we will obtain

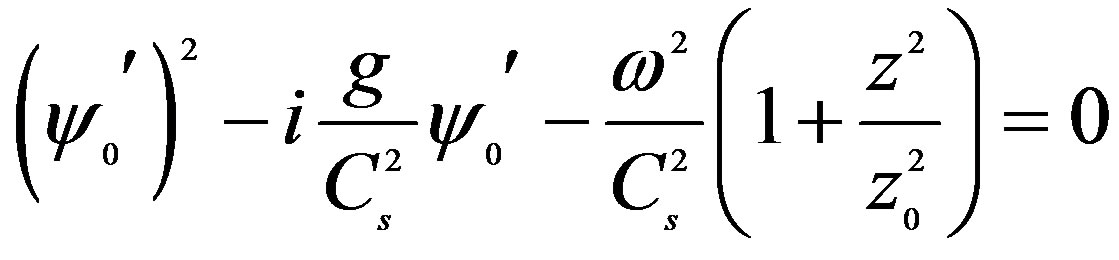(3.18)

from which for 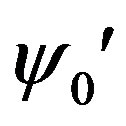we’ll find

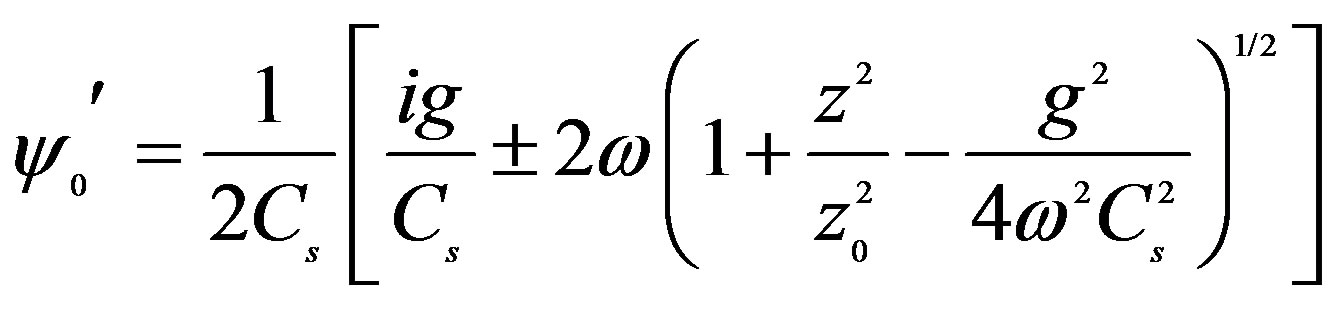(3.19)

From (3.19) it is seen that for propagation of sound along axis z the expression under the radical must be nonnegative, i.e. it is necessary to fulfill the condition

(3.20)

The function 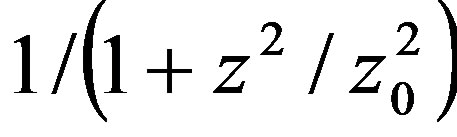is close to unit in the whole interval of change of z and therefore from (3.20) it follows that

Hz        (3.21)

As we see sound propagation condition is fulfilled with big reserve and for sound frequencies (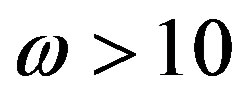Hz), after neglect of the terms above the first order of smallness (which is equivalent to neglect of the second summand in Equation (2.18)) the Equation (3.19) will result in

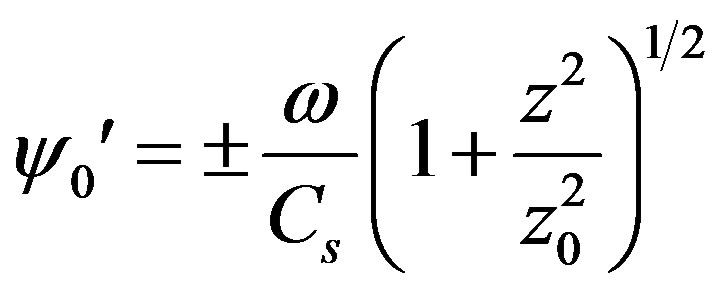(3.22)

Thus, sound wave spreading in vertical direction is also flat.

Let’s now find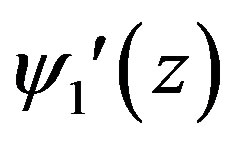, and with this purpose let’s insert 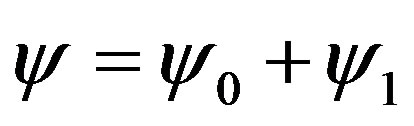in (3.16). Having ignored the small quantity of the second order and taken into consideration the Equation (3.18) we will obtain

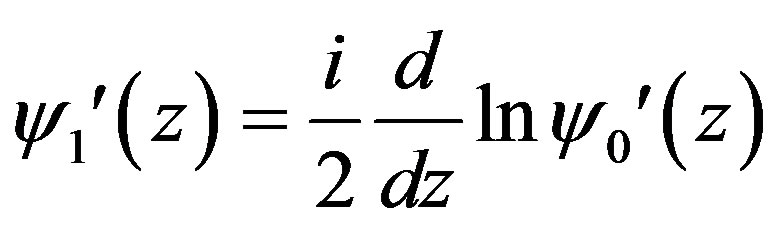(3.23)

From (3.23) it is obvious that in (3.22) the sign “+” should be taken. Suppose the sound source is in point 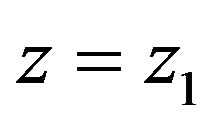(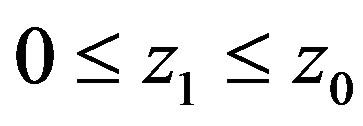) and assume that in the stated interval temperature loosely depends on altitude, set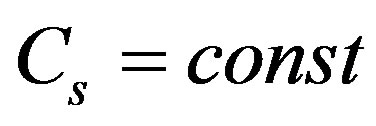. Then from (3.22) and (3.23) for 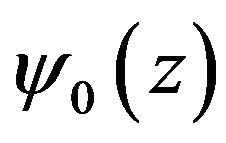and respectively we will obtain

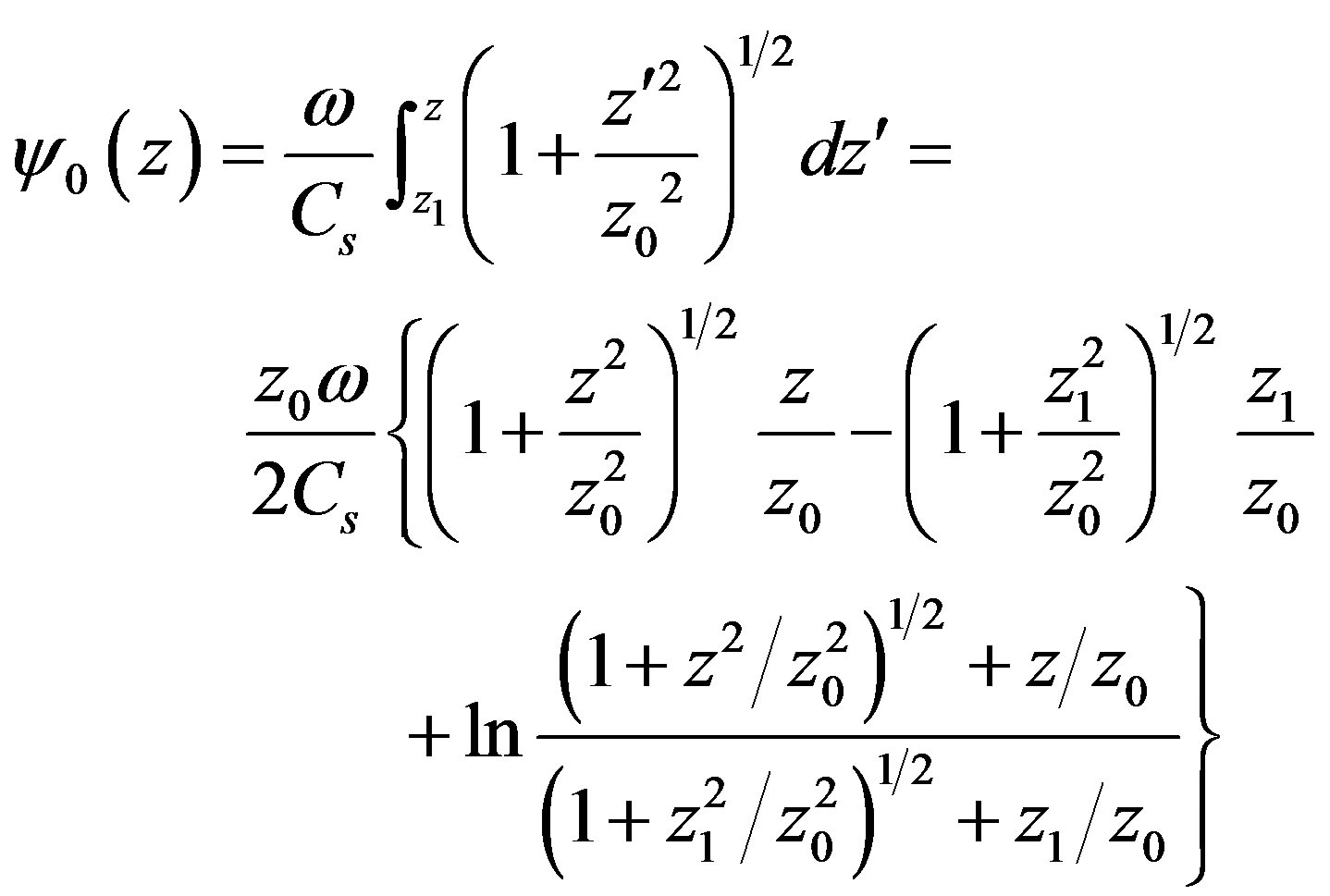(3.24)

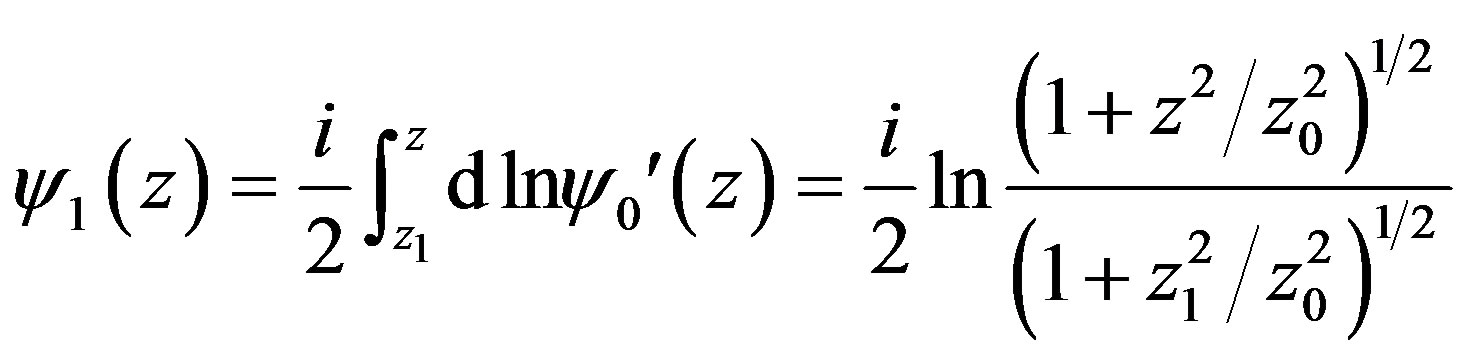(3.25)

From (3.10), (3.24) and (3.25) for pressure perturbation in first approximation we will have

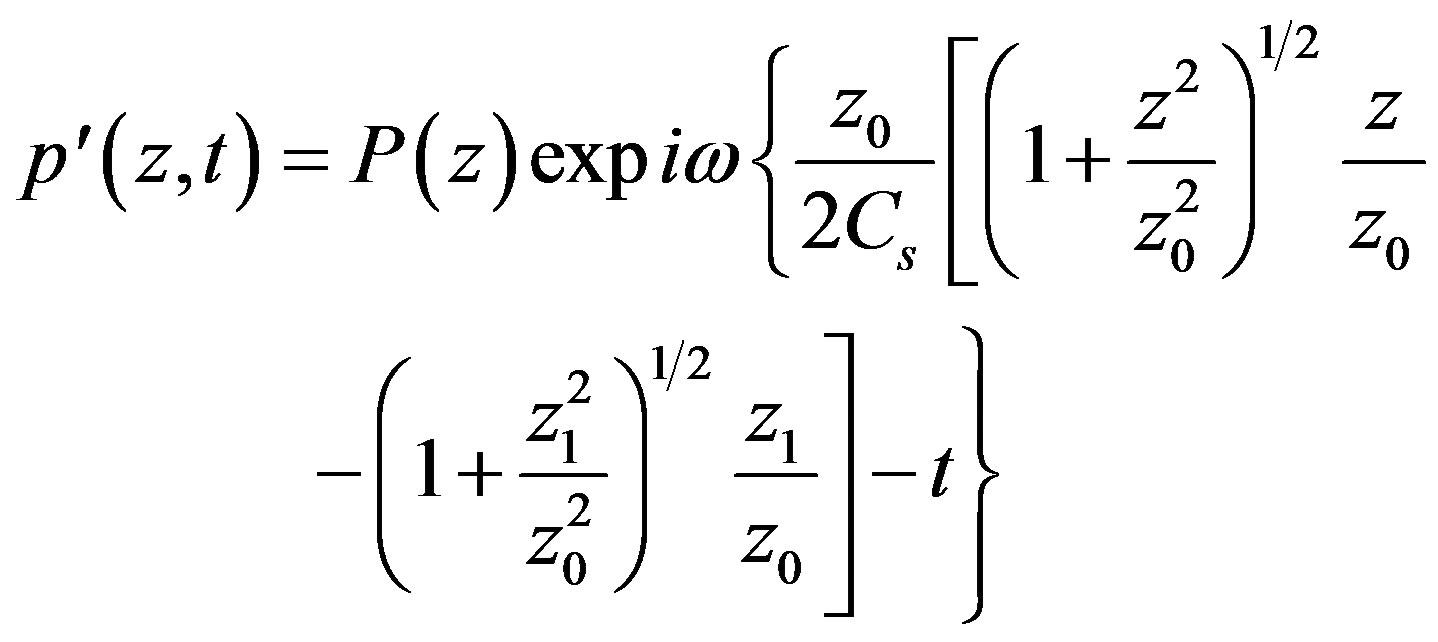(3.26)

where

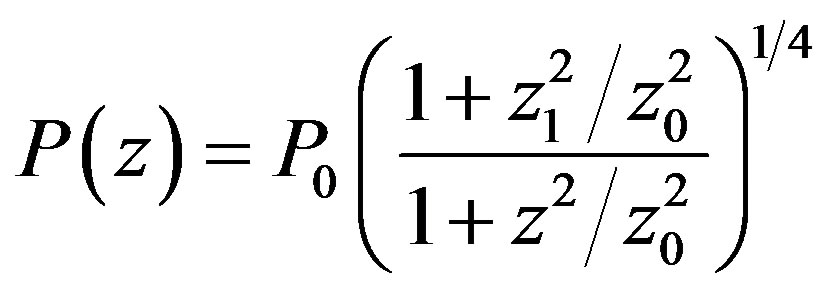(3.27)

From (3.27) we see that when the sound is propagated from the bottom to the top the wave amplitude drops while when it is propagated from the top to the bottom it increases. Thus, for instance if the sound source is at sea level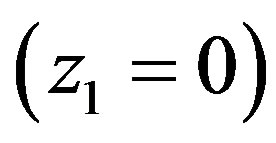, then by reaching altitude z = z₀, wave amplitude.

Let’s now find, which by convention is 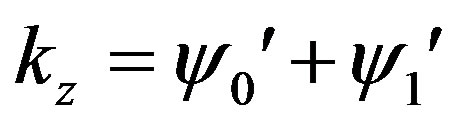and using expressions (3.22) and (3.23) we will find

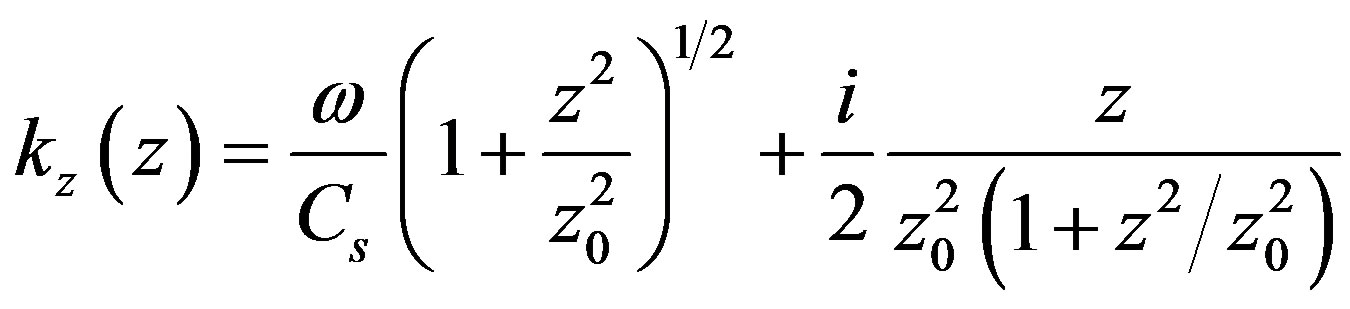(3.28)

Module of imaginary component k_z achieves largest extremum in the point z = z₀ and equals to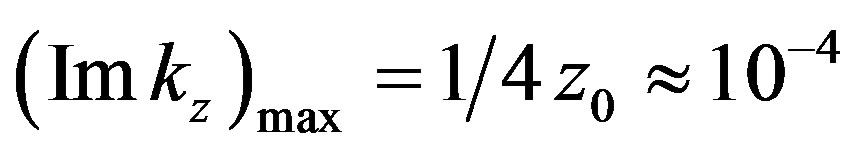, which allows to ignore it as compared to the real part and finally we will get

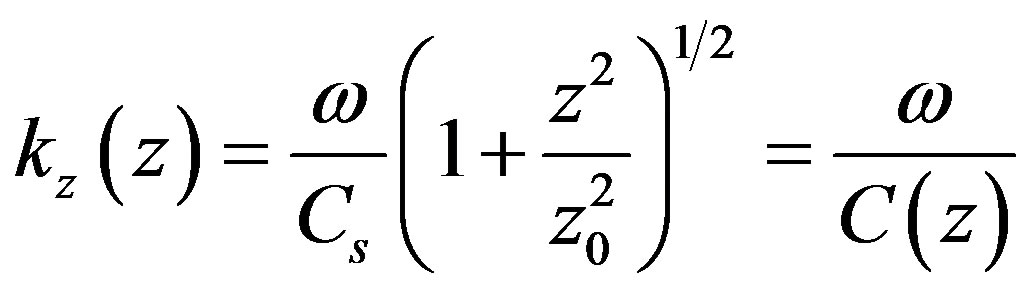(3.29)

As we see, the sound wave equation in any direction has the form of the equation of plane wave and the wave number in vertical direction is analytically expressed by the formula similar to the horizontal direction. However, there is difference between them. In the second case the wave number at the stated altitude has a constant value while in the first case it increases when sound is propagated from the bottom to the top and decreases in case of top-to-bottom propagation. Such behavior of 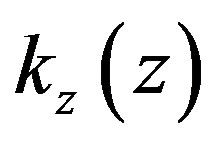serves as a reason for the phenomenon know as “sound refraction” which is that in the course of propagation of the sound wave the direction of wave vector changes to the side of decrease of the sound speed. In the current theory this phenomenon is explained by gradient along the axis z of adiabatic speed of sound C_s which is conditioned by its dependence on temperature T, which in its turn depends on z according to the aforementioned law. Adhering to our theory, gravitational field of the Earth also contributes to sound refraction which is expressed by emergence of facient 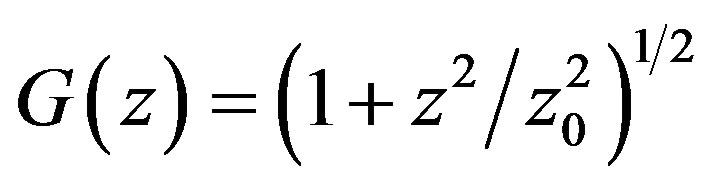in (3.29). For assessment of this contribution it is necessary to calculate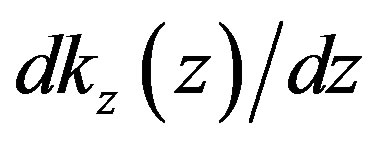, which equals to

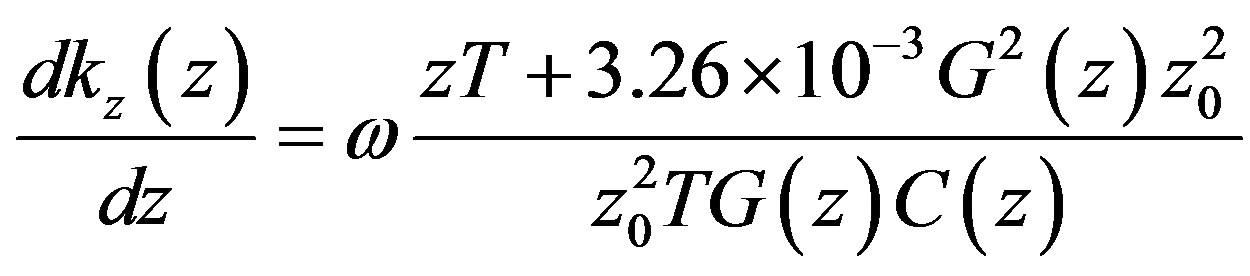(3.30)

Effect of gravitational filed takes into consideration the first term in numerator (3.30), influence of which becomes determining when

m(3.31)

Here we assume that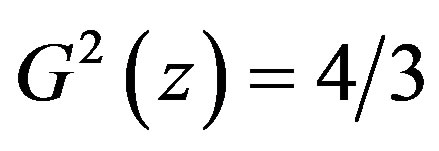и T = 252.4 K are the average values of these volumes. Apparently this is the altitude up to which the sound can be considered adiabatic and above which influence of gravitational filed cannot be ignored.

5. Conclusions

The most important result of the work is generalization of the equation of continuity of mass for non-homogeneous media after which it acquires clearer and finished physical meaning. According to the existing notion change of density in incompressible media is impossible since it is impossible to change the mass of liquid particle of stated volume. Developed equation of continuity of mass (1.9) does not contradict to the universally accepted definition of incompressibility of medium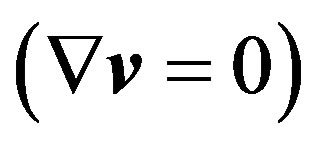, however it demonstrates that for such media change of density is all the same possible at the cost of change of the volume of selected liquid particle as a result of entropy oscillation which certainly occurs in the process of mechanical oscillations in non-homogeneous media.

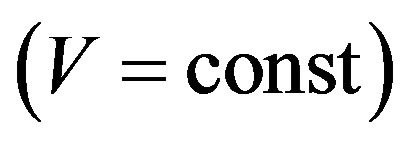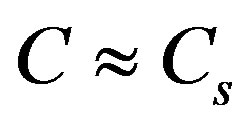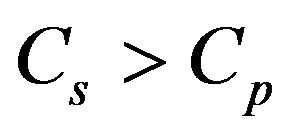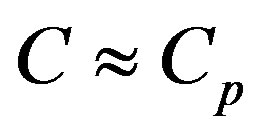Thus there exist two mechanisms of perturbation of density: adiabatic and isobaric. When the first mechanism prevails and, i.e. the medium is compressible. In case of prevalence of the second mechanism and, i.e. the medium is incompressible. This result has great significance, since in incompressible approximation which is often applied in solving applied problems, the equation of state of medium is often present in the system of equations and in its absence the system is unable to describe the real physical process adequately. Besides, in the work it is demonstrated that the sound wave is plane the equation of which is obtained from the generalized equation of gravitational waves on the assumption of adiabaticity and ideality of the medium. Consequently, established inference that acoustic wave is not gravitational is erroneous. Gravitational effects appear at altitudes z > 2.3 × 10³ m which in the first place is expressed in growth of sound refraction. This is the very reason due to which sound so far has been considered adiabatic in the whole atmosphere. Our calculations also demonstrate that they are true up to the upper boundary of the troposphere above which anomalous processes occur in the atmosphere.

Preceding from the aforementioned it is safe to say that the new theory of sound waves suggested by us will trigger qualitatively new researches in gas dynamics as well as in hydrodynamics.

The author expresses profound gratitude to Professor A. Rukhadze for useful advice and recommendations.

REFERENCES