Open Journal of Acoustics
Vol. 2 No. 2 (2012) , Article ID: 20453 , 6 pages DOI:10.4236/oja.2012.22009
Speed of Sound in Atmosphere of the Earth
Ilia Vekua Sukhumi Institute of Physics and Technology, Tbilisi, Georgia
Email: sipt@sipt org.ge, v.kirtskhalia@gmail.com
Received March 5, 2012; revised April 3, 2012; accepted April 10, 2012
Keywords: Speed of Sound; Atmosphere; Compressibility; Incompressibility
ABSTRACT
It is demonstrated that contemporary conception on adiabaticity of sound in the Earth atmosphere is fair in sufficient approximation only for altitudes z ≤ 103 m. At higher altitudes adiabaticity of sound is violated and essential dependence of its speed on altitude is revealed which is related to heterogeneity of the atmosphere in gravitation field of the Earth. It became possible to reveal the factor of gravity field due to the fact that in the equation of the state of atmosphere considered to be ideal gas, the entropy s is taken into consideration and is written down as ρ = (p, s) instead of generally accepted ρ = ρ(p) which is fair only for isentropic media and is not applicable to the Earth. Such approach enabled to determine that apart from adiabatic mechanism of generation of sound wave there exists isobaric one and exactly this mechanism leads to dependence of sound speed on altitude which is the same as dependence on density.
1. Introduction
Sound speed is a characteristic quantity of the medium included in the system of hydrodynamic (gas-dynamic) equations and plays a significant role in study of wave processes within it. Therefore, correct determination of its value is crucial in adequate description of generation and distribution of waves in media. According to the modern theory of sound wave density perturbation is considered as mass variation in constant volume without heat transfer i.e. adiabatically and therefore the speed of sound propagation is called adiabatic speed of sound. Pursuant to this representation speed of sound in atmosphere is calculated according to the formula 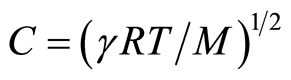 , i.e. depends only on temperature and does not depend on altitude. This result is dubious expressing that under the identical temperature conditions at the sea level and at an altitude of 100 km, where air density is 107 times less the speed of sound should have the same meaning. Figures 1 and 2 demonstrate graphs of dependence of atmosphere temperature of the Earth and sound speed at altitude in the range from of 0 to 85 km [1] which almost coincide. The same paper provides for the table demonstrating numerical meanings of sound speed at the altitudes of same interval and it is indicated that these meanings are calculated by means of the mentioned formula (Figure 13 shows the variation with altitude of the computed speed of sound). Internet provides for the same meaning of sound speed [2].
, i.e. depends only on temperature and does not depend on altitude. This result is dubious expressing that under the identical temperature conditions at the sea level and at an altitude of 100 km, where air density is 107 times less the speed of sound should have the same meaning. Figures 1 and 2 demonstrate graphs of dependence of atmosphere temperature of the Earth and sound speed at altitude in the range from of 0 to 85 km [1] which almost coincide. The same paper provides for the table demonstrating numerical meanings of sound speed at the altitudes of same interval and it is indicated that these meanings are calculated by means of the mentioned formula (Figure 13 shows the variation with altitude of the computed speed of sound). Internet provides for the same meaning of sound speed [2].
Such result is conditioned by incorrect definition of sound speed. As a matter of fact medium density may be

Figure 1. Molecular-scale temperature as a function of geopotencial altitude.
perturbed not only as a result of change mass in constant volume but by change of constant mass volume during temperature vibration under the conditions of constant pressure i.e. isobaricly. Therefore sound may have not only adiabatic but isobaric speed as well. Combination of these two speeds must result in dependence of sound speed on altitude which constitutes qualitatively new result.
Urgency of this consideration is proved by the fact of lack of information on experimental measurements of dependence of sound speed on altitude carried out with sufficient accuracy. The paper [3] provides for the results of measurement of sound speed at the see level for con-
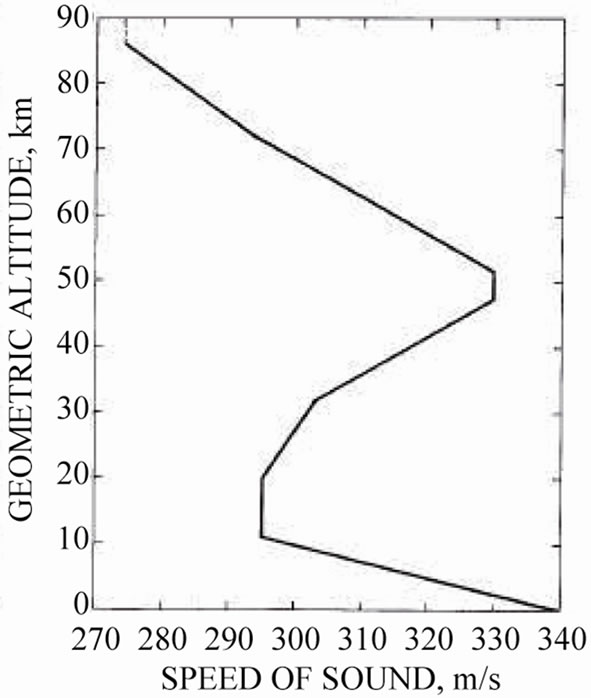
Figure 2. Speed of sound as function geometric altitude.
ditions t = 0˚C and p =1 atm and it is shown that it precisely coincides with theoretical results. In work [4] the method and results of measurement of speed of sound in atmosphere of the Earth by means of a probe are given. The schedule of dependence of sound speed on time of vertical movement of probe is demonstrated which does not enable us to precisely determine dependence of sound speed on altitude. Notwithstanding the aforesaid, approximate analysis shows that the numerical results of experiment are below the existing theoretical data which is beneficial for us but exceed the results calculated by means of our theory. Therefore, it is required to check our theory through precise experiment.
The first section of this article presents critical analysis of two typical works of famous authors. It is shown that their theory of sound waves is fair only for homogeneous medium and is not applicable to the Earth atmosphere. In the second section it is demonstrated that taking into consideration of nonisentropicity of ideal gas existing in external force field leads to the result that the ideal value of square of the sound speed is reduced from squares of adiabatic and isobaric speed sounds
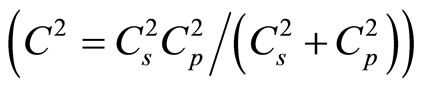 . The latter enables to provide correct definition of compressible and incompressible medium. In the third section it is shown that application of a new theory to the Earth atmosphere leads to dependence of sound speed in it on temperature as well as on altitude. A significant result is obtained evidencing that the upper bound of troposphere above which anomalous processes develop in atmosphere, coincides with the altitude where the values of adiabatic and isobaric speeds are equalized.
. The latter enables to provide correct definition of compressible and incompressible medium. In the third section it is shown that application of a new theory to the Earth atmosphere leads to dependence of sound speed in it on temperature as well as on altitude. A significant result is obtained evidencing that the upper bound of troposphere above which anomalous processes develop in atmosphere, coincides with the altitude where the values of adiabatic and isobaric speeds are equalized.
2. Modern Representations about Speed of a Sound in Atmosphere of the Earth and Inadequacy of Its Application
Motion of an ideal fluid (gas) in gravitational field of the Earth is described by the Euler's equation:
 (1.1)
(1.1)
In wave motions, speed v is considered for small value. Pressure p and density 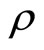 are represented in the form of the sum of their stationary
are represented in the form of the sum of their stationary 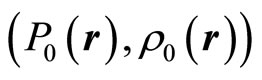 and perturbation values
and perturbation values , and therefore after lin-
, and therefore after lin-
earization of the Equation (1.1) we have:
 (1.2)
(1.2)
Let’s consider two examples of application of Equation (1.2) to sound waves which give clear representation of inadequacy of the current theory of sound waves in the Earth atmosphere.
In monographs [5,6] the Equation (1.2) is provided as follows:
 (1.3)
(1.3)
here it is implied that 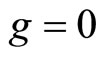 and
and 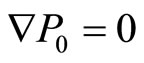 i.e. gravitational field does not affect the medium. This circumstance is highlighted in monograph [6], where it is indicated that under such approach the medium is isentropic, i.e. entropy
i.e. gravitational field does not affect the medium. This circumstance is highlighted in monograph [6], where it is indicated that under such approach the medium is isentropic, i.e. entropy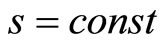 . The Equation (1.3) is solved together with the linearized equation of the continuity.
. The Equation (1.3) is solved together with the linearized equation of the continuity.
 (1.4)
(1.4)
When relation between perturbations of pressure and density are given by the formula
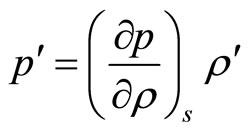 (1.5)
(1.5)
The index 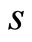 means, that the derivative undertakes at constant entropy. Whereupon the potential of speed is defined as
means, that the derivative undertakes at constant entropy. Whereupon the potential of speed is defined as 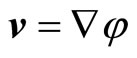 with the Equations (1.3)-(1.5) that leads to the wave equation:
with the Equations (1.3)-(1.5) that leads to the wave equation:
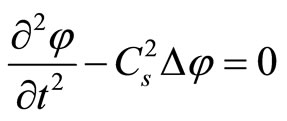 (1.6)
(1.6)
where quantity
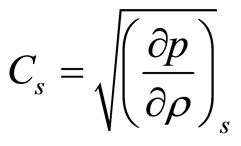 (1.7)
(1.7)
is defined as speed of adiabatic sound. Considering the air as ideal gas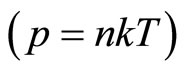 , and dependence between pressure and density in adiabatic process is defined by the following relation
, and dependence between pressure and density in adiabatic process is defined by the following relation
 (1.8)
(1.8)
where 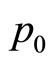 and
and  are initial values of pressure and density, and an adiabatic index
are initial values of pressure and density, and an adiabatic index 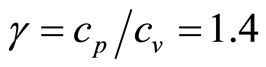 is ratio of thermal capacities (specific heath) for air in presence of constant pressure and volume respectively. From (1.7) for speed of sound following expression is derived:
is ratio of thermal capacities (specific heath) for air in presence of constant pressure and volume respectively. From (1.7) for speed of sound following expression is derived:
 (1.9)
(1.9)
Here R = 8.314 J/(mol·K) is a gas constant, m0 = 4.81·10–26 kg is mass of one air molecule and M = 29·10–3 kg/mol—mass of one mol air.
In monographies [7-9], the condition of static balance is applied to the Equation (1.2)
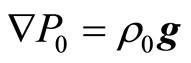 , (1.10)
, (1.10)
then it becomes:
 (1.11)
(1.11)
Then it is assumed, that gravitational acceleration 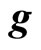 does not influence high-frequency sound fluctuations and the Equation (1.11) passes in the Equation (1.3). The authors supplement the Equations (1.3) and (1.4) with the equation of adiabatic process for ideal gas
does not influence high-frequency sound fluctuations and the Equation (1.11) passes in the Equation (1.3). The authors supplement the Equations (1.3) and (1.4) with the equation of adiabatic process for ideal gas
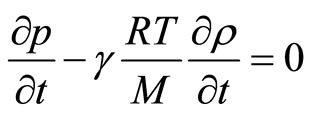 (1.12)
(1.12)
and representing all perturbed quantities in the form of a plane wave 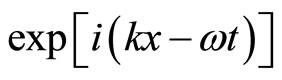 reduce these three equations to the wave equation relative to
reduce these three equations to the wave equation relative to 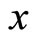 component of pretreated speed
component of pretreated speed
 (1.13)
(1.13)
from which, they obtain expression (1.9) for the speed of a sound, which presently is applied for both bottom (z ≤ 11 km) and top (11 km ≤ z ≤ 86 km) atmospheres.
Thus, in both cases authors try to define speed of a sound in atmosphere of the Earth from the wave equation for a plane wave with homogeneous phase speed, which depends only on temperature. It is well known, that to this equation satisfy intensity vectors of electric and magnetic fields of electromagnetic wave in vacuum. For which the vacuum is a homogeneous environment for its, consequently the velocity of light in it is homogeneous. Earth atmosphere is essentially heterogeneous medium for sound where all characteristic thermodynamic parameters depend on z coordinate. Since the sound of speed is also characteristic value of the medium, according to the fundamental principle of physics it must depend on z coordinate. Proceeding from the aforementioned, formulation and solution of the problem in the monographs [5,6] look correct, however they have no relation to a sound wave in atmosphere of the Earth. As for the resolution obtained in monographs [7-9], it can be easily shown that it is incorrect. Actually, in Euler’s linearized equation the authors apply condition of statistic balance (1.10) where
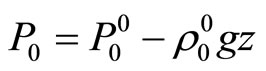 . (1.14)
. (1.14)
Here 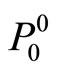 and
and 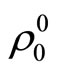 is values of pressure and density on a sea level. Expression (1.14) turns out from the general formula of distribution of pressure in atmosphere of the Earth
is values of pressure and density on a sea level. Expression (1.14) turns out from the general formula of distribution of pressure in atmosphere of the Earth
 , (1.15)
, (1.15)
where Laplace’s barometric formula for ideal gas is used
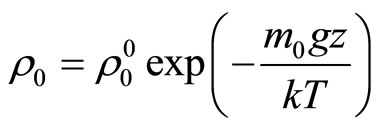 . (1.16)
. (1.16)
Assuming 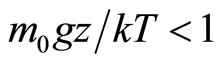 and representing (1.16) in series, we obtain (1.14) from (1.15) in linear approach. Thus, expression (1.14) is valid for the altitudes that fulfill inequality
and representing (1.16) in series, we obtain (1.14) from (1.15) in linear approach. Thus, expression (1.14) is valid for the altitudes that fulfill inequality
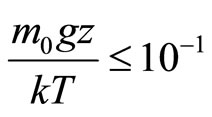 (1.17)
(1.17)
Assuming that T = 288.15 ˚K on a sea level, we find, that z ≤ 850 m. Thus, the Equation (1.14) is applicable in atmosphere only up to altitude of 850 m, or in water [9] where density practically does not depend on depth.
Besides, analysis of available literature obviously reveals one more significant contradiction related to determination of sound speed in the Earth’s atmosphere. In papers [10,11] the authors consider phenomena of sound dispersion and absorption. They deem that adiabatic speed of sound expressed by formula (1.9) makes no influence on the mentioned process and therefore, this speed of sound is called speed of sound of zero frequency. It is clear that this is a conventional name however it contradicts to the opinion of the authors of papers [6-9] stating that this speed complies with high frequency speed. The typical examples resulted above and ours comments show, that the existing theory of sound waves in atmosphere of the Earth demands revision.
3. The Reduced Speed of Sound
The sound wave transfers density perturbation at mechanical displacement of particles of medium. Pursuant to understanding established at present, atmosphere air represents ideal gas density of which depends only on pressure, i.e.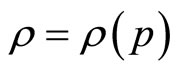 . In paper [6] it is noted that such approach is justified only for homogeneous medium in every point of which entropy has the same meaning (isentropic medium). It is apparent that the Earth’s atmosphere does not meet this condition and therefore
. In paper [6] it is noted that such approach is justified only for homogeneous medium in every point of which entropy has the same meaning (isentropic medium). It is apparent that the Earth’s atmosphere does not meet this condition and therefore . In terms of the aforementioned density perturbation should be put down as:
. In terms of the aforementioned density perturbation should be put down as:
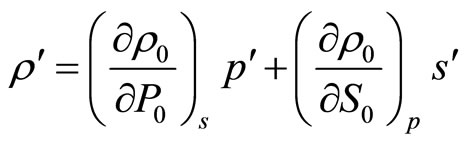 (2.1)
(2.1)
The first member in (2.1.) corresponds to density perturbation caused by mass alteration in fixed volume as a result of pressure perturbation in conditions of constant entropy, while the second member corresponds by volume alteration of fixed mass as a result of entropy perturbation in conditions of constant pressure. On the other hand, entropy perturbation is also callused by pressure perturbation, i.e.
 (2.2)
(2.2)
(2.1) and (2.2) give
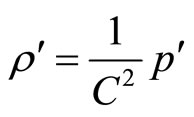 (2.3)
(2.3)
where
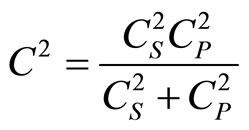 (2.4)
(2.4)
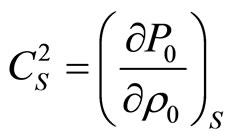 (2.5)
(2.5)
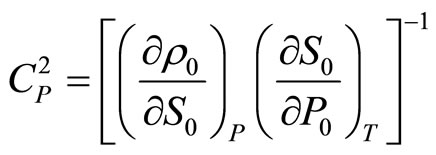 (2.6)
(2.6)
If expression (2.5) is called adiabatic speed of sound, it is logical to call expression (2.6) isobaric speed of sound since under thermodynamic relations
 and
and 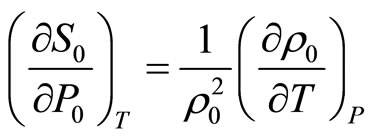
application for (2.6) results in
 (2.7)
(2.7)
(1.5) demonstrates that in homogeneous medium square of sound speed coincides with coefficient of connection of pressure and density perturbations. We assume that the same is fair for heterogeneous medium and therefore it should be defined by means of formula (2.4). We see that square of ideal value of sound speed equals to the reduced value of square of adiabatic and isobaric speeds. Such definition of sound speed—which is fair for any medium in the field of gravity, profoundly changes the existing notion on the sound itself and the medium. Pursuant to the latter, medium is considered incompressible if speed of sound in it is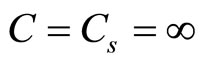 . At such definition of the incompressible medium, which model is often used in applied problems, equation of medium state (2.3) is fell out of the system of hydrodynamic (gas dynamic) equations and thus, it is not clear which medium is referred. Deriving from (2.4) medium is considered incompressible, if
. At such definition of the incompressible medium, which model is often used in applied problems, equation of medium state (2.3) is fell out of the system of hydrodynamic (gas dynamic) equations and thus, it is not clear which medium is referred. Deriving from (2.4) medium is considered incompressible, if  and then,
and then, 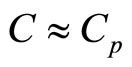 and for the compressed medium
and for the compressed medium 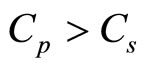 and
and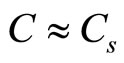 . Now, the concept of compressibility or incompressibility gets clear physical sense that has significant applied value.
. Now, the concept of compressibility or incompressibility gets clear physical sense that has significant applied value.
4. Speed of Sound in Atmosphere of the Earth
Atmosphere of the Earth represents multilayered structure and in each layer, dependences of physical parameters on geometrical altitude z are different. The chart provided for in Pic. 1, which can be found in internet [2] as well as in scientific literature [1;7] shows that in interval of altitudes from z = 0 to z = 11 km temperature changes under linear law  and in the interval from z = 51 km to z = 85 km approximately
and in the interval from z = 51 km to z = 85 km approximately  under the law. In intermediate interval (11 - 51 km) the temperature is either constant or increases, which makes us think that anomalous processes take place there. Besides, along with increase of altitude, deviation of experimental value to a greater index from the values calculated by means of formula (1.16) is also flaring. E.g. at the altitude z = 7.5 km where theoretical value of air density decreases e-times, relative error constitutes 23%, while when z = 11 km it constitutes 40%. At 35 km they equalize and thereafter theoretical value exceeds the experimental one and at the altitude of 85 km relative error constitutes 95%. In light of the aforementioned we assume that the model of ideal gas and consequently our theory can be applied up to 11 km altitude where temperature fall strictly obeys linear law. The aforesaid does not exclude possibility of its application in conditions of upper atmosphere.
under the law. In intermediate interval (11 - 51 km) the temperature is either constant or increases, which makes us think that anomalous processes take place there. Besides, along with increase of altitude, deviation of experimental value to a greater index from the values calculated by means of formula (1.16) is also flaring. E.g. at the altitude z = 7.5 km where theoretical value of air density decreases e-times, relative error constitutes 23%, while when z = 11 km it constitutes 40%. At 35 km they equalize and thereafter theoretical value exceeds the experimental one and at the altitude of 85 km relative error constitutes 95%. In light of the aforementioned we assume that the model of ideal gas and consequently our theory can be applied up to 11 km altitude where temperature fall strictly obeys linear law. The aforesaid does not exclude possibility of its application in conditions of upper atmosphere.
Let’s demonstrate that theoretical calculations shown above result in obvious dependence of sound speed on altitude in the Earth’s atmosphere. Indeed, for value Cs we have expression (1.9) while by application of (1.16) from (2.7) for Cp we get
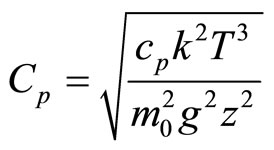 (3.1)
(3.1)
Substituting (1.9) and (3.1) in (2.4) expressions for speed of a sound in the specified layer (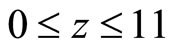 km) of the Earth atmosphere we receive
km) of the Earth atmosphere we receive
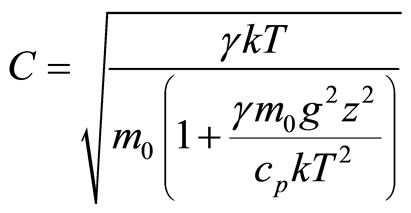 (3.2)
(3.2)
(3.2) shows that ideal value of sound speed in atmosphere obviously depends on altitude. Besides, we see that sound is adiabatic not only when g = 0 but when g ≠ 0 but z = 0. At removal from a sea level, dependence of speed of sound on altitude becomes evident which is caused by heterogeneity of the atmosphere. In Table 1, 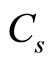 ,
, 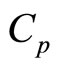 and
and 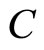 values are obtained by formulas (1.9), (3.1) and (3.2) in the range of altitudes from to
values are obtained by formulas (1.9), (3.1) and (3.2) in the range of altitudes from to  up to
up to 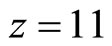 km, besides, corresponding values of speeds of sound
km, besides, corresponding values of speeds of sound 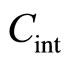 taken from the online calculator [2]. Values
taken from the online calculator [2]. Values 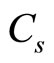 and
and 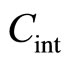 coincide, and relative errors between values
coincide, and relative errors between values 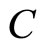 and
and  at altitudes of
at altitudes of 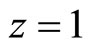 km and z = 11 km are equal to 0.3% and 33% respectively. It confirms our assumption that it is possible to consider sound to be adiabatic only up to altitude of
km and z = 11 km are equal to 0.3% and 33% respectively. It confirms our assumption that it is possible to consider sound to be adiabatic only up to altitude of 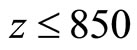 m. For visualization, dependences of
m. For visualization, dependences of  and
and 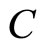 on
on 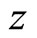 in intervals (0 - 1 km) and (1 - 11 km) are presented on the Figures 3 and 4 respectively. Let’s define the altitude on which
in intervals (0 - 1 km) and (1 - 11 km) are presented on the Figures 3 and 4 respectively. Let’s define the altitude on which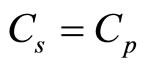 . From (3.2) it can be seen, that it is defined from a relation
. From (3.2) it can be seen, that it is defined from a relation
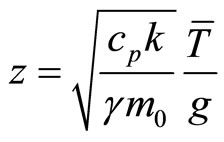 (3.3)
(3.3)
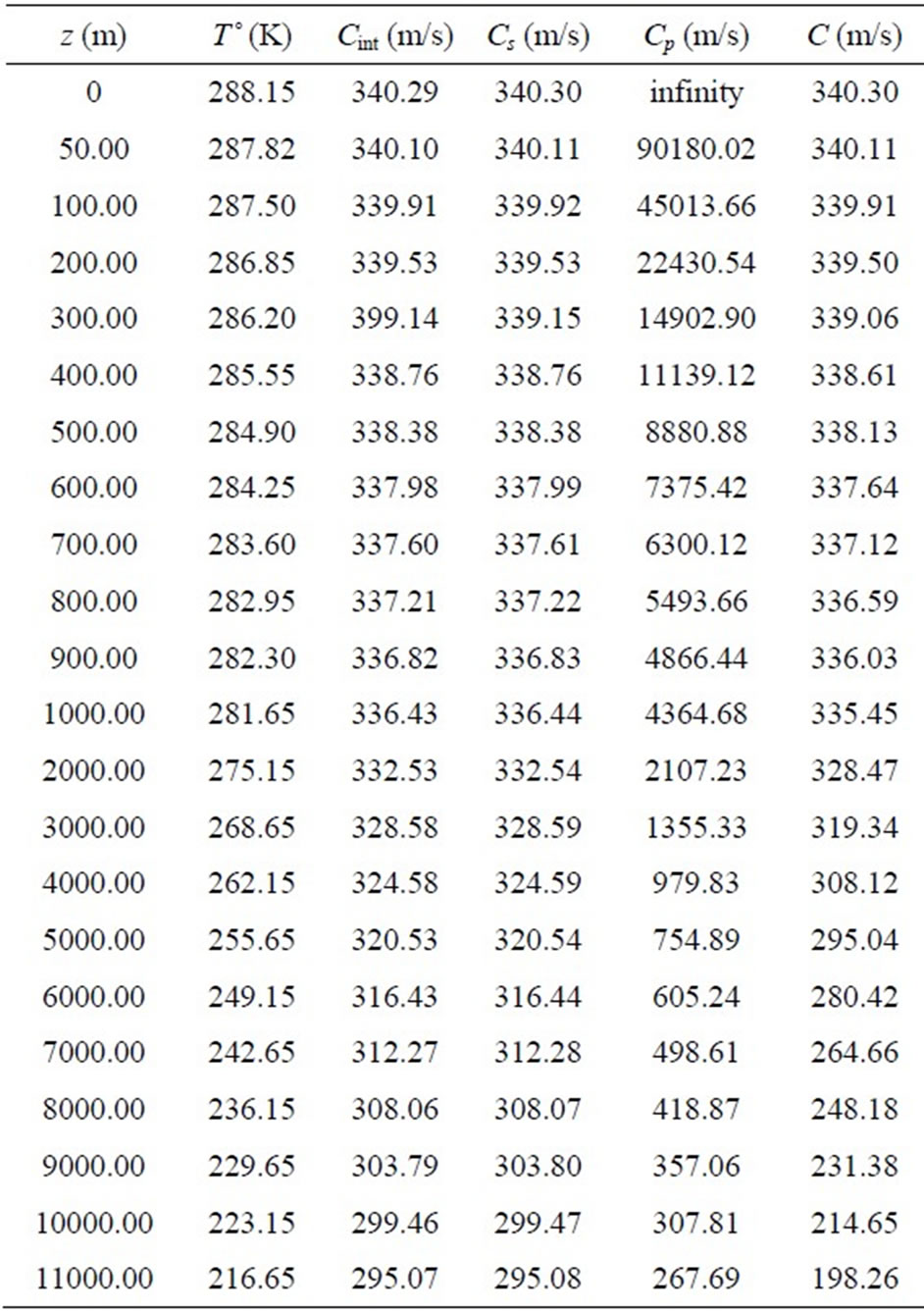
Table 1. Velocity values of Cs, Cp and C at altitudes from 0 toо 11,000 m; comparison with internet data (online calculator).

Figure 3. Dependence of Cs and C on altitude in the range z = 0 m to z = 1000 m.
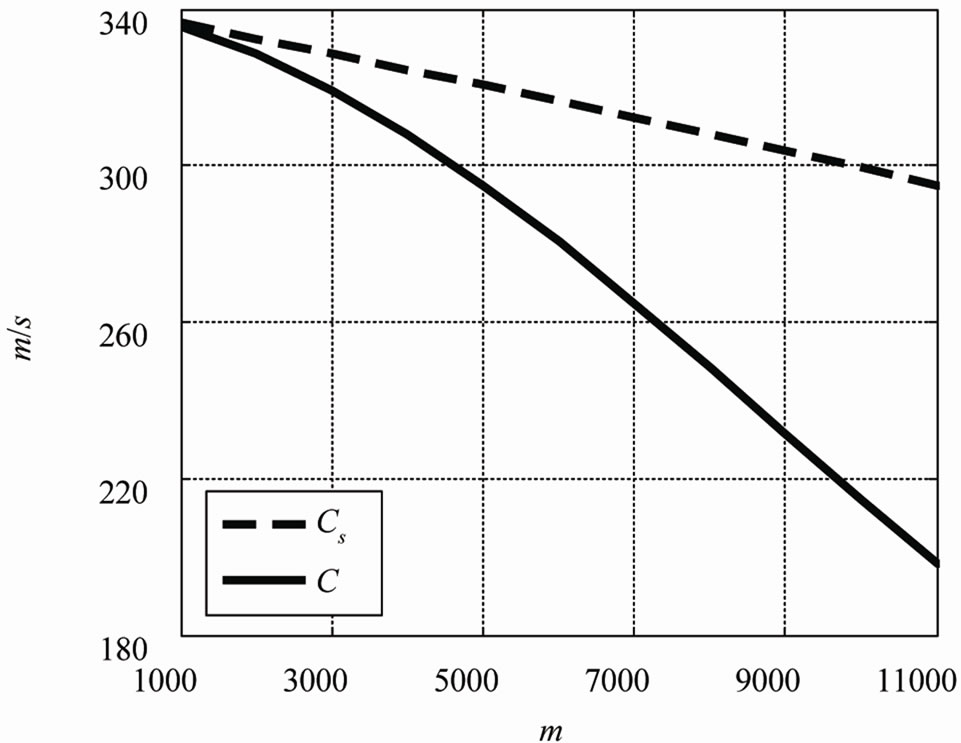
Figure 4. Dependence of Cs and C on altitude in the range z = 1000 m to z = 11,000 m.
Substituting values of constants (cp = 103 J/kgK) in (3.3) and assuming that average value of temperature in the mentioned interval is T = 252.4 ˚K, we receive z = 11.6 km. As we can see altitude on which adiabatic and isobaric speeds of sounds are equal, practically precisely coincides with altitude above which anomalistic processes occur in atmosphere. We think that it is not a casual coincidence and it has deep physical sense, definition of which is a subject of the further researches.
5. Conclusion
It is shown above that the existing theory on adiabatic sound in the Earth atmosphere is characterized by deficiencies related to incorrect definition of the sound speed which is understood as speed of distribution of adiabatic density perturbation of the medium. As a result, the sound speed in the Earth atmosphere depends only on temperature and does not depend on altitude while the density itself exponentially depends on it. As a matter of fact the density may be perturbed not only adiabaticaly, but isobaricaly as a result of entropy perturbation at perturbation of pressure leading to perturbation of temperature and consequently to isobaric alteration of the volume of the given air mass. All this finally results in dependence of sound speed on altitude pursuant to the formula (3.2). We assume that correction of the adiabatic wave theory suggested by us has an unconditional right to exist unless it is disproved by an experiment. However, if it is proved it will lay the foundation for qualitatively new research in gas and hydrodynamics.
REFERENCES
- U.S. Standard Atmosphere, National Aeronautics and Space Administration, 1976.
- http://www.digitaldutch.com/atmoscalc
- G. S. K. Wang, “Speed of Sound in Standard Air,” Journal of the Acoustical Society of America, Vol. 79, No. 5, 1986, pp. 1359-1366. doi:10.1121/1.393664
- G. Santostasi, et al., “A Student Designed Experiment Measuring the Speed of Sound as a Function of Altitude,” McNeese State University, Lake Charles, 2008.
- L. D. Landau and E. N. Lifshitz, “Nauka,” Theoretikal Physics, Hydrodynamics, Vol. 6, Moscow, 1988.
- A. D. Pirce, “Acoustics: An Introduction to Its Physical Principles and Applications,” Acoustical Society of America, New York, 1989.
- E. E. Gossard and W. H. Hooke, “Waves in the Atmosphere,” Elsevier, New York, 1975.
- L. M. B. C. Campos, “On Three-Dimensional Acoustic Gravity Waves in Model Non-Isothermal Atmospheres,” Wave Motion, Vol. 5, No. 1, 1983, pp. 1-14. doi:10.1016/0165-2125(83)90002-1
- M. J. Lighthill, “Waves in Fluids,” Cambridge University Press, Cambridge, 2002.

