World Journal of Engineering and Technology
Vol.03 No.04(2015), Article ID:60977,9 pages
10.4236/wjet.2015.34018
Performance Evaluation and Measurements of 3G Mobile Communication Networks: A Case Study
Kwame Agyeman-Prempeh Agyekum, Eric T. Tchao, Emmanuel Affum
Department of Electrical and Electronic Engineering, KNUST, Kumasi, Ghana

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 17 June 2015; accepted 7 November 2015; published 10 November 2015

ABSTRACT
Communication networks have undergone rapid developments in the past few decades in many Sub-Saharan African countries. The increasing number of subscribers and demand for greater variety of services in these countries make it difficult for network operators to provide the service varieties subscribers want while maintaining acceptable levels of quality of service. This paper analyzes the radio network of cellular networks in terms of traffic distribution over the existing number of communication channels using MATLAB/Simulink. A scale-free user network, which takes into account user behavior in a realistic physical network, has been used to model a more realistic cause for call blockings in a typical cellular network deployment under a Sub-Saharan environment. Peak recorded traffic distribution was observed to have overwhelmed the existing number of channels provided by the network operators for some cells eventually leading to increase in call drop rates. This high call blocking probability was attributed to poor network monitoring by the network operators to match the ever changing traffic intensities.
Keywords:
Traffic Analysis, Blocking Probability, Trunking Efficiency, Communication Channels, Scale-Free Networks

1. Introduction
The ever increasing demand for communication services has led to serious challenges to network operators to ensure acceptable Quality of Service (QOS) at minimum cost. In the Ghanaian communication industry and many emerging telecom markets in Sub-Saharan Africa, it is very necessary to take into consideration the competitive business environment that is arising as a result of the market liberalization and deregulation [1] . In order to effectively operate in these business environments, network operators must take into consideration the effective use of their available resources (channels) to deliver acceptable quality of service to subscribers at low tariffs. This will take effective network design and optimization models to achieve that.
Communication systems are capacity limited and as such, it can only support a limited amount of simultaneous traffic. In order to effectively plan networks with acceptable parameters such as blocking probability, handover blocking probability and utilization, traffic analysis that can reflect the true system behavior is indispensable [2] . In the past few decades, several traffic models for communication systems have been proposed. Models for traffic analysis based on traffic data fitting using appropriate algorithms under specified conditions in complex networks have been proposed in [3] and [4] . The set of conditions the authors in [4] specified however did not take into account the behavior of users in the modeled complex network. Hence the proposed model fails to establish a relationship with the actual physical processes that are responsible for user behaviors observed in the data.
Studies of small-world and scale-free properties of complex networks have been able to model the relationship between measured data and user behaviors and have been presented in [5] -[8] . Scale-free modeling of communication networks employs practical deployment scenarios based on certain specific network topologies that possess properties closely resembling those of realistic physical networks. Xia et al. in [9] observed that telephone traffic was affected by the network behavior on the user network. Results in [10] showed that the number of users and the number of calls made/received followed a power-law distribution which violated traditional traffic analysis. Authors in [11] showed that the process of radio network optimization could be significantly improved if the real user’s spatial distribution was known. This knowledge could allow an optimal assignment of radio resources to particular areas of the network.
In many cellular networks deployment in Sub-Saharan Africa, it will be difficult to determine the real subscriber’s spatial distribution because of the limited resources and the bad business model of the network operators as evident by the subscriber characteristics in [1] . Reliable and flexible performance evaluation techniques are therefore needed to efficiently allocate the resources in these networks. From the viewpoint of traditional traffic analysis, the users in a cellular network form a complex user network and the traffic performance of the system is strongly correlated with the behavior of its users [12] . The scale-free model has been identified as the appropriate model for these user networks which exhibits small-world and scale-free properties since the model establishes a clear connection between the user network behavior and the system traffic load.
This paper evaluates the performance of two communications networks in a typical Sub-Saharan African country in terms of offered traffic and the probability of call blocking over a scale-free user network. Together with measurements and analytical methods, the simulation-based evaluation of these networks will be increasingly important as the deployment of new mobile applications on these networks will impose new requirements both on the radio interface and the network infrastructure.
To model the relationship between user behaviors and field measured data without losing low-level details due to high-level abstraction, the scale free network model proposed in [13] will be used in analyzing field data in this study. In the next sections we will discuss the traffic model which has been chosen for the performance analysis of the mobile networks. The simulation parameters and the results of the study are subsequently presented.
2. Network Traffic Model
In a mobile cellular system, new calls are being initiated randomly according to a certain distribution. Each new call will involve a calling party and a receiving party. When the new call is established successfully, a pair of channels will be occupied and both the caller and the receiver will contribute the same amount of traffic to the system. The intensity of the offered traffic, denoted by A, can be calculated using E = 2λμ, where μ is the call departure rate and λ is the arrival rate of new calls [14] . In Figure 1, a detailed categorization of the offered traffic is shown. Among the offered traffic, part of it is carried by the network successfully. This portion of traffic is termed carried traffic. The rest belongs to lost traffic, which is caused by new call cancellations, new call blockings and handoff failures. The new call blockings can be further divided into those due to engaged receivers and those caused by limited channel capacity. In particular, the blockings caused by engaged receivers are closely related to the user network configuration. On the other hand, the handoff failures are dependent on the user mobility.
Figure 1. Network Traffic scenario; adapted from [13] .
Thus, both the user network model and the mobility model have an influence on the performance of the mobile cellular system. Suppose User i wants to initiate a new call. First, User i randomly chooses a user from his acquaintance list with equal probability. Assume that User j has been selected. If there is no channel available for either user, the call is blocked due to limited capacity. When channels are available for both users, the status of User j will be checked. If he is engaged, the call will be blocked due to an engaged receiver. Otherwise, the new call will be established successfully. When the call is in progress, the mobility of the users is under close monitoring. Whenever a user moves out of the original cell into a new cell, the availability of a free channel in the new cell will be checked. Suppose there is no free channel available, the ongoing call will be terminated due to a handoff failure. Otherwise, the user will release the channel of the serving cell and occupy a new channel of the new cell. The monitoring process will continue until the call is terminated either because the call is completed or a handoff has failed. In either case, the channels being occupied by users will be released. Conversation, the call initiation will not proceed. Such a call blocking is termed as new call cancellation.
3. Simulation Parameters
The variations in the number of user for the two networks within the survey areas are shown in Figure 2 and Figure 3. The number of request increases from April and reaches a threshold of 12,800,000 requests for communication resources in July whiles that for network B decrease gradually from 3,400,000 to 3,350,000 in April and decreases drastically from May to June. The request for Network B then increases again to it threshold from July to August. The reasons for this variation have been discussed thoroughly in [15] .
In order to effectively simulate the user behavior for the two networks, we considered a communication network of N users with these users located in C cells. The use of cells reflects the actual case in the two deployed communication networks. These N users will each have 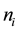 acquaintances. In modeling the scale-free user network, each user will have his own acquaintance list and a user can only call his acquaintances. The following two-step method is used to model the scale-free user network. First, the number of acquaintances
acquaintances. In modeling the scale-free user network, each user will have his own acquaintance list and a user can only call his acquaintances. The following two-step method is used to model the scale-free user network. First, the number of acquaintances 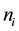 for user i is determined by a power-law distributed random number generator. Next, the acquaintance lists are filled by randomly selecting acquaintances. The relationship of acquaintance is bi-directed. If user i is selected as an acquaintance of user j, then user j is automatically added into user i’s acquaintance list. When a user is going to make a call, he randomly chooses a receiver from his acquaintance list. The probability that a user with more
for user i is determined by a power-law distributed random number generator. Next, the acquaintance lists are filled by randomly selecting acquaintances. The relationship of acquaintance is bi-directed. If user i is selected as an acquaintance of user j, then user j is automatically added into user i’s acquaintance list. When a user is going to make a call, he randomly chooses a receiver from his acquaintance list. The probability that a user with more
Figure 2. User request for Network A.
Figure 3. User request for Network B.
acquaintances makes/receives a call is higher and the mean value of this user’s inter-call time is smaller. We have also denoted the parameters of the communication system by following symbols:
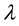 : referred as average arrival rate. The average calling rate measured in calls per hour.
: referred as average arrival rate. The average calling rate measured in calls per hour.
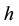 : The average holding time or service time h is the average duration of occupancy of a traffic path by a call. For voice traffic, it is the average holding time per call in hours or 100 seconds and for data traffic, average transmission per message in seconds.
: The average holding time or service time h is the average duration of occupancy of a traffic path by a call. For voice traffic, it is the average holding time per call in hours or 100 seconds and for data traffic, average transmission per message in seconds.
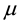 : service rate is the reciprocal of the average holding time in calls per hour
: service rate is the reciprocal of the average holding time in calls per hour
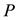 : constant of proportionality.
: constant of proportionality.
The simulation parameters based on the behaviors of users in the two networks have been summarized in Table 1.
The following assumptions were also made in the study:
• Call requests are memory less, implying that all users, including blocked users, may request a channel at any time.
• All free channels are fully available for servicing calls until all channels are occupied.
• The probability of a user occupying a channel (called the service time) is exponentially distributed. Longer calls are less likely to happen as described by an exponential distribution [16] .
• There are a finite number of channels available in the trunking pool. We denote the number of channels dedicated for voice calls within the cell and handover calls by x and the number of channels dedicated for han-
Table 1. Simulation parameters.
dover calls only by s.
• Traffic requests are described by a Poisson distribution which implies exponentially distributed call inter- arrival times.
We also consider k possible state, where k is a discrete random process representing the number of occupied or busy channels at discrete time. The probability of observing the system in state (k) is denoted by:
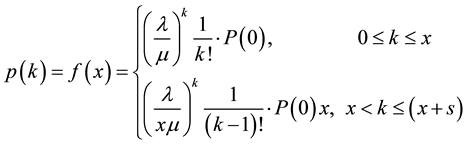 (1)
(1)
The state probability equation in (1) can be normalized as:
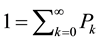 (2)
(2)
The probability that all the channels are busy is represented by a fraction of block calls. This is evaluated as:
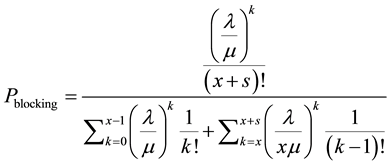
4. Results and Analysis
Data was obtained from two areas, Location 1 and Location 2, in the urban center of Accra-Ghana for a period of 30 days. From the field measurements and the simulation parameters, the stochastic variations associated with number of calls and service times were analyzed with MATLAB/Simulink. In order to obtain numerically significant data to reduce errors in probability estimation from relative frequencies, a number of sectors in the networks within the measurement areas have been considered. The sectors considered in this study were chosen based on the number of served subscribers in the area, traffic load and the way users move in and out of these sectors.
From the blocking probability and trunking efficiency simulation results, call blockings are controlled by two factors, user engagement and limited number of channels. The effects of these two factors are clearly shown in Figures 4-8. From the results obtained for networks A and B, as the number of channels increases, some of the arrived calls will be successfully set up, hence, the call blocking probability for the scale-free user network declines more rapidly. The blocking probabilities measured in the sectors for the two networks at Location 1 and Location 2 for a period of 30 days are summarized in Figure 9, Figure 10, Table 2 and Table 3. When the number of trunks is limited, almost all call requests are blocked as validated by measurements of Network A: Cell AD0181E and Network A: Cell AD0181D which is far above the threshold specified by the National
Figure 4. Probability of blocking for Network A sites at Location 1.
Figure 5. Trunking efficiencies for Network A sites at Location 1.
Figure 6. Probability of blocking for Network B sites at Location 1.
Communications Authority (NCA). Hence the greater the number of channels; the lower the blocking probability of the user network. The results also show that the traffic for a scale-free user network differs significantly
Figure 7. Trunking efficiencies for Network B sites at Location 1.
Figure 8. Trunking efficiencies for Network A sites at Location 2.
Figure 9. Probability of blocking measurements at Location 1.
from that for the fully-connected user network, analyzed by authors in [17] , which is usually assumed in classical traffic analysis. Because of the scale-free nature of human networks, analysis based on a scale-free user network reflects a more realistic traffic scenario. From the trunking efficiency simulation results for the two net
Figure 10. Probability of blocking measurements at Location 2.
Table 2. Summary of network performance at Location 1.
Table 3. Summary of network performance at Location 2.
works, it can be seen that before the capacity reaches the threshold, the trunking efficiency decreases as network capacity increases which is due to high network request rate. When the channel capacity reaches the threshold, the trunking efficiency is almost fixed.
Generally it can be seen that, higher blocking probability for a scale-free user network is caused by call concentration by a number of users who have a relatively large number of acquaintances. The results show that, in addition to inadequate channel capacity, the user behavior has a profound influence on call blockings. For example, the high call drop rates experienced in Network A could be as a cause of the operator’s inability to match the increasing demand of communication resources made by subscribers to the available channels. Increasing the capacity of Network A which generally exhibited poor network performance may not necessarily solve the problem if the user behavior is not considered in the optimization process.
5. Conclusions
Traffic analysis of two communication networks based on a scale-free network model under a typical deployment scenario has been studied in this work. The blocking probabilities of the networks were simulated and compared with field measured results. The results in this study validate the assertion that the behavior of users and the channel capacity produce a significant impact on the performance of communication networks.
The peak recorded traffic distributions were observed to have overwhelmed the existing number of channels provided by the Network operator whose users had a large number of acquaintances eventually leading to increase in call drop rates. This high call blocking probability was attributed to poor network monitoring by the network operators to match the ever changing traffic intensities especially. Based on the findings, efficient channel allocation schemes have been implemented on the networks to manage a balance relationship between cost incurred by operators and services offered to the subscribers. The effects of these strategies will be analyzed and presented when enough data are available.
Cite this paper
Kwame Agyeman-PrempehAgyekum,Eric T.Tchao,EmmanuelAffum, (2015) Performance Evaluation and Measurements of 3G Mobile Communication Networks: A Case Study. World Journal of Engineering and Technology,03,176-184. doi: 10.4236/wjet.2015.34018
References
- 1. Agyekum, K., Tchao, E.T. and Affum, E. (2013) Evaluation of Mobile Number Portability Implementation in Ghana. International Journal of Computer Science and Telecommunications, 4, 30-33.
- 2. Anurag, K., Manjunath, D. and Kuri, J. (2004) Communication Networking: An Analytical Approach. Elsevier/Morgan Kaufmann, Amsterdam.
- 3. Aiello, W., Chung, F. and Lu, L. (2000) A Random Graph Model for Massive Graphs. Proceedings of 32nd Annual ACM Symposium on Theory of Computing, New York, April 2000, 171-180.
http://dx.doi.org/10.1145/335305.335326 - 4. D’Agostino, R.B. and Stephens, M.A., Eds. (1986) Goodness-of-Fit Techniques. Marcel Dekker, New York, 63-93, 97-145.
- 5. Veitch, D. and Arby, P. (2001) A Statistical Test for the Time Constancy of Scaling Exponents. IEEE Transactions on Signal Processing, 49, 2325-2334.
http://dx.doi.org/10.1109/78.950788 - 6. Newman, M.E.J. (2003) The Structure and Function of Complex Networks. SIAM Review, 45, 167-256.
http://dx.doi.org/10.1137/S003614450342480 - 7. Moltchanov, D. (2009) Performance Evaluation and Traffic Modeling. Traffic and QoS Management in Wireless Multimedia Networks, 31, 89-150.
http://dx.doi.org/10.1007/978-0-387-85573-8_3 - 8. Albert, R. and Barabási, A.L. (2002) Statistical Mechanics of Complex Networks. Reviews of Modern Physics, 74, 47-97.
http://dx.doi.org/10.1103/RevModPhys.74.47 - 9. Xia, Y.X., Tse, C.K., Tam, W.M., Lau, F.C.M. and Small, M. (2005) Scale-Free User Network Approach to Telephone Network Traffic Analysis. Physical Review E, 72, 1-6.
http://dx.doi.org/10.1103/PhysRevE.72.026116 - 10. Pavlidou, F.-N. (1994) Two-Dimensional Traffic Models for Cellular Mobile Systems. IEEE Transactions on Communications, 42, 1505-1511.
http://dx.doi.org/10.1109/tcomm.1994.582831 - 11. Georgeta, B., Cornel, B., Adrian, B. and Eugen, M. (2009) Traffic Models and Associated Parameters in GSM/(E)GPRS Networks. Wseas Transaction on Communications, 8, 833-841.
- 12. Cornel, B., Georgeta, B. and Adrian, B. (2010) Mixed Traffic Models for Dimensioning Radio Resources in GSM/ GPRS Networks. Wseas Transaction on Communications, 9, 233-242.
- 13. Tam, W.M., Lau, F.C.M., Tse, C.K., Xia, Y.X. and Small, M. (2005) Traffic Analysis of a Mobile Communication System Based on a Scale-Free User Network. 2005 International Symposium on Nonlinear Theory and Its Applications (NOLTA2005), Bruges, 18-21 October 2005, 130-133.
- 14. Thompson, R.A. (2000) Telephone Switching Systems. Artech House, Boston.
- 15. Agyekum, K., Tchao, E.T. and Affum, E. (2013) Customer Experience with Mobile Number Portability Implementation in Ghana. International Journal of Emerging Technology and Advanced Engineering, 3, 663-667.
- 16. Bellamy, J.C. (2000) Digital Telephony. Wiley, New York.
- 17. Sharp, D.S., Cackov, N., Laskovic, N., Shao, Q. and Trajkovic, L. (2004) Analysis of Public Safety Traffic on Trunked Land Mobile Radio Systems. IEEE Journal on selected Areas in Communications, 22, 1197-1205.
http://dx.doi.org/10.1109/JSAC.2004.829339












