World Journal of Engineering and Technology
Vol.03 No.03(2015), Article ID:57920,5 pages
10.4236/wjet.2015.33011
Trajectory Planning and Optimal Lateral Stability Control under Multiple Barriers for Intelligent Vehicle
Zhonghua Zhang, Xuecai Yu*, Zhijie Jin, Yejun Ying, Rongwei Hua, Xuwei Lin
School of Engineering, Zhejiang Normal University, Jinhua, China
Email: *yuxczjnu@126.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 May 2015; accepted 10 July 2015; published 14 July 2015
ABSTRACT
Based on analysis and evaluation on the circular, cosine type, constant-speed offset type and lad- der type lane change trajectory, this paper proposes an intelligent vehicle lane change trajectory model under multiple barriers, proposes its dynamic constraints in the light of the cellular automata theory, obtains the desired lane change trajectory using this method, and finally changes into a simple coefficient selection problem. Secondly, based on the quadratic optimal control theory, this paper proposes a state space analysis method of intelligent vehicle lateral control, and designs an optimal controller for lateral stability of H2 vehicles. The computer simulation results show that compared with other vehicle trajectory methods, the method in this paper is able to simply and rapidly describe the trajectory, and can describe the intelligent vehicle lane change trajectory under a variety of situations, wherein the controller is reliable and capable of fast con- vergence.
Keywords:
Intelligent Vehicle, Motion Planning, Optimal Control, Cellular Automata, Computer Simulation

1. Introduction
China is one of the developing countries with sustained economic growth in the world, and has remained more than 7% economic growth rate since 1991 [1] . With the rapid economic growth and the improvement of the people’s living standards, the vehicle parc in China has continued rapid growth, where the growth of private car ownership is significant. By June this year, the car ownership in the whole China reaches 53.56 million, including 32.39 million private cars. According to the statistical data of the Ministry of Construction, the private car ownership of China is growing at an annual average rate of about 20% [2] - [4] . How to solve the security problems in the process of the car running is extremely urgent. According to related statistics, the traffic accidents caused by vehicle lane change account for about 4% to 10% of all traffic accidents, resulting in unnegligible traffic delay and economic losses. At present, the proportion of the traffic accidents caused by vehicle lane change in all traffic accidents is increasing year by year. Especially, the number of traffic accidents caused by traffic lane change on express highway rapidly grows, so it is necessary to research the safe trajectory of the intelligent vehicle lane change [5] .
At present, the research on intelligent vehicle lane change for overtaking mainly includes macroscopic and microscopic traffic flow simulation, lane change early warning, simplifying automatic control of the vehicle lane change, and so on [6] . The research is increasingly mature, but because of the complexity of the vehicle lane change, no method is available to simply and accurately reflect the process and trajectory of the vehicle lane change as yet. On the basis of preliminary researches, this paper tries to study the vehicle lane change trajectory by simplifying the barriers and expressing the lane change trajectory with the principle of cellular automata, which considers not only the horizontal and longitudinal control in the planned path, but also the dynamic constraints, so that the description of the intelligent vehicle lane change trajectory for overtaking is converted into the problems of how to simplify barriers and select polynomial coefficients [7] .
1.1. Research Status & Strength and Weakness of the Existing Methods
At present, the research on intelligent vehicle lane change for overtaking mainly includes macroscopic and microscopic traffic flow simulation, lane change early warning, simplifying automatic control of the vehicle lane change, and so on. Early lane change model only considers whether the front and back gap on the target lane meets the safe running requirements, and implements lane change if so [8] . That is to say, the front and back gap is fixed as a parameter of the simulation system without considering the horizontal and longitudinal control problems and other dynamic constraints in the process of the vehicle lane change. As early as in 1986, Gripps published a paper, which proposes a lane change model on urban roads from the perspective of the driving purpose and safety to introduce the concept of the vehicle lane change trajectory. Later, Wonshik Chee, Caywood, et al. respectively investigated the concept and analysis model of the lane change, put forward the lateral acceleration and acceleration gradient of circular and cosine trajectory etc., and took the vehicle speed as one of the system design parameters. The weakness of the existing methods is listed as follows:
(1) Circular trajectory is one of the simplest trajectories with the strength of short trajectory planning time and weakness of poor smoothness;
(2) Cosine trajectory assumes that the curve consists of two cosine type trajectories, is characterized by good smoothness, but suffers from large accumulated error;
(3) Constant-speed offset planning trajectory is characterized by simple planning method, is easy to get the optimal solution of parameters, but is difficult to be put into engineering practice under real road conditions;
(4) Trapezoidal acceleration lane change trajectory can better satisfy the continuous curvature change and the change rate restrictions during moving from the angle of lateral acceleration of the vehicle with lane change, but is not flexible. For example, it is difficult to regulate the lane change process.
1.2. Intelligent Vehicle Lane Change Trajectory with Multiple Barriers
In case of autonomous driving of an intelligent vehicle, multiple obstacles, if any, may be split into several independent individual barriers using the idea of breaking up the whole into parts, and then processed using the above-mentioned algorithm of a single barrier, so that the number of suitable lane change trajectory is reduced accordingly, because under this situation it is necessary to consider not only the constraints of a single barrier, but also the impact of lane change on the next barrier [9] .
Problem Description. In general, the vehicle lane change involves a controlled vehicle (vehicle “c”), a vehicle on the current lane (vehicle “o1”) and two vehicles on the target lane (vehicles “o2” and “o3”), as shown in Figure 1. Under the circumstances, two schemes are available for the controlled vehicle to complete the lane change, and the specific choice depends on the speed of the vehicles on the target lane and the distance between them and the controlled vehicle.
Dynamic Constraints. As can be seen from the above discussion, as long as the barriers are identified in the
Figure 1. Problem description of intelligent vehicle lane change trajectory for overtaking with multiple barriers.
parameter space, it is very easy to choose a suitable trajectory. This section will discuss the dynamic constraints brought about by dynamic changes of the vehicles [10] .
In fact, the highest horizontal acceleration and longitudinal acceleration interact and influence one another. Here, a more conservative approach is adopted under the assumption that a vehicle can reach the maximum critical acceleration as follows:
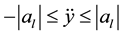 (1)
(1)
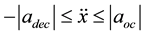 (2)
(2)
where  is the maximum critical acceleration in the direction y. So,
is the maximum critical acceleration in the direction y. So,  and
and 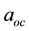 is the maximum critical acceleration in the direction X.
is the maximum critical acceleration in the direction X.
In order to associate the maximum acceleration with the polynomial selection, the following steps are adopted: the above-mentioned polynomial coefficient only depends on the boundary conditions and should not be changed, so the lateral acceleration arising from the boundary conditions follows the above standard. The Equation (1) is first subject to quadratic differential. If at least one of its maximum values and minimum values is beyond the above scope, then it is necessary to change the boundary conditions (i.e. the final situation). In practical operation, it may be available by checking the table of correspondence between the time of completing lane change and the final horizontal position.
If the designed lateral acceleration is guaranteed to be feasible, then it is necessary to select appropriate polynomial parameter values for calculation of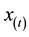 , and get the following longitudinal acceleration after differential:
, and get the following longitudinal acceleration after differential:
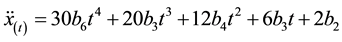 (3)
(3)
Then it is possible to get:
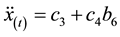 (4)
(4)
where, c3 and c4 are respectively a function of time and boundary conditions, namely a new function of b6, so the corresponding dynamic constraints shall satisfy the following formula:
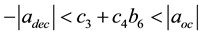 (5)
(5)
So the root of Equation (5) is drawn, and then a polynomial parameter within permissible range is selected to ensure that it is within the above constraints, which will be proved by examples as follows.
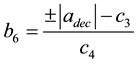 (6)
(6)
The above situation is still taken as an example: the initial and terminal vehicle states are available from Equations (7). For simplification, the vehicles on the target lane are neglected, the order of the polynomial  is increased, and the limit of acceleration available for the vehicle is as follows:
is increased, and the limit of acceleration available for the vehicle is as follows:
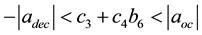 (7)
(7)
In this case, the dynamic states are also identified on the figure as barriers, so they can be regarded as practical barriers. Obviously, it becomes very easy to choose a feasible trajectory at this time. Control strategy of intelligent vehicle lane change trajectory for overtaking under multiple barriers was shown as Figure 2. Faster and slower strategy was included in this research.
Principle of Cellular Automata. Cellular Automata (CA for short) is essentially a dynamical system that is defined in a cellular space composed of discrete cells in a finite state, and is evolved in discrete time dimension according to certain local rules. The cellular automata is not determined by strictly defined physical equations or functions, but composed of a series of model construction rules. Any model following these rules can be counted as a cellular automata model.
From the Figure 3, the principle and evolution results of cellular automata were shown. It is the basic for the optimizing for control parameters.
The position curve is shown in Figure 4 and Figure 5. The result shows that in the whole process of motion:
(1) The position shows smooth transition without sharp points and crude points in the trajectory;
(2) Both horizontal position and longitudinal position reach the target position within expected time.
2. Controller Design
Robust stability of the yaw velocity helps to ensure the lateral stability of the vehicle itself, and then lay the foundation for steering control of the whole vehicle system according to the navigation information. This paper establishes a mathematical model for vehicle steering control in the light of the kinematic model of two degrees of freedom, kinematic model of preview, and dynamic property function of steering of vehicles, and designs the optimal steering controller of H2 based on the linear quadratic optimal control theory.
Selection of the optimal control rate mainly refers to determination of the performance index function, and is
Figure 2. Control strategy of intelligent vehicle lane change trajectory for overtaking under multiple barriers.
Figure 3. Principle and evolution results of cellular automata.
essentially the optimal control under certain performance indexes. For an actual control system, shift from an initial state to a goal set can be realized by a variety of different control functions, and it is first necessary to determine a performance index for evaluation on the control effect to find an optimal control law from feasible control functions. The computer simulation results in Figure 6 show that the navigation deviation (direction deviation and lateral deviation) and other state variables all shows fast convergence, and the controller plays a significant role in correction. Because of the path tracking was shocked, the positive and minus error were both appeared in simulation.
3. Conclusion
In this text, we proposed an intelligent vehicle lane change trajectory model under multiple barriers, proposes its dynamic constraints in the light of the cellular automata theory, obtains the desired lane change trajectory using this method, and finally changes into a simple coefficient selection problem.
The cellular automata and the optimal control theory were used in controller design. By the simulation result,
Figure 4. Position in x-direction.
Figure 5. Position in y-direction.
Figure 6. Computer simulation results of the optimal controller.
it shows that the controller is reliable and capable of fast convergence.
Acknowledgements
The project was supported by the Zhejiang Provincial Natural Science Foundation of China (Granted No. LY13E080010), and by the Jinhua civic Bureau of Science and Technology under Grant No.
Cite this paper
ZhonghuaZhang,XuecaiYu,ZhijieJin,YejunYing,RongweiHua,XuweiLin, (2015) Trajectory Planning and Optimal Lateral Stability Control under Multiple Barriers for Intelligent Vehicle. World Journal of Engineering and Technology,03,100-105. doi: 10.4236/wjet.2015.33011
References
- 1. Garnell, P. (1980) Guided Weapon Gontrol Systems. Pergamon Press, Oxford.
- 2. Jiang, Z.P. (1997) Tracking Control of Mobile Robots: A Case Study in Backstepping. Automation, 33, 1393-1399.
http://dx.doi.org/10.1016/S0005-1098(97)00055-1 - 3. Frerro, R. (1995) Control of a Nonholorxrmic Mobile Robot: Backstepping Kinematics into Dynamics. IEEE Proceedings of 34th Conference on Decision and Control, 3805-3810.
- 4. Takemura, N., Nakamura, Y. and Ishiguro, H. (2011) A Path Planning Method for Human Tracking Agents Using Variable-Term Prediction Based on Dynamic K-Nearest Neighbor Algorithm. 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), San Francisco, 25-30 September 2011, 2867-2872.
- 5. Tomar, R.S., Verma, S., Kushwah, R.S. and Tomar, G.S. (2013) Collision Avoidance Warning for Safe Lane Change. 2013 International Conference on Communication Systems and Network Technologies (CSNT), 385-389.
- 6. Vale, A., Fonte, D., Valente, F. and Ribeiro, I. (2014) Trajectory Optimization for Autonomous Mobile Robots in ITER. Robotics and Autonomous Systems, 62, 871-888.
http://dx.doi.org/10.1016/j.robot.2014.01.007 - 7. You, F., Wang, R. and Zhang, R. (2013) Study of System Identification and Control Algorithm for Intelligent Vehicle. China Journal of Highway and Transport, 21, 111-116.
- 8. Zhang, R.H., Ge, P.S., Zhou, X., et al. (2013) An Method for Vehicle-Flow Detection and Tracking in Real-Time Based on Gaussian Mixture Distribution. Advances in Mechanical Engineering, 2013, Article ID: 861321.
- 9. You, F., Zhang, R.H., Wang, H.W., et al. (2014) Dynamic Model and Tracking Control of Tractor Semi-Trailer Vehicle with Underactuated System. Journal of Jilin University (Engineering and Technology Edition), 44, 1296-1302.
- 10. Kim, S., Oh, H., Suk, J. and Tsourdos, A. (2014) Coordinated Trajectory Planning for Efficient Communication Relay Using Multiple UAVs. Control Engineering Practice, 29, 42-49.
http://dx.doi.org/10.1016/j.conengprac.2014.04.003
NOTES
*Corresponding author.








