Journal of Electronics Cooling and Thermal Control
Vol. 3 No. 2 (2013) , Article ID: 33067 , 16 pages DOI:10.4236/jectc.2013.32008
An Unsteady Mixed Convection in a Driven Cavity Filled with Nanofluids Using an Externally Oscillating Lid
Mechanical Engineering Department, University College of Engineering, University of Tehran, Tehran, Iran
Email: *rahimyan@ut.ac.ir
Copyright © 2013 Arian Jafari et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 24, 2013; revised May 25, 2013; accepted June 2, 2013
Keywords: Mixed Convection; Unsteady; Cavity; Grashof Number; Reynolds Number; Lid Frequency; Solid Volume Fraction
ABSTRACT
A numerical investigation of an unsteady, periodic, laminar mixed-convection in a cavity utilized with copper-water nanofluid is presented. In this study both top and bottom walls are assumed to be isolated, meanwhile sidewalls are considered under constant temperature condition. We consider a time-dependent oscillating wall on top to fulfill a periodic mixed-convection inside the cavity. In this type of problems both Grashof and Reynolds numbers play a great role in flow pattern and heat transfer characteristics, so we focus our study on four major parameters that can be crucial such as Grashof 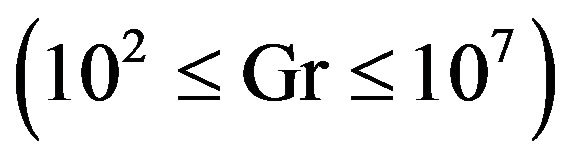 and Reynolds
and Reynolds 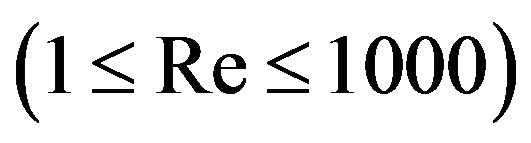 numbers, solid volume fraction
numbers, solid volume fraction 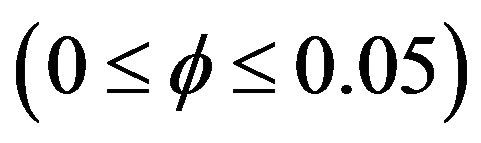 and the non-dimensional lid frequency
and the non-dimensional lid frequency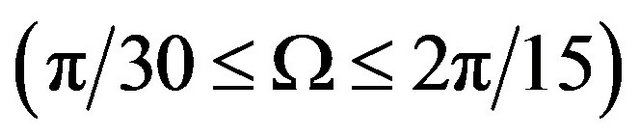 . The obtained results show that the augmentation of Reynolds number and Grashof number would enhance the average Nusselt number. It is also found that unlike steady state condition, at high Reynolds numbers, as lid is moving in the negative direction the average Nusselt number on the hot wall becomes higher in respect to the case that lid is moving in the positive direction due to thermal boundary layer disturbance. Lid frequency does not have a significant effect on thermal characteristics at low Reynolds numbers, meanwhile at higher Reynolds numbers, increment of lid frequency results in heat transfer reduction. Moreover, solid volume fraction is found to have better efficiency at higher Grashof numbers.
. The obtained results show that the augmentation of Reynolds number and Grashof number would enhance the average Nusselt number. It is also found that unlike steady state condition, at high Reynolds numbers, as lid is moving in the negative direction the average Nusselt number on the hot wall becomes higher in respect to the case that lid is moving in the positive direction due to thermal boundary layer disturbance. Lid frequency does not have a significant effect on thermal characteristics at low Reynolds numbers, meanwhile at higher Reynolds numbers, increment of lid frequency results in heat transfer reduction. Moreover, solid volume fraction is found to have better efficiency at higher Grashof numbers.
1. Introduction
Over the past several years, natural and mixed convection in a cavity filled with fluid has received a remarkable attention because of its wide and practical applications in real world engineering concerns [1-10]. These concerns can be observed in various fields such as cooling of electronic packages, solar energy collectors, ventilation and heating of living space and cooling of nuclear reactors (as an internal heat generator example) [11,12]. The first investigation about natural convection was probably conducted by G. De Vahl Davis et al. [13]. They studied flow and heat transfer in a cavity by considering different aspect ratios. Fusegi et al. [14] presented a numerical solution by solving natural convection governing equations at different Prandtl numbers to investigate heat transfer characteristics under various aspect ratios of a rectangular enclosure. Although many studies focus on rectangular or square enclosures, many numerical works have been done on wavy enclosures in order to investigate the effects of wavy walls on heat transfer capacity. Oztop et al. [15] numerically studied the effects of volumetric heat sources on natural convection heat transfer and flow structures in a wavy-walled enclosure. They showed that by augmenting the wave amplitude of the wavy wall, the rate of heat transfer would be higher. In mixed convection problems, the parameters that effect heat transfer are Gr, Re, and Pr (Rayleigh and Pr in natural convection). Gr and Re are usually simplified as a single parameter named Ri. It is obvious that variation in Ri number will be obtained by changing Gr and Re number either together or separately. It has been reported that the Nusselt number in a lid-driven cavity increases with augmentation of Pr while other effective parameters such as Re and Gr are kept constant [16]. For a fixed Pr, the Nusselt number increases with heightening Gr or Re while Re or Gr is kept constant respectively [17,18]. Sharifi [17] numerically studied laminar mixed heat convection in two-dimensional shallow rectangular driven cavities of aspect ratio 10. He showed that a primary vortex is observed at the right-hand side where the shear driven flow by the top moving lid is impacted on the right-hand sidewall and is forced to move downward along the sidewall. Some minor vortices are also formed in the cavity for Ri < 1. The local Nusselt number at the heated moving lid starts with a high value and decreases rapidly and monotonically to a small one towards the right side. Many cavity problems studied in literature have constant wall temperature accompanied by insulated walls (vertical or horizontal walls) [19,20]; these conditions can only be obtained if evaporation or condensation takes place on the wall’s surfaces (on constant temperature walls), but in real problem reaching these aims is a bit far from reality; in order to have a good control on the heat flux, we can consider a time-dependent driven-lid or mixed convection as a useful tool in our design’s effectual parameters. However, many recent studies of the lid-driven cavity flows are focused mainly on the problems with a constant velocity lid. Only a few works were involved with a vibrating lid. Nishimura and Kunitsugu [21] performed numerical investigation of the fluid mixing and mass transfer in two-dimensional rectangular cavities affected by the time-periodic lid velocity. Soh and Goodrich [22] outlined the basic transient flow features relevant to this problem using a time accurate finite-difference scheme. Moreover, Iwatsu et al. [23] performed a numerical investigation on the effect of external excitation on the flow structure in a square cavity. The results of their research have shown similar flow structure to steady driven-cavity flows when exerting small frequency values. A subsequent work by Iwatsu et al. [24] investigates a numerical study of the viscous flow in a heated driven-cavity under thermal stratification, where the oscillating lid was maintained at a higher temperature than the lower wall. The results of their work revealed substantial enhancement in the heat transfer rate at particular lid frequency values. Khanafer et al. [25] studied an unsteady laminar mixed convection heat transfer in a lid driven cavity. They found that the Reynolds number and Grashof number either increase or impede the energy transport process, and relatively small lid oscillation values were found to have more penetration force inside the cavity. Another concern about cavity problems relies on low thermal conductivity of fluid used in enclosures. Thus, the heat transfer capacity through such systems is relatively limited, and it is of importance to improve it from the industrial and energy concern point of view. To overcome this problem using nanosized particles able to dissolve in base flow has attracted tremendous attentions recently [26-28]. The way these particles enhance heat transfer capacity is that metallic nano-sized particles have high thermal conductivity comparing to base flow, so the mixture of nano-sized particles and base flow has high convective and conductive capacity. Therefore it is enriched with both solid and fluid properties. According to what stated about nanofluid advantages, many studies and investigations both numerically and experimentally have been done in recent years considering nanofluids. The first study concerning natural convection of a nanofluid confined in a differentially heated enclosure seems to be done by Khanafer et al. [29]. A comparative study of different models based on the thermophysical properties of copper-water nanofluid was developed and investigated. Results obtained from their numerical investigation indicate that the suspended nanoparticles significantly augment the heat transfer rate at any given Grashof number. A heat transfer correlation of the average Nusselt number for various Grashof numbers and volume fractions was proposed by the authors. Mahmoudi et al. [30] applied a model to simulate the natural convection utilized by two separate heat sources in an open cavity subjected to the copperwater nanofluid. They use a model developed by Brinkman [31] to determine mixture viscosity. They showed that the Nusselt number increases due to augmentation in Rayleigh number, the distance between two heat sources, and spacing from the wall. They also showed that the average Nusselt number increases linearly with the solid volume fraction increment of nanoparticles.
The main objective of the present paper is to investigate flow and heat transfer characteristics of an unsteady laminar mixed convection heat transfer in a cavity filled with nanofluid that is insulated from below and top walls and heated and cooled by exerting hot and cold constant temperature on vertical walls. The paper is organized as follows. In the next sections, the mathematical formulation of the problem is presented. Numerical solution and algorithm validation are then proposed. The effects of varying the Reynolds number, Grashof number, the lid frequency, and solid volume fraction on streamlines, isotherms, and temporal average Nusselt number will be illustrated and discussed. The last section contains some concluding remarks.
2. Mathematical Formulation
An unsteady, periodic, laminar, incompressible mixed convection in a two-dimensional square cavity filled with Newtonian nanofluids is considered for the present study. Physical dimensions are given in Figure 1. Both top and bottom walls are assumed to be adiabatic meanwhile other two vertical sidewalls are kept at constant temperature (hot temperature at the left wall and cold temperature at the right one). The top wall of the cavity is allowed to oscillate with a velocity u = u0 sinωt in its own place longitudinally, where u0 is the maximum
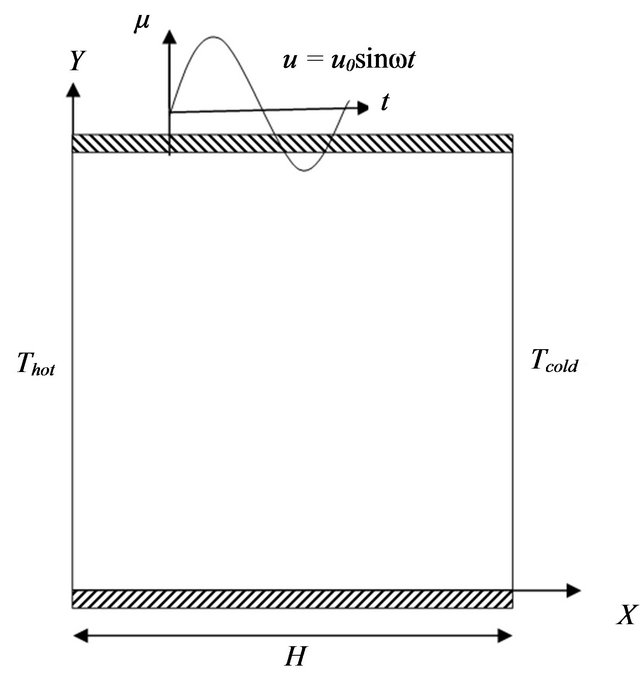
Figure 1. A schematic diagram of the physical model.
oscillating speed of the lid and ω is the oscillating frequency.
The thermo-physical properties of the nanofluids, considered in this study, given in Table 1, are assumed constant except for the density in the buoyancy force which varies linearly with temperature as
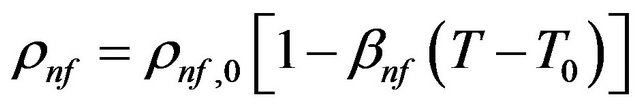
according to Boussinesq approximation, where 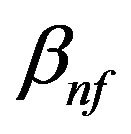 is the thermal expansion coefficient of nanofluid and subscript 0 denotes the reference state. It is also assumed that both the base flow and nanoparticles are in thermal equilibrium and no slip occurs between them. The shape and size of solid particles are assumed to be uniform and the diameter of them to be equal to 100 nm. The no-slip condition is imposed at the solid walls. It is further assumed that viscous dissipation is neglected in this study. Based on the abovementioned considerations, the unsteady governing equations for conservations of mass, momentum and energy are expressed in the following format:
is the thermal expansion coefficient of nanofluid and subscript 0 denotes the reference state. It is also assumed that both the base flow and nanoparticles are in thermal equilibrium and no slip occurs between them. The shape and size of solid particles are assumed to be uniform and the diameter of them to be equal to 100 nm. The no-slip condition is imposed at the solid walls. It is further assumed that viscous dissipation is neglected in this study. Based on the abovementioned considerations, the unsteady governing equations for conservations of mass, momentum and energy are expressed in the following format:
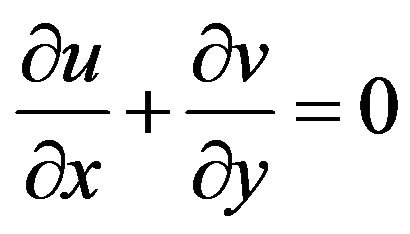 (1)
(1)
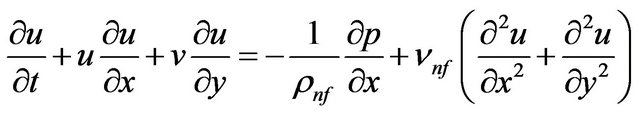 (2)
(2)
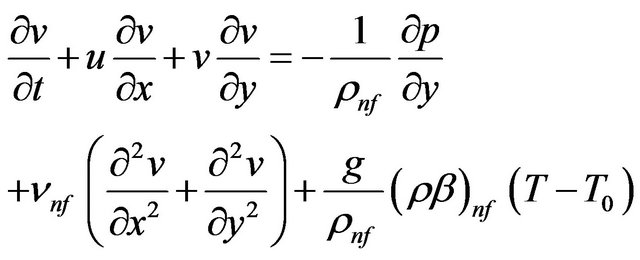 (3)
(3)
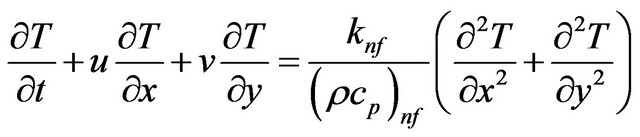 (4)
(4)

Table 1. Thermophysical properties of water and copper nanoparticles.
The effective density of nanofluid can be determined as:
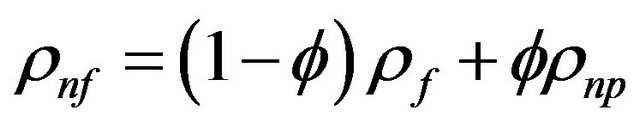 (5)
(5)
where 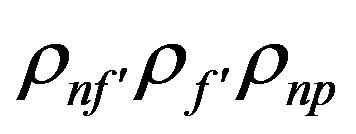 and
and 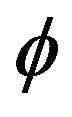 are nanofluid density, density of base fluid, density of nanoparticles, and solid volume fraction of the nanoparticles, respectively.
are nanofluid density, density of base fluid, density of nanoparticles, and solid volume fraction of the nanoparticles, respectively.
The thermal diffusivity of the nanofluid is:
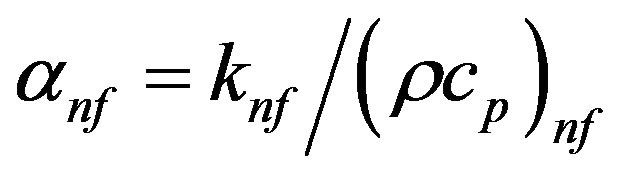 (6)
(6)
where the heat capacitance of the nanofluid can be given as:
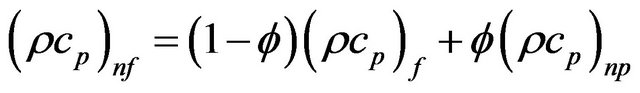 (7)
(7)
nanofluid thermal expansion coefficient can be determined by:
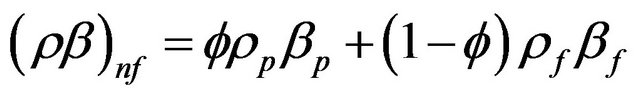 (8)
(8)
The effective thermal conductivity of nanofluid was suggested by Patel et al. [32] as follows:
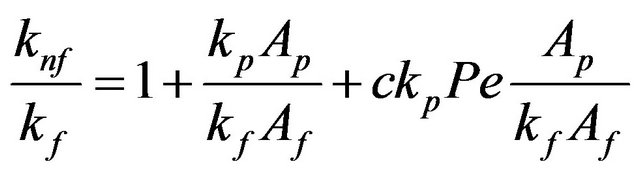 (9)
(9)
where c is constant and must be determined experimentally, according to Hemanth [33] 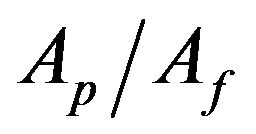 and Pe are defined as:
and Pe are defined as:
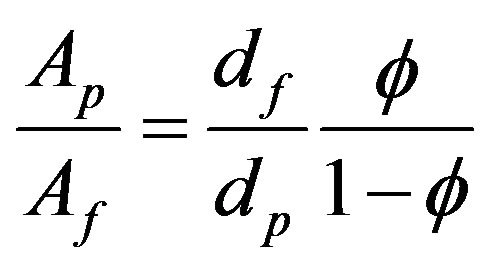 (10)
(10)
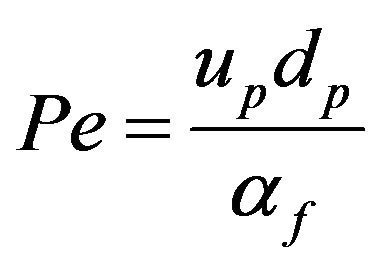 (11)
(11)
where dp is the diameter of nano-particles (in this study 100 nm) and df is the molecular size of base fluid (2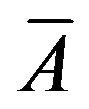 for water). up is the Brownian motion of particles given by [34]:
for water). up is the Brownian motion of particles given by [34]:
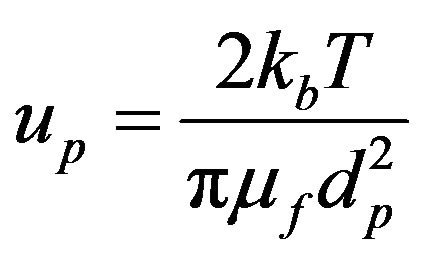 (12)
(12)
where kb is the Boltzmann constant.
The effective dynamic viscosity of the nanofluid was introduced by Brinkman as follows:
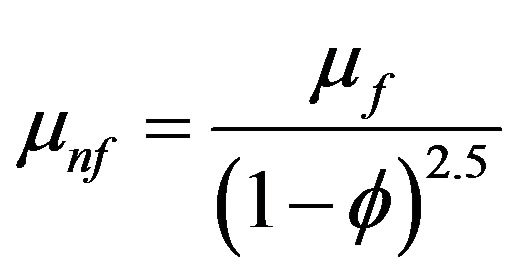 (13)
(13)
We can rewrite governing equations as non-dimensional form as below:
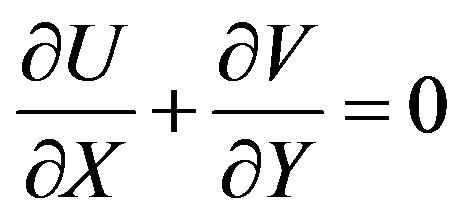 (14)
(14)
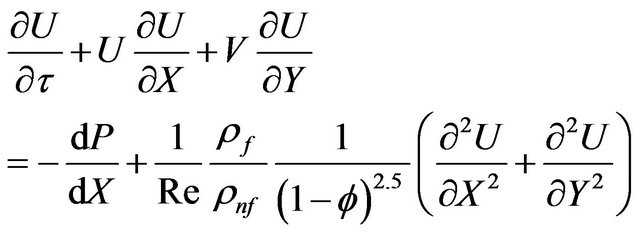 (15)
(15)
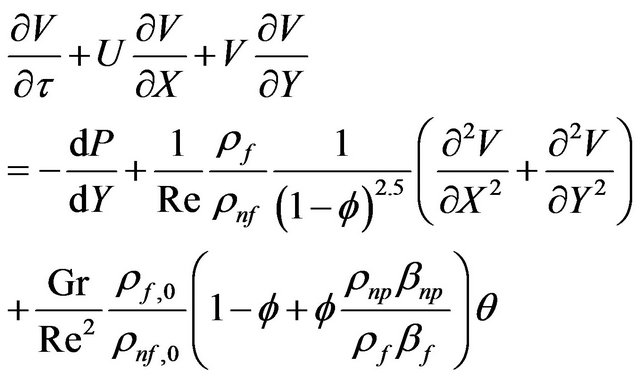 (16)
(16)
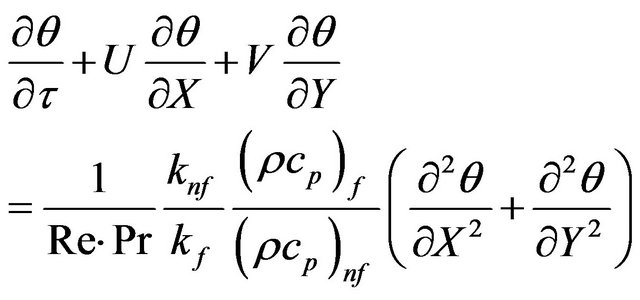 (17)
(17)
Here, the non-dimensional variables are: U the Xcomponent velocity, V the Y-component velocity, θ the temperature, and τ the time. Gr is the Grashof number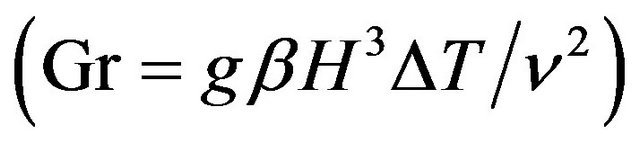 , Re is the Reynolds number
, Re is the Reynolds number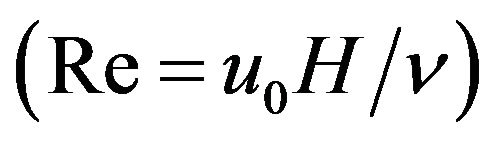 , and Pr is the Prandtl number
, and Pr is the Prandtl number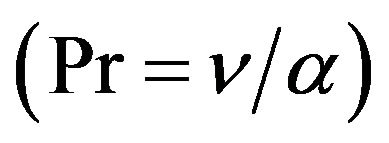 . The dimensionless variables in the above equations are defined as:
. The dimensionless variables in the above equations are defined as:
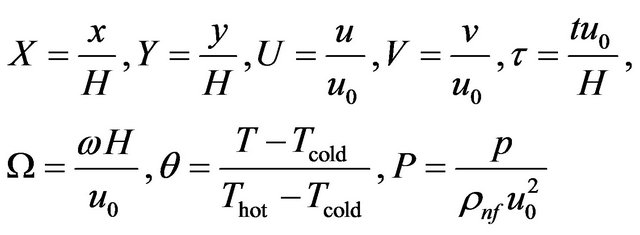 (18)
(18)
For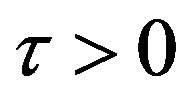 , the stagnation state
, the stagnation state 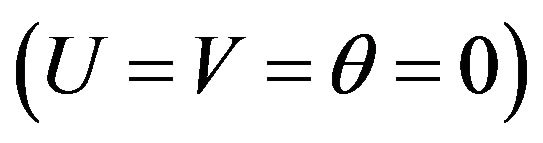 for temperature and flow fields is used as an initial condition for the sinusoidal-oscillating lid in this investigation. Meanwhile, the used dimensionless boundary conditions are summarized as follows:
for temperature and flow fields is used as an initial condition for the sinusoidal-oscillating lid in this investigation. Meanwhile, the used dimensionless boundary conditions are summarized as follows:
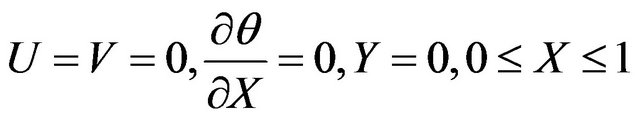 (19)
(19)
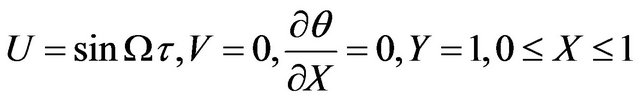 (20)
(20)
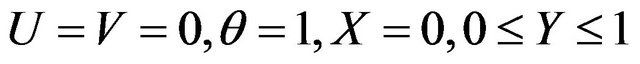 (21)
(21)
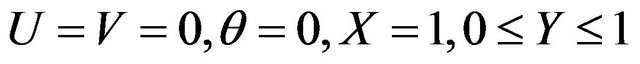 (22)
(22)
The time history of the dimensionless heat flux is computed through calculating the average Nusselt number along both the hot and cold sidewalls using:
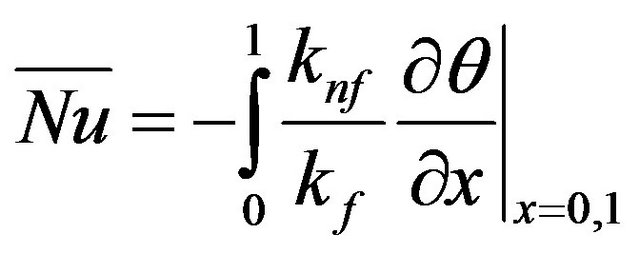 (23)
(23)
3. Numerical Solution
The solution of the governing equations along with the initial and boundary conditions is obtained using a control volume approach and SIMPLE algorithm with a staggered grid. The hybrid scheme is used to evaluate the flow, heat and mass fluxes across each of the control volume boundaries. In this study a non-uniform grid mesh which is finer near the boundaries is used, in order to have better accuracy in final results. An implicit scheme is employed to deal with the time differential terms. A line-by-line SOR method with relaxation is used in conjunction with iterations to solve the nonlinear discretized equations. The convergence of solutions is assumed when the relative error for each variable between consecutive iterations is recorded below the convergence criterion ε such that:
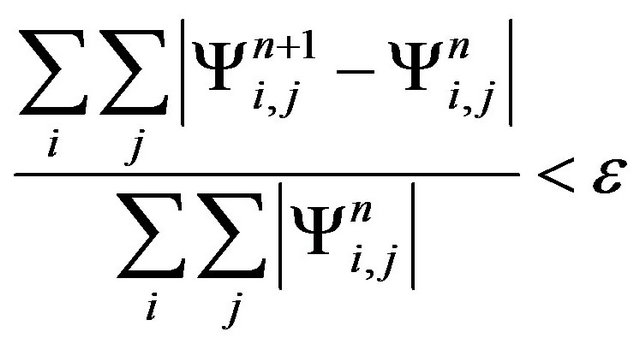 (34)
(34)
where n is the number of iteration index and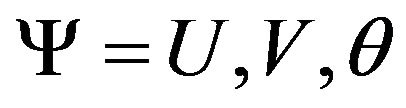 . The convergence criterion was set to 10–5.
. The convergence criterion was set to 10–5.
4. Algorithm Validation
A non-uniform mesh size system of 52 × 52 is put into practice in the present study with finer mesh near the cavity walls in order to capture accurate results. Table 2 shows the number of grid points and their influence on the maximum temporal average Nusselt number while lid moves at its maximum speed. First, the present numerical solution is verified against two well-known numerical studies. Namely, the numerical solutions of natural convection in a cavity reported by De Vahl Davis [13] and N. Massarotti et al. [35]. The findings of the comparisons are written down in Table 3 for the bounds on the magnitude of the average Nusselt number predictions. Both comparisons illustrate close proximity in the predictions made between the various solutions. Another fold for validation of our code is comparison between the predicted stream function contours under steady state pure fluid mixed convection of the present work to that of F. Talebi et al. [36]. As displayed in Figure 2, the comparison strikes a superb concurrence between both studies.
5. Results and Discussion
As stated earlier, the overall objective of the current study is to survey a time dependent two-dimensional

Table 2. Influence of number of grid for a test case at Re = 100, Gr = 106, f = 0.0, Ω = π/30.

Table 3. Comparison of the average Nusselt number at the hot wall between the present solution and other solutions.
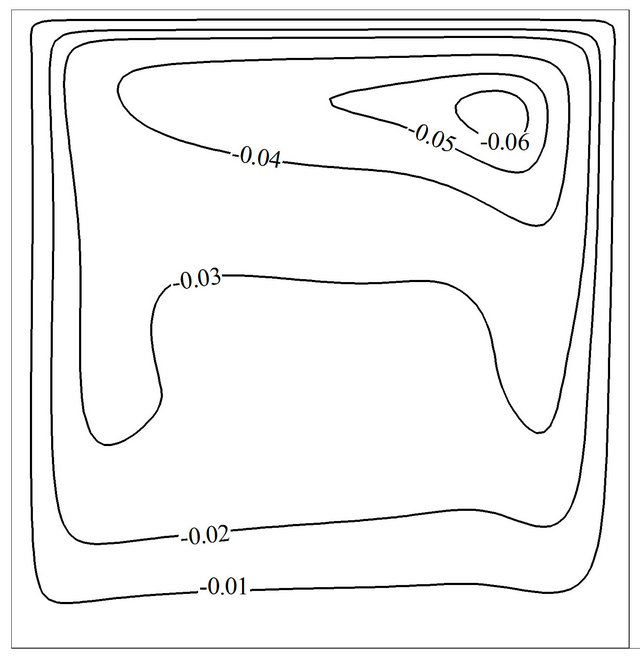 (a)
(a)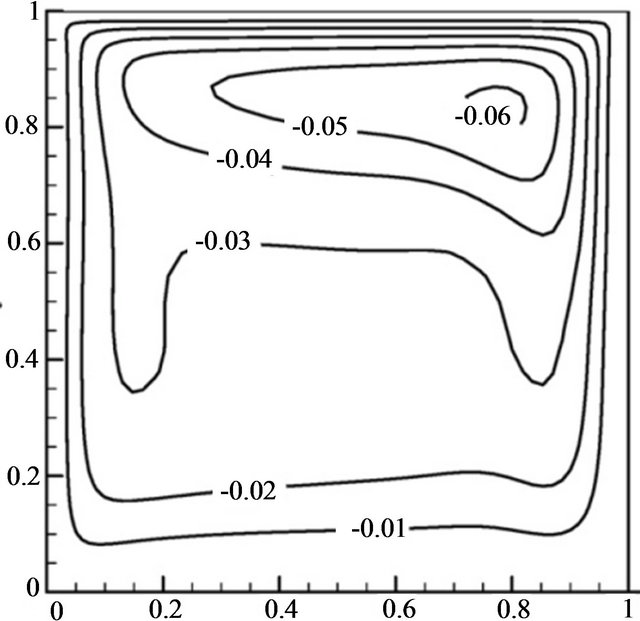 (b)
(b)
Figure 2. Comparison of the steady state mixed convection stream function between the present work (a) and Talebi [36] (b) for Re = 100, Gr = 2.1 × 105.
mixed convection in a lid-driven cavity utilized with nano-particles according to various Reynolds number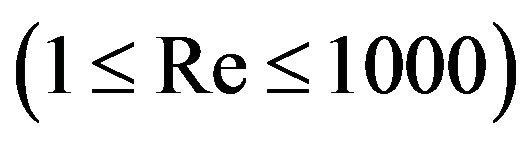 , Grashof number
, Grashof number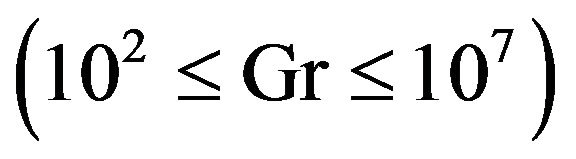 , lid oscillation frequency
, lid oscillation frequency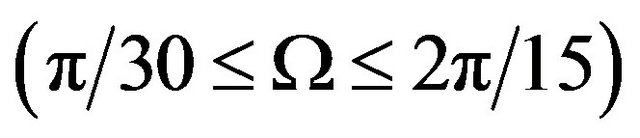 , and solid volume fraction
, and solid volume fraction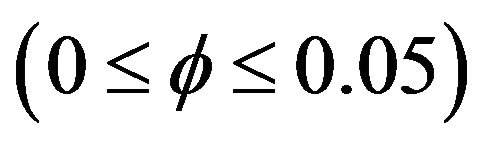 . In this part, all discussion is based on focusing on the hot wall due to the same periodic trend on the cold wall. In order to have a better comprehension of the average Nusselt number variation, average Nusselt number at the steady state mixed convection inside the cavity is written in Table 4 for both cases of u = 1, u = –1, and numerous Reynolds and Grashof numbers. According to Table 4, by increasing Grashof number, average Nusselt number tends to be equal in both cases.
. In this part, all discussion is based on focusing on the hot wall due to the same periodic trend on the cold wall. In order to have a better comprehension of the average Nusselt number variation, average Nusselt number at the steady state mixed convection inside the cavity is written in Table 4 for both cases of u = 1, u = –1, and numerous Reynolds and Grashof numbers. According to Table 4, by increasing Grashof number, average Nusselt number tends to be equal in both cases.
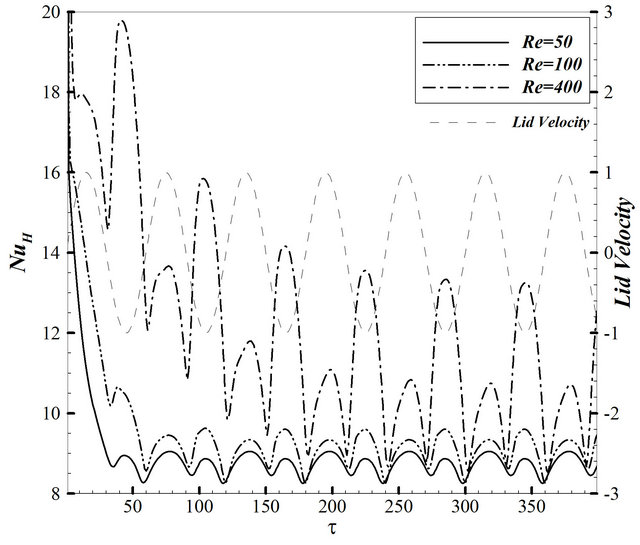
Figure 3 shows the impact of variations of Reynolds number on the temporal average Nusselt number along the hot wall while Grashof number and non-dimensional lid frequency are fixed at 105(a), 106(b) and π/30 respectively.
As illustrated In Figure 3(a), at relatively high Reynolds numbers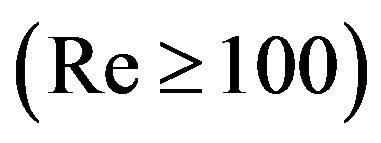 , the average Nusselt number has two maximums and two minimums in each time period. The greater maximum occurs whilst lid is at its highest negative speed value, because at this moment thermal boundary layer produced by buoyancy force will be disturbed by the flow motivated by lid about upper
, the average Nusselt number has two maximums and two minimums in each time period. The greater maximum occurs whilst lid is at its highest negative speed value, because at this moment thermal boundary layer produced by buoyancy force will be disturbed by the flow motivated by lid about upper
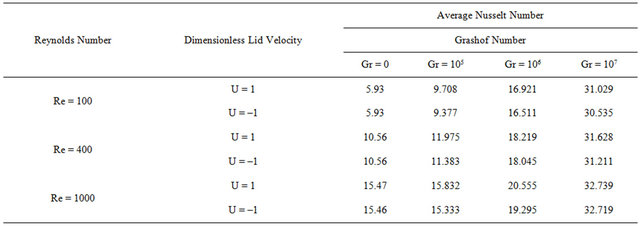
Table 4. Steady state average Nusselt number according to Reynolds and Grashof number variation for both case of lid velocity (u = ±1).
 (a)
(a) (b)
(b)
Figure 3. Variation of the average Nusselt number at different Grashof and Reynolds numbers: (a) Gr = 105, Ω = π/30, f = 0%; (b) Gr = 106, Ω = π/30, f = 0%.
half part of the hot wall. The inferior maximum takes place at maximum positive speed value of lid due to forced and free convection operation in the same direction. Although in this case these two forces operate in the same direction and enhance heat transfer on the hot wall, the effect of boundary layer disturbance caused by negative speed is more effectual that results in higher maximum Nusselt number. When lid stops in order to switch its velocity from positive to negative value and vice versa, two minimums come into sight due to lack of forced convection. As it is evident in Figure 3(a), by increasing Reynolds number, the temporal average Nusselt number will follow the same periodic behavior, but the difference between two maximums becomes more remarkable. It can be deduced that in high Reynolds numbers, thermal boundary layer disturbance turn in to be more outstanding. Figure 4 shows streamlines and isotherms for various velocities equal to 1, 0+, –1, and 0– at Re = 100 and fixed value of Gr = 105, and Ω = π/30. As it can be seen in Figure 4(a), natural convection and forced convection effects are accumulated and a big vortex is created inside the domain. This vortex makes up a narrow thermal boundary layer near upper part of the cold wall. On the contrary, thermal boundary layer stretches near upper part of the hot wall and causes a reduction of the local Nusselt number over there, but an increase in the average Nusselt number yields on the hot wall (inferior maximum) due to overall reduction of thermal boundary layer thickness along the hot wall. When the lid gradually decelerates to become stagnant, it can be observed in Figure 4(b) that natural convection is dominant inside the cavity due to lack of adequate forced convection. In
 (a)
(a)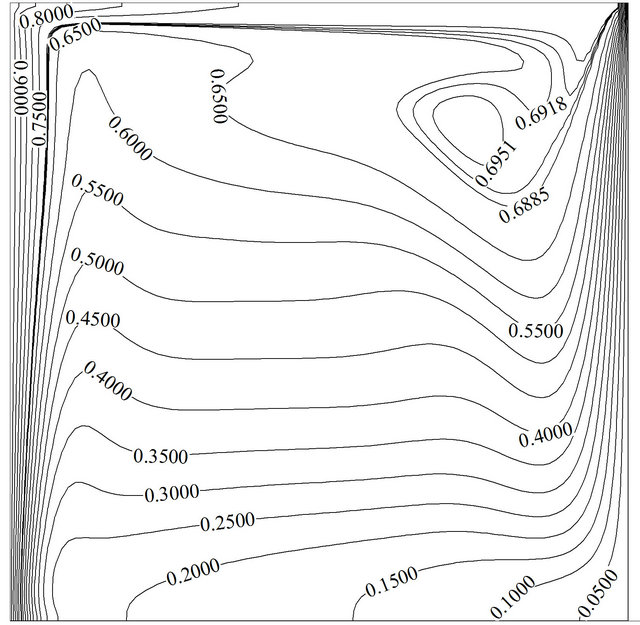 (b)
(b)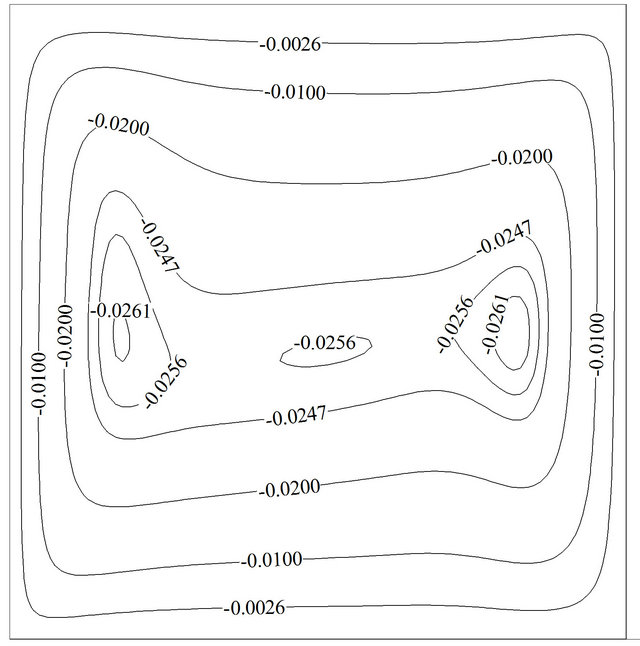 (c)
(c) (d)
(d)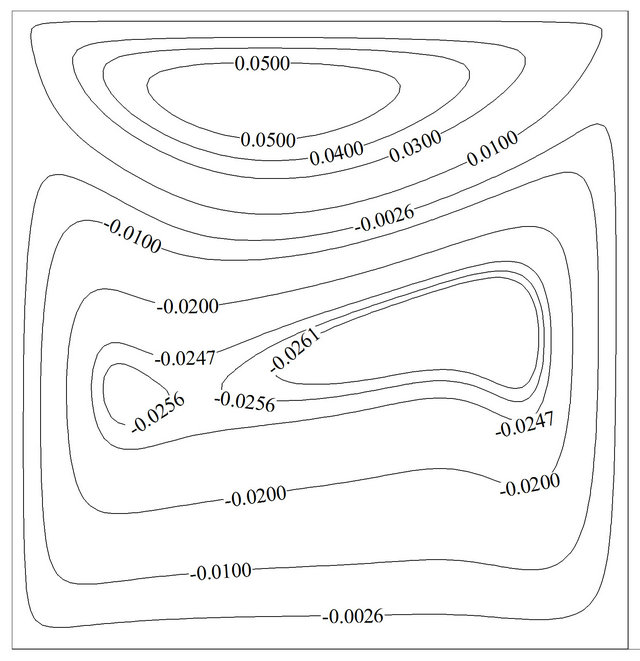 (e)
(e)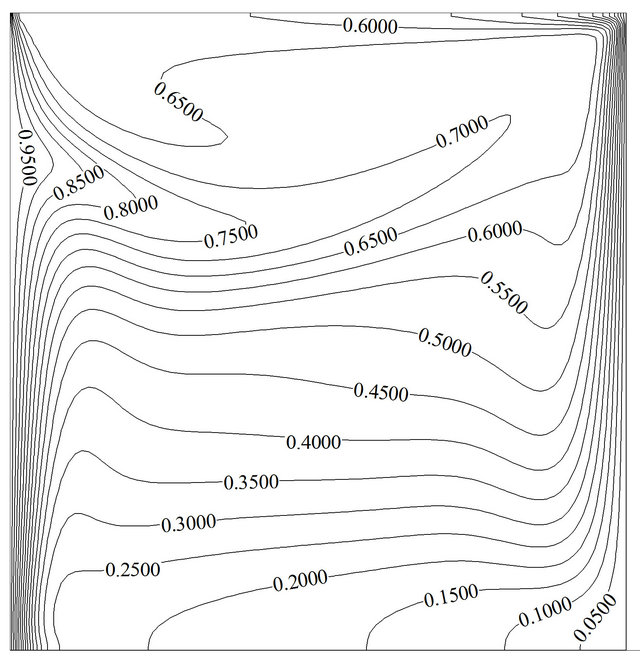 (f)
(f)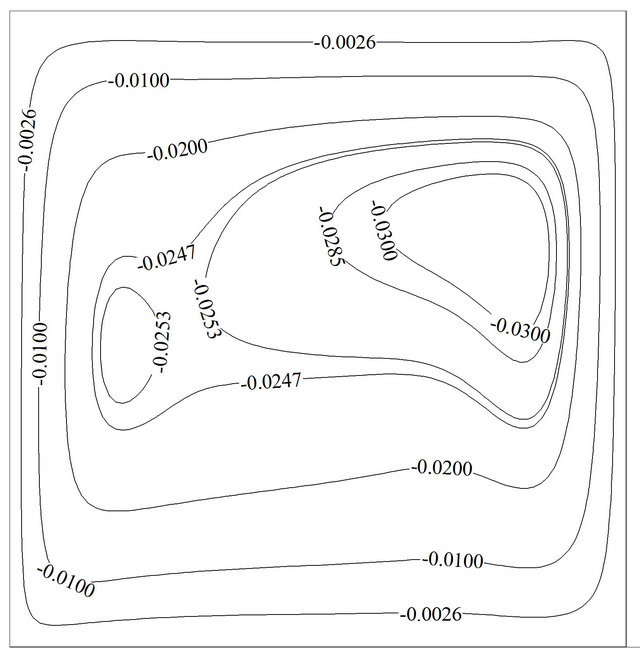 (g)
(g)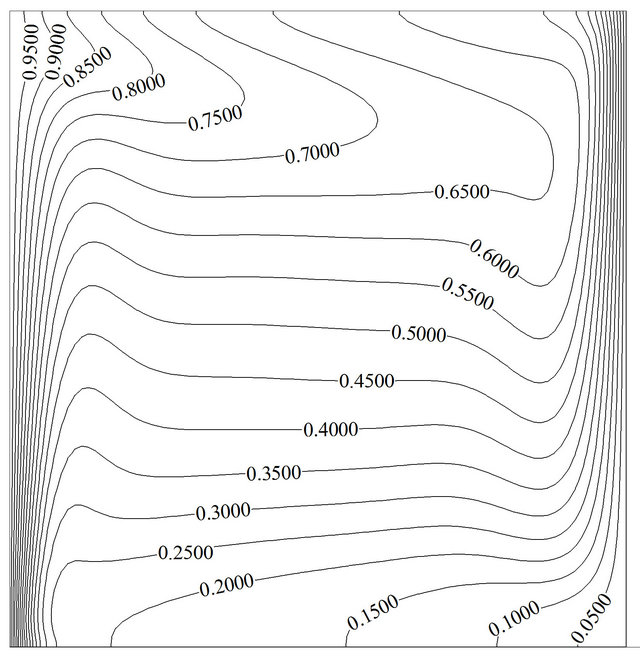 (h)
(h)
Figure 4. Variation of the streamline and isotherm contours for Re = 100, Gr = 105, Ω = π/30, f = 0%: (a) and (b) at τu = 1; (c) and (d) at τu = 0+; (e) and (f) at τu = –1; (g) and (h) at τu = 0–.
this figure streamlines and isotherms are approximately similar to the case of pure natural convection. As lid accelerates in the negative direction, the primary vortex is found to break up into two vortices and a secondary vortex appears and occupies about half of the cavity. This phenomenon disturbs the thermal boundary layer near upper parts of the hot wall and increases the average Nusselt number. A careful observation indicates that thermal boundary layer becomes thinner at upper part of the hot wall whereas the region where two vortices cannot cover (the magnitude of stream function is equal to zero), this layer will become thicker and local Nusselt number will reduce. But the overall effect is in the way of augmentation of the average Nusselt number. It should be noted that in the steady state condition the opposite behavior will be observed, in other word, the greater average Nusselt number is at u = 1 and the lesser one at u = –1 (Table 4). While negative speed value of lid becomes zero, it is expected to observe the same flow and thermal field like Figures 4(c) and (d), but Figures 4(g) and (h) shows that streamlines and isotherms are still under manipulation of negative speed value of lid due to time lapse that is needed to completely fade away the effects of the negative lid velocity inside the domain. It can be seen that the region near hot wall of the cavity can adjust itself sooner than the region near cold wall; it manifests that buoyancy force and forced convection do better and add to each other faster near hot wall.
Figure 3(b) shows the impact of variation of Reynolds number on the temporal average Nusselt number along the hot wall at Grashof number equal to 106 as well. Due to greater Grashof number, the average Nusselt number would be greater. The same behavior can be observed in Figure 3(b), but a precise observation reveals that at Re = 100, greater maximums occurs while lid has maximum positive speed value and inferior one happens at maximum negative speed value. It is true that lid negative motion disturbs thermal boundary layer near hot wall, but as Grashof number rises up, the strengthen of buoyancy force will become greater, and disturbance will be limited to rather small area near upper part of the hot wall (Figures 5(c) and (d)) and cannot heighten the Nusselt number to a great extent. In that case it can be uttered that although disturbance caused by secondary vortex can enhance heat transfer rate in general, but the vicinity impinged by this vortex is also of great importance.
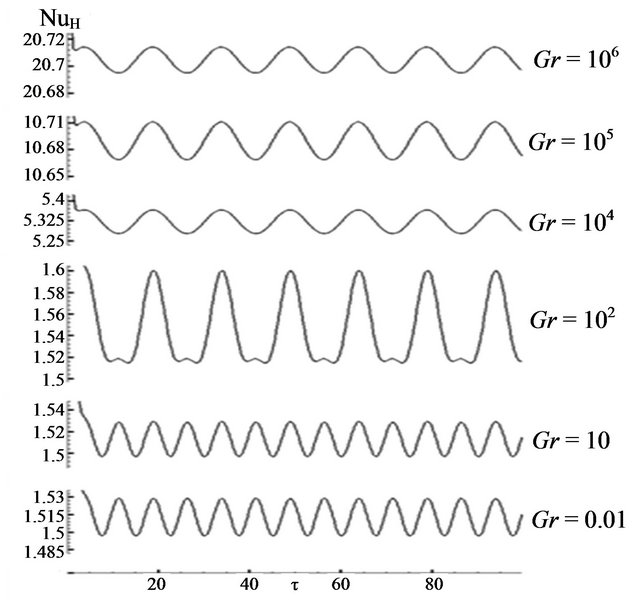
Figure 6 depicts the impact of variations of Grashof number on the temporal average Nusselt number along the hot wall while Reynolds number and non-dimensional lid frequency are fixed at 1(a), 1000(b), and π/30 respectively.
As depicted in Figure 6(a), for small values of Grashof number, flow filed is manipulated by a forced convection regime, but thermal field is under conduction dominated condition (see Figure 7). In this case thermal boundary layer is approximately independent of forced convection. It can be seen that two maximums exist in each time period that are more or less equal. This equivalence of the Nusselt number implies the fact that thermal characteristics can adjust themselves to flow field at maximum either positive or negative speed value of lid due to low Reynolds number. As Grashof number augments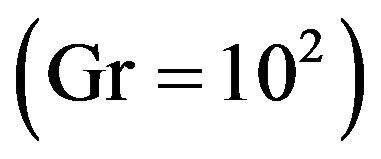 , secondary vortex will come into view. As shown, two Nusselt number maximums gradually
, secondary vortex will come into view. As shown, two Nusselt number maximums gradually
 (a)
(a)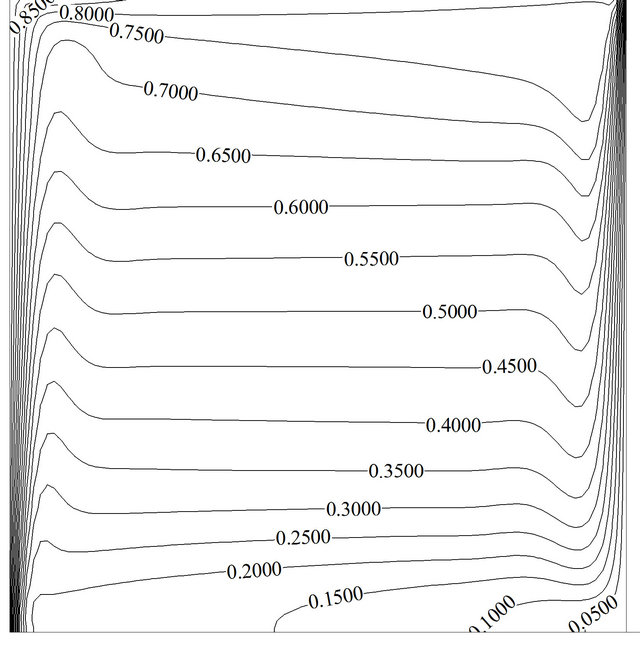 (b)
(b)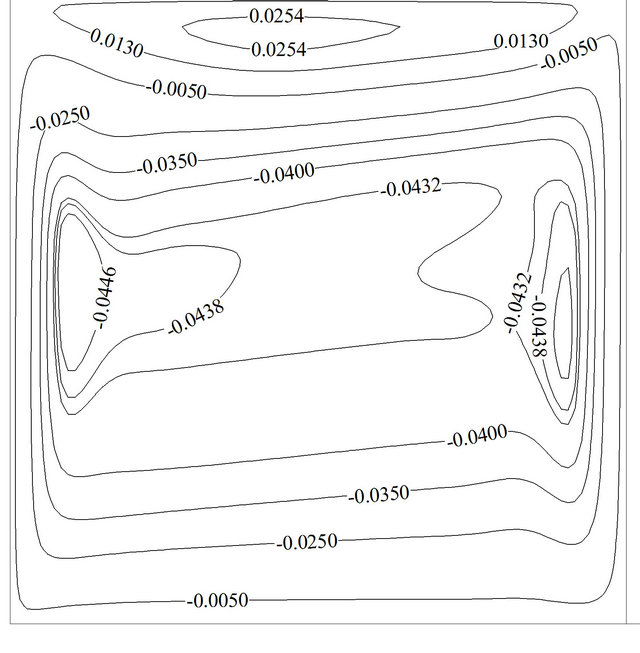 (c)
(c)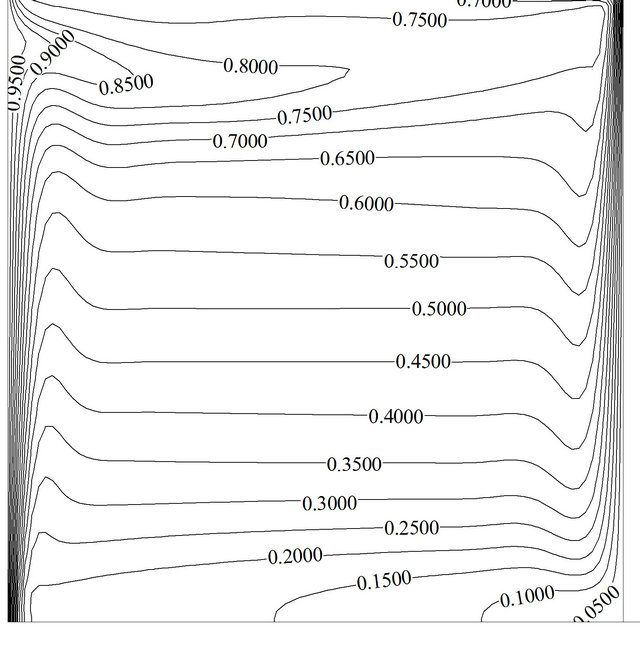 (d)
(d)
Figure 5. Variation of the streamline and isotherm contours for Re = 100, Gr = 106, Ω = π/30, f = 0%: (a) and (b) at τu = 1. (c) and (d) at τu = –1.
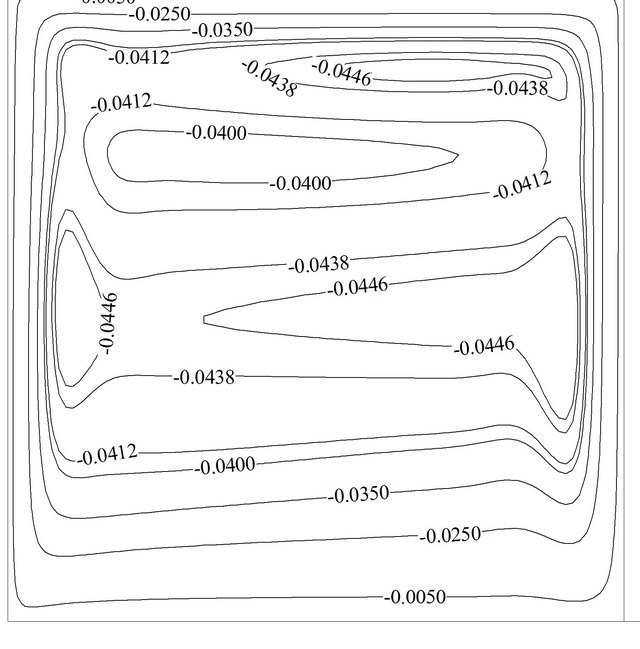
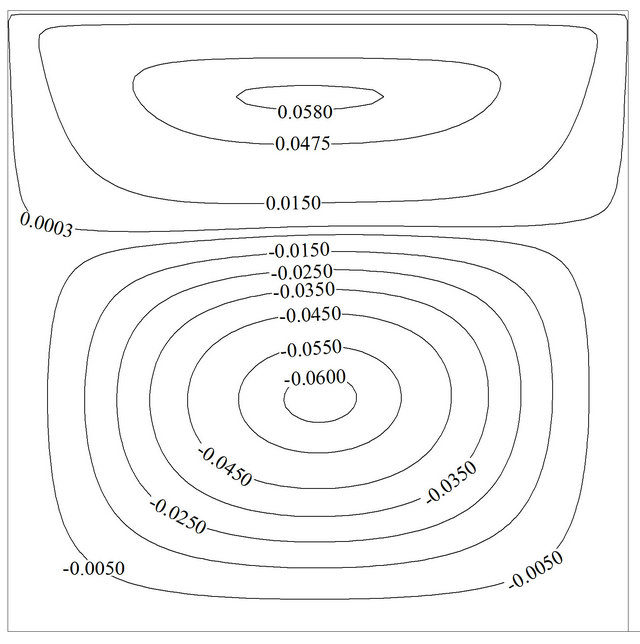
distance from each other in each time period due to emerging of secondary vortex, but there is still no disturbance on walls due to low buoyancy force. More increment of Grashof number  results in a full natural convection regime in the whole domain. In this case negative speed value of lid does not possess enough potency to generate secondary vortex. The adverse outcome of negative speed value can be seen only in negligible reduction in the average Nusselt number. For instance, at Re = 1 and Gr = 106, the differences between maximum and minimum amount of the average Nusselt number is about 0.09%. Figure 7 shows streamline and isotherm at Re = 1 and Gr = 100 while u is equal to –1.
results in a full natural convection regime in the whole domain. In this case negative speed value of lid does not possess enough potency to generate secondary vortex. The adverse outcome of negative speed value can be seen only in negligible reduction in the average Nusselt number. For instance, at Re = 1 and Gr = 106, the differences between maximum and minimum amount of the average Nusselt number is about 0.09%. Figure 7 shows streamline and isotherm at Re = 1 and Gr = 100 while u is equal to –1.
As depicted, secondary flow occupies half of the cavity, but it cannot disturb thermal boundary layer greatly due to insufficient and low inertial force, and the average Nusselt number cannot take advantage of secondary vortex so much. According to Figure 7(b) an exact look shows that at near middle part of the hot wall where two vortices meet each other, thermal boundary layer becomes thicker due to lack of fluid flow, and therefore the local Nusselt number would drop.
For high Reynolds numbers , by increasing Grashof number, we observed an overall augmentation in the average Nusselt number. According to Figure 5(b), it can be observed that at Gr = 106 and Gr = 107, the same pattern as Figure 3(b) is governed; the greater Nusselt number occurs at u = –1 and the inferior one at u
, by increasing Grashof number, we observed an overall augmentation in the average Nusselt number. According to Figure 5(b), it can be observed that at Gr = 106 and Gr = 107, the same pattern as Figure 3(b) is governed; the greater Nusselt number occurs at u = –1 and the inferior one at u
 (a)
(a)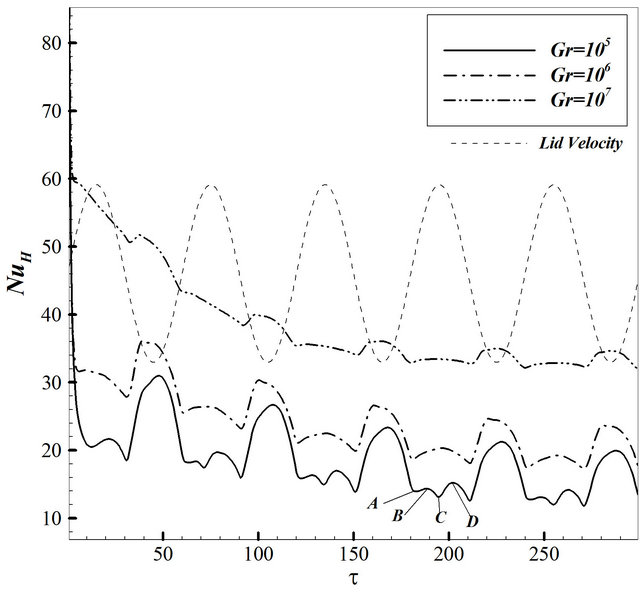 (b)
(b)
Figure 6. Variation of the average nusselt number at different grashof and reynolds numbers: (a) Re = 1, Ω = 2π/15, f = 5%; (b) Re = 1000, Ω = π/30, f = 0%.
 (a)
(a)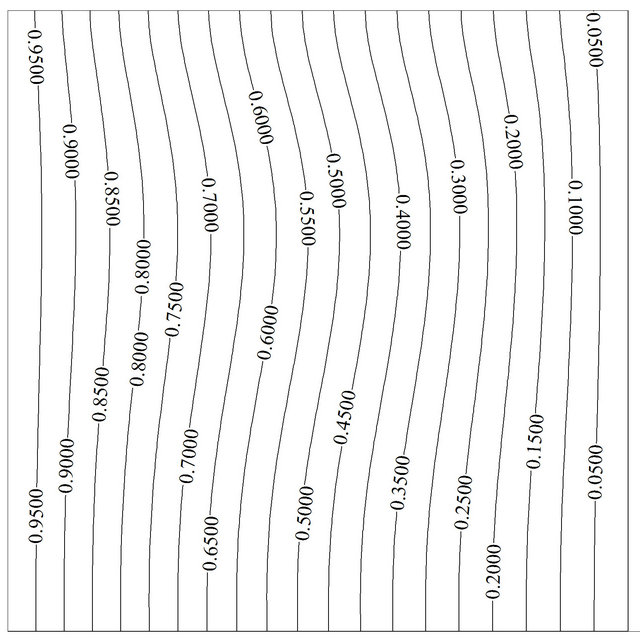 (b)
(b)
Figure 7. Variation of the (a) streamline and (b) isotherm contours for Re = 1, Gr = 102, Ω = 2π/15, f = 5% at τu = –1.
= 1. Unlike two other Grashof numbers, at Gr = 105, there are three maximums, one at u = –1, and two others occur while lid is moving in positive direction. This phenomenon can be elucidated by the fact that under this condition, forced convection and buoyancy force are in competition. As displayed in Figure 8(a), there is still a big vortex inside the cavity due to remaining negative inertia caused by lid negative motion. As lid carries on moving in positive direction, the vicinity and intensity of this vortex will diminish, but in the other hand, buoyancy force appropriates greater space and generates the second maximum Nusselt number. As lid speeds up, the seconddary vortex will be wiped out. But due to secondary vortex annihilation, and also time lag required for thermal field to adjust itself to flow field, thermal boundary layer becomes thicker at upper part of the hot wall, and results in a cut back of Nusselt number. It is worth to say again that at higher Grashof number, thermal boundary layer can adapt itself sooner, so that three maximums turn in two maximums for the Nusselt number graph.
Figure 9 shows the impact of variation of non-dimensional lid frequency on the temporal average Nusselt number on the hot wall due to fixed amount of both Reynolds and Grashof number (Re = 1,Gr = 102(a) and Re = 100, Gr = 106(b)). As illustrated in Figure 9(a), at low Reynolds number, increment of lid frequency does
 (a)
(a)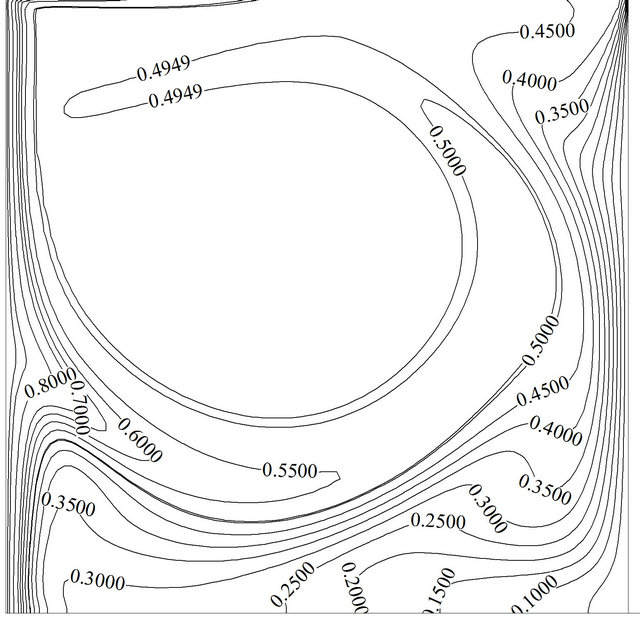 (b)
(b)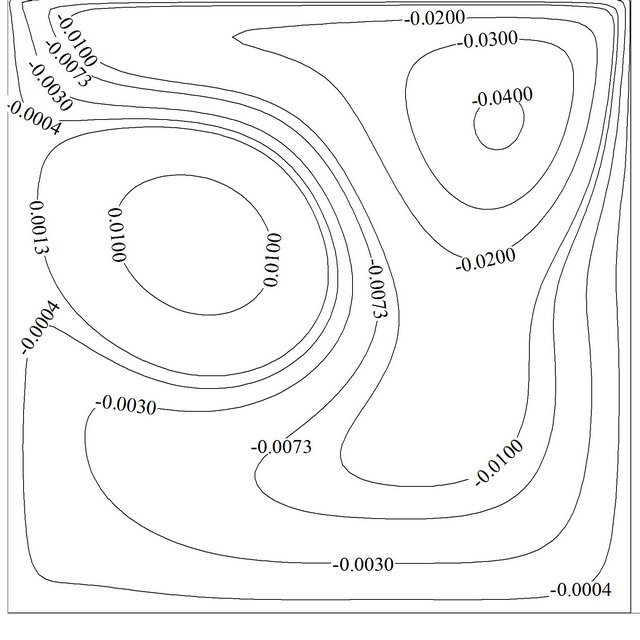 (c)
(c)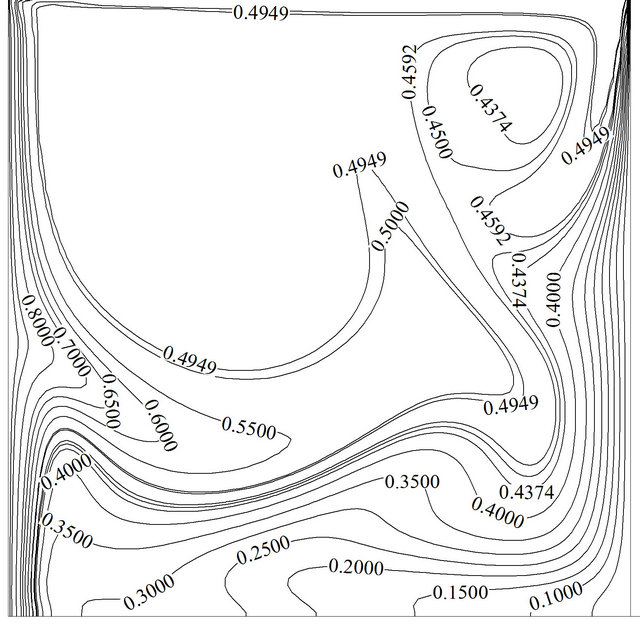 (d)
(d) (e)
(e)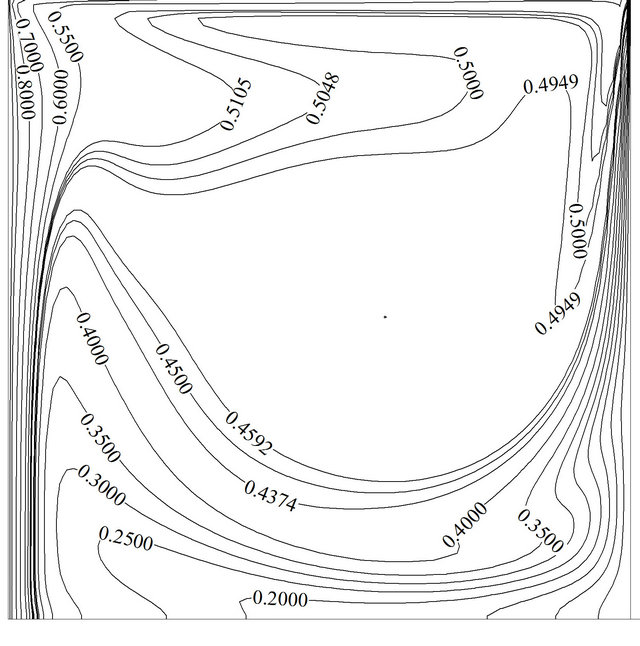 (f)
(f)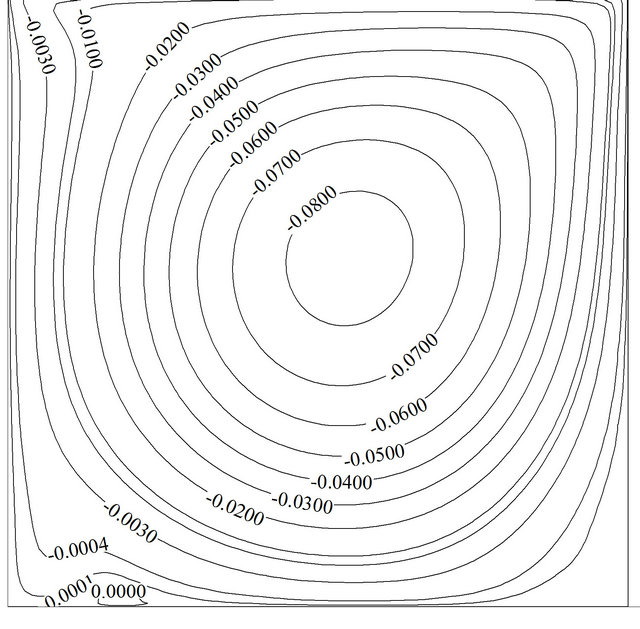 (g)
(g)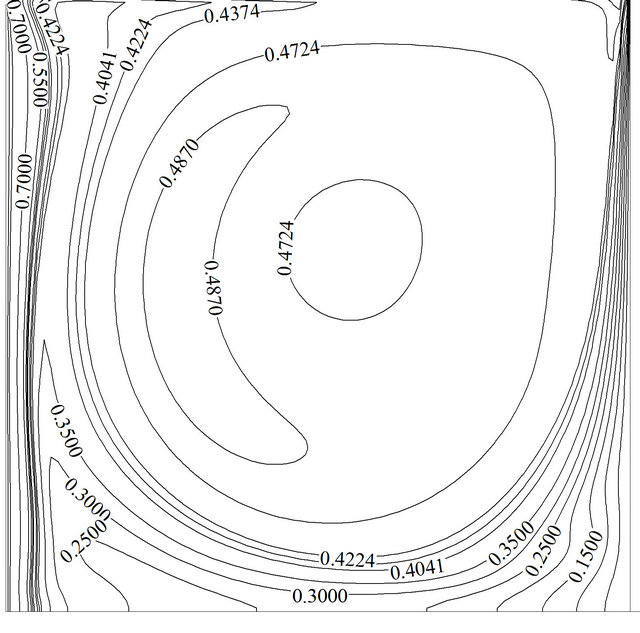 (h)
(h)
Figure 8. Variation of the streamline and isotherm contours for Re = 1000, Gr = 105, Ω = π/30, f = 0%: (a) and (b) at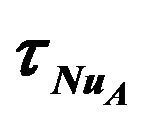 ; (c) and (d) at
; (c) and (d) at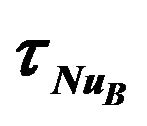 ; (e) and (f) at
; (e) and (f) at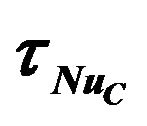 ; (g) and (h) at
; (g) and (h) at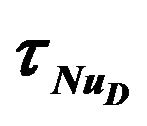 ; (Note: A, B, C, and D points are illustrated in Figure 6(b)).
; (Note: A, B, C, and D points are illustrated in Figure 6(b)).
not change the maximum and minimum amount of the Nusselt number but hastens their occurrence. In a fixed geometry, low Reynolds number denotes a fluid with high viscosity or small value of reference speed. High viscosity makes a fluid particles highly connected together, so any disturbance due to high frequencies can penetrate deeply inside the domain. On the other hand, at low speed value of lid, the inertial force of fluid is small and high frequencies cannot disturb thermal boundary layer to the point of the Nusselt number reduction. Unlike Figures 9(a) and (b) shows that by increasing frequency, the average Nusselt number drops off. This implies that the incorporation of a relatively low frequency facilitates the prevalence of forced convection over the buoyancy force. Therefore the depth of the cavity influenced by lid movement will become greater, and disturbance moving along the vertical walls can cover greater portion. This leads to a greater Nusselt number on the hot and cold walls. As frequency rises up, the buoyancy effect becomes more prominent, as it seems to confine the effectiveness of forced convection to a restricted depth of the cavity. Figure 9 also points up how swiftly the steady periodic condition is achieved for various frequencies. High frequencies cause the fluid to become motionless to a large extent in the bulk of the interior region. Therefore, heat transfer procedure becomes somewhat ineffective in this situation. This is evidently manifested on the magnitude of the predicted Nusselt number.
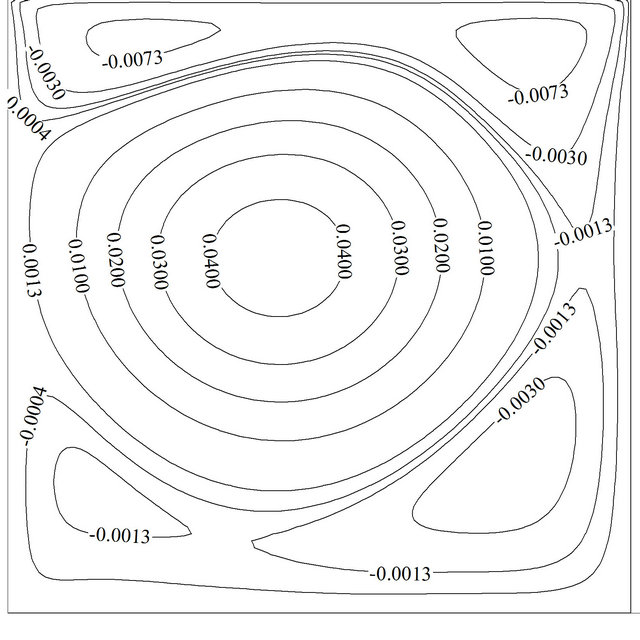
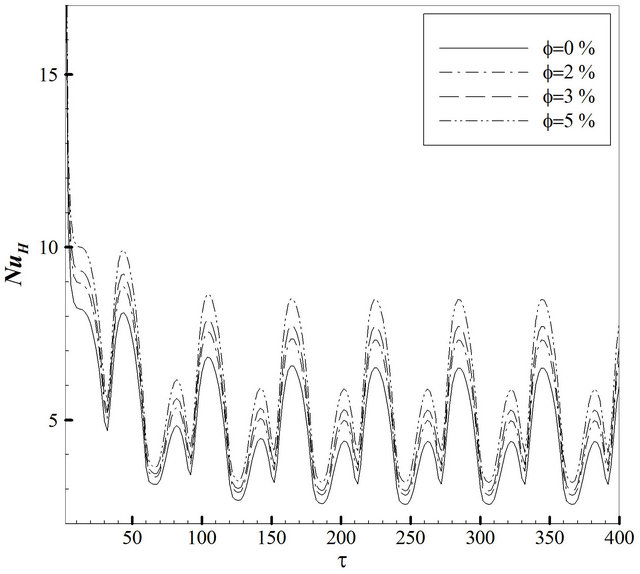
Figure 10 shows the effect of various solid volume fractions on the temporal average Nusselt number at Re = 100 and Gr = 102(a), 106(b). It is obvious that the overall effect of solid volume fraction increment is the Nusselt number augmentation. Besides, it can be seen, at higher Grashof number adding more nano-particles to base flow can be very effective rather than lower Grashof number due to higher Brownian motion velocity and higher effective thermal conductivity. So that at Re = 100, the increase of the solid concentration from 0 to 5% enhances the average Nusselt number by about 1.98 units for Gr = 102 and about 4.59 units for Gr = 106. It can be deduced that nano-particles can have better efficiency at higher temperature differences. As it is put on view in Figure 11(b), the solid volume fraction does not have impression on the flow pattern but it intensifies streamline’s values. So that the maximum value of the streamlines at Re = 100 and Gr = 106andwhile maximum Nusselt number occurs, gets from –0.0466 to –0.0576 for a 5% concentration.
6. Conclusion
An unsteady, periodic, laminar mixed-convection in a cavity utilized with copper-water nanofluid has been
 (a)
(a)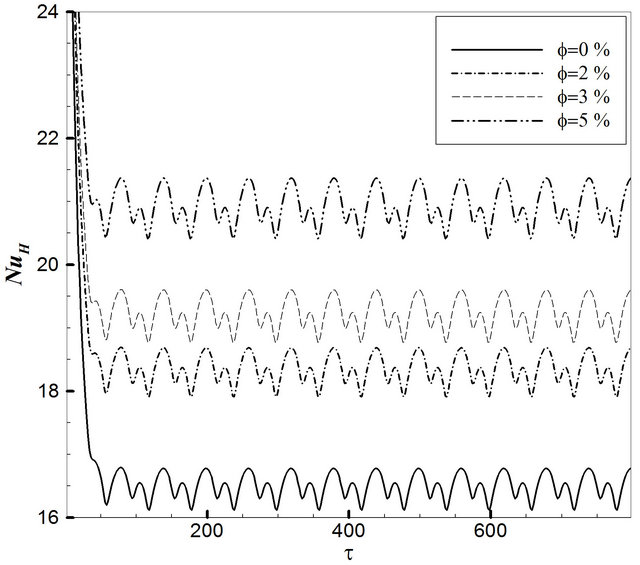 (b)
(b)
Figure 10. Variation of the average Nusselt number at various solid volume fraction: (a) Re = 100, Gr = 102, Ω = π/30; (b) Re = 100, Gr = 106, Ω = π/30.
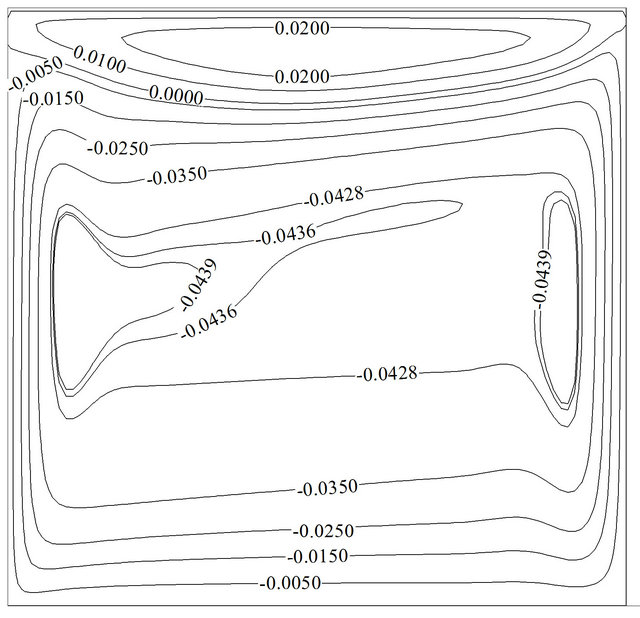
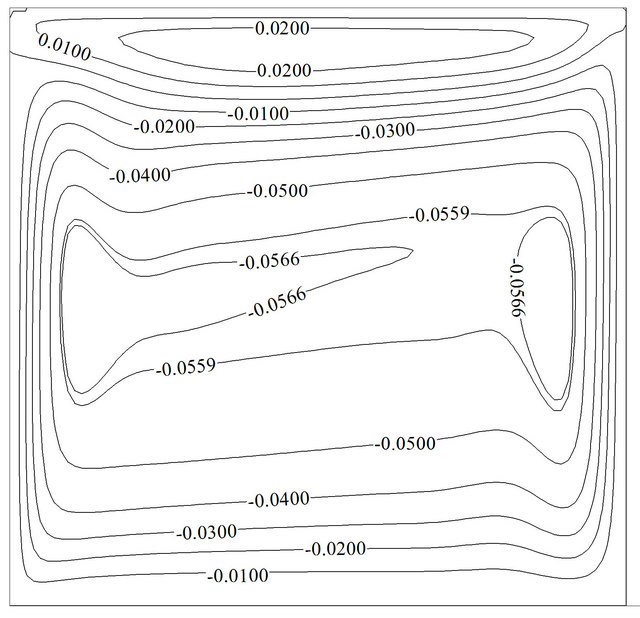
Figure 11. The effects of solid volume fraction on the streamline contours: (a) Re = 100, Gr = 106, f = 0%, τu = –1; (b) Re = 100, Gr = 106, f = 5%, τu = –1.
examined numerically. To obtain mixed-convection condition inside the cavity, upper wall of the cavity was equipped with a sliding lid, both vertical walls are subjected to constant hot and cold temperatures but two other walls assumed to be insulated. The investigation was carried out for four major parameters including Reynolds number, Grashof number, non-dimensional lid frequency, and solid volume fraction. The captured results were presented in the term of temporal average Nusselt number, streamline, and isotherm contours. Such results show that Reynolds number and Grashof number have a significant effect on the fluid flow and heat transfer fields. Actually, their effects are associated with the direction of the sliding lid. Higher average Nusselt number was observed as lid moves in the negative direction due to thermal boundary disturbance caused by seconddary vortex. Furthermore, the results reveal that the average Nusselt number predictions augment with an increase in the Reynolds number and Grashof number. It is also observed that lid frequency increment has no effect on the average Nusselt number at low Reynolds numbers but it has a dwindling effect at high Reynolds numbers due to shallower depth of lid motion penetration. Finally, more solid volume fraction will enhance heat transfer and is more effectual at high Grashof numbers.
REFERENCES
- K. Torrance, R. Davis, K. Eike, D. Gill, D. Gutman, A. Hsui, S. Lyons and H. Zien, “Cavity Flows Driven by Buoyancy and Shear,” Journal of Fluid Mechanic, Vol. 51, No. 2, 1972, pp. 221-231. doi:10.1017/S0022112072001181
- M. K. Moallemi and K. S. Jang, “Prandtl Number Effects on Laminar Mixed Convection Heat Transfer in a LidDriven Cavity,” International Journal of Heat and Mass Transfer, Vol. 35, No. 8, 1992, pp. 1881-1892. doi:10.1016/0017-9310(92)90191-T
- R. Iwatsu, J. M. Hyun and K. Kuwahara, “Mixed Convection in a Driven Cavity Witha Stable Vertical Temperature Gradient,” International Journal of Heat and Mass Transfer, Vol. 36, No. 6, 1993, pp. 1601-1608. doi:10.1016/S0017-9310(05)80069-9
- R. Iwatsu and J. M. Hyun, “Three-Dimensional DrivenCavity Flows with a Vertical Temperature Gradient,” International Journal of Heat and Mass Transfer, Vol. 38, No. 18, 1995, pp. 3319-3328. doi:10.1016/0017-9310(95)00080-S
- L. Martinez-Suastegui, C. Trevino and F. Mendez, “Natural Convection in a Vertical Strip Immersed in a Porous Medium,” European Journal of Mechanics B/Fluids, Vol. 22, No. 6, 2003, pp. 545-553. doi:10.1016/j.euromechflu.2003.08.003
- Q. G. Xiong, B. Li, F. G. Chen, J. S. Ma, W. Ge and J. H. Li, “Direct Numerical Simulation of Sub-Grid Structures in Gas-Solid Flow-GPU Implementation of Macro-Scale Peudo-Particle Modeling,” Chemical Engineering Science, Vol. 65, No. 19, 2010, pp. 5356-5365. doi:10.1016/j.ces.2010.06.035
- Q. G. Xiong, B. Li and J. Xu, “GPU-Accelerated Adaptive Particle Splitting and Merging in SPH,” Computer Physics Communications, Vol. 184, No. 7, 2013, pp. 1701-1707. doi:10.1016/j.cpc.2013.02.021
- Q. G. Xiong, B. Li, G. F. Zhou, X. J. Fang, J. Xu, J. W. Wang, X. F. He, X. W. Wang, L. M. Wang, W. Ge and J. H. Li, “Large-Scale DNS of Gas-Solid Flows on Mole- 8.5,” Chemical Engineering Science, Vol. 71, 2012, pp. 422-430. doi:10.1016/j.ces.2011.10.059
- H. Shokouhmand, S. M. A. Noori Rahim Abadi and A. Jafari, “The Effect of the Horizontal Vibrations on Natural Heat Transfer from an Isothermal Array of Cylinders,” International Journal of Mechanics and Materials in Design, Vol. 7, No. 4, 2011, pp. 313-326.
- H. Shokouhmand, S. M. A. Noori Rahim Abadi and A. Jafari, “Finite Element Analysis of Heat Transfer within a Square Cavity with Uniform and Nonuniform Boundary Heating,” Heat Transfer Research, Vol. 42, No. 4, 2011, pp. 337-358.
- F. J. K. Ideriah, “Prediction of Turbulent Cavity Flow Driven by Buoyancy and Shear,” Journal of Mechanical Engineering Science, Vol. 22, No. 6, 1980, pp. 287-295. doi:10.1243/JMES_JOUR_1980_022_054_02
- C. K. Cha and Y. Jaluria, “Recirculating Mixed Convection Flow for Energy Extraction,” International Journal of Heat and Mass Transfer, Vol. 27, No. 10, 1984, pp. 1801-1810. doi:10.1016/0017-9310(84)90162-5
- G. De Vahl Davis, “Natural Convection in Air in a Square Cavity: A Bench Mark Numerical Solution,” International Journal for Numerical Methods in Fluids, Vol. 3, No. 3, 1983, pp. 249-264. doi:10.1002/fld.1650030305
- T. Fusegi, J. M. Hyun and K. Kuwahara, “Numerical Study of Natural Convection in a Differentially Heated Cavity with Internal Heat Generation: Effects of the Aspect Ratio,” Journal of Heat Transfer, Vol. 114, No. 3, 1992, pp. 773-778. doi:10.1115/1.2911350
- H. F. Oztop, E. Abu-Nada, Y. Varol and A. Chamkha, “Natural Convection in Wavy Enclosures with Volumetric Heat Sources,” International Journal of Thermal Sciences, Vol. 50, No. 4, 2010, pp. 502-514.
- M. K. Moallemi and K. S. Jang, “Prandtl Number Effects on Laminar Mixed Convection Heat Transfer in a LidDriven Cavity,” International Journal of Heat and Mass Transfer, Vol. 35, No. 8, 1992, pp. 1881-1892. doi:10.1016/0017-9310(92)90191-T
- M. A. R. Sharif, “Laminar Mixed Convection in Shallow Inclined Driven Cavities with Hot Moving Lid on Top and Cooled From Bottom,” Applied Thermal Engineering, Vol. 27, No. 5-6, 2007, pp. 1036-1042. doi:10.1016/j.applthermaleng.2006.07.035
- H. F. Oztop and I. Dagtekin, “Mixed Convection in Two-Sided Lid-Driven Differentially Heated Square Cavity,” International Journal of Heat and Mass Transfer, Vol. 47, No. 8-9, 2004, pp. 1761-1769. doi:10.1016/j.ijheatmasstransfer.2003.10.016
- Y. Varol, H. F. Oztop and I. Pop, “Natural Convection in a Diagonally Divided Square Cavity Filled with a Porous Medium,” International Journal of Thermal Sciences, Vol. 48, No. 7, 2009, pp. 1405-1415. doi:10.1016/j.ijthermalsci.2008.12.015
- S. Sivasankaran, V. Sivakumar and P. Prakash, “Numerical Study on Mixed Convection in a Lid-Driven Cavity with Non-Uniformheating on Both Sidewalls,” International Journal of Heat and Mass Transfer, Vol. 53, No. 19-20, 2010, pp. 4304-4315. doi:10.1016/j.ijheatmasstransfer.2010.05.059
- T. Nishimura and K. Kunitsugu, “Fluid Mixing and Mass Transfer in Two-Dimensional Cavities with Time-Periodic Lid Velocity,” International Journal of Heat and Fluid Flow, Vol. 18, No. 5, 1997, pp. 497-506.
- W. H. Soh and J. W. Goodrich, “Unsteady Solution of Incompressible Navier-Stokes Equations,” Journal of Computational Physics, Vol. 79, No. 1, 1988, pp. 113- 134. doi:10.1016/0021-9991(88)90007-1
- R. Iwatsu, J. M. Hyun and K. Kuwahara, “Numerical Simulation of Flows Driven by a Torsionally Oscillating Lid in a Square Cavity,” Journal of Fluids Engineering, Vol. 114, No. 2, 1992, pp. 143-151. doi:10.1115/1.2910008
- R. Iwatsu, J. M. Hyun and K. Kuwahara, “Convection in a Differentially-Heated Square Cavity with AtorsionallyOscillating Lid,” International Journal of Heat and Mass Transfer, Vol. 35, No. 5, 1992, pp. 1069-1076. doi:10.1016/0017-9310(92)90167-Q
- K. M. Khanafer, A. M. Al-Amiri and I. Pop, “Numerical Simulation of Unsteady Mixed Convection in a Driven Cavity Using an Externally Excited Sliding Lid,” European Journal of Mechanics B/Fluids, Vol. 26, No. 5, 2007, pp. 669-687. doi:10.1016/j.euromechflu.2006.06.006
- H. T. Zhu, Y. S. Lin and Y. S. Yin, “A Novel One-Step Chemical Method for Preparation of Copper Nanofluids,” Journal of Colloid and Interface Science, Vol. 277, No. 1, 2004, pp. 100-103. doi:10.1016/j.jcis.2004.04.026
- S. M. Aminossadati and B. Ghasemi, “Natural Convection Cooling of a Localized Heat Source at the Bottom of a Nanofluid-Filled Enclosure,” European Journal of Mechanics B/Fluids, Vol. 28, No. 5, 2009, pp. 630-640. doi:10.1016/j.euromechflu.2009.05.006
- X. Wang, X. Xu and S. U. S. Choi, “Thermal Conductivity of Nanoparticle-Fluid Mixture,” Journal of Thermophysics and Heat Transfer, Vol. 13, No. 4, 1999, pp. 474- 480. doi:10.2514/2.6486
- K. Khanafer, K. Vafai and M. Lightstone, “BuoyancyDriven Heat Transfer Enhance Mentin a Two-Dimensional Enclosure Utilizing Nanofluids,” International Journal of Heat and Mass Transfer, Vol. 46, No. 19, 2003, pp. 3639-3653. doi:10.1016/S0017-9310(03)00156-X
- A. H. Mahmoudi, M. Shahi, A. M. Shahedin and N. Hemati, “Numerical Modeling of Natural Convection in an Open Cavity with Two Vertical Thin Heat Sources Subjected to a Nanofluid,” International Communications in Heat and Mass Transfer, Vol. 38, No. 1, 2010, pp. 110- 118. doi:10.1016/j.icheatmasstransfer.2010.09.009
- H. C. Brinkman, “The Viscosity of Concentrated Suspensions and Solutions,” The Journal of Chemical Physics, Vol. 20, No. 4, 1952, pp. 571-581.
- H. E. Patel, T. Pradeep, T. Sundararajan, A. Dasgupta, N. Dasgupta and S. K. Das, “A Micro Convection Model for Thermal Conductivity of Nanofluid, Pramana,” Journal of Physics, Vol. 65, No. 5, 2005, pp. 863-869.
- H. Kumar, D. Patel, E. Hrishikesh, V. R. Rajeev Kumar, T. Sundararajan, T. Pradeep and S. K. Das, “Model for Heat Conduction in Nanofluids,” Physical Review Letters, Vol. 93, No. 14, 2004, pp. 144301-1-4
- P. Keblinski, S. R. Phillpot, S. U. S. Choi and J. A. Eastman, “Mechanisms of Heat Flow in Suspensions of NanoSized Particles (Nanofluids),” International Journal of Heat and Mass Transfer, Vol. 45, No. 4, 2002, pp. 855- 863. doi:10.1016/S0017-9310(01)00175-2
- N. Massarotti, P. Nithiarasu and O. C. Zienkiewicz, “Characteristic Based Split (CBS) Algorithmfor Incompressible Flow Problems with Heat Transfer,” International Journal of Numerical Methods for Heat & Fluid Flow, Vol. 8, No. 8, 1998, pp. 969-990. doi:10.1108/09615539810244067
- F. Talebi, A. H. Mahmoudi and M. Shahi, “Numerical Study of Mixed Convection Flows in a Square LidDriven Cavity Utilizing Nanofluid,” International Communications in Heat and Mass Transfer, Vol. 37, No. 1, 2010, pp. 79-90. doi:10.1016/j.icheatmasstransfer.2009.08.013
Nomenclature

NOTES
*Corresponding author.

