Advances in Materials Physics and Chemistry
Vol.05 No.03(2015), Article ID:54501,35 pages
10.4236/ampc.2015.53013
Physical Properties of Some Stoichiometric Rare Earth Nitride Single Crystals
Peter Wachter
Laboratorium für Festkörperphysik, ETH Zürich, Zürich, Switzerland
Email: wachter@solid.phys.ethz.ch
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 January 2015; accepted 6 March 2015; published 10 March 2015
ABSTRACT
The preparation and definition of large (3 - 5 mm edge length) single crystals of ScN, GdN, TbN, HoN, YbN and CeN is described. The Hall effect and the electrical conductivity are found to be me- tallic. The optical reflectivity between 30 meV (sometimes 1 meV) and 13 eV has been measured and the dielectric functions have been obtained. A plasma edge in the infrared confirms the metal- lic character. In GdN, a shift of this plasma edge with temperature through the magnetic ordering temperature has been observed as a new effect. GdN is in low magnetic fields antiferromagnetic, but becomes ferromagnetic in larger fields. The band structure is discussed. The magnetic ex- change interactions have been derived. HoN in the relevant crystal directions has a spontaneous magnetic moment, but no saturation in fields up to 10 T. CeN is intermediate valent and exhibits a Pauli paramagnetism. The specific heat is measured down to 0.3 K and an enhanced g value is ob- served.
Keywords:
Crystal Growth, Electrical Properties, XPS, BIS, Optical Properties, Magnetic Properties

1. Introduction
After the discovery of the first ferromagnetic semiconductor EuO by Matthias, Bozorth and van Vleck [1] , the search for other ferromagnetic semiconductors was getting stronger. The rare earth pnictides are obvious candi- dates since III-V materials generally are semiconductors like AlN, GaN, GaAs and InSb (going from large gap to narrow gap semiconductors) and rare earths have generally magnetic ions. An advantage is that all rare earth pnictides crystallize in the simple rock-salt structure and can be mixed amongst each other.
Whereas, the well-known III-V compounds mentioned above are all semiconductors or insulators, rare earth pnictides are all metallic, as judged from the temperature dependence of the n-type electrical resistivity. Very early, the question arose why this might be the case. When the composition of the compounds had been investi- gated in rare cases, one always observed metal excess and of course the metal ions donated excess free electrons causing the metallic character. So, is the whole story a problem of non-stoichiometry? For 20 years or so one tried to make the compounds more stoichiometric, for phosphides, arsenides and antimonides with limited suc- cess, but for nitrides without success.
In this laboratory, methods to determine the nitrogen content of rare earth compounds had to be developed, the so called Kjeldahl method, and been brought to a precision of ±0.5%. The trained personal and the special equipment raised enormous costs during some years. But then we were successful with stoichiometric polycrys- talline samples.
To grow single crystals with melting points of about 2000˚C is another story of success. Closed crucibles of tungsten were necessary and each crucible was broken to retrieve the crystals. In the course of time, about 10,000 crucibles had been consumed (not only for rare earth nitrides, but also for chalcogenides). The growth of stoichiometric rare earth nitrides brought crystal growth to new levels.
Today non-stoichiometric rare earth nitrides can also be grown as thin films by shooting charged nitrogen ions onto rare earth metallic films and thus produce even excess nitrogen and p-type conductivity. Now, the samples can be semiconductors and sometimes ferromagnetic. The old dream of a new ferromagnetic semicon- ductor is thus revived.
The rare earth pnictides except the nitrides can be prepared quite easily and even single crystals can be grown in closed crucibles of boron nitride, molybdenum or tungsten at temperatures near 2000 K (we refer to Hand- book articles of Hulliger [2] and Vogt and Mattenberger [3] [4] .
Stoichiometry (from Greek stoiceionmetrein basic material measure) is the key element for all rare earth pnictides, but especially for the nitrides. Exact stoichiometry means e.g. Gd1.0N1.0, but all pnictides generally have metal excess up to 10%, e.g. Gd1.0N0.9 or Gd1.1N1.0. As will be more elaborated later on, each excess metal ion will donate excess electrons and turn a possible semiconductor into a semimetal or metal. The magnetic in- teractions are at least composed of two parts―an indirect super-exchange involving bonding and anti-bonding d-orbits of the cation and the p orbits of the anion―and a RKKY type interaction where the oscillatory beha- viour depends on the carrier concentration. Thus a stoichiometric nitride may be an antiferromagnet, but be- comes a ferromagnet with off-stoichiometry. In this paper we use the term stoichiometry in short for a 1:1 exact stoichiometry, else wise we use the term off-stoichiometry.
Very often, it is the crystal structure and rock-salt phase purity, which is used as a sign of stoichiometry. Even in the most recent investigation on rare earth nitrides by Hirayama et al. [5] the phase purity from XRD (X-Ray Diffraction) has been used to claim perfect stoichiometric polycrystalline samples. But it is a fact that non-stoi- chiometry up to 10% is still single phase with only the rock-salt structure. Of course there is a large diffuse background since the lattice defects are disordered and do not exhibit another crystallographic phase. But when one insists on using 99.99% pure rare earths and 99.9995% pure N and thus hoping to get perfect samples one has not understood the problems with non-stoichiometry (Hirayama et al. [6] ). Some authors realize or even measure the off-stoichiometry of their samples but think a small misfit would not change the physics of the ma- terial. But it does, as will be shown further down. So Child et al. [6] measured about 95% nitrogen and Sclar [7] about 90% with the Kjeldahl method.
All rare earth nitrides are metallic conducting (the other pnictides just as well) when measured in function of temperature. The point is: are they metallic because of excess electrons due to non-stoichiometry or is this an in- trinsic property due to the band structure and p-d overlap? In any case those nitrides, which have the lowest car- rier concentration and perfect measured stoichiometry are the best and serve as intrinsic standards.
2. Materials and Methods
Historically the preparation of nitrides was via heating the metal in flowing nitrogen [8] , or to produce hydrides [6] or amalgams [9] , which were converted with NH3 to nitrides. Whereas the former all yield polycrystalline powders of various compositions, single crystals of the nitrides can also be grown [10] [11] . In short, the han- dling of the metal and the compound has been performed in metallic argon glove boxes gettered by hot cerium turnings, having a residual oxygen concentration of less than 3 ppm. Commercially available 99.99% sublimed rare earth metal has been transformed into metal turnings in the glove boxes and pre-reacted with an induction furnace in an open Mo crucible for 12 h at 1900˚C in a nitrogen stream. The resulting polycrystalline material has been reground in the glove box and nitrified again for 12 h and the procedure repeated again. Even after 24 h of X-ray irradiation only the rock-salt structure could be detected. The material has been analyzed with a micro Kjeldahl method [11] for its nitrogen content and was found to be stoichiometric (±0.5%). This pre-reacted ma- terial has been put into a tungsten crucible closed and welded with an electron beam. A temperature gradient of 1940˚C and 1970˚C between top and bottom of the crucible has been maintained for 11 days and then the cruci- ble has been slowly cooled. Large single crystals between 3 mm and 5 mm edge length had grown. Within the precision of the chemical analysis no nitrogen has been lost. Single crystals from this crucible have been cleaved in the glove box and been transferred without contamination with air into the various measuring apparatuses. Single crystals from top or bottom of the crucibles, though with the same stoichiometry, could have slightly different physical properties, so all physical measurements should be done on the very same single crystal.
The perfection and quality of the rare earth nitrides is extremely important. As band structure calculations show (see below) there is an indirect overlap between the p-band of nitrogen and the d band of the rare earth. This overlap can be of only meV energy and thus the intrinsic carrier concentration is in the order of percent. A change in stoichiometry of only 1% may change the carrier concentration by 100% and thus influence all physical parameters like lattice constant, magnetic and optical properties and electric conductivity,
A simple test of the perfection of the nitride material is to leave a polycrystalline sample over night on the table in the laboratory. On the next morning an originally non-stoichiometric black powder has become a white material, e.g. Gd2O3 or Gd(OH)3. Instead a stoichiometric single crystal could be boiled for hours in a mixture of HNO3 and H2SO4 before being dissolved.
In this paper, we want to compare and measure physical properties of interesting rare earth nitrides, stoichio- metry tested (Kjeldahl), large single crystals (ScN, GdN, TbN, HoN, YbN, CeN) and relate them to earlier mea- sured results on non-stoichiometric, polycrystalline samples. The results are drastically different.
3. Band Structure
Band structure calculations have made great progress in the last years. But it is still a problem to treat localized 4f and itinerant p or d bands on the same level. Actually, the first band structure calculation for a rare earth material, EuS, a ferromagnetic semiconductor, has been performed by Cho [12] , a scholar of Slater. He used the APW method (Augmented Plane Wave), meaning that the localized 4f have been treated as plane waves and consequently ended up with a 4f band-width of 0.5 eV. The position of this band within the other p, d and s bands has been taken from experiments [13] [14] . But in reality the 4f7 state in the Eu chalcogenides and Gd pnictides is only about less than 10−4 eV [15] wide. This value has been obtained on a Gd doped LaSb single crystal using ESR with 34.7 GHz. Divalent Eu and trivalent Gd have the same ground state 8S7/2. In a magnetic field, the degeneracy of the S state is lifted and ESR oscillations for the seven DM = 1 levels of Gd can be observed. Today the Density Functional Theory DFT [16] for materials containing both localized and itinerant electrons using a Self-Interaction Corrected Local-Spin-Density (SIC-LSD) energy functional seems to work better and the electronic structure of the rare earth nitrides within the pnictides and chalcogenides has been calculated. The essential statement is that most rare earth nitrides are semiconductors, which is at variance with the experimental findings on stoichiometric single crystals, which all indicate semimetallic behaviour and metallic electrical conductivity (see below). But in the calculation “the localized 4f’s cannot be expressed [16] since the SIC-LSD approach, which after all is a one electron ground state theory, does not give accurate removal energies of localized many electron states due to electron-electron interaction effects and the neglect of screening and relaxation contributions”, literal quotation of Ref. 16. So there are still problems with even modern band structure calculations.
It is thus reasonable to start band structure calculation with a non-rare earth nitride, which serves as a reference material. For this purpose ScN is ideal, better still as LaN.
ScN is a non-4f material, so standard band structure calculations [17] are feasible using the Local Density Approximation LDA [18] . The resulting band structure is shown in Figure 1. The maximum of the p valence band is a threefold degenerate G15 level and the dt2g conduction band has three equivalent anisotropic minima at the X point of the Brillouin zone. This band structure, except for the 4f levels, holds for practically all rare earth pnictides and it shows already the problems of the whole field. The p bands at G and the d bands at X can have a slight indirect overlap of only meV energy, making the material a self compensated semimetal with equal numbers of electrons and holes, otherwise a small meV indirect gap may result between p and d bands, making the material a low gap semiconductor. The precision of the band structure calculation probably does not reach the
Figure 1. Self consistent band structure of ScN (Ref. 18).
meV level, so experiments must decide with their problems of preparing stoichiometric single crystals as described above. Nevertheless the band structure calculation [18] for ScN yields a negative indirect gap for G-X of ?6 mRy or −80 meV making the material a semimetal in agreement with experimental findings [19] [20] .
4. ScN
ScN single crystals with about 3 mm edge length have been grown with the above method and precautions and have been chemically analyzed to be ScN0.99. The lattice constant was 4.502 Å with the rock-salt structure only. The following measurements have all been made on the same single crystal. The electrical conductivity sdc = 2.44 × 104 (Wcm)−1 at 300 K with a negative temperature gradient, i.e. metallic. Sclar [7] was the first to measure the electrical resistivity on sintered polycrystalline non-stoichiometric ScN. The 300 K resistivity was higher than our value above due to inter-grain resistance and partial conversion to the insulator oxide [7] . But the temperature coefficient of resistance was positive, i.e. also metallic. The n-type Hall effect of our single crystals yields n = 5.9 × 1020 cm−3 which results in n/Sc = 0.013. The carrier concentration n is in good agreement with Ref. 19 who finds a range between 1020 and 1021 cm−3. The mobility m from s = e n m is equal to 260 cm2/Vsec. In spite of the fact that the carrier concentration n is with about 1% per ion extremely low, ScN could not be driven into p-conductivity [19] , so the material is not a degenerate semiconductor, but the carrier concentration comes from the intrinsic indirect overlap of the p band at G with the dt2g band at X (see Figure 1) [18] , which makes it a semimetal. The surprising high mobility for an ionic (50% ionic character after Pauling) nitride is of course due to the absence of 4f scattering centres. Because of the indirect overlap of p and d band at G and X we have a self compensated semimetal with heavy holes and light holes in the p band and electrons in the d band. Because the Hall effect is negative the electrons are dominant. But we must realize that the electrical conductivity, the Hall effect and mobility are average values over all carriers.
Optical properties have been measured by many authors, but usually only in limited spectral ranges. Sclar [7] was the first to measure transmission on thin films of several nitrides and claimed absorption edges and gaps around 2 eV. But his spectral range ended at 0.5 eV, so he missed the plasma edges of the materials in the infrared and claimed the nitrides to be large gap semiconductors. But he probably measured the direct gap inter-band transition p-d at G (see Figure 1) as absorption edge and left the reader with the contradiction of metallic resistivity and large gap semiconductors. Dismukes et al. [21] measured the absorption coefficient of ScN between 0.8 and 2.25 eV. He found a free carrier absorption and claimed an inter-band transition at 1.85 eV. Wachter [22] measured the optical reemission on poly-crystalline and non-stoichiometric nitrides and observed absorption minima between the plasma edge and inter-band transitions around 1 eV. This is reasonable for non-stoichi- ometric powders, since even Harbeke et al. [19] found on nearly stoichiometric ScN films these minima at about 0.5 eV. But else wise also they had a very limited spectral range between only 0.1 and 1 eV [19] .
The situation needed clarification and so we measured the reflectivity of the ScN cleaved or polished single crystal with four spectrometers from 1 meV to 12 eV spectral range at 300 K, more than 4 orders of photon energy [20] . A partial view of the reflectivity is shown in Figure 2(a) and in the low energy range in Figure 2(b). The large experimental photon range permitted simple and standard extrapolations towards larger energies and to w®0, so that a Kramers-Kronig (KK) transformation was possible with great precision [20] and all dielectric functions could be displayed. In Figure 3, we show the real and imaginary part of the dielectric function and we clearly see the free carrier absorption (Drude like) and inter-band transitions. These transitions are found that when grad E (k) of initial and final state of the transition are identical, typically between maxima and minima of the band structure, but not only. Also the same slope may result in a transition. The absorptive part e2 shows as lowest energy inter-band transition a peak at 0.8 eV, corresponding to the direct transition p-d at X in Figure 1. The next peak in e2 is at 2.7 eV, corresponding to the direct transition p-d at G in Figure 1. The energy of these transitions is exactly reproduced in Figure 1, but none of the previous authors claiming to have seen inter-band transitions have these values [7] [19] - [22] . The next peak in e2 is at 3.5 eV and corresponds to p-6s at G. The next peak in e2 at 5.5 eV probably corresponds to a p-d transition between G and the d-maximum between G and K, the next peak in e2 is at 6.2 eV and corresponds to p-d at L. The peak at 7.2 eV corresponds to p-d between Gand K. And finally, the peak in e2 at 8 eV corresponds also to p-d at L. In the author’s opinion there has never been such a close relationship between band structure calculation [18] and experimental transitions stemming from a KK transformation of optical reflectivity [20] .
In Figure 4 and Figure 5, we show the imaginary part and the real part of the dielectric function, respectively, in an expanded energy scale in the far infrared. In these figures we can see other important contributions to e2, namely the TO phonons and the Drude term of the free carriers. It produces the sharp plasma minimum in Figure 2(a) and Figure 3 at 0.4 eV, corresponding to a screened plasma resonance of wpo/(eopt)1/2. eopt could be determined to be 5.2, approximately seen in Figure 3, but exactly given by e1 outside the shown spectral range.

Figure 2. (a) Reflectivity of ScN between 5 meV and 12 eV (20); (b) Details of the reflectivity of ScN in the far infrared (20).
Figure 3. Real (ε1) and imaginary (ε2) dielectric functions of ScN (20).
Figure 4. ε2 of ScN in the far infrared and its decomposition into a phonon part, a Drude part and interband transitions (20).
Figure 5. ε1 of ScN in the far infrared and its decomposition into a phonon part, a Drude part and interband transitions (20).
This value is about half as much as in Ref. 19 where a value of 10.8 has been quoted due to their limited spectral range. The unscreened plasma resonance wpo is found near 0.99 eV.
In Ref. 20, a detailed analysis of the effective masses with heavy and light holes in the p band and optical masses of an electron hole pair has been carried through based on calculations from the band structure of Ref. 18. We do not want to go here into such details, because we want to compare the effective masses in ScN with those of the other rare earth nitrides, where there exists no such detailed band structure calculations because of the 4f states. So we take a simplified analysis using the measured optical carrier concentration [20] neff = 9.3 × 1019 and the formula wpo2 = 4pe2neff/moeff with moeff the optical mass of an electron hole pair and find moeff = 0.13 me, in good agreement with Ref. 18 where it was also 0.13 me. Of course we have to take into consideration that this is a mass averaged over all bands.
The last analysis for ScN concerns the phonon modes. In Figure 4, we show the decomposition of the imaginary part of the dielectric function in the far infrared into a phonon, Drude and inter-band contribution. wTO at G is observed at 45 meV and no different interpretation is possible. In Figure 5, we show the real part of the dielectric function in the far infrared and with the same decomposition as before we obtain the static and optic dielectric constants. The static DK can be directly taken from the figure and it amounts to estat = 60 and eopt to 5.2 (second zero crossing of e1 (outside Figure 5). Using the Lyddane-Sachs-Teller relation estat/eopt = (wLO/wTO)2, we can calculate wLO = 155 meV. Of course, the coupling of wLO with a longitudinal plasmon results in a plasmaron. We mentioned already that the calculation of the dielectric constant eopt in Ref. 19 is not correct due to the limited spectral range, but we can ask ourselves what it means to use a Lyddane-Sachs-Teller relation derived for an insulator in a semimetal in which the charge carriers have been theoretically eliminated? The separately measured Raman effect [20] on the ScN crystal yields optical modes near 84 meV and acoustic modes near 45 to 52 meV. And in this measurement the electrons are present. But in these rock-salt crystals the Raman effect is symmetry forbidden, but a second order effect is induced by defects. But now, the Raman effect measures a phonon density of states with maxima at the L point. In Ref. 18, the TO and LO energies are calculated to be 67 meV and 79 meV, at variance with the experimental findings.
So we have been able to measure all experimentally accessible parameters of the ground and excited state of ScN single crystals and compare it with modern band structure calculations. The general agreement is excellent and theory and experiment define this material as an indirect semimetal with weak indirect band overlap of about 80 meV between p at G and d at X. The importance of the present analysis lies in the fact that the band structure of most rare earth nitrides will be the same as for ScN, of course the 4f levels have to be introduced which will change the overlap of the p and d bands and thus the carrier concentration/rare earth ion. And, of course, magnetism will enter the picture.
5. GdN
One of the most interesting rare earth nitrides is GdN. Dozens of different publications have been presented over the years, disagreeing in most respects. The stoichiometry and the type of magnetic order are the main problems. In principle elastic neutron scattering in zero external field should solve the problem, but Gd has one of the largest neutron absorption cross sections and no neutron scattering is possible [6] . Busch et al. [23] [24] claimed polycrystalline and non-stoichiometric GdN as ferromagnetic, Junod et al. [25] , McGuire et al. [26] , Gambino et al. [27] , Li et al. [28] ,Vogt and Mattenberger [4] and Hirayama et al. [4] just as well, while Wachter [22] , Wachter and Kaldis [29] [30] showed that stoichiometric single crystals of GdN are antiferromagnetic for practically zero magnetic field, but become ferromagnetic with enhanced magnetic field [31] . Here the paper by Leuenberger et al. [32] on GdN films deserves special attention. They have a lattice constant of 1.5% larger than the one of Li et al. [28] , which is 4.981 Å, thus 5.055 Å. Nobody had such a large lattice constant, but their preparation method makes it likely that they have surplus nitrogen in interstitials and the films are by their own statement off-stoichiometry. As a consequence they have ferromagnetic GdN, but semiconducting material. Also with the electronic structure there is international disagreement, inasmuch as Wachter and Kaldis [29] could show on stoichiometric single crystals that the material is a semimetal, whereas band structure calculation by Hasegawa and Yanase [33] and the band structure calculation by Petit et al. [16] claim GdN to be a semiconductor.
It is quite clear that the problems arise with the introduction of the 4f7 state into the compound as compared with ScN. Since the DFT [16] cannot display the localized multi-electron 4f7 state in the otherwise one electron ground state theory Wachter has already 1978 [34] derived a tight binding scheme for EuS and GdN which shows the 4f7 state together with the p and d bands in a relative energy arrangement. It is found that in divalent EuS the localized 4f7 state is about 1.7 eV below the Fermi level EF and above the p bands of sulfur and in trivalent GdN the 4f7 is about 9 eV below EF and below the p band of nitrogen. Exactly this value is shown when measuring XPS photoemission. X-ray photoemission is especially sensitive and intensive to 4f (or 5f) states and in Figure 6 we display such a measurement [35] . As we showed above [15] [31] the width of the 4f7 ground state is less than 10−4 eV, but when an electron is removed from the 4f7 state by photoemission, the remaining 4f6 state can be in various excited states of the 7FJmultiplet, which has a width of about 0.6 eV (plus experimental resolution) [35] . In Figure 6 we show an XPS spectrum of GdSb [35] which agrees roughly with the more recent XPS spectrum on GdN of Ref. 32, which, with respect to the 4f state, has the same arrangement, the 4f7 sate is 8 - 9 eV below EF. This is quite important, because Kasuya et al. [36] stress the importance of p-f mixing for the explanation of the magnetic behavior―but in GdN there is no p-f mixing because the 4f7 state is much lower than the p band (see Figure 1), which stretches only to about 4.75 eV below EF. From the theoretical point of view, this is quite clear since the 4f7 state with its 8S7/2 configuration and its half filled 4f shell is the most stable state and thus the lowest in energy of all rare earth pnictides.
This, of course, has another consequence: There exists a so called “spectral repulsion term” between f states of the cation and p states of the anion. So the low energy 4f7 states push up the p states of nitrogen, enhancing thus the indirect p-d overlap compared with ScN, resulting in a larger carrier concentration in GdN compared with ScN. And, of course, there is a p-d hybridization, which in classical words is a certain covalency.
We used single crystals of GdN prepared and grown with methods described above, having an edge length of about 3 mm. These crystals have been chemically analyzed by the micro Kjeldahl method [11] and are found to be exactly stoichiometric (±0.5%). The lattice constant in the rock-salt structure was 4.984 Å. The following measurements have all been made on the same single crystal. The electrical resistivity at 300 K was 4 × 10−4 Wcm with a positive temperature gradient, i.e. metallic (see Figure 7) or the electrical conductivity was 2.5 × 103 (Wcm)−1. The negative Hall coefficient was n = 1.9 × 1021 cm−3, i.e. a factor 3.2 larger than for ScN. This results in n/Gd of 0.06. The mobility from s = enm yields m = 8 cm2/Vsec. This is dramatically less than the m = 260 cm2/Vsec in ScN and is due to the scattering of charge carriers on spin fluctuations in GdN.
Figure 6. XPS measurement of GdSb, exhibiting the final state 7FJ of the photoemission process (35).
Figure 7. Electrical resistivity of GdN with and without a magnetic field of 1 T (31).
The quantity n/Gd = 0.06 is the essential number in the whole field. As we have described already above, any excess of Gd in GdN above the stoichiometric ratio will introduce additional carriers and crystals with GdN0.98 yielding n/Gd = 0.08 have a completely different physical behavior. They are clear cut ferromagnets even for H®0. As elucidated further down, part of the magnetic exchange is a RKKY interaction, which depends on the carrier concentration. For small carrier concentrations, one is in the ferromagnetic lobe, so only the minimal carrier concentration can exhibit antiferromagnetism.
The point is: everyone can produce ferromagnetic GdN with non-stoichiometric samples or high magnetic fields. The art is to reduce the carrier concentration to the lowest possible value with perfect stoichiometry to find antiferromagnetism for H ®0 [22] [29] [30] . One can turn the statement around: whoever has ferromagnetic GdN for H®0 has a non-stoichiometric sample.
Measurements without magnetic fields are of great value because the application of a magnetic field will transform the antiferromagnetic GdN into a ferromagnet. We show in Figure 7 the temperature dependence of the electrical resistivity of GdN and generally find metallic (semimetallic) behavior with a nearly linear decrease of the resistivity (phonons) until about 80 K. Then we observe a kink at about TN = 40 K caused by the onset of antiferromagnetic order. This curve is very similar to the one of GdP [34] [37] where there is no doubt about the type of magnetic order and which has a TN of about 16 K. When we apply a magnetic field of 1 T to our GdN crystal (Figure 7) the resistivity starts to increase below about 70 K due to the onset of ferromagnetism and for low temperatures a sort of saturation is observed. The different behavior without and with magnetic field is a clear indication that we change the type of magnetic order in GdN, from antiferromagnetism at TN = 40 K to ferromagnetism with a Tc near 70 K.
Since with a magnetic field of more than 3 kOe GdN becomes ferromagnetic below about 70 K we expect an exchange splitting of the nearly empty 5d band into spin polarized sub-bands. The carrier concentration in these sub-bands is now about a factor two less, even when the indirect p-d overlap gets somewhat enhanced. As a consequence the resistivity in the ferromagnetic state is higher than in the antiferromagnetic state and exhibits something like a ferromagnetic saturation at low temperatures.
Another field free measurement on GdN is the specific heat [38] [39] , already from 1966 and 1969, which agree amongst each other on ferromagnetic polycrystalline samples, showing a Tc of 67.4 K. A more recent (1994) measurement by Li et al. [28] on claimed stoichiometric (but only phase pure) ferromagnetic GdN yields a Tc of 58 K, but states “there is (so far) no information about the magnetic transition of GdN from specific heat measurements” [sic], On the other hand their specific heat shows two transitions, one at 20 K and one at 58 K. They have obviously an inhomogeneous pressed powder sample with a nearly stoichiometric part and a non- stoichiometric part, but they write the sample “is not very pure”.
Another field free measurement is the optical reflectivity of GdN single crystals [40] . The reflectivity is shown in Figure 8 between 30 meV and 13 eV and a KK analysis yields e.g. the real part of the optical conductivity s1, i.e. the absorptive part (Figure 9) [40] . We have a relation of s1(w) = we2(w)/4p.
The dominant feature is again the minimum due to the plasma resonance of the free carriers. It is obvious again that the material is metallic (semimetal). Regarding inter-band transitions we have now p-d transitions just like in ScN but also f-d transitions from the 4f7 state to empty states above EF. There are at least double as many optical transitions than in ScN, so we will refrain from an assignment. Since f-d transitions have a much higher oscillator strength than p-d transitions, the maximum in the optical conductivity must correspond to this transition. This is between 9 and 10 eV and it corresponds exactly to the XPS photoemission measurement of Figure 6 where we find the 4f7 state about 9 eV below EF. The plasma resonance wpo2 = 4pe2neff/moeff with moeff the optical effective mass of the carriers at EF and noeff the optical carrier concentration. noeff taken from the Hall effect is n = 1.9 × 1021 cm−3 and we can compute the optical effective mass moeff = 0.8 me. This is appreciably larger than the moeff = 0.13 me of ScN and is due to a certain virtual f admixture to the 5d band at X.
We will describe now a new effect on GdN, namely a temperature shift of the plasma edge. Measured with a different single crystal than above and with a different optical apparatus, we show in Figure 10 the reflectivity near the plasma minimum in function of temperature. We observe a blue shift with decreasing temperature. When we cut the curves at 30% reflectivity, we can observe the shift of the plasma edge with temperature, which is displayed in Figure 11. We look at first at the field free curve and see that the blue shift with decreasing temperature saturates at low temperatures. No anomaly with any type of magnetic order is observed. Since the plasma frequency wpo depends only on the carrier concentration noeff or n (see above), it must be this quantity which changes. In first approximation, we assume that the number of free carriers remains constant, but the vo-
Figure 8. Reflectivity of GdN between 30 meV and 13 eV.
Figure 9. Real part σ1 (absorptive) of the optical conductivity of GdN.
Figure 10. Reflectivity of GdN near the plasma edge for temperatures of 10 K, 100 K and 300 K.
Figure 11. Shift of the reflectivity at 30% of GdN in function of temperature with and without a magnetic field of 1.2 T.
lume of the crystal is reducing with temperature, (temperature contraction), which means that the carrier concentration enhances with a blue shift of the reflectivity. If this is the case we expect a saturation at low temperatures, as observed. When we apply a magnetic field of 1.2 T, we observe a “red shift” of the curve below about 70 K and this has certainly to do with the now ferromagnetic sample.
This is very much reminiscent of the discovery of the “red shift” of the absorption edge of ferromagnetic semiconductors 1964 [13] [14] [41] , which is due to an exchange splitting of the 5d conduction band upon ferromagnetism. Below 70 K, it can now only be the carrier concentration, which becomes reduced. But just as for the ferromagnetic semiconductors [13] [14] [41] also in ferromagnetic GdN with a nearly empty 5d conduction band, the band will exhibit an exchange splitting. In a first idea one may think that the indirect overlap of p and d band gets enhanced, but we have to consider that the exchange split 5d band now consists of spin polarized sub-bands where each state in the band can now only be occupied by one electron instead of the two in the spin degenerate d band. Since this is a reduction of the carrier concentration by a factor two, the small enhancement of the few percents carriers due to an enhanced p-d overlap is negligible. This experiment is then in complete agreement with the above described resistivity measurement with and without magnetic field in Figure 7: in a magnetic field the resistivity increases below about 70 K due to the exchange splitting of the 5d band.
It is quite satisfying, that in the scientific life of the author a second time a “red shift” due to an exchange splitting of a ferromagnetic material has been discovered. But it is also evident that in the field free case no such exchange splitting is observed, so the questioned magnetic order at about 40 K must be antiferromagnetism [22] [29] [30] .
We are now coming to direct magnetic measurements on GdN, such as have been reported everywhere [2] - [5] , [8] [9] [22] - [32] [37] , (only a selection of authors). As we mentioned several times, the stoichiometry is the essential parameter. This can be seen in Figure 12 where already 1972 [22] the magnetism of GdN has been investigated with several preparation modes. The hydride and amalgam preparation (described in the introduction) yields polycrystalline, generally non-stoichiometric samples. In fields of 13 kOe they look ferromagnetic with saturation moments of 7 mB. But the magnetism is defined for H®0 and we observe a clear-cut ferromagnetic behavior in the initial susceptibility at 10 Oe with a Tc near 70 K. In contrast, the re-re-ground and re-re nitrified sublimed small single crystals (1/10 mm), found to be stoichiometric by the micro Kjeldahl method (see above) show for reduced magnetic fields a maximum in the magnetization and in the initial susceptibility of 10 Oe a sharp kink at 20 K as typical for an antiferromagnet with zero magnetization for zero temperature and near zero field. We realize that within the precision of the Kjeldahl method (±0.5%) we find for stoichiometric material always antiferromagnetism for GdN, but still a variation of the Néel temperature between 20 and 40 K [22] [29] [31] . Here we have to criticize again the paper by Li et al. [28] , who erroneously claimed that the specific heat has not been measured before them and who have an inhomogeneous sample with 2 transition temperatures of 20 and 58 K. The former agrees perfectly with the one reported by us [22] and the second is at variance with former measurements of the specific heat of 67.4 K [38] [39] , which however, are in agreement with our ferromagnetic transition temperature of about 70 K (see Figure 12). We are left with the problem that within the precision of the Kjeldahl method of ±0.5% stoichiometric small single crystals are antiferromagnetic with a TN of 20 K [22] and stoichiometric large single crystals are antiferromagnets with a TN of 40 K [29] [31] . That means, minute changes in stoichiometry can change the transition temperatures and also the type of magnetic order. In any case the paramagnetic Curie temperature qp is 79.14 K when measured in a field of 13 kOe.
In Figure 13(a) we show a very modern measurement of the real susceptibility [42] (not initial susceptibility) of GdN stoichiometric single crystals in a very sensitive SQUID cryostat in an applied field of only 10 Oe. The signature is again strictly antiferromagnetism with a TN of 33.3 K. In Figure 13(b), the reciprocal susceptibility is shown. (The single crystals had to be cleaved to a minute size, because the SQUID was so sensitive. As a consequence the crystals could not be aligned with their crystal axis [100] parallel with the magnetic field).
In Figure 14, we show the magnetization of GdN and GdN1-xOx, this because oxygen is the most probable contaminator in handling GdN in air. GdN exhibits for small fields a reduced slope than would correspond to a ferromagnetic GdN. Again this is typical for an antiferromagnet, which becomes ferromagnetic in fields of more than about 3 kOe. The correct description of stoichiometric GdN is thus metamagnetism [29] [31] .
We are coming now to the theoretical exchange interactions in GdN. Gd with its ground state configuration 8S7/2 of the 4f7 electrons is especially simple because the S state without orbital momentum has no crystal field levels and the rock-salt structure is also crystallographically extreme simple. Since we have shown that the magnetic structure for stoichiometric GdN is antiferromagnetism for H®0, the paramagnetic Curie temperature θp should be negative or near zero. But the Curie-Weiss law has only been measured in large magnetic fields around 10 kOe, where the material is ferromagnetic, thus θp = 79, 14 K. Thus in Figure 13(b), we show 1/c in only 10 Oe applied field, but the paramagnetic Curie temperature is still not negative, but about 40 K, very different from the standard 79 K as claimed up till today [42] . Because of this problem we cannot use the standard
Figure 12. Magnetization and initial susceptibility of GdN, prepared with various methods and measured in different magnetic fields between 13 kOe and 10 Oe. (22).

Figure 13. (a) The susceptibility of small GdN single crystals measured in a SQUID in a magnetic field of only 10 Oe (31); (b) The inverse magnetic susceptibility of small GdN single crystals in a field of 10 Oe (31).
Figure 14. The magnetic moment of stoichiometric GdN and various GdNxO1-x single crystals (29).
molecular field equations kBθp = (2/3)S(S+1)(12J1 + 6J2) = 126 J1 + 63J2 and TN = 2/3S(S+1)(−6J2) = −63 J2. In addition, we have a RKKY contribution due to the free carriers in the conduction band kBDTc = (n/Gd) (2
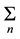 Jn(êr-Rnê) ás・Snñ with s the spin of the electron and Sn the ion spin.
Jn(êr-Rnê) ás・Snñ with s the spin of the electron and Sn the ion spin.
Goodenough [43] proposed for an insulating magnetic material for the ferromagnetic exchange J1 a cation- cation super-exchange with virtual transfer of a 4f electron to the 5dt2g excited state of a neighbor cation. The coupling gives in third order perturbation of the energy J1 = t2Jfd/2S2U2(f-dt2g), U(f-dt2g) being the energy difference 4f7-5dt2g band and Jfd is the intra-atomic exchange constant, which has been estimated from atomic data to be about 0.1 eV [36] . t is the transfer integral, estimated to be about 0.15 eV [36] . If we use for U (f-dt2g) the measured value from the optical absorption (Figure 9) or the XPS value from Figure 6 (f-centre 5dt2g) of 10 eV, then we obtain for the ferromagnetic contribution J1 = 0.07 K, an unusual small value, which is due to the large U(f-dt2g). For the antiferromagnetic exchange J2 Kasuya and Yanase [36] propose an indirect super-exchange involving the antibonding deg orbitals of the cation and the p orbitals of the anion. They propose J2 = −(1/2)b4Jfd2/U(p-deg). U(p-deg) is the energy difference between the p band and the 5deg band, taken from Figure 1 to be about 0.4 Ry or 5.4 eV. b2 is a covalency factor representing the hybridization between p and 5deg band, taken as bp6 + 5deg・b2 has been estimated to be between about 0.1 and 0.2 [36] , we take b2 as 0.15 and can compute J2 = −0.35 K. With this value we can calculate TN = −63 J2 = 22 K, not bad for the experimental values between 20 and 40 K (see Figure 12, Figure 13(b)), but this still corresponds to an insulating material. But theoretically this is a clear cut antiferromagnet with such a large J2 and such a small J1. If GdN is thought to be a ferromagnet, then this can only be caused by the RKKY interaction, which for low carrier concentration is ferromagnetic.
To exploit the effect of the carrier concentration on the magnetism due to the RKKY interaction we should measure mixtures between GdN (6% carriers) and GdO (100% carriers), but GdO does not exist. Instead we have measured in the system GdP-GdS (both unquestioned antiferromagnets) the effect of carrier concentration on θp (because in GdP even a magnetic field of 1 T cannot make the material a ferromagnet) [34] [44] . This is shown in Figure 15 and it is clearly seen, that up to about n/Gd of 20% the RKKY interaction is positive, i.e. ferromagnetic. The maximal contribution is at about 15%. Thus it is evident, that only the lowest carrier concentration can make GdN antiferromagnetic. With our n/Gd = 0.0 6 we probably have gotten the intrinsic value of carriers due to the p-d indirect band overlap (see Figure 1). Since GdN has the smallest lattice constant of all Gd pnictides, the term n/Gd Jn(çr − Rnç) is largest, e.g. for equal carrier concentration in GdP and GdN a certain radius r of an electron orbit includes in GdN more ion spins Sn than in GdP. Therefore GdN is more sensitive to the ferromagnetic contribution of the RKKY interaction than in GdP. In fact with n/Gd = 0.08 GdN is already ferromagnetic. On the other hand extrapolating the carrier concentration in Figure 16 to zero (dashed line) we obtain for the now insulating material a clear negative θp, showing that the super-exchange mechanisms alone are antiferromagnetically.
Jn(çr − Rnç) is largest, e.g. for equal carrier concentration in GdP and GdN a certain radius r of an electron orbit includes in GdN more ion spins Sn than in GdP. Therefore GdN is more sensitive to the ferromagnetic contribution of the RKKY interaction than in GdP. In fact with n/Gd = 0.08 GdN is already ferromagnetic. On the other hand extrapolating the carrier concentration in Figure 16 to zero (dashed line) we obtain for the now insulating material a clear negative θp, showing that the super-exchange mechanisms alone are antiferromagnetically.
Figure 15. Paramagnetic Curie temperature versus free electron concentration of GdP, GdP/GdS and GdS (44).
Figure 16. Resistivity of TbN without and with a magnetic field of 2 T. The inset shows the initial susceptibility in a field of 10 Oe (45).
Since for all other rare earth nitrides, the energy difference U (f-dt2g) is less than in GdN one may speculate that some compounds may be ferromagnetic already due to the exchange contributions. But this is not the case, since in all other rare earth nitrides the ground state is crystal field split.
Thus in conclusion of the GdN chapter we can state that stoichiometric GdN for temperatures near zero and magnetic fields towards zero (10 Oe) is an antiferromagnet, but becomes ferromagnetic above magnetic fields of about 3 kOe. The correct term is metamagnetism. The electrical behavior is metallic (semimetallic).
A recent article on GdN single crystals collects all the above arguments [31] .
6. TbN
Same problem, same solution! Namely, stoichiometric large single crystals. TbN is reported as ferromagnetic by Child et al. [6] with a Tc of 42 K. Stutius [39] reports it also as ferromagnetic with a Tc of 33.7 from specific heat measurements (but this kind of measurement cannot distinguish between ferro- and antiferromagnetism). Vogt and Mattenberger [4] use both values, but stay with ferromagnetism, and Vogt and Mattenberger [3] claim TbN “mostly” ferromagnetic and report some peculiarities in the neutron scattering [6] . Lately Hirayama et al. [5] claim TbN also as a ferromagnet. With the exception of Child et al. [6] , who report about nitrides with 95% nitrogen, nobody has checked the stoichiometry of their material, an X-ray purity is not enough to state stoichiometry, but see above.
To make the final conclusion already here: TbN is an antiferromagnet with a TN of 31 K when produced stoichiometrically and been checked with the micro Kjeldahl method [11] .
We used single crystals of TbN [45] prepared and grown with methods described above, having an edge length of about 3 mm. These crystals have been chemically analyzed by the micro Kjeldahl method [11] and are found to be exactly stoichiometric (±0.5%). The lattice constant in the rock-salt structure was 4.933 Å. The following measurements have all been made on the same single crystal. The electrical resistivity at 300 K was 1.1 × 10−4 Wcm with a positive temperature gradient, i.e. metallic (see Figure 16) or the electrical conductivity was 9.1 × 103 (Wcm)−1. The negative Hall coefficient was n = 9.9 × 1020 cm−3, i.e. a factor 1.7 larger than for ScN. This results in n/Tb of 0.03. The mobility from s = enm yields m = 57 cm2/Vsec. This is again less than the m = 260 cm2/Vsec in ScN and is due to the scattering of charge carriers on spin fluctuations in TbN.
In Figure 16, the resistivity is measured down to 4.2 K in zero external field or with 2 T. The field free curve exhibits a sharp peak at 31 K, which is strongly reduced in an applied magnetic field. This implies that an induced ferromagnetic order develops [45] . In this sense TbN is like GdN. The inset of Figure 16 shows the initial susceptibility with 10 Oe and it points clearly to antiferromagnetic behavior with TN = 31 K. The measurement of the specific heat of TbN is with 33 K not so far away [39] , but what shall we do with a Tc of 42 K [6] from neutron scattering? All non-stoichiometry? Nevertheless, Junod et al. [25] could reach on non-stoichiometric powder of TbN in a large magnetic field the saturation magnetization of 9.3 mB, whereas the theoretical value of gJ is 9 mB.
In Figure 17(a), we show the optical reflectivity between 3 meV and 10 eV on cleaved single crystals. On first sight the plasma edge is overwhelming and confirms the metallic behavior, which was stated already before. The plasma energy wpo = 0.9 eV. The plasma edge exhibits a blue shift upon cooling to 10 K of the same size as observed in GdN (Figure 10). We use the same explanation: the plasma edge depends only on the effective optical carrier concentration neff. We assume, as with GdN, that the number of carriers stays constant upon cooling, but a constriction occurs, so that the carrier concentration and thus wpo increases, causing a blue shift of the plasma edge. As with GdN nothing occurs at the onset of magnetic order at 31 K, so it is again evidence for an antiferromagnet. A magnetic field has not been applied. From an analysis of the plasma edge wpo2 = 4pe2neff/moeff (with neff = n), we obtain the optical effective mass moeff = 1.7 me.
For the electronic structure of TbN we take at first a look at Figure 18, which displays a sketch of a density of states diagram (after [46] ). We observe that the half filled 4f7 state is with about 7 eV not so far down as with 9 eV in GdSb (Figure 6). As we argued before in Gd compounds the 4f7 is the most stable 4f configuration. But Tb3+ has 8 4f electrons, so the 8th electron enters the 4f shell with spin down and about 4 eV above the 4f7 state or about 3 eV below EF. Thus the highest 4f state mixes much stronger into the p band and into the conduction band, which is the cause of the enhanced effective mass of 1.7 me, compared with 0.9 me in GdN.
A KK analysis reveals peaks in the absorptive part of the optical conductivity in Figure 17(b) at 3 and 7 eV and represents interband transitions from 4f7 and 4f8 to EF and corresponds exactly with Figure 18. These 2 transition energies match exactly those obtained with XPS on Tb metal [35] .

Figure 17. (a) Reflectivity of TbN between 1 meV and 10 eV. The inset shows details near the plasma edge (45); (b) The optical conductivity of TbN between 1 meV and 10 eV. The inset shows the real part of the dielectric constant near the plasma edge (45).
Figure 18. Electronic structure of TbN and HoN [46] .
Thus in conclusion of the TbN chapter, we can state that stoichiometric TbN for temperatures near zero and magnetic fields towards zero (10 Oe) is an antiferromagnet, but becomes ferromagnetic above magnetic fields of about 3 kOe. The correct term is metamagnetism. The electrical behavior is metallic (semimetallic).
7. HoN
With stoichiometric single crystals of HoN we want to demonstrate another aspect of the rare earth nitrides, namely the magnetization in the various relevant crystallographic directions. HoN (and HoP) were standard materials for neutron scattering in early times [6] and different spin orientations in 7 consecutive crystal planes have been discussed. Nevertheless, HoN was stated as ferrimagnetic [3] [4] [6] although we consider that typology as not fortunate. Generally, a ferrimagnet has at least 2 different magnetic moments on different ions, like Fe3+ and Fe2+ in Fe3O4 (magnetite) or in other ferrites. In HoN, there is only one magnetic ion, but the different spin directions in the 7 planes neither compensate as in an antiferromagnet nor do they add up to the full magnetic moment of gJ.
We have discussed already the three exchange mechanisms for GdN (see above), which hold for all rare earth pnictides: the next neighbor ferromagnetic super-exchange J1 and the next nearest neighbor antiferromagnetic super-exchange J2. For all rare earth nitrides, these 2 exchange mechanism result in antiferromagnetism. Only the third RKKY interaction can, depending on the carrier concentration, yield additional ferromagnetic exchange for low carrier concentration (Figure 15) or antiferromagnetic exchange for large carrier concentration. As discussed before only stoichiometric compounds have the minimum-the intrinsic-carrier concentration due to p-d indirect band overlap. Generally, one is in the ferromagnetic lobe of the RKKY interaction with carrier concentrations in the percent range.
We show in Figure 18 the schematic electronic structure of HoN with 7 spins up and 3 spins down, yielding a ground state of 5I8. The lattice constant in the rock-salt structure is 4.873Å [10] In Figure 19 we show the optical reflectivity of HoN single crystals [40] between 0.030 and 12 eV. The sharp plasma edge of the charge carriers is clearly visible indicating again the metallic nature of HoN. A KK analysis could be made and the absorptive part of the optical conductivity is shown in Figure 20. At about 3 and 8 - 10 eV, we observe the 4f-EF transitions, which agree with XPS data of Ref. 35 on Ho metal. An analysis of the plasma edge yields wpo = 1.5 eV and 5% charge carriers/Ho ion. The effective mass can be calculated from wpo and n = 1.6 × 1021 cm−3 to be moeff » 1 me.
Child et al. [6] find for HoN ferrimagnetism with Tc = 18 K, The specific heat reveals 13 K [39] , the same has Vogt and Mattenberger [4] , who also report a θp of 12 K. We show in Figure 21 the reciprocal susceptibility of HoN stoichiometric single crystals.
g [J(J + 1)]1/2 = 10.6 and gJ = 10, so the slope of the reciprocal susceptibility is 10.25 mB and agrees reasonably well with theory. But the paramagnetic Curie temperature θp is with 6.7 K much less than the formerly reported value of 12 K [4] (this is even with the same apparatus!). How can it be that standard type of measurements like magnetization, neutron scattering and specific heat which have differences up to a factor 2? It’s the stoichiometry, stupid!
In Figure 22, we show the magnetization of HoN of unknown stoichiometry up to fields of 40 T or 400 kOe. The different symbols represent data from different machines [47] . Everyone would agree that this sample is ferromagnetic, showing the theoretical saturation with gJ = 10 mB. However, we know already from the neutron scattering of Child et al. [6] that there is considerable anisotropy and the easy direction is á100ñ. Thus in the powder sample the individual grains orient along the magnetic field. If one uses single crystals this is not the case. This is a general problem of all magnetic measurements in large magnetic fields and on polycrystalline samples.
Figure 19. Reflectivity of HoN between 30 meV and 13 eV The inset shows the reflectivity near the plasma edge.
Figure 20. The optical conductivity of HoN between 30 meV and 13 eV.
Figure 21. The inverse magnetic susceptibility of HoN.
In Figure 23, we show the magnetization of stoichiometric single crystals in the relevant crystallographic directions. In no direction, we achieve the full magnetic saturation of 10 mB until 100 kOe or 10 T field. But we al-
Figure 22. The magnetization of HoN non-stoichiometric powder samples up to 35 T. The different symbols refer to different equipment (47).
Figure 23. The magnetization of stoichiometric HoN single crystals in the relevant crystal directions in fields up to 100 kOe.
so do not obtain the theoretical ratios of 1, 1/

8. YbN
We used single crystals of YbN prepared and grown with methods described above, having an edge length of about 3 mm. These crystals have been chemically analyzed by the micro Kjeldahl method [11] and are found to be exactly stoichiometric (±0.5%). The lattice constant in the rock-salt structure was 4.781 Å. The following mea- surements have all been made on the same single crystal. The electrical resistivity at 300 K was 8 × 10−5 Wcm with a positive temperature gradient [48] , i.e. metallic or the electrical conductivity was 1.2 × 104 (Wcm)−1. The negative Hall coefficient was n = 4.8 × 1020 cm−3, i.e. a factor 1.2 smaller than for ScN. This results in n/Yb of 0.013, the same as in ScN. The mobility from s = enm yields m = 156 cm2/Vsec. This is again less than the m = 260 cm2/Vsec in ScN and is due to the scattering of charge carriers on spin fluctuations in YbN.
In Figure 24, we show the optical reflectivity between 1 meV and 10 eV of a stoichiometric single crystal of YbN and a non-stoichiometric single crystal YbN0.96 even at 6 K [49] . There is not much difference with reducing the temperature, especially the shift of the plasma edge as observed in GdN and TbN is practically not visible since the plasma edge is so far in the infrared due to only a minute carrier concentration. But whereas YbN has only one significant peak in the infrared due to the TO phonons, the non-stoichiometric crystal has 2 peaks. In Figure 25, we show the imaginary (absorptive) part of the dielectric function as obtained from a KK analy-
Figure 24. Reflectivity of stoichiometric YbN at 300 K and of YbN0.96 crystals at 6 K (49).
Figure 25. The imaginary part of the dielectric function, ε2, of stoichiometric YbN at 300 K and YbN0.96 at 6 K between 1 meV and 10 eV. The inset shows the real part, ε1, of the dielectric function of YbN at 300 K near the plasma edge (49).
sis. The inset shows the real part of the dielectric function near its zero crossing. Again the off-stoichiometric crystal has 2 peaks, the stoichiometric one only one peak due to TO phonons. From an analysis of the plasma edge, we can obtain the effective mass moeff. Since there is no detailed band structure calculation of YbN as in ScN, we cannot make an effective mass analysis with heavy and light holes and electrons, thus we turn to an analogy, by comparing the plasma energies wpo of ScN and YbN. The uncoupled plasma resonance wpo in stoichio-
metric YbN is at 0.2 eV and 0.99 eV in ScN. wpo2 = 4pe2neff/moeff), so
for YbN an optical mass moeff » 2.73 me (there is a misprint in Ref. 49: 2.23 instead of 2.73). We discuss in a moment why the effective mass is so large compared with the other nitrides, but when it is so large this means that the bottom of the 5d conduction band is much flatter than usual. This has as consequence that the indirect overlap of the p band at G and the d band at X is much reduced, resulting in an extremely small carrier concentration of only 0.013/Yb ion (see above).
In Figure 26, we show an XPS and BIS (Bremsstrahlen Isochromat Spectroscopy BIS), on YbP [50] (because none is available on YbN, but with respect to the 4f states it is the same) where the latter measures the empty states above EF. We realize the final state spectra of the original 4f13 state below EF and the empty 4f14 state little above EF. Because of the hybridization of the 4f14 with the 5d band above EF there is a large 4f admixture to the 5d band, which causes a flat bottom of the 5d band and thus a reduced p-d indirect overlap. This on the one hand causes a large effective mass and on the other hand a low carrier concentration.
Since XPS and BIS have a low spectral resolution (about 1 eV) we refer to optical spectra in Figure 24 and Figure 25. For stoichiometric YbN, we find a peak at 0.2 eV, missing in non-stoichiometric YbN. This is indeed the transition from EF into the empty 4f14 state. On the other hand, the non-stoichiometric YbN has a plasma resonance wpo = 0.5 eV, much larger than the stoichiometric YbN with 0.2 eV. It has thus much more free carriers and the Fermi level is much higher in the 5d band, even filling somewhat the 4f14 state, especially at room temperature. We thus obtain a low level of intermediate valence with 4f13-4f145d mixing. We can now even observe an optical transition at low temperatures in the far infrared with 0.017 eV between the hybridization split 4f14 state. However, we want to stress that stoichiometric YbN is not intermediate valent, because the 4f14 state is not occupied [49] . There is, however the possibility that some Yb3+ ions in YbN are present as Yb2+ ions in YbN, and then this could be a reason that the carrier concentration is so low. Then the so far described empty 4f14 level in stoichiometric YbN could even be occupied to a low level with electrons even at low temperature and the material would be intermediate valent from the beginning. This, however, will not be the case as a special measurement [51] of the elastic constants will show.
We show then in Figure 27 an energy level diagram, where the hybridized 4f13 with the p valence band (p-f mixing) with its hybridization gap is seen and the 4f14- 5d hybridization with its hybridization gap for stoichiometric and non-stoichiometric YbN.
Figure 26. XPS and BIS of YbP (50).
Figure 27. Electronic structure of stoichiometric and non-stoichiometric YbN near the Fermi energy EF. To the left the bare electron 4f states are shown. In the middle part of the hybridized band structure is presented whereas in the right part a magnified sketch of the density of states near EF is shown (49).
We are coming now to the magnetic measurements and show in Figure 28 the inverse susceptibility of YbN in an applied field of 10 kOe. One obtains a θp = −93.5 K in contrast to ?11.6 K in Ref. 4 and authors quoted therein. A small dip is observed at about 3 - 4 K in the inverse susceptibility, resulting in a peak in the susceptibility and pointing to an antiferromagnetic order, even in an applied field of 10 kOe. This phenomenon is completely absent in the non-stoichiometric inverse susceptibility of YbN in Ref. 52. The initial susceptibility of stoichiometric YbN in 10 Oe has also a peak at about 5 K, but does not drop to zero at lower temperatures. The specific heat on non-stoichiometric YbN [39] has also a peak at about 3.8 K (but may be a Schottky anomaly) and neutron scattering confirmed antiferromagnetic order AF III [4] . The slope of the inverse susceptibility is with 4.44 mB only 2% different from the theoretical value 4.54 mB. The 2F7/2 ground state is split by the octahedral crystal field into a lower lying G6 doublet, a G8 quartet and a G7 doublet with an overall splitting of 890 K, in good agreement with specific heat data of Ref. 39. Thus there is complete agreement within the magnetic, specific heat and neutron scattering that stoichiometric YbN is a classical antiferromagnet. On an undefined polycrystalline sample of YbN a heavy fermion characteristic has been proposed [52] , but we have shown that this characteristic is typical for non-stoichiometric samples, where the large carrier concentration fills up partially the usually empty 4f14 state, whereas stoichiometric single crystals are definitely non heavy fermion. However, all other Yb pnictides, especially also non-stoichiometric YbN, with their large free carrier contribution, fill somewhat the 4f14 or one hole state (see Figure 27) and result in some intermediate valence [48] [49] or dense Kondo effect. This usually has also an effect in the electrical resistivity, but the one of stoichiometric YbN is a very smooth curve, in contrast to YbP and YbAs [48] . However, all Yb pnictides show antiferromagnetic order [3] [4] , although in YbP 0.41 K [48] is observed, in contrast to 0.7 K in Ref. 52.
Because of the controversy between the physical properties of different stoichiometric YbN samples we have performed a critical experiment being able to distinguish between both possibilities [51] . This is the surface acoustic wave SAW in a Brillouin scattering experiment. á100ñ cleaved single crystals of stoichiometric YbN have been excited with an Ar+ ion laser of 514.5 nm and sharp Stokes and anti-Stokes lines have been obtained. Because of the metallic character of the samples only surface excitations are predominant, but the excitation in the GHz range extends to about 3000 Å depth. The crystal is rotated within the á100ñ plane and the shift of the
lines is observed. For an isotropic cubic crystal the elastic moduli are C11 − C12 = 2C44 and vSAW =

the density of the crystal. VSAW for YbN is 3200 m/sec and the elastic moduli could be obtained: YbN, C11 = 385 GPa, C44 = 129 GP and C12 = 108 GPa. They also have been obtained for YbP and YbAs [51] . This permits the
calculation of the Poisson ratio n =

Figure 28. The inverse susceptibility of stoichiometric YbN single crystals. The full drawn curve is a fit with crystal field parameters. The inset shows the inverse susceptibility near its minimum (49).
son ratio (meaning also a negative C12) is a clear indication of intermediate valence or heavy fermion behavior [53] , which, however, is not the case.
On YbP there is a NMR measurement claiming heavy electron behavior [54] , but it is again the same problem of non stoichiometry as always. Excess electrons partially fill the empty 4f14 state little above EF as in Figure 26 and thus provoke the heavy fermion behavior. Stoichiometric YbP has a positive C12 and thus is non-heavy fermion [51] .
In a last effort we come to the phonon properties of YbN. The far infrared spectra and their KK analysis yield the TO phonons at G at 34 meV. As usual, the plasmon and the LO phonon couple to form a plasmaron, where the resonance is when e1 gets zero (Figure 25, inset). The decoupled wLO = 62 meV. Both phonon frequencies are appreciable softened compared with ScN: wTO = 45 meV and wLO = 155 meV. This is because of the larger mass in YbN than in ScN.
9. CeN
In continuation with this last chapter of interesting rare earth nitrides we will discuss CeN stoichiometric single crystals. Already by looking at the crystals one observes a difference to all other nitrides: CeN has an orange to golden color, in contrast to all other nitrides, which are black. It has been realized already 1963 [55] and 1969 [25] [56] by comparing the lattice constants of all rare earth nitrides, that CeN drops out of the regularity of the lanthanide contraction with a much smaller lattice constant than the neighboring PrN and LaN. In fact Kaldis et al. [57] investigated the phase relationship within the Ce-N system and found for stoichiometric CeN a lattice constant of 5,018 Å. Already 1969 [25] [55] it was realized that CeN was a mixture of tetravalent and trivalent CeN and Baer and Zürcher [58] interpolated between a hypothetical trivalent CeN and a tetravalent CeN a mixed valence of 3.46 at room temperature. But it was also clear by measuring the lattice constant up to 1000 K that the valence of CeN increased abruptly above 600 K with a concomitant increase of the trivalent Ce3+ [56] .
It is thus clear that CeN is a mixed valence compound or in its quantummechanical description an intermediate valence compound. But is it also a heavy fermion compound, which means that the Fermi energy lies in a high density of f-states at EF? It has already been stated [53] that every heavy fermion is also intermediate valent, but not every intermediate valent compound is a heavy fermion, example SmB6, where EF lies in a hybridization gap. The difference depends on the number of f electrons, odd or even. Ce3+ has one 4f electron and is odd, Sm2+B6 has 6 4f electrons and is even, but as well CeN as SmB6 are intermediate valent.
A beautiful experiment has been performed by Baer and Zürcher [58] , namely core level XPS on our CeN single crystals and on Ce metal. Because tetravalent Ce has no more f electrons one must resort to the influence of f occupation on the inner 4d electron shells (Figure 29). In the upper part is the spectrum of CeN and in the lower part the spectrum of metallic Ce at room temperature (b) or at 77 K (a), where it is known that Ce transforms to the a phase with a certain fraction of tetravalent Ce. Two new peaks appear, which are also present in CeN. It is thus clear that also CeN is intermediate valent. The XPS spectrum of the valence band [58] [59] (Figure 30) of CeN crystals and films shows a sharp peak at the Fermi level. This is the partially filled 4f band hybridized with the 5d band. This structure in reality is much narrower than shown in Figure 30 because of the low resolution of XPS measurements. In fact, a UPS measurement reveals this 4f-5d peak at EF much sharper [60] . In this narrow f band at EF we then expect a large density of states and electrons with heavy masses.
When the density of electrons at EF is so large as claimed we also expect a large temperature independent Pauli susceptibility. This is indeed the case and is shown in Figure 31, one of the most beautiful examples of
Figure 29. XPS spectrum of the Ce 4d level in CeN and metallic Ce: (a) at liquid nitrogen temperatures; (b) at room temperature (58).
Figure 30. XPS and BIS spectrum of CeN. The partially filled 4f and the empty 4f level can be discerned at EF (59).
Figure 31. Magnetic susceptibility of CeN in 5 Oe (31).
Pauli paramagnetism. Other strong Pauli susceptibilies are reported for the Pu chalcogenides [61] and some Am chalcogenides and pnictides [3] [4] . Now the susceptibility of unknown-stoichiometric CeN has been measured already 1963 [55] , and a temperature independent susceptibility has been found with c = 433 × 10−6 emu/mole. In 1969 [56] , no evidence of a temperature independent susceptibility has been observed but paramagnetism with a much smaller susceptibility than expected for a purely trivalent Ce3+. The authors have measured only down to 7 K whereas our measurements extend until 2 K. But they suggest that the strong increase of the susceptibility below about 100 K would be due to magnetic impurities, because a similar increase in the susceptibility has been observed for LaN and LuN, where no intrinsic magnetic ions are present. If so, our increase of the susceptibility commences only below about 20 K and suggests a much smaller content of a magnetic impurity. After all we used stoichiometric single crystals. Ce excess in CeN would lead to such a paramagnetic impurity [56] . When we plot 1/c in Figure 32 we see that the paramagnetic susceptibility below about 20 K extrapolates exactly towards 0 K, as would be expected for a magnetic rare earth impurity.
The value of our Pauli susceptibility of CeN extrapolated to T®0 is 700 × 10−6 emu/mole, appreciably more than in Ref. 55. The Pu chalcogenides PuS, PuSe and PuTe are other examples of Pauli susceptibility [3] [61] and PuTe e.g. has a Pauli susceptibility of about 300 × 10−6 emu/mole. The susceptibility and the g value of the specific heat are connected:


“heavy fermions” have g values up to 1600 mJ/mole K2 (CeAl3, CeCu6), there are others with g values of 24 (U6Fe) and 21(U6Co) [62] .
The density of states at the Fermi level contains the effective mass:
D(EF(0)) =


TF the Fermi temperature, taken to be 3000 K = 0.36 eV, corresponding to the width of the UPS peak at the Fermi level of Ref.60. The effective mass then turns out to be meff = 34 me.
The band structure is similar for most rare earth pnictides. It will be on the one hand like ScN [18] with an indirect overlap of the p band at G with the d band at X resulting in charge carriers with more or less normal effective masses. CeN has on the other hand also a fractionally filled f band at EF with heavy f electrons and a hybridization of f and d electrons. Here we have to come back to Figure 30, where not only the XPS results on occupied electronic states are shown, but in BIS (Bremsstrahlen Isochromat Spectroscopy) also the empty electronic states or bands [59] . The measurements are on CeN films of unknown stoichiometry and lattice constant [59] . The authors explicitly state that there is no overlap between the anion derived p band and the cationic d band. Thus the empty 4f band above EF is at most hybridized with the empty d band, but the occupied 4f state below EF is not hybridized with the d band. This is very confusing, because then it would not lead to f-d hybridization and intermediate valence. The proposed f occupation is with nf = 0.83 in disagreement with other results (nf = 0.35, see above).
Figure 32. The inverse magnetic susceptibility of CeN in 5 Oe (31).
The essence of the rare earth pnictides including ScN and most nitrides is that they have an indirect p-d overlap between the maximum of the p band at G and the minimum of the d band at X [18] [20] , with ScN the smallest overlap of only 80 meV. This overlap results in metallic conductivity and a certain amount of free carriers, measured in the Hall effect or the plasma resonance in an optical experiment. Now CeN with its small lattice constant, smaller than the neighbors LaN and PrN, has the largest p-d overlap of all nitrides, manifest in the largest plasma resonance of 3.8 eV of all nitrides (see below). So, there must be a large p-d overlap. In Figure 30 [59] , there seems to be no p-d overlap, but an XPS measurement is not very sensitive to p and d electrons, mostly sensitive to f electrons. If we do not shift the question to a lack of stoichiometry we are left with a problem.
In recent years, there are many band structure calculations on rare earth nitrides, in fact on CeN in Ref. [63] , on all nitrides in Ref. [64] , in Ref. [65] on CeN, in Ref. [66] on CeN (and another Ce compound) and in Ref. [67] on Ce pnictides and in Ref. [16] on all rare earth pnictides. However, band structure calculations of whatever type all suffer from the same drawback that in rare earths and their compounds localized 4f states still are narrow bands. E.g. in GdN the band structure is exactly as described above, with the indirect overlap of p (Γ) with d(X), with the 4f7 localized level 9 eV below EF [31] , but band structure calculations seem to find a small gap [64] , [16] between the maximum of the p band at G and the minimum of the d band at X, making the material a semiconductor. This is in contrast to experimental findings on stoichiometric GdN single crystals, which always were and are metals (semimetals [31] ). Also the claim that GdN is ferromagnetic is just as incorrect [31] , it is antiferromagnetic in very small fields. There exists no ferromagnetic rare earth pnictide in stoichiometric single crystals! In fact localized 4f levels have a width less than 10−4 eV, [31] , beyond the limits of band structure calculations.
However, in CeN there seems to be a way out. When 4f levels are found at the Fermi level as in Figure 30, then, by definition the 4f form narrow bands. As such they are taking part in the bonding of the crystal and the additional binding energy reduces the lattice constant. So the transition localized-delocalized is concomitant with a lattice reduction. This puts a question mark in the calculation of the degree of mixed valence in CeN derived from the lattice constant alone, comparing the radius of Ce3+ localized 4f with empty 4f in tetravalent Ce, offering a value of the valence of 3.45. Part of the reduced lattice constant is due to the bonding of 4f in CeN.
On the other hand, having a real 4f band at the Fermi level as in CeN makes band structure calculation much more credible and in fact all calculations agree even in detail with each other [16] , [63] - [67] . But in this compound the p-d band structure is different from the standard ScN like plus localized 4f. The maximum of the p band is shifted to X and the minimum of the d band remains at X, so there is a direct overlap p-d at X making the material a metal (not semimetal) (see Figure 33) [64] . This is in contrast to Figure 30 [59] where no p-d overlap is postulated. But it permits exactly a large free carrier concentration, which then is manifest in a high plasma resonance of 3.8 eV (see below). But we not only have a p-d overlap, evidenced in covalency, but also a f-d hybridization and a fractional occupation of the f band, permitting intermediate valence, as postulated since early times. But we also recall that BIS measures as final state the 4fn+1 state, for CeN the 4f2 level. The band structure calculation [64] shows the position of the empty 4f bands around 1 eV and the band with mixed d and f
Figure 33. Self consistent band structure of CeN. In red is the 4f partially filled 4f band and EF is at zero (64).
character crossing the Fermi level along Γ-X. The authors calculate 4f0.655d1.29, because there are also p-ele- ctrons in the d band. The general picture is agreeing mostly with the f states in Figure 30, but the p-d-and f mixing is in sharp contrast with Figure 30 [59] .
This f-d hybridization should also lead to a hybridization gap within the fractionally occupied 4f state as we have seen in YbN [49] but also in PuTe [53] , [61] , UPt3 [53] , [68] , CeCu6 [53] [69] [70] , U2PtC2 [53] [71] and CeAl3 [53] [72] . But the Fermi level will not be in the gap as in PuTe [53] , but in a density of states peak.
But the question remains: is CeN also a heavy fermion besides being intermediate valent? The above theoretically derived values of g and meff/me are not too exciting, but the Pauli susceptibility speaks for a large density of states at EF. Such a Pauli susceptibility has otherwise only been found in intermediate valent PuS, PuSe and PuTe [61] or Am chalcogenides and pnictides [3] [4] .
Stewart [62] in his review article of 1984 about heavy fermions describes 8 such materials, none has a Pauli susceptibility but all have a 1/c Curie-Weiss susceptibility with a negative qp. Of course, their g values and effective masses are often much larger than we described above. Even Ce compounds like CeCu6 and CeAl3 behave this way. But there is a lengthy discussion if one should consider the heavy fermions as due to the Kondo effect or a Kondo lattice. The conclusion is that it is “kondoesque” without commenting that a Kondo lattice with its f-d hybridization necessarily has a hybridization gap and the important point is the position of the Fermi level, in the gap or in the adjoining density of states peaks [53] . We show in Figure 34 the two densities of states peaks around EF for CeCu6 as derived from a far infrared optical reflectivity, permitting optical transitions between the two peaks [70] .
It is now clear that we have to measure the specific heat of our stoichiometric single crystals of CeN.
We used a 3He cryostat permitting temperatures down to 0.3 K and show in Figure 35 cp versus T below 2 K. In the magnetic field free case the specific heat is linear, extrapolating to cp = 0 for T = 0. There is a small peak at about 0.62 K, which has not the signature of a magnetic ordering. Magnetic fields up to 15 kOe do not enhance the peak or smear it out, but the linear part of the specific heat is enhanced due to the magnetic induced partial spin order and the corresponding magnetic energy.
All 8 heavy fermions discussed in the review article of Stewart [62] have such peaks at various low temperatures, besides peaks due to superconductivity or magnetic ordering. No explanation is offered in that article, but the essence of f-d hybridization is not understood: namely the two peak structure in the density of states near EF with a hybridization gap in between as exemplified in Figure 34 for CeCu6 [70] . This now is a classical two level system, which results in the specific heat in a Schottky anomaly at various temperatures, depending on the material and the degree of intermediate valence. Do not forget, that each heavy fermion is also intermediate valent, but not every intermediate valent material is a heavy fermion (example SmB6, PuTe, YbN) [53] .
A plot cp/T against T2 below 10 K shown in Figure 36 reveals a straight line with an extrapolated g (T®0) of
8 mJ/mole K2 and a slope b = 0.051 mJ/mole K4. With
diatomic molecule, we obtain Θ = 427 K. This should be compared with Θ = 320 K for LaN [39] and Θ = 355 K for PrN [39] . We observe that CeN does not fit in between, but has a Θ near 440 K like LuN [39] .
Figure 34. Reflectivity of CeCu6 at 5 K and 300 K. The inset shows the profile of the density of states near the Fermi level as inferred from experimental data (70).
Figure 35. Specific heat of CeN below 2 K with and without a magnetic field of 15 kOe.
Figure 36. C/T versus T2 of the specific heat of CeN.
In spite of the masses, which are in between those of LaN and PrN, CeN has a much smaller lattice constant due to the intermediate valence between Ce3+ and Ce4+. It would correspond to a Ce3+N under high pressure, which makes the lattice harder and thus the Debye temperature higher. It is remarkable that in Ref. 67, calculating also elastic properties of CeN, Θ is with 433 K practically the same as experimentally observed. However, the f-d hybridization should also lead to a negative c12, but it is calculated as positive. A negative c12 holds for all 4f-5d and 5f-6d intermediate valent materials [53] .
But it is a surprise that below about 2 K the g value shoots up like in a heavy fermion, but not reaching the high values as those. Nevertheless a temperature dependent g value is typical for heavy fermions. However, the values do not even reach the calculated values obtained from the Pauli susceptibility (see above) of 43 mJ/mole K2 but remain at about 15 mJ/mole K2. Thus CeN cannot be considered a heavy fermion, at most a “light weight” heavy fermion, but it is intermediate valent.
In Ref. 60 are high resolution UPS results on various Ce alloys reported, including CeN. Whereas we consider the experimental results as convincing when the sample quality is stoichiometric, the theory makes use of the single impurity Kondo or Anderson model of Gunnarson and Schönhammer [73] . However, this model is no longer adequate and one has to use the Kondo or Anderson lattice case. This model treats the hybridization more correctly and exhibits a two peak structure with a hybridization gap in between. This is experimentally shown e.g. in Figure 34 for CeCu6, where optical transitions are possible between the two peaks [53] [70] . In Figure 37, we show a density of states plot of the single impurity Kondo case (left) and the Kondo lattice case (right) [74] . But in Ref. 60 theory predicts the g value of the specific heat for T®0 to 170 mJ/molK2, whereas the experiment (see Figure 36 and Ref. 56) is 8 mJ/molK2, orders of magnitude off, and c (T®0) as 5.8 × 10−3 emu/mol, whereas the experiment (Figure 31) yields 0.70 × 10−3 emu/mol, off by nearly one order of magnitude. When the calculations are correct, then the starting point with the Gunnarson-Schönhammer single impurity model [73] is not adequate.
In an optical reflectivity measurement, we will observe at room temperature a plasma resonance in the near infrared due to p-d electrons with normal masses corresponding to some percents of charge carriers and at low temperatures an additional plasma resonance due to the heavy electrons in the far infrared. Such measurements have been performed by Marabelli et al. [68] on UPt3 and Marabelli and Wachter [69] [70] on CeCu6 and Awasthi et al. [72] on CeAl3 and are collected in Ref. 53. These far infrared reflectivity measurements at low temperatures are yet to be performed on CeN.
But between 30 meV and 12 eV the reflectivity could be measured on single crystals of CeN at 300 K [40] and it is displayed in Figure 38. The minimum due to the plasma resonance of free electrons and holes is visible at about 1.5 eV, superimposed by an interband transition at about 1 eV and a peak at about 2 eV, 4 eV and 8 eV.

Figure 37. Schematic spectrum of the density of states of (a) the impurity Kondo case and (b) the Kondo lattice, including split off bands at Ef and Ef + U and the many body resonance of width TK.. The scale TK is expanded for clarity (53, 74).
It is this peak at 2 eV which gives the crystals the orange to golden color.
A Kramers-Kronig (KK) analysis with suitable extrapolations to w®0 and w®¥ could be performed with this large spectral range [40] and the dielectric functions could be obtained. The optical conductivity s1 as the absorptive part is shown in Figure 39. In this representation only, even the small peak at about 1 eV, superimposed in the reflectivity with the plasma edge, is clearly discernible. These narrow peaks at 1 and 2 eV must be connected with the 4f level, in or out, because these narrow features are absolutely absent in other rare earth nitride spectra with low lying 4f’s.
In another representation of the imaginary part (absorptive) of the dielectric function e2 (s1(w) = we2 (w)/4p), one can decompose the contribution to e2 of bound




The result of the decomposition [76] of e2 into



Figure 38. Reflectivity of CeN between 30 meV and 13 eV. The inset shows the reflectivity near the coupled plasma resonance.
Figure 39. The optical conductivity of CeN between 30 meV and 13 eV.
Figure 40. Separation of the imaginary part of the dielectric function ε2 into interband transitions,


At 5 K the plasma resonance, Dwpo/wpo(300) = +5.3% and at 500 K ?10.5% and the carrier concentration Dnopt/nopt(300) = +10% at 5K and ?18% at 500 K. The measurement of the temperature dependence of the plasma resonance corresponds roughly to the Hall effect (with temperature independent moeff) and we learn that at 5 K we have more charge carriers than at 300 K and 500 K. This means that CeN is more tetravalent at low temperatures and more trivalent at high temperatures. Again this is concomitant with measurements of the temperature dependence of the lattice constant [56] , decreasing at low temperatures since the ionic radius of tetravalent Ce is smaller than of trivalent Ce.
The electrical resistivity of CeN at 300 K is 2 × 10−5 Ώcm, the smallest value of the described rare earth nitrides. Taking for the carrier concentration the above value of nopt = 0.33 el/ion and having with the lattice constant and fcc structure of 5.018 × 10−8 cm 3.16 × 1022 cm−3 ions we obtain 1.04 × 1022 cm−3 charges. From σ = enμ we estimate μ = 30 cm2/Vsec, an acceptable value. However, the thermoelectric power of Ref. 55 points to p type conductivity.
But we have to come back to the XPS and BIS measurements on CeN films of unknown stoichiometry and lattice constant [59] as shown in Figure 30. The authors explicitly state that there is no overlap between the anion derived p band and the cationic d band. Thus the empty 4f band above EF is at most hybridized with the empty d band, but the occupied 4f state below EF is not hybridized with the d band. This is very confusing, because then it would not lead to f-d hybridization and intermediate valence.
The essence of the rare earth pnictides is, including ScN and the nitrides, that except CeN, they all have an indirect p-d overlap between the maximum of the p band at G and the minimum of the d band at X [18] [20] [64] . This overlap results in the metallic conductivity and a certain amount of free carriers, measured in the Hall effect or the plasma resonance in an optical experiment. Now CeN with its small lattice constant, smaller than the neighbors LaN and PrN, has the largest p-d overlap of all nitrides, manifest in the largest plasma resonance of 3.8 eV of all nitrides. So there is a large p-d overlap at EF. As described above in CeN there is a direct overlap p-d at X, making the material a metal (not semimetal) [16] [63] -[67] . In Figure 30 [59] , there seems to be no p-d overlap, but an XPS measurement is not very sensitive to p and d electrons, mostly sensitive to f electrons. If we do not shift the question to a lack of stoichiometry, we are left with a problem.
But we can try to connect the optical transitions of Figure 39 with the combined XPS and BIS spectra of Figure 30. It is clear that the optical transition around 8 eV in Figure 39 goes from the maximum of the p band at G indirectly to the maximum of the d band in Figure 30. The 4 eV peak in Figure 39 would correspond to the direct p-d transition at G (consult Figure 30), the peak at 2 eV would correspond to a direct transition f-d at X and the peak at 1 eV in Figure 39 would be the famous transition occupied 4f to empty 4f across the hybridization gap. This transition has a low oscillator strength as an intra 4f transition, just as in CeCu6 in Figure 34 [70] . One should not forget that the red color in the television set is due to an intra 4f transition in Eu doped YVO3.
10. Conclusions
The problems of rare earth nitrides exemplified with ScN, GdN, TbN, HoN, YbN, CeN have been described and new measurements on stoichiometric single crystals are performed. Triggered by the claim of ferromagnetism for some nitrides, as collected in the review by Vogt and Mattenberger [4] the new results show, that none of the stoichiometric rare earth nitrides is ferromagnetic in low magnetic fields. The most interesting case is GdN, which for nearly 50 years and with hundreds of authors has been claimed to be ferromagnetic, and is now antiferromagnetic for low fields of about 10 Oe, becoming only ferromagnetic above fields of 3 kOe or with excess metal. The definition of spontaneous magnetic order is for applied fields towards zero. Since it has been shown with magnetic exchange interactions [31] that a significant contribution is the RKKY interaction, which depends on the carrier concentration and that only with the lowest possible carrier concentration achieved with perfect stoichiometry the correct magnetic order can be obtained.
In the example of HoN (and other powder materials), polycrystalline powder arranges the grains in an applied magnetic field with the easy direction in field direction, so magnetic saturation can be obtained. In single crystals, such a mechanical rotation of grains is not possible, so a magnetic saturation in fields of 10 T is not always achieved. So it is not only necessary to have stoichiometric material, but also single crystals must be grown and measured.
Since for many measurements (XPS, BIS, optical reflectivity) relatively large single crystals are necessary, a minimum size of about 2 mm edge length is necessary. The handling of the crystals in vacuum or inert atmosphere is essential and must be established.
In the review article of Vogt and Mattenberger [4] , NdN, GdN, TbN and DyN are reported as ferromagnetic, whereas HoN and ErN are reported as ferrimagnetic. All other rare earth pnictides are antiferromagnetic. In the present review article, it has been shown that GdN, TbN and YbN are antiferromagnetic. HoN is not ferrimagnetic but has a spontaneous magnetization, though not the saturation magnetization up to 10 T. NdN and DyN have been measured only on non-stoichiometric powder samples [25] and in high magnetic fields, where excess metal provokes excess electrons which throw the samples into ferromagnetism due to an enhanced ferromagnetic RKKY interaction. Thus, none of the rare earth nitrides is ferromagnetic. The correct term is metamagnetism.
For more than 50 years, research is going on with rare earth pnictides, especially nitrides. The handbook articles by Hulliger [2] and Vogt and Mattenberger [3] , authors and members of our institute collected most data available at the time of their printing. Kaldis et al. [57] described in detail the growth of stoichiometric single crystals and the handling of these crystals in inert atmospheres was a challenge by itself. For rare earth nitrides with their intrinsic low carrier concentration in the percentage range, off-stoichiometry in the percentage range can change the whole physical behavior and make antiferromagnets to ferromagnets and semiconductors to semimetals. Thus a theorist, not realizing the experimental problems, or believing the statements of the authors that their XRD tested samples are stoichiometric, may choose from antiferromagnets to ferromagnets and from semiconductors to metals and find agreement with his theory. So a critical review and comparison of the existing data together with new and significant experiments on well defined single crystals is essential so that theorists can test their theories. But theorists have their own problems, inasmuch as localized and itinerant electrons cannot be treated on the same level [16] and the calculation does not reach the sometimes meV overlap of p and d bands, deciding between semiconductor and semimetal. Only for ScN with no 4f’s and CeN with 4f bands, the theories have some credibility. In a recent paper [77] , some new results of CeN are collected.
Acknowledgements
The author is most grateful to Prof. Dr. Emmanuel Kaldis, who developed during his time at the Laboratorium für Festkörperphysik at ETH Zürich the growth of large and well defined stoichiometric single crystals of Rare Earth Nitrides. The SQUID measurements have been performed by Dr. N. Zhigadlo to whom the author is most obliged. The specific heat measurements on CeN have been carried through by J. Kanter and the electrical measurements have been performed by Dr. B. Frick during their PhD theseses. K. Mattenberger performed some magnetic measurements. For technical help by H.P. Staub and J. Müller, the author is most grateful.
Cite this paper
PeterWachter, (2015) Physical Properties of Some Stoichiometric Rare Earth Nitride Single Crystals. Advances in Materials Physics and Chemistry,05,96-131. doi: 10.4236/ampc.2015.53013
References
- 1. Matthias, B.T., Bozorth, R.M. and van Vleck, J.H. (1961) Ferromagnetic Interaction in EuO. Physical Review Letters, 7, 160-161.
http://dx.doi.org/10.1103/PhysRevLett.7.160 - 2. Hulliger, F. (1979) Rare Earth Pnictides. In: Gschneidner Jr., K.A. and Eyring, L., Eds., Handbook on the Physics and Chemistry of Rare Earths, Vol. 4, Ch. 33, North-Holland Publishing, Amsterdam, 153-236.
- 3. Vogt, O. and Mattenberger, K. (1993) Magnetic Measurements on Rare Earth and Actinide Monopnictides and Mono-chalcogenides. In: Gschneidner Jr., K.A., Eyring, L., Lander, G.H. and Choppin, G.R., Eds., Handbook on the Physics and Chemistry of Rare Earths, Physics-I, Vol. 17, Ch. 1, Lanthanides/Actinides, North-Holland Publishing, Amsterdam, 14-407.
- 4. Vogt, O. and Mattenberger, K. (1995) The Magnetism of Localized or Nearly Localized 4f and 5f Shells. Journal of Alloys and Compounds, 223, 226-236.
http://dx.doi.org/10.1016/0925-8388(94)09005-X - 5. Hirayama, Y., Nakagawa, T. and Yamamoto, T.A. (2011) Curie Temperatures and Modified de Gennes Factors of Rare Earth Nitrides. Solid State Communications, 151, 1602-1604.
http://dx.doi.org/10.1016/j.ssc.2011.07.021 - 6. Child, H.R., Wilkinson, M.K., Cable, J.W., Koehler, W.C. and Wollan, E.O. (1963) Neutron Diffraction Investigation of the Magnetic Properties of Compounds of Rare Earth Metals with Group V Anions. Physical Review, 131, 922-931.
http://dx.doi.org/10.1103/PhysRev.131.922 - 7. Sclar, N. (1964) Properties of Rare Earth Nitrides. Journal of Applied Physics, 35, 1534-1538.
http://dx.doi.org/10.1063/1.1713662 - 8. Busch, G., Junod, P., Vogt, O. and Hulliger, F. (1963) Ferro- and Metamagnetism of Rare Earth Compounds. Physics Letters, 6, 79-80.
- 9. Busch, G., Kaldis, E., Schaufelberger-Teker, E. and Wachter, P. (1970) Synthesis, Crystal Growth and Physical Properties of Rare Earth Nitride Phases. Colloques Internationaux du CNRS, 1, 359-373.
- 10. Kaldis, E. (1974) Principles of the Vapour Growth of Single Crystals. In: Goldman, C.H.L., Ed., Crystal Growth: Theory and Techniques, Vol. 1, Plenum Press, New York, 49-192.
- 11. Kaldis, E. and Zürcher, Ch. (1976) Solid State Chemistry and Physics of the Monopnictides and Monochalcogenides of some Trivalent Rare Earths. In: Lundin, C.E., Ed., Proceedings of the 12th Rare Earth Research Conference, Denver Research Inst., Denver, 915-934.
- 12. Cho, S.J. (1967) Spin Polarized Electronic Energy-Band Structure in EuS. Physical Review, 157, 632-640.
http://dx.doi.org/10.1103/PhysRev.157.632 - 13. Busch, G., Junod, P. and Wachter, P. (1964) Optical Absorption of Ferro- and Antiferromagnetic Europium Chalcogenides. Physics Letters, 12, 11-12.
http://dx.doi.org/10.1016/0031-9163(64)91155-2 - 14. Busch, G. and Wachter, P. (1966) Einfluß der magnetischen Ordnung auf die optische Absorption von ferro-oder antiferromagnetischen Halbleitern. Physik der kondensierten Materie, 5, 232-242.
- 15. Urban, P., Davidov, D., Elschner, B., Piefka, T. and Sperlich, G. (1975) Narrowing Effects in the ESR Spectra of Gd in Metals: Application to LaSb:Gd. Physical Review B, 12, 72.
http://dx.doi.org/10.1103/PhysRevB.12.72 - 16. Petit, L., Tyer, R., Szotek, Z., Temmerman, W.M. and Svane, A. (2010) Rare Earth Monopnictides and Monochalcogenides from First Principles: Towards an Electronic Phase Diagram of Strongly Correlated Materials. New Journal of Physics, 12, 113041-113061.
http://dx.doi.org/10.1088/1367-2630/12/11/113041 - 17. Neckel, A., Rastl, P., Eibler, R., Weinberger, P. and Schwarz, K. (1976) Results of Self-Consisted Band-Structure Calculations for ScN, ScO, TiC, TiN, VC, VN and VO. Journal of Physics C, 9, 579-592.
- 18. Monnier, R., Rhyner, J., Rice, T.M. and Koelling, D.D. (1985) Electron-Hole Liquid as a True Ground State. Physical Review B, 31, 5554-5556.
http://dx.doi.org/10.1103/PhysRevB.31.5554 - 19. Harbeke, G., Meier, E. and Dismukes, J.P. (1972) Electron Effective Mass in ScN. Optics Communications, 4, 335-338.
http://dx.doi.org/10.1016/0030-4018(72)90071-5 - 20. Travaglini, G., Marabelli, F., Monnier, R., Kaldis, E. and Wachter, P. (1968) Electronic Structure of ScN. Physical Review B, 34, 3876-3882.
http://dx.doi.org/10.1103/PhysRevB.34.3876 - 21. Dismukes, J.P., Yim, W.M. and Ban, V.S. (1971) Optical Properties of ScN. Proceedings of 3rd International Conference on Crystal Growth, Marseille, 536-538.
- 22. Wachter, P. (1972) The Optical Electrical and Magnetic Properties of the Europium Chalcogenides and the Rare Earth Pnictides. CRC Critical Reviews in Solid State Sciences, 3, 189-241.
- 23. Busch, G., Junod, P., Vogt, O. and Hulliger, F. (1963) Ferro- and Metamagnetism of Rare Earth Compounds. Physics Letters, 6, 79-80.
http://dx.doi.org/10.1016/0031-9163(63)90228-2 - 24. Busch, G., Vogt, O. and Schwob, P. (1967) Les Champs Magnétiques Intenses. CNRS (Colloques International du Centre National de Research Scientifique) No. 166, 401-407.
- 25. Junod, P., Menth, A. and Vogt, O. (1969) Revue des Propriétés Magnétiques et électroniques des Composés des Terres Rares avec les Anions du 5ième Groupe du Système Périodique. Physik der kondensierten Materie, 8, 323-370.
- 26. McGuire, T.R., Gambino, S.J., Pickart, S.J. and Alperin, H.A. (1969) Magnetic Structure and Exchange Interac-tions in Cubic Gadolinium Compounds. Journal of Applied Physics, 40, 1009-1010.
http://dx.doi.org/10.1063/1.1657506 - 27. Gambino, R.J., McGuire, T.R., Alperin, H.A. and Pickart, S.J. (1970) Exchange Interaction in GdN. Journal of Applied Physics, 41, 933-934.
- 28. Li, D.X., Haga, Y., Shida, H. and Suzuki, T. (1994) Magnetic Properties of Ferromagnetic GdN. Physica B, 199-200, 631-633.
http://dx.doi.org/10.1016/0921-4526(94)91928-3 - 29. Wachter, P. and Kaldis, E., Solid State Commun. (1980) Magnetic Interaction and Carrier Concentration in GdN and GdN1-xOx. Solid State Communications, 34, 241-244.
http://dx.doi.org/10.1016/0038-1098(80)90401-9 - 30. Wachter, P. and Kaldis, E. (1980) Magnetic Interaction in GdN and GdN1-xOx. Journal of Magnetism and Magnetic Materials, 15-18, 305-306.
http://dx.doi.org/10.1016/0304-8853(80)91062-8 - 31. Wachter, P. (2012) Physical Properties of Stoichiometric GdN Single Crystals. Results in Physics, 2, 90-96.
http://dx.doi.org/10.1016/j.rinp.2012.07.003 - 32. Leuenberger, F., Parge, A., Felsch, W., Fauth, K. and Hessler, M. (2005) GdN Thin Films: Bulk and Local Electronic and Magnetic Properties. Physical Review B, 72, Article ID: 014427.
http://dx.doi.org/10.1103/PhysRevB.72.014427 - 33. Hasegawa, A. and Yanase, A. (1977) Energy Band Structure of Gd Pnictides. Journal of the Physical Society of Japan, 42, 492-498.
http://dx.doi.org/10.1143/JPSJ.42.492 - 34. Wachter, P. (1978) Electronic Structure, Magnetic Exchange and Electrical Transport Properties of the Magnetic Compounds EuS, GdS and GdP. Physics Reports, 44, 159-186.
http://dx.doi.org/10.1016/0370-1573(78)90001-7 - 35. Campagna, M., Wertheim, G.K. and Baer, Y. (1979) Unfilled Inner Shells: Rare Earths and Their Compounds. In: Ley, L. and Cardona, M., Eds., Topics in Applied Physics, Vol. 27, Photoemission in Solids II, Case Studies, Springer Verlag, Berlin, 217-260.
- 36. Kasuya, T. and Yanase, A. (1968) Anomalous Transport Phenomena in Eu Chalcogenide Alloys. Reviews of Modern Physics, 40, 684-695.
http://dx.doi.org/10.1103/RevModPhys.40.684 - 37. Li, D.X., Haga, Y., Shida, H., Suzuki, T. and Kwon, Y.S. (1996) Electrical Transport Properties of Semimetallic GdX Single Crystals (X=P, As, Sb and Bi). Physical Review B, 54, 10483-10491.
http://dx.doi.org/10.1103/PhysRevB.54.10483 - 38. Berton, A., Chaussy, J. and Veyssie, J.J. (1966) Ann. Acad. Sci. Fennicae A. VI., 210, 233.
- 39. Stutius, W. (1969) Spezifische Warme der Nitride Seltener Erden. Physik der Kondensierten Materie, 10, 152-185.
- 40. Schlegel, A. (1979) Optical Properties and Electronic Structure of Some Rare Earth Monopnictides. Thesis, ETH Zürich, Zürich.
- 41. Wachter, P. (1964) Messung der optischen Absorption an Ferround Antiferromagnetischen Verbindungen Seltener Erden. Helvetica Physica Acta, 37, 637.
- 42. The Author Is Very Grateful to Dr. N. Zhigadlo, Lab. für Festkorperphysik, ETH Zürich, Switzerland, for This Measurement.
- 43. Goodenough, J.B. (1963) Magnetism and the Chemical Bond. Interscience Monographs on Chemistry, Vol. I, John Wiley, New York 1-385.
- 44. Wachter, P., Kaldis, E. and Hauger, R. (1978) Magnetic Exchange Interaction in the System GdP-GdS. Physical Review Letters, 40, 1404-1407.
http://dx.doi.org/10.1103/PhysRevLett.40.1404 - 45. Bommeli, F., Degiorgi, L. and Wachter, P. (1995) Optical Properties of TbN. Journal of Magnetism and Magnetic Materials, 140-144, 1159-1160.
http://dx.doi.org/10.1016/0304-8853(94)00753-5 - 46. Kaldis, E., Schlegel, A., Wachter, P. and Zürcher, Ch. (1976) Electronic Structure of Divalent-, Trivalent- and Mixed Valent Rare Earth Compounds. Journal of Magnetism and Magnetic Materials, 3, 1-3.
- 47. Klaase, J.C.P. (1998) Private Communication. Natuurkundig Laboratorium, University of Amsterdam, Amsterdam.
- 48. Degiorgi, L., Teraoka, S., Compagnini, G. and Wachter, P. (1993) Optical and Raman Investigation of Yb Pnictide Compounds. Physical Review B, 47, 5715-5720.
http://dx.doi.org/10.1103/PhysRevB.47.5715 - 49. Degiorgi, L., Bacsa, W. and Wachter, P. (1990) Electronic Structure of YbN. Physical Review B, 42, 530-539.
http://dx.doi.org/10.1103/PhysRevB.42.530 - 50. Wouilloud, E. (1986) Thesis, University of Neuchatel, Neuchatel.
- 51. Mendik, M. and Wachter, P. (1993) Brillouin Scattering from Single Crystals YbX (X = N,P,As). Physical Review B, 47, 6110-6113.
http://dx.doi.org/10.1103/PhysRevB.47.6110 - 52. Ott, H.R., Rudigier, H. and Hulliger, F. (1985) Low-Temperature Phase Transitions in Yb Monopnictides. Solid State Communications, 55, 113-116.
http://dx.doi.org/10.1016/0038-1098(85)90259-5 - 53. Wachter, P. (1994) Intermediate Valence and Heavy Fermions. In: Gschneidner Jr., K.A., Eyring, L., Lander, G.H. and Choppin, G.R., Eds., Handbook on the Physics and Chemistry of Rare Earths, Vol. 19, Lanthanides and Actinides: Physics—II, Ch. 132, North-Holland Publishing, Amsterdam, 177-382.
- 54. Takagi, S., Oyamada, A. and Kasuya, T.J. (1988) 31P NMR Studies of the Magnetically Ordered Heavy Electron Compound YbP. Journal of the Physical Society of Japan, 57, 1456-1465.
- 55. Didchenko, R. and Gortsema, F.P. (1963) Some Electric and Magnetic Properties of Rare Earth Monosulfides and Nitrides. Journal of Physics and Chemistry of Solids, 24, 863-870.
http://dx.doi.org/10.1016/0022-3697(63)90062-3 - 56. Danan, J., de Novion, C. and Lallement, R. (1969) Proprietes Magnetiques Du Nitrure De Cerium: Centre d’Etudes Nucléaires de Fontenayaux-Roses, S.E.C.P.E.R., Section d’Etudes des Céramiques à base de Plutonium. Solid State Communications, 7, 1103-1107.
http://dx.doi.org/10.1016/0038-1098(69)90494-3 - 57. Kaldis, E., Steinmann, B., Fritzler, B., Jilek, E. and Wisard, A. (1982) CeN: Phase Relationships and Enthalpies of Solution. In: McCarthy, G., Silber, H., Rhyne, J. and Kalina, F.M., Eds., The Rare Earths in Modern Science and Technology, Vol. 3, Plenum Publishing Corp., New York, 227-236.
- 58. Baer, Y. and Zürcher, Ch. (1977) Electronic Structure of CeN Studied by X-Ray—Photoemission Spectroscopy. Physical Review Letters, 39, 956-959.
http://dx.doi.org/10.1103/PhysRevLett.39.956 - 59. Wuilloud, E., Delley, B., Schneider, W.D. and Baer, Y. (1985) Spectroscopic Study of Localized and Extended F-Symmetry States in CeO2, CeN and CeSi2. Journal of Magnetism and Magnetic Materials, 47-48, 197-199.
- 60. Patthey, F., Imer, J.M., Schneider, W.D., Beck, H., Baer, Y. and Delley, B. (1990) High Resolution Photoemission Study of the Low-Energy Excitations in 4f-Electron Systems. Physical Review B, 42, 8864-8881.
http://dx.doi.org/10.1103/PhysRevB.42.8864 - 61. Mattenberger, K. and Vogt, O. (1992) Magnetism of Monochalcogenides and Monopnictides of the Actinides. Physica Scripta T, 1992, 103.
http://dx.doi.org/10.1088/0031-8949/1992/T45/022 - 62. Stewart, G.R. (1984) Heavy Fermion Systems. Reviews of Modern Physics, 56, 755-787.
http://dx.doi.org/10.1103/RevModPhys.56.755 - 63. Delin, A., Oppeneer, P.M., Brooks, M.S.S., Kraft, T., Wills, J.M., Johansson, B. and Erikson, O. (1997) Optical Evidence of 4f-Band Formation in CeN. Physical Review B, 55, R10173-R10176.
http://dx.doi.org/10.1103/PhysRevB.55.R10173 - 64. Larson, P., Lambrecht, W.R.L., Chantis, A. and van Schilfgaarde, M. (2002) Electrical Properties of Rare Earth Nitrides Using the LSDA-U Approach: Importance of Allowing 4f Orbitals to Break the Cubic Crystal System. Physical Review B, 75, 045114-1-045114-14.
- 65. Kanchana, V., Vaitheeswaran, G., Zhang, X., Ma, Y., Svane, A. and Erikson, O. (2011) Lattice Dynamics and Elastic Properties of the 4f Electron System: CeN. Physical Review B, 84, 205135-1-205135-7.
http://dx.doi.org/10.1103/PhysRevB.84.205135 - 66. Landrum, G.A., Dronskowski, R., Niewa, R. and DiSalvo, F. (1999) Electronic Structure and Bonding in Cerium (Nitride) Compounds: Trivalent versus Tetravalent Cerium. Chemistry—A European Journal, 5, 515-522.
3.0.CO;2-Y>http://dx.doi.org/10.1002/(SICI)1521-3765(19990201)5:2<515::AID-CHEM515>3.0.CO;2-Y - 67. Litsarev, M.S., Di Marco, I., Thunstrom, P. and Erikson, O. (2012) Correlated Electronic Structure and Chemical Bonding of Cerium Pnictides and γ-Ce. Physical Review B, 86, 115116-1-115116-7.
http://dx.doi.org/10.1103/PhysRevB.86.115116 - 68. Marabelli, F., Travaglini, G. and Wachter, P. (1986) Electronic Structure of UPt3 in the Vicinity of the Fermi Energy. Solid State Communications, 59, 381-384.
http://dx.doi.org/10.1016/0038-1098(86)90567-3 - 69. Marabelli, F. and Wachter, P. (1990) Temperature Dependence of the Optical Conductivity of the Heavy-Fermion System CeCu6. Physical Review B, 42, 3307-3311.
http://dx.doi.org/10.1103/PhysRevB.42.3307 - 70. Marabelli, F. and Wachter, P. (1988) Far Infrared Optical Study of the Heavy Fermion CeCu6. Solid State Communications, 67, 931-934.
http://dx.doi.org/10.1016/0038-1098(88)90459-0 - 71. Marabelli, F. and Wachter, P. (1990) Optical Study of U2PTC2: Evidence of Heavy Fermion Behavior. Solid State Communications, 74, 1075-1078.
http://dx.doi.org/10.1016/0038-1098(90)90713-L - 72. Awasthi, A.M., Degiorgi, L., Grüner, G., Dalichaouch, Y. and Maple, M.B. (1993) Complete Optical Spectrum of CeAl3. Physical Review B, 48, 10692-10700.
http://dx.doi.org/10.1103/PhysRevB.48.10692 - 73. Gunnarson, O. and Schonhammer, K. (1983) Photoemission from Ce Compounds: Exact Model Calculation in the Limit of Large Degeneracy. Physical Review Letters, 50, 604-610.
http://dx.doi.org/10.1103/PhysRevLett.50.604 - 74. Martin, R.M. (1982) Fermi-Surface Sum Rule and Its Consequences for Periodic Kondo and Mixed Valence Systems. Physical Review Letters, 48, 362-365.
http://dx.doi.org/10.1103/PhysRevLett.48.362 - 75. Schlegel, A., Wachter, P., Nickl, J.J. and Lingg, H. (1977) Optical Properties of TiN and ZrN. Journal of Physics C: Solid State Physics, 10, 4889-4895.
http://dx.doi.org/10.1088/0022-3719/10/23/022 - 76. Schlegel, A., Kaldis, E., Wachter, P. and Zürcher, Ch. (1978) Optical Properties and Valence Mixing in CeN. Physics Letters A, 66, 125-128.
http://dx.doi.org/10.1016/0375-9601(78)90015-4 - 77. Wachter, P. and Zhigadlo, N.D. (2013) Physical Properties of Stoichiometric CeN Single Crystals. Results in Physics, 3, 235-240.
http://dx.doi.org/10.1016/j.rinp.2013.09.007





































