Advances in Materials Physics and Chemistry
Vol.3 No.2(2013), Article ID:32647,7 pages DOI:10.4236/ampc.2013.32016
Electrical Response of Silanization of Rubber Mixtures
1Department of Physics, Institute of Materials, Faculty of Materials Science, Slovak University of Technology, Trnava, Slovak Republic
2Department of Physics, Faculty of Education, Catholic University, Ruzomberok, Slovak Republic
Email: emil.seliga@stuba.sk
Copyright © 2013 Emil Seliga et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 27, 2013; revised May 13, 2013; accepted May 21, 2013
Keywords: Silanization; Electrical Response; Chemical Kinetics; Rubber Mixture; Electrical Conductivity
ABSTRACT
There are a number of experimental methods aimed at the investigation of structural transformations. These methods differ from each other by a spectrum of quantitative indicators and their application is limited by the nature of investigated structures and processes. In a sense, it is also possible to consider the silanization of rubber mixtures as a structural transformation. Experimental observation of transformations of disordered rubber mixtures type structures can be quite difficult. The contribution deals with the theoretical principles of experimental methodology oriented on the investigation of silanization of rubber mixtures. We analyze the electrical response of rubber mixtures silanization. Our attention is focused on the modeling of a possible electrical response of a chemical reaction in a system consisting of several components. The results of the model are compared with experimental data measured during the silanization reaction in rubber mixtures.
1. Introduction
Rubber mixtures have already attracted the attention of material technologists for several decades. Relatively wide application possibilities of these materials are the reason of this fact, in particular, in the manufacture of tires. The preparation of the optimal combination of different fillers intended to rubber compounds, such as carbon black, rubber nibs, kaolin, silicon dioxide, titanium dioxide, talc, short fibers, or limestone, is in the centre of interest of tires producers.
Chemical additives for rubber mixtures preparation typically contain plasticizer (for example, polyethylenevinylalcohol and/or cellulose acetate), which is combined in a plasticized form with silica (SiO2) and/or carbon black. At the same time the binding agent is applied, most often silanes (for example SiH4). Application of silanes (silanization) is recommended in particular for the purpose of hydrofobization of silane-hydrophilic fillers such as silicon dioxide. It is assumed that chemically reactive silanes are able to react with hydroxyl groups in silicon dioxide, thus improve their compatibility with relatively low polar rubber matrix and eliminate the strong OH-OH interaction in the silicon dioxide. Possibilities for dispersion of silica in the matrix are improved in this way. The process of silanization is oriented to the networking and reinforcement of those components of the rubber mixture, which are filled with silane. The silanization significantly increases the strength of the bindings in the microstructure of materials and this strength is ultimately affected by the character of the silanization process.
The aim of our work is to analyze the possibility of monitoring of chemical kinetics of the process of silanization by means of measurements of electric parameters (electrical conductivity) of rubber blends directly in the process of its treatment. We assume that the silanization is chemical reaction and therefore it must obey to the laws of the chemical kinetics. Factors affecting the speed of a chemical reaction are analyzed by the theory of chemical reactions, which in general examine the chemical reaction progress. Changes of physical and chemical properties of the system occur during the chemical reaction.
The methodology based on analysis of the electrical response may be suitable for registration of specific forms of structural transformations that are accompanied by a generation (or recombination) of charge carriers in structure. If products (or intermediates) of chemical reaction are components of a different concentration of charge carriers other than the reactants entering to the reaction, it is possible to expect changes of electrical conductivity of reacting mixture. The question remains, to what extent this change corresponds of electric conductivity to the silanization reaction.
In our work we examine the process of silanization at the linear change of temperature of rubber mixtures. Continuous changes in temperature dependence of electrical conductivity of these mixtures corresponding to the silanization can be identified. We focus our attention on the modeling of temperature dependence of electrical conductivity of rubber compounds in the process of silanization on the basis of chemical kinetics equations.
2. Theory
Measurement of electric and dielectric constants is one of the important experimental techniques to study of structural and phase transformations. The electrical conductivity of rubber is caused by the presence of impurities that are able to realize the transport of ions in the structure of the material. However, the mechanism of electrical conductivity of rubber blends directly in the process of silanization, is not yet fully understood. Most models of transport mechanisms explaining the electrical conductivity are based on the analysis of the concentration of charge carriers in the material structure.
We analyze the changes of the electric conductivity of rubber blends during the silanization, provided that the changes of the concentration of charge carriers in the mixture obey equations of chemical kinetics. We consider silanization as a chemical reaction of first-order kinetics.
Rubber mixtures consist of multiple components. Suppose that the electrical conductivity of rubber mixtures during silanization may be determined by the sum:
 (1)
(1)
where  is the electric conductivity of components, which don’t participate in the silanization reaction and
is the electric conductivity of components, which don’t participate in the silanization reaction and 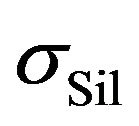 is a contribution of reactants to the resulting electrical conductivity of the rubber mixture
is a contribution of reactants to the resulting electrical conductivity of the rubber mixture . We expect that contributions on the right side of the Equation (1) obey the Arrhenius relation [1,2]:
. We expect that contributions on the right side of the Equation (1) obey the Arrhenius relation [1,2]:
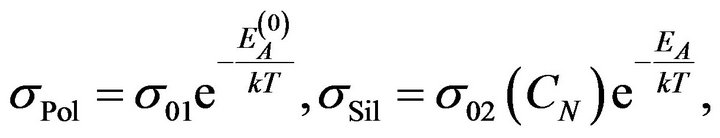 (2)
(2)
where k is Boltzmann's constant and T is the thermodynamic temperature. Activation energy of charge carriers in the components, which not participate in the silanization  may not be the same as the activation energy in reactants
may not be the same as the activation energy in reactants .
.
Within the model we assume that two components of the mixture are participating in the silanization reaction while change of the concentration of one of them is dominant. Suppose that pre-exponential factor  is directly proportional to the concentration CN of component mentioned above, i.e.:
is directly proportional to the concentration CN of component mentioned above, i.e.:
 (3)
(3)
where  is a constant. It is necessary to know how the concentration CN changes during the reaction for the determination of s02.
is a constant. It is necessary to know how the concentration CN changes during the reaction for the determination of s02.
If we start from the equation of chemical reactions of first-order kinetics, then for the concentration applies [3]:
 (4)
(4)
where cr is the rate constant of chemical reaction that depends on the temperature T and also must satisfy the Arrhenius relation [4,5]:
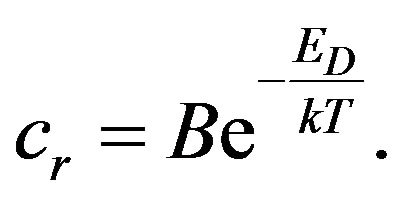 (5)
(5)
ED is the activation energy of a chemical reaction and B is a constant. If we take into account the time dependence of the temperature of the rubber mixture, for the change of the concentration CN we get:
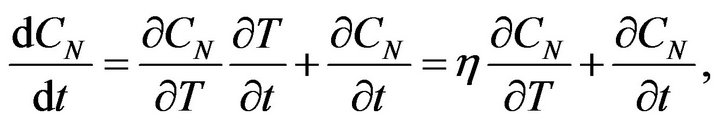 (6)
(6)
where h is the rate of the system temperature change. In the case if the temperature of system is increasing linear:
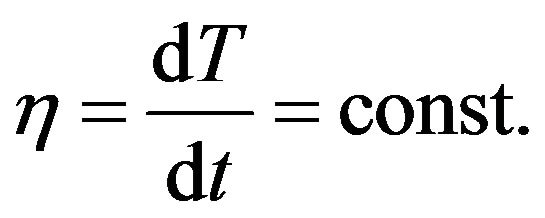 (7)
(7)
Considering (6) and (4) we get the equation:
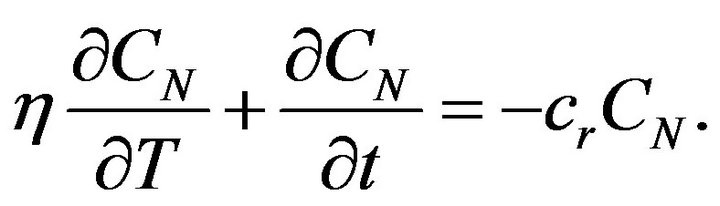 (8)
(8)
Equation (8) can be solved by separation of variables and solution can be written in the next form:
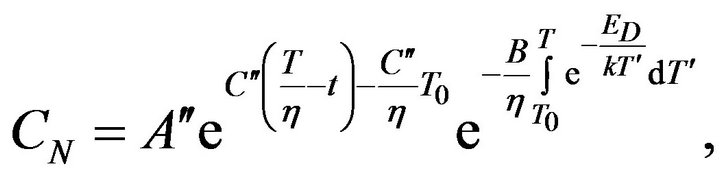 (9)
(9)
where  and
and  are constants. T0 is the initial temperature of the mixture. Considering (7) we can change of the temperature of system determine by next formula:
are constants. T0 is the initial temperature of the mixture. Considering (7) we can change of the temperature of system determine by next formula:
 (10)
(10)
where b is a constant. Then the first member in the exponent in formula on the right side of the (9) can be expressed as follows:
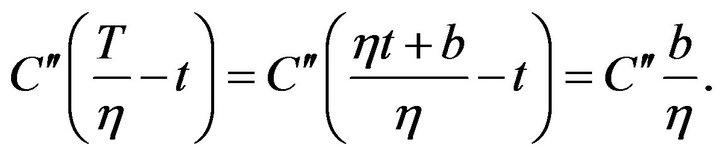 (11)
(11)
Temperature dependence of the concentration CN in the case of the linear change of temperature is:
 where
where  (12)
(12)
The factor 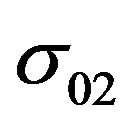 we determine by substituting (12) into (3):
we determine by substituting (12) into (3):
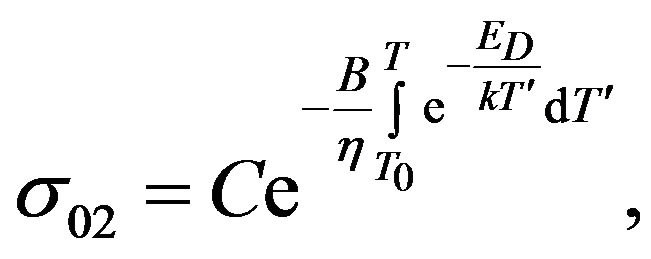 where
where 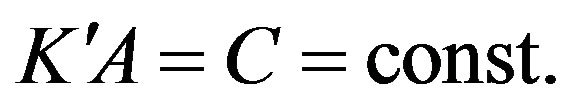 (13)
(13)
Subsequently, taking account of the previous result (13) in (2), it is possible to find a contribution of the reactant to the electrical conductivity of mixture sSil:
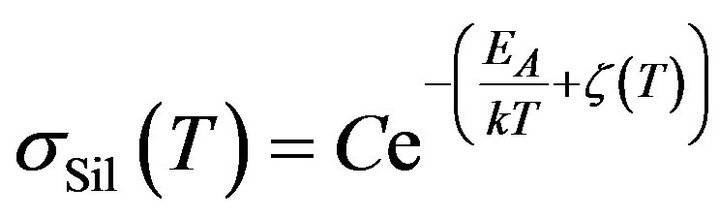 where
where 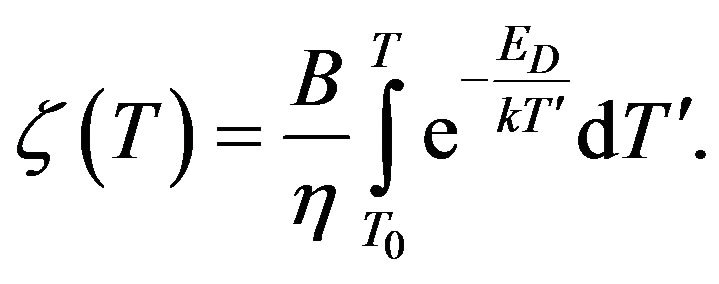 (14)
(14)
Formula (14) determine the temperature dependence of the electrical conductivity of such component in the mixture that is directly associated with the process of silanization. The result is correct if the temperature of mixture rise proportionally to time.
The integral on the right side of Equation (14) can be solved using the substitution:
 (15)
(15)
and subsequently, it take the next form:
 (16)
(16)
Since the integral in (16) cannot be solved analytically, in order to verification of the result we can make fractional polynomial approximation of integrated function by means of Taylor series in the point u = 0:

and exponent in the right side of (14) can be determined as follows:
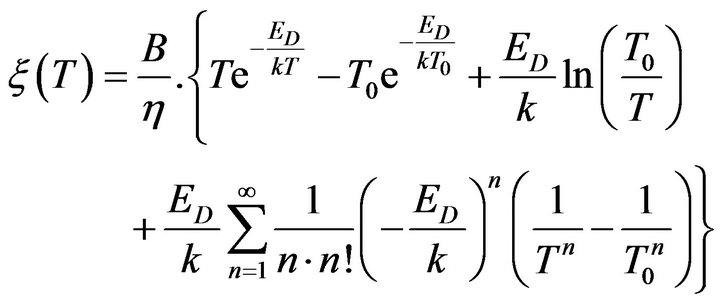 . (17)
. (17)
Then if we substitute (17) to (14) we can determine the electric conductivity of reactants in mixture in the next form:
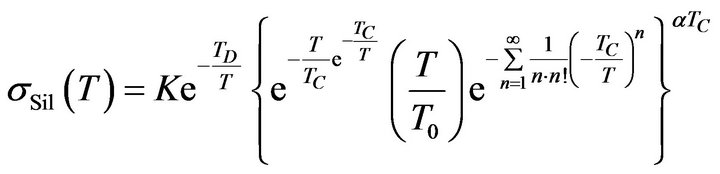 where:
where: (18)
(18)
and K is a constant. The sum in the exponent in Formula (18) converges for each  according to the Leibnitz criteria. Therefore the result is applicable at the modeling of temperature dependencies of electrical conductivity of rubber mixtures directly in the process of silanization assuming a linear change of temperature of rubber mixture.
according to the Leibnitz criteria. Therefore the result is applicable at the modeling of temperature dependencies of electrical conductivity of rubber mixtures directly in the process of silanization assuming a linear change of temperature of rubber mixture.
3. Discussion
The process of silanization is relatively complicated chemical reaction and its evaluation in terms of both the chemical and the application, requires complex analytical methods. Theoretical model by means of which it is possible to establish a methodology suitable for monitoring of rubber mixtures silanization by using its electrical response has been described in previous chapter. The model is based on the assumption that the temperature dependence of the electric conductivity of rubber mixture during silanization can be estimated using the Formula (1). We have got the result (18), provided that the silanization is chemical reaction of the first-order kinetics and only two components of the rubber mixture participate in the chemical reaction. On the basis of the result (18) it is possible to conclude under what conditions (and if at all) the temperature dependence of the electric conductivity of mixture allows investigate and evaluate the process of silanization.
In the analysis of the sSil(T) it is necessary to consider such temperatures T, in which the macroscopically observable effects of silanization can be identified in system. Therefore we assume that the mean value of the energy of thermal movement of molecules in reactive components of the system is much greater than the activation energy of a chemical reaction ED in (5). We suppose that mentioned assumption can be formulated as follows:
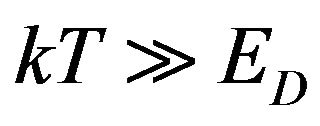 (19)
(19)
and it can be applied in the polynomial approximation (17) (u = 0 was considered in this approximation and  just in case (19)). With regard to the notation in (18), Formula (19) shows that we need to consider temperatures
just in case (19)). With regard to the notation in (18), Formula (19) shows that we need to consider temperatures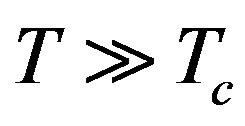 , i.e.:
, i.e.:
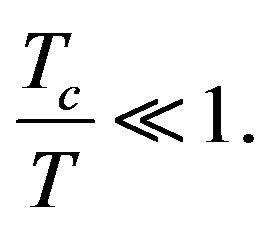 (20)
(20)
Tc is the temperature at which the silanization reaction begins. On the basis of (20) it is possible to conclude that in the estimating the temperature dependence of sSil(T) only the first member in sum in the exponent in (18) we need to consider in first approximation (i.e. the member corresponding to n = 1). All other members (i.e. n > 1) can be neglected for the simplicity.
In view of the nature of the electrical response of silanization it is important to analyse the character of function sSil(T). Temperature dependence of the silanization component of electrical conductivity (18) has in first approximation extreme in case, if there is such temperature Tm, which satisfies next equation (assuming that sSil(T) is different from zero):
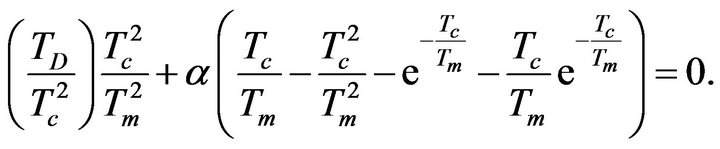 (21)
(21)
The existence of solutions of the previous Equation (21) guarantees that the temperature dependence of sSil(T) exhibits extreme at a certain temperature. Then the character of extreme can be determined by means of sign of the second derivative of the function (28) for T = Tm:
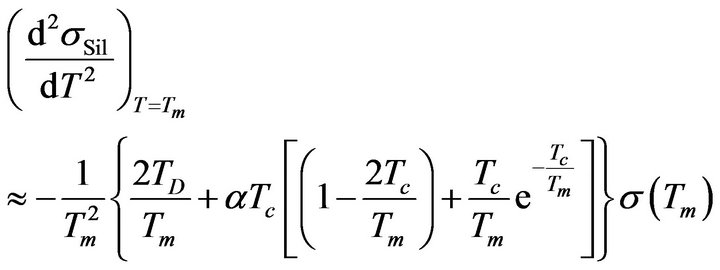 . (22)
. (22)
Validity of Equation (21) is considered in Formula (22). If we have the substitution:
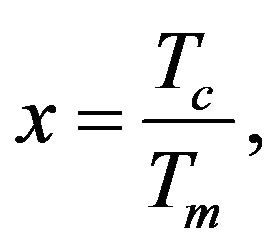 (23)
(23)
it is possible to transform the Equation (21) by using substitution (23) to the next form:
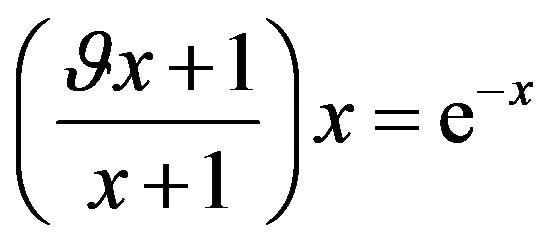 , where
, where 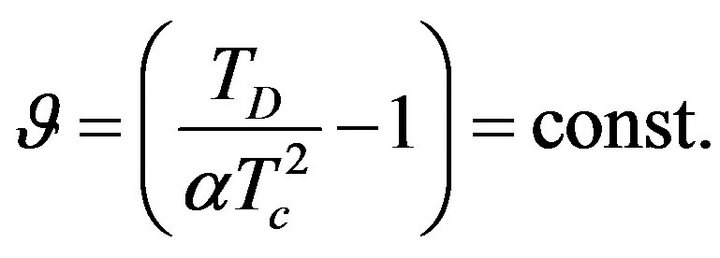 (24)
(24)
Then the problem of the extreme of function sSil(T) can be solved graphically. The solution of the Equation (24) exists in case if graphs of functions on the left and right side of the equation intersect. Let us denote the function on the left side of the Equation (24) by symbol f(x). Graphs of functions f(x) for various values of the constants  and graph of the function e−x are shown in Figure 1. In view of the (20) we are interested only in such solutions of the Equation (24) which fall within the range
and graph of the function e−x are shown in Figure 1. In view of the (20) we are interested only in such solutions of the Equation (24) which fall within the range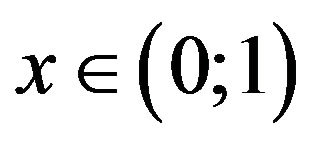 .
.
From Figure 1 it can be understood that graphs intersect only in cases if the constant  is greater or equal than its certain boundary value
is greater or equal than its certain boundary value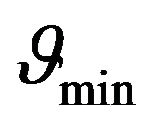 . Boundary value
. Boundary value 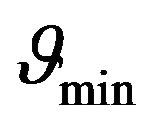 can be easy determined when we will substitute x = 1 to the Equation (24):
can be easy determined when we will substitute x = 1 to the Equation (24):
 (25)
(25)

Figure 1. Graphs of functions on both sides of the Equation (24).
Then from (25) we get:
 (26)
(26)
Constant  is determined by (24) and from the foregoing considerations it is clear that the temperature dependence of sSil(T) exhibits extreme only in the case if:
is determined by (24) and from the foregoing considerations it is clear that the temperature dependence of sSil(T) exhibits extreme only in the case if:
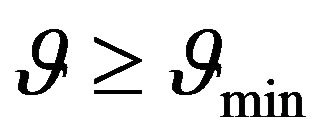 (27)
(27)
It is possible to determine such value of variable x which satisfies the Equation (24) from the graphs intersection in Figure 1. Then using (23) we can easy determine the temperature Tm at which the temperature dependence sSil(T) has extreme:
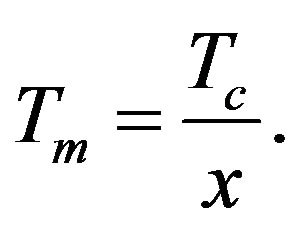 (28)
(28)
If we consider facts mentioned above it is clear that Formula (22) can be written in the next form:
 (29)
(29)
Values of a and Tc are positive, electric conductivity s is also positive. From this it is clear that the sign of the second derivative (29) is determined by value of the expression in parentheses on the right side of the equation. If we consider inequality (27), it is clear that:
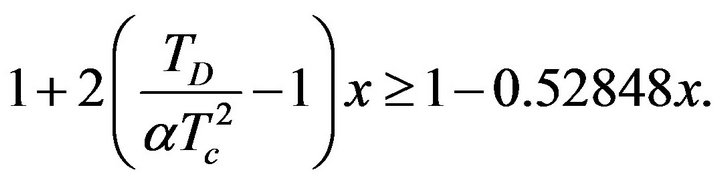 (30)
(30)
The value of (30) is positive for all x from the interval (0, 1). It is evident from this that the value of the second derivative of function sSil(T) for T = Tm is always negative. Therefore, the function of the sSil(T) exhibits always maximum at Tm.
Above results indicate that continuous change of the electric conductivity of rubber mixture can be expected during silanization. According (27) existence of the maximum in the temperature dependence of sSil(T) is influented by the linear increasing of heating rate.
4. Comparison with Experimental Data
In the last decade significant effort has been devoted to the experimental study of physical properties of disordered structures [6-14]. In general, less attention has been focused on the electric properties of rubber mixtures.
In our labs variety of rubber mixtures was prepared for the purpose of the experimental study of the silanization. Mixtures differed from each other by their composition. Temperature dependences of the AC electric conductivity of prepared rubber mixtures σ(T) were measured during the linear increasing of temperature (h = 1˚C∙min−1) in the temperature range from 30˚C up to 170˚C. Measurements were carried out using equipment GoodWill LCR 819 at the frequencies from 20 Hz to 100 kHz. Temperature dependencies of AC conductivity measured at all frequencies had the similar character. Results of these measurements are shown in Figure 2 (red points). Results of the model described above are also shown in Figure 2 (blue line) for the purpose of comparison.
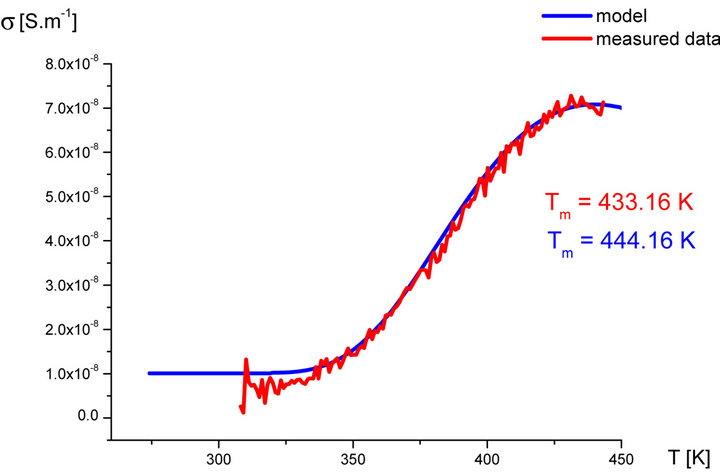
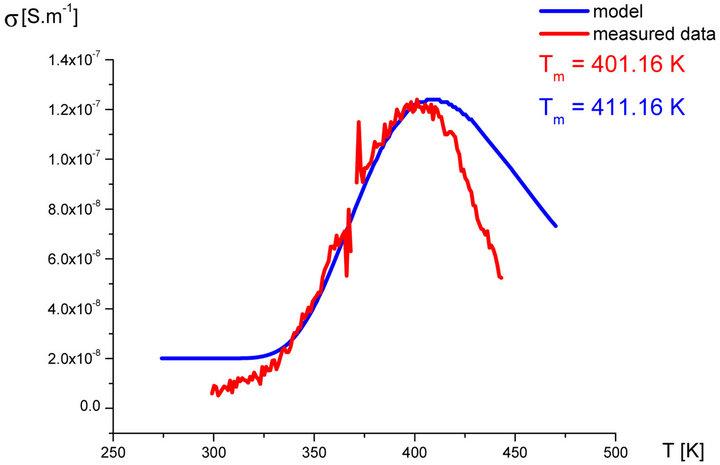



Figure 2. Temperature dependence of AC electrical conductivity s(T) at frequency 1 kHz of various silanization conditions of rubber mixture (measured data-red points, model-blue line).
It is clear that the temperature dependence of rubbermixture electric conductivity s(T) can really be considered to be superposition of electric conductivity generated by silanization components and electric conductivity of components, which don’t participate in the silanization reaction. Contribution of silanization to the electrical conductivity can be generated by the creation of charge carriers in the some of products of the silanization reaction. The existence of a local maximum in the temperature dependence s(T) has been always identified experimentally. This fact, which resulted from theoretical analysis described above, was confirmed by the results of experimental measurements.
As we can see from results values of electrical conductivity measured experimentally correspond to result of the theoretical model. This means that it is possible to choice such parameters of modeled functions sSil(T) that provide relevant results. But certain discrepancy was observed at temperatures T > Tm. At these temperatures the faster decrease of measured values of AC conductivity of mixture has been recorded experimentally than it was predicted by the model. The question is, what is the cause?
Presented model of charge transport in rubber mixtures is based on the effects of fluctuations of charge carriers concentration CN due to the chemical reaction. We assumed that there is well known simple relation between electrical conductivity and charge carriers concentration CN (see Equation (3))
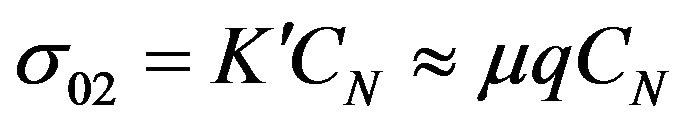 .
.
q is the electric charge of carriers and m is carriers mobility. The concentration CN is proportional to the total amount of charge in system and the charge carriers mobility m characterizes how quickly charge can move in the mixture, when an electric field is applied. Therefore the mobility is also a very important parameter affecting the electrical properties of mixtures. In general, almost always, higher mobility leads to higher electrical conductivity. One of the main factors determining the mobility of charge carriers is scattering time. The scattering time determine how long carriers are accelerated by the electric field until they collide in structure with something that changes their direction and energy.
It can be assumed that very important sources of the scattering in investigated rubber mixtures are transverse links formatted in microstructure during silanization. Density of crosslinking bonds in network increases during silanization reaction. The emerging transverse links generate scattering centers, cause the reduction of mobility and thus the reduction of electrical conductivity. We assume that because the effect of charge carriers scattering was not included in the proposed model slight discrepancy appears in the results.
5. Conclusion
We focused our attention on the theoretical model of the electric response of silanization of rubber mixtures. From the theoretical analysis we can conclude that the existence of local maximum in the temperature dependence of electrical conductivity of rubber mixtures can be expected during the process of silanization. That conclusion has been confirmed by the results of experimental measurements. Experimental data showed a peak in the temperature dependence of electrical conductivity. In addition, the peak was really identified in that temperature area where the most intense progress of silanization reaction might be expected. It can be concluded that equations of chemical kinetics can provide quite a good basis for the description of the electrical behavior of rubber mixture during the silanization. The potential impact of charge carriers scattering on the temperature dependence of the electric conductivity of rubber mixtures during silanization must be the subject of further research.
6. Acknowledgements
This research was supported by Slovak Grant Agency APVV under projects VEGA 1/0356/13, APVV-SK-CZ- 0168-11 and APVVSK-CZ-0195-11.
REFERENCES
- Z. H. Wang and H. Zhang, “Effective Activation Energy Ue(T,J,H) in Textured Bi1.84Pb0.4Sr2Ca2Cu3Oy Silver-Clamped Thick Films,” Physica C: Superconductivity, Vol. 320, No. 3-4, 1999, pp. 218-224. doi:10.1016/S0921-4534(99)00349-4
- M. Mizuno, H. Kokubo and K. Honda, “Preparation, Structure and Conduction Properties of SeCN-Containing Mixed Anion TTF Conductors,” Journal of Materials Chemistry, Vol. 11, No. 9, 2001, pp. 2192-2198. doi:10.1039/b101864g
- J. Hakl, “Over-Adiabatic Calorimetry (OAC),” Thermochimica Acta, Vol. 81, 1984, pp. 319-325. doi:10.1016/0040-6031(84)85137-0
- S. Srivastava, N. Metha, P. Agarval, D. Kumar and A. Kumar, “Thermal Characterization of Se100-xSbx Glasses Using Isoconversional Method,” Journal of Ovonic Research, Vol. 4, No. 6, 2008, pp. 147-157.
- B. Prochowska-Klisch and A. Malecki, Thermochimica Acta, Vol. 335, No. 1-2, 1999, pp. 99-104.
- P. Koštial, M. Mokryšová, J. Šišáková, Z. Mošková and S. Rusnáková, “A System to Measure both Inner and Outer Car Tire Temperatures ‘in Situ’,” International Journal of Thermophysics, Vol. 30, No. 1, 2009, pp. 334-340. doi:10.1007/s10765-008-0461-6
- S. Rusnáková, J. Slabeycius and V. Rusnák, “The Possibilities of Electronic Speckle Pattern Interferometry by Investigation of Composite Materials,” Proceedings of SPIE—The International Society for Optical Engineering, San Diego, 13-17 August 2006, 6p.
- D. Seidl, P. Koštial, Z. Jančíková, I. Ružiak, J. David, R. Puchký and I. Kopal, “Complex Contactless Flash Thermal Analyser of Low Conductive Materials,” Proceedings of the 13th International Carpathian Control Conference, High Tatras, 28-31 May 2012, pp. 628-630.
- P. Koštial, Z. Jančíková, I. Ružiak, I. Kopal and P. Jonšta, “The Influence of Rubber Blend Aging and Sample Homogeneity on Heat Transport Phenomena,” Defect and Diffusion Forum, Vol. 312-315, 2011, pp. 183-186. doi:10.4028/www.scientific.net/DDF.312-315.183
- J. Ďurfinová, I. Capek, I. ChodáK, A. Liška, P. Koštial, M. Chromčíková, P. Počarovský, M. Lacko, et al., “Plasticizers Influence on Physicalmechanical Properties and DMTA of Rubber Mixtures—Part A,” Chemicke Listy, Vol. 105, No. 15, 2011, pp. s325-s327.
- Z. Jonšta, P. Koštial, I. Ružiak, P. Jonšta, J. Jurčiová, Z. Jančíková, J. David and I. Kopal, “Advanced Fillers Enhancing Thermal and Mechanical Properties of Rubber Blends,” Journal of Nano Research, Vol. 13, 2011, pp. 27-32. doi:10.4028/www.scientific.net/JNanoR.13.27
- O. Bošák, J. Kalužný, J. Preto, J. Vacval, M. Kubliha and J. Hronkovič, “Electrical Properties of a Rubber Blend Used in the Tyre Industry,” Polymers for Advanced Technologies, Vol. 18, No. 2, 2007, pp. 141-143. doi:10.1002/pat.808
- S. Minárik, M. Kubliha, V. Labaš and J. Kalužný, “Computer Simulation of Alternate Conductivity of Polymer System,” Journal of Optoelectronics and Advanced Materials, Vol. 8, No. 4, 2006, pp. 1524-1528.
- M. Kubliha, “Investigating Structural Changes and Defects of Non-Metallic Materials via Electrical Methods,” Forschungszentrum Dresden-Rossendorf, Dresden, 2009.

