Advances in Materials Physics and Chemistry
Vol. 2 No. 3 (2012) , Article ID: 23196 , 5 pages DOI:10.4236/ampc.2012.23019
Magnetic Properties of Y3−2xCa2xFe5−xVxO12 Garnets
1Department of Physics, Sultan Qaboos University, Muscat, Sultanate of Oman
2Department of Physics and Nebraska Center for Materials and Nanoscience, University of Nebraska-Lincoln, Lincoln, USA
Email: *ialomari@yahoo.com, ialomari@squ.edu.om
Received May 7, 2012; revised June 13, 2012; accepted June 20, 2012
Keywords: Yttrium iron garnets; Curie temperature; Saturation magnetization; Magnetic moment
ABSTRACT
A comprehensive study of the magnetic properties of Y3−2xCa2xFe5−xVxO12 (0 ≤ x ≤ 1) has been performed. The garnet ferrites samples were prepared by the ceramic technique, and X-ray diffraction analysis indicates the formation of single cubic phase. Vibrating sample magnetometry (VSM) and a superconducting quantum-interference device (SQUID) were used to measure the magnetic properties, especially the magnetization and thermo-magnetic behavior. The magnetization curves exhibit the typical characteristics of ferrimagnetic materials at both 4.2 K and at room temperature. The samples have a low coercivities (between 20 and 40 Oe) and saturation magnetizations as high as 36 emu/g at 4.2 K. The saturation magnetization decreases with V and Ca contents, reaching about 8 emu/g at 4.2 K (x = 1). For all samples, the saturation magnetization decreases with increasing temperature, whereas the Curie temperature increases for small values of x, from 557 K for x = 0 to a maximum of 590 K for x = 0.2. For larger values of x, it decreases and reaches 525 K for x = 1.0. The basic experimental trends reflect the occupancy of the tetrahedral 24d sites by vanadium in combination with the predominant intersublattice exchange constant Jad, although the nonzero magnetization at x = 1.0 indicates that about 10% of the substituted V atoms goes onto the octahedral 16a sites.
1. Introduction
Many ferrites are valued as soft-magnetic materials, because they combine good high-frequency dielectric properties with ferrimagnetic order. They are widely used in applications such as microwave devices, transformers, electric generators, bio-processing, and storage devices [1-8]. The properties of the ferrites can be tailored in different ways, especially by chemical substitutions and by controlling the preparation method [9-17]. This is important for element-strategic reasons, such as the need to replace rare-earth elements.
Ferrites crystallize in a variety of crystal structures, such as spinel, garnet, and magnetoplumbite. The yttrium iron garnets (YIG) has a cubic structure composed from 160 atoms with the general formula Y3A2B3O12, where Y ions occupy the 24c sites in the Wyckoff notation, Fe the octahedral 16a and tetrahedral 24d sites, and oxygen the 96h sites. YIG is a ferrimagnets where the Fe atoms on the octahedral sites couple antiferromagnetically to the Fe atoms on the tetrahedral sites (Jad < 0). The intrasublattice interactions Jaa and Jdd are less important [18], and there is no coupling to the 24c sublattice, because yttrium is a nonmagnetic rare earth. There are three tetraheral and two octahedral sizes per formula unit, corre-sponding to a net moment of [5 (3 − 2) µB] = 5 µB. The garnets are chemically very stable, have high Curie temperatures (about 500 to 550 K), high electrical resistivities, and low dielectric losses over a wide range of frequencies.
Various YIG substitutions have been investigated in the past. Kim et al. [19] studied the effects of substitution of Fe by Al on the crystallographic and magnetic properties of YIG garnet and found that Al prefers the 24dtetrahedral sites, and the lattice constant decreases linearly with increasing the Al concentration. They also found that the saturation magnetization for the parent compound is about 33 emu/g at room temperature and it decreases with increasing the Al concentration, at room temperature and at 77 K. Different studies for the substitution of Y by other elements such as Tb [9], Sm [10], Gd [16], Bi [17], and Ce [13], indicate that the saturation magnetization tends to decrease with decreasing Y content. Furthermore, these papers show that the saturation magnetization depends on the preparation method. Furthermore, nanoparticles having sizes between 30 nm to 70 nm exhibit a magnetization that decreases with decreasing particle size due to the surface-spin effects.
The objectives of the present work are to prepare a series of Y3−2xCa2xFe5−xVxO12 garnet ferrites (x = 0.2, 0.4, 0.6, 0.8, 1.0) between 0.0 and 1.0) and to study the magnetic properties of these garnet ferrites at different temperatures. In these ferrites each V5+ ion requires two Ca2+ ions for electrostatic compensation [20], and the amount of Y3+ ions required is considerably reduced compared with the tetravalent or trivalent ion substitution.
2. Experimental Methods
A series of Y3−2xCa2xFe5−xVxO12 garnet ferrites (x = 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0) samples were prepared by ceramic technique. First, the appropriate masses of Y2O3, CaO, Fe2O3, and V2O5 were grounded using an agate mortar, followed by wet-mixing in acetone for 1 hr. Second, the mixtures were dried and annealed at 1500˚C for 15 hrs, followed by mechanical milling for 1 hr. Finally, they were sintered at 900˚C for 8 hrs. The samples were characterized by powder x-ray diffraction using a Philips diffractometer with Cu-Ka radiation. The magnetic properties were measured by vibrating sample magnetometry (VSM) in magnetic fields of up to 13.5 kOe and in the temperature range 77 - 1000 K. A superconducting quantum-interference device (SQUID) was used in magnetic fields up to 70.0 kOe and in the temperature range 4.2 - 300 K. The correct cubic crystal structure has been confirmed by x-ray diffraction (XRD) analysis.
3. Results and Discussion
Figure 1 Shows a typical x-ray diffraction pattern for a representative sample of the Y3−2xCa2xFe5−xVxO12 garnet ferrites, with x = 0.2. All samples studied in this paper show similar XRD patterns with a shift in the peaks’ positions due to the increase in the lattice constant. All the pecks are indexed with the cubic crystal structure indicating a single cubic phase for all the concentrations.
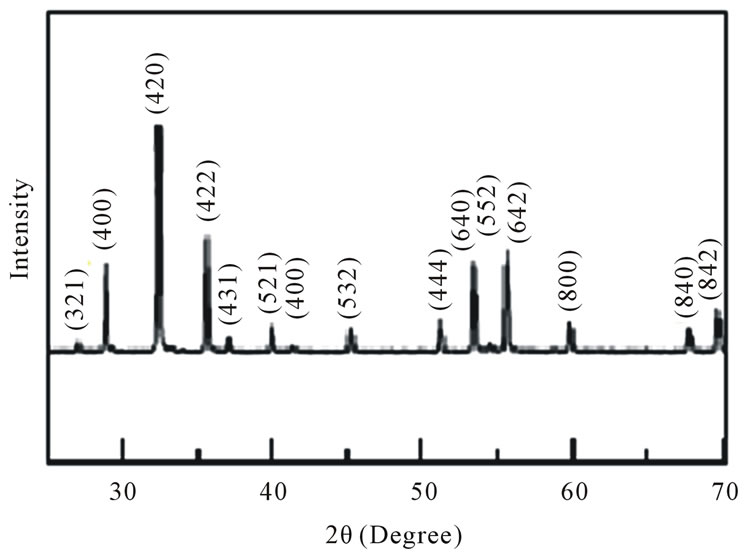
Figure 1. Typical x-ray diffraction pattern for a representative sample of the Y3−2xCa2xFe5−xVxO12 garnet ferrites, with x = 0.2.
Figure 2 shows the linear dependence of the lattice constant (a) on the concentration x, where a = (12.375 + 0.057x). The lattice constant for the parent compound (x = 0) is (12.375 ± 0.002) Å and it increases linearly with increasing concentration x, reaching (12.432 ± 0.002) Å for x = 1.0. This value for x = 0.0 is in good agreement with previous reported value of 12.381 Å by Kim et al. [21] for Y3Fe5O12 garnet ferrite.
Figure 3 shows the temperature dependence of the magnetization for the different Y3−2xCa2xFe5−xVxO12 samples in an applied magnetic field of 13.5 kOe. All samples order ferrimagnetically below the Curie temperature Tc. Using the method of intersecting tangents for the M vs. T curves we obtained the Curie temperatures for the different Y3−2xCa2xFe5−xVxO12 garnet ferrites. For small values of x, Tc increases from 557 K at x = 0, reaches a
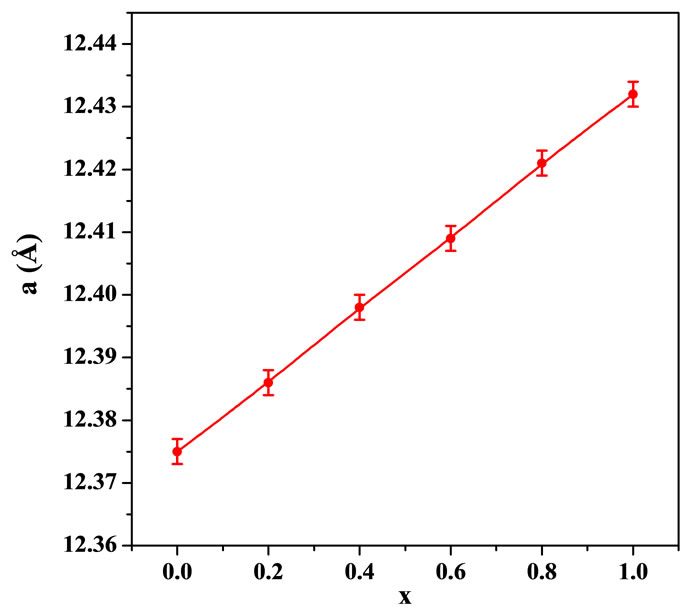
Figure 2. Dependence of the lattice constant (a) on the concentration (x) for Y3−2xCa2xFe5−xVxO12 garnet ferrites.

Figure 3. Temperature dependence of the magnetization for Y3−2xCa2xFe5−xVxO12 (x = 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0) in an applied magnetic field of 13.5 kOe. The inset shows the Curie temperature Tc as a function of the concentration x.
maximum of 590 K at x = 0.2, then decreases to 525 K at x = 1.0, as shown in the inset of Figure 3. Our Tc value of (557 ± 3) K at x = 0 is in agreement with previously obtained values of 550 K by Sanchez et al. [11] and Nimbore et al. [22], and of 560 K by Köbler and Hoser [23].
Figures 4 and 5 show the magnetization curves for the Y3−2xCa2xFe5−xVxO12 garnets at different temperatures, at 4.2 K and at 300 K. We see that the saturation magnetization decreases with increasing Ca and V concentrations. Furthermore, the saturation magnetization increases with decreasing temperature, as it is expected for a system with ferrimagnetic coupling below Tc. The samples show very low coercivities (between 20 Oe and 40 Oe), which is in agreement with previous results for similar ferrites Y3Fe5−xAlxO12 by Kim et al. [19]. Figure 6 summarizes the increase in the saturation magnetization with decreasing temperature and the decrease in Ms with increasing concentration x.
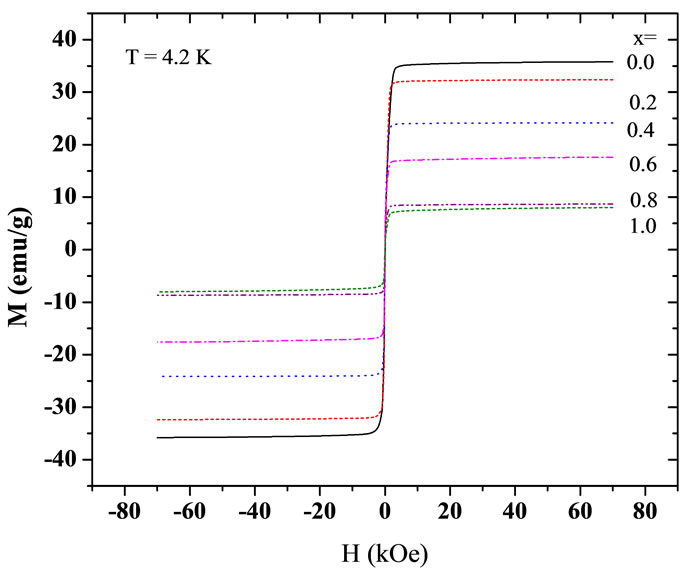
Figure 4. Low-temperature magnetization curves for Y3−2x Ca2xFe5−xVxO12 garnet ferrites at a temperature of 4.2 K.
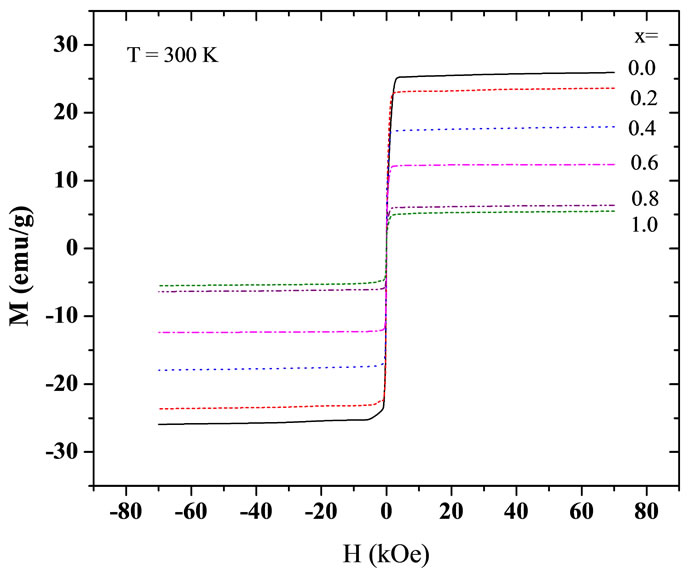
Figure 5. Room temperature magnetization curves for the Y3−2xCa2xFe5−xVxO12 garnet ferrites.
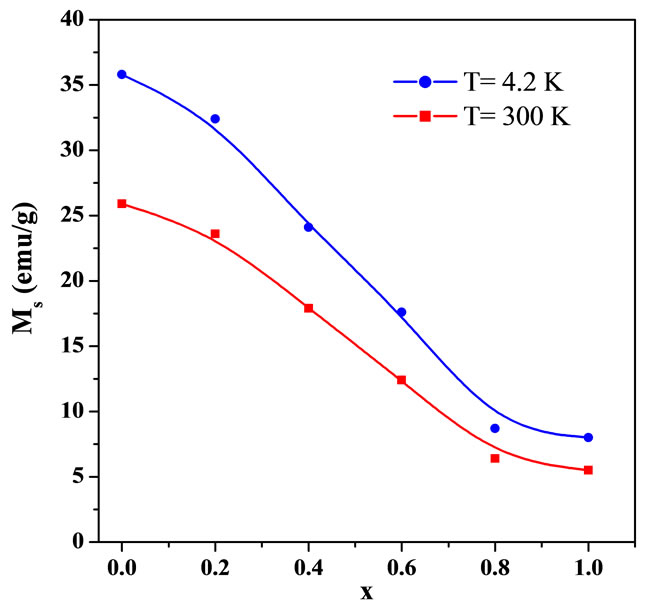
Figure 6. The saturation magnetization Ms of Y3−2xCa2xFe5−x VxO12 as a function of the concentration x at two temperatures (4.2 K and 300 K).
Garnets contain only trivalent ions; therefore no electron hopping occurs through the materials, leading to an extremely high resistivity and a low magnetic loss, even at high frequencies. Among the best ultrahigh frequencies (UHF) magnetic materials, single crystalline YIG has the narrowest resonance linewidth ΔH ≈ 0.1 G at 10 GHz [24]. Its saturation magnetization, temperature sensitivity and magnetocrystalline anisotropy can also be tuned by changing the compositions. In these garnet ferrites Y3+ ion (with a 4f0 electronic configuration) does not have a magnetic moment and Ca2+ (with a 4S0 electronic configuration) can be a substitution for Y3+ on dodecahedral sites and for the charge compensation. The substitution of Fe3+ ion by diamagnetic V5+ ion (with a 3d0 electronic configuration) improves the magnetic properties such as the Currie temperature and the optical properties such as Faraday rotation. The low magnetic loss in these ferrites is primarily attributed to the V5+ substitution for Fe3+ in the tetrahedral sites. A previous study for the substitution of Fe by (V and In) in the gadolinium garnet system GdzY3−2x−zCa2xFe2−yInyFe3−xVxO12 by Shinohara et al. [25] showed that V decreases the anisotropy constant (K1) which minimizes the ferromagnetic resonance linewidth and make the garnets as a suitable material for the microwave devices The reduced magnetization (x > 0) and the reduced Curie temperature (x > 0.2) reflect the occupancy of the tetrahedral 24d sites by vanadium, in combination with the predominant intersublattice exchange constant Jad. Mean-field theory predicts the Curie temperature to decrease as Tc(x) = Tc(0) (1 − x/3)1/2, because the Fe atoms on the octahedral sites have a reduced number of magnetic neighbors [26]. The initial increase in Curie temperature probably reflects structural distortions of the crystal lattice due to the substitution of the large Ca2+

Table 1. Dependence of the experimental low-temperature saturation magnetization, extrapolated to T = 0, on the Ca and V concentration x in Y3−2xCa2xFe5−xVxO12 garnet ferrites.
ions for Y3+ [27]. However, if all the V atoms went onto 24d sites, the magnetization would approach zero at x = 1.0. In the present case, there reamins a residual magnetization of 7.4 emu/g, as compared to 35.4 emu/g at x = 0, Table 1. This indicates that a certain fraction (about 10%) of the V goes onto the octahedral sites.
The flat shape of the M(T) curves is a consequence of the ferrimagnetic two-sublattice structure [28]. By solving the corresponding secular equations [26,29], one can show that the ratio of the two sublattice magnetizations is 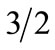 at low temperatures but
at low temperatures but  below Tc. This corresponds to a relative magnetization reduction of
below Tc. This corresponds to a relative magnetization reduction of  . For a one-sublattice ferromagnet, this ratio would be 1 and independent of temperature.
. For a one-sublattice ferromagnet, this ratio would be 1 and independent of temperature.
4. Conclusion
In this study, we were able to prepare Y3−2xCa2xFe5−xVxO12 garnets with less Y and Fe ions, with the same cubic structure and with higher Currie temperatures. The magnetic data in this paper indicate that the Y3−2xCa2xFe5−xVxO12 garnet ferrites is ferrimagnetically ordered for all the samples below Tc with the cubic structure being present up to the maximum Ca and V concentration x = 1.0. The samples exhibited very low coercivity (between 20 Oe and 40 Oe) with saturation magnetization (Ms), as high as ~36 emu/g (at 4.2 K). We also found that the saturation magnetization decreases with V and Ca contents reaching ~8 emu/g at 4.2 K. The obtained dependence of the Curie temperature and the saturation magnetization on the Ca and V concentration are due to the exchange interaction when Fe substituted by V, which increases the exchange interaction, and hence increases the Curie temperature for low x concentrations. All the results of the present work indicate homogenous solid solution when Y is substituted by Ca and Fe is substituted by V.
5. Acknowledgements
I. A. Al-Omari is grateful to Sultan Qaboos University for the support provided to perform this study under the research grant, number IG/SCI/PHYS/12/02. Research at Nebraska supported in part by NSF MRSEC Grant DMR-0820521.
REFERENCES
- R. L. Streever, “Anisotropic Exchange in ErIG,” Journal of Magnetism and Magnetic Materials, Vol. 278, No. 1-2, 2004, pp. 223-230. doi:10.1016/j.jmmm.2003.12.1231
- N. I. Tsidaeva, “The Magnetic and Magnetooptical Properties of Y-Substituted Erbium Iron Garnet Single Crystals,” Journal of Alloys and Compounds, Vol. 374, No. 1- 2, 2004, pp. 160-164. doi:10.1016/j.jallcom.2003.11.143
- Y. Nakata, T. Okada, M. Maeda, S. Higuchi and K. Ueda, “Effect of Oxidation Dynamics on the Film Characteristics of Ce:YIG Thin Films Deposited by Pulsed-Laser Deposition,” Optics and Lasers in Engineering, Vol. 44, No. 2, 2006, pp. 147-154. doi:10.1016/j.optlaseng.2005.03.003
- M. Laulajainen, P. Paturi, J. Raittila, H. Huhtinen, A. B. Abrahamsen, N. H. Andersen and R. Laiho, “BixY3−xFe5O12 Thin Films Prepared by Laser Ablation for Magneto-Optical Imaging of Superconducting Thin Films,” Journal of Magnetism and Magnetic Materials, Vol. 279, No. 2-3, 2004, pp. 218-223. doi:10.1016/j.jmmm.2004.01.081
- A. S. Lagutin, G. E. Fedorov, J. Vanacken and F. Herlach, “Magnetic Properties of Dysprosium-Ittrium Ferrite-Garnets in Pulsed Magnetic Fields at Low Temperatures,” Journal of Magnetism and Magnetic Materials, Vol. 195, No. 1, 1999, pp. 97-106. doi:10.1016/S0304-8853(98)01040-3
- S. A. Nikitov, “Nonlinearity: Magneto-Optic-Microwave Interactions. Towards New Devices,” Journal of Magnetism and Magnetic Materials, Vol. 196-197, 1999, pp. 400-403. doi:10.1016/S0304-8853(98)00776-8
- C. S. Tsai, “Wideband Tunable Microwave Devices Using Ferromagnetic Film-Gallium Arsenide Material Structures,” Journal of Magnetism and Magnetic Materials, Vol. 209, No. 1-3, 2000, pp. 10-14. doi:10.1016/S0304-8853(99)00634-4
- D. Cruickshank, “1 - 2 GHz Dielectrics and Ferrites: Overview and Perspectives,” Journal of the European Ceramic Society, Vol. 23, No. 14, 2003, pp. 2721-2726. doi:10.1016/S0955-2219(03)00145-6
- S. da S. Marins, T. Ogasawara and A. S. Ogasawara, “Terbium-Yttrium-Iron Garnet Revisited,” Journal of Alloys and Compounds, Vol. 436, No. 1-2, 2007, pp. 415- 420. doi:10.1016/j.jallcom.2006.11.114
- Z. J. Cheng and H. Yang, “Synthesis and Magnetic Properties of Sm-Y3Fe5O12 Nanoparticles,” Physica E, Vol. 39, No. 2, 2007, pp. 198-202. doi:10.1016/j.physe.2007.04.003
- R. D. Sanchez, C. A. Ramos, J. Rivas, P. Vaqueiro and M. A. Lopez-Quintela, “Ferromagnetic Resonance and Magnetic Properties of Single-Domain Particles of Y3Fe5O12 Prepared by Sol-Gel Method,” Physica B, Vol. 354, No. 1-4, 2004, pp. 104-107. doi:10.1016/j.physb.2004.09.028
- U. Kobler and A. Hoser, “First Order Spin Flop Transition in Yttrium Iron Garnet (YIG),” Solid State Communications, Vol. 142, No. 6, 2007, pp. 350-354. doi:10.1016/j.ssc.2007.02.041
- H. T. Xu and H. Yang, “Magnetic Properties of Y3Fe5O12 Nanoparticles Doped Bi and Ce Ions,” Materials and Manufacturing Processes, Vol. 23, No. 1, 2008, pp. 1-4. doi:10.1080/10426910701524212
- Z. Abbas, R. M. Al-habashi, K. Khalid and M. Maarof, “Garnet Ferrite (Y3Fe5O12) Nanoparticles Prepared via Modified Conventional Mixing Oxides (MCMO) Method,” European Journal of Scientific Research, Vol. 36, No. 2, 2009, pp. 154-160.
- S. H. Vajargah, H. R. M. Hosseini and Z. A. Nemati, “Preparation and Characterization of Yttrium Iron Garnet (YIG) Nanocrystalline Powders by Auto-Combustion of Nitrate-Citrate Gel,” Journal of Alloys and Compounds, Vol. 430, No. 1-2, 2007, pp. 339-343. doi:10.1016/j.jallcom.2006.05.023
- Z. J. Cheng, H. Yang, L. X. Yu, Y. M. Cui and S. H. Feng, “Preparation and Magnetic Properties of Y3Fe5O12 Nanoparticles Doped with the Gadolinium Oxide,” Journal of Magnetism and Magnetic Materials, Vol. 302, No. 1, 2006, pp. 259-262. doi:10.1016/j.jmmm.2005.09.015
- H. T. Xu, H. Yang, W. Xu and L. X. Yu, “Magnetic Properties of Bi-Doped Y3Fe5O12 Nanoparticles,” Current Applied Physics, Vol. 8, No. 1, 2008, pp. 1-5. doi:10.1016/j.cap.2007.04.002
- J. Wojtowicz, “High Temperature Susceptibility of Garnets: Exchange Interactions in YIG and LuIG,” Journal of Applied Physics, Vol. 33, No. 3, 1962, pp. 1257-1258. doi:10.1063/1.1728680
- C. S. Kim, B. K. Min, S. J. Kim, S. R. Yoon And Y. R. Uhm, “Crystallographic and Magnetic Properties of Y3Fe5−xAlxO12,” Journal of Magnetism and Magnetic Materials, Vol. 254-255, 2003, pp. 553-555. doi:10.1016/S0304-8853(02)00864-8
- J. E. Evetts, “Concise Encyclopedia of Magnetic and Superconducting Materials,” Pergamon Press, Oxford, 1992.
- C. S. Kim, Y. R. Uhm, S. B. Kim and J.-G. Lee, “Magnetic Properties of Y3−xLaxFe5O12 Thin Films Grown by a Sol-Gel Method,” Journal of Magnetism and Magnetic Materials, Vol. 215-216, 2000, pp. 551-553. doi:10.1016/S0304-8853(00)00217-1
- S. R. Nimbore, D. R. Shengule, S. J. Shukla, G. K. Bichile and K. M. Jadhav, “Magnetic and Electrical Properties of Lanthanum Substituted Yttrium Iron Garnets,” Journal of Materials Science, Vol. 41, No. 19, 2006, pp. 6460-6464. doi:10.1007/s10853-006-0365-4
- U. Köbler and A. Hoser, “First Order Spin Flop Transition in Yttrium Iron Garnet (YIG),” Solid State Communications, Vol. 142, No. 6, 2007, pp. 350-354. doi:10.1016/j.ssc.2007.02.041
- G. Mumcu, K. Sertel, J. L. Volakis, A. Figotin and I. Vitebsky, “RF Propagation in Finite Thickness Nonreciprocal Magnetic Photonic Crystals,” IEEE on Antennas and Propagation Society International Symposium, Vol. 2, 2004, pp. 1395-1398. doi:10.1109/APS.2004.1330447
- T. Shinohara, S. Takeda, Y. Matsumoto and Y. Noro, “Magnetic Properties of Polycrystalline Gadolinium Calcium Vanadium and Indium Substituted YIG,” IEEE Transactions on Magnetics, Vol. 11, No. 6, 1975, p. 1676- 1679. doi:10.1109/TMAG.1975.1058966
- R. Skomski, “Simple Models of Magnetism,” University Press, Oxford, 2008. doi:10.1093/acprof:oso/9780198570752.001.0001
- V. M. Yudin, S. A. Poltinnikov, O. B. Proskuryakov and N. N. Parfenova, “High Curie Points of Calcium-Vanadium Garnets,” Physics Letters A, Vol. 28, No. 7, 1969, pp. 483-484. doi:10.1016/0375-9601(69)90639-2
- R. Skomski, “Finite-Temperature Behavior of Anisotropic Two-Sublattice Magnets,” Journal of Applied Physics, Vol. 83, No. 11, 1998, pp. 6724-6726. doi:10.1063/1.367827
- J. S. Smart, “Effective Field Theories of Magnetism,” Saunders, Philadephia, 1966.
NOTES
*Corresponding author.

