Theoretical Economics Letters Vol.05 No.02(2015), Article ID:55137,9
pages
10.4236/tel.2015.52021
Notes on Economic Growth with Scale Effects: Is Depopulation Compatible with Growth?
Masao Nakagawa1, Asuka Oura2, Yoshiaki Sugimoto3*
1Graduate School of Social Sciences, Hiroshima University, Higashi Hiroshima, Hiroshima, Japan
2Graduate School of Economics, Osaka University, Toyonaka, Osaka, Japan
3Faculty of Economics, Kansai University, Suita, Osaka, Japan
Email: *sugimoto@kansai-u.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 February 2015; accepted 18 March 2015; published 27 March 2015
ABSTRACT
This research develops a simple theory to analyze the compatibility of depopulation and sustain- able growth. By introducing the scale effect of aggregate rather than average human capital, it shows that the economy may enter a sustainable growth path with fertility recovery, keeping away from a non-Malthusian poverty trap.
Keywords:
Scale Effect, Depopulation, Human Capital, Growth

1. Introduction
Over the last few decades, there has been a strand of theoretical literature studying the role of population in economic growth. One of its main arguments is that population expansion improves total factor productivity through various channels, including the increase in potential inventors (Kremer [1] ) and R&D activities (Romer [2] , Aghion and Howitt [3] ). The size of population is proposed as a key determinant for the level of output per worker, although its effect on the growth rate may vanish in the long run.1
Such theories typically build on the condition that population increases in size over time. Certainly, they can incorporate population aging as long as fertility rates are above replacement level.2 However, this restriction will not be appropriate for some advanced economies in the future. According to the United Nations ([6] , p. 11), the world between 2005 and 2010 has as many as 75 countries or areas whose total fertility levels are below replacement level. Germany, Italy, and Japan will enter the phase of population decline over the decades up to 2050 (ibid., pp. 61-62). Because depopulation would exert adverse effects on the growth process, it is not theoretically apparent whether these economies will sustain growth in the long run.
Existing studies are unsatisfactory in this respect. Although the possibility of sustainable growth against depopulation is demonstrated by Dalgaard and Kreiner [7] and Strulik [8] , they treat demographic factors exogenously and thus are silent about the potential interaction between the fertility decision and the living stand- ard. Taking this approach neglects the feedback effect of economic growth on population and fails to examine the possibility of population recovery.3
Equally important, it is questionable whether their result-steady growth in output per worker accompanied by permanent depopulation-should be interpreted as economic growth. These issues are not addressed even in a seminal work by Strulik et al. [10] , which would be the most relevant to the present paper. They aim to account for the past and future dynamics of an economy in which fertility decisions and private R&D activities are en- dogenous. Although the fertility rate they calibrate exhibits an upward recovery to replacement level, it is gene- rated by an exogenous parameter change in the development process. Furthermore, they omit the possibility of stagnation resulting from depopulation by taking the entrance to a persistent growth path as historically inde- pendent. The present paper, in contrast, conducts a global dynamic analysis to present the existence of a non- Malthusian, catastrophic poverty trap, toward which population keeps shrinking and productivity goes into a stall.
Motivated by these observations, this research offers a theoretical framework for analyzing the compatibility of economic growth with depopulation. It develops a simple and tractable dynamic model of an economy that exhibits the following features.4 First, households face a quantity-quality trade-off in child rearing. Fertility decline results from a rise in education investment or, alternatively, from a decline in parental income. Second, the amount of new technology is assumed to depend on the level of aggregate rather than average human capital. This formulation, along with the quantity-quality trade-off, implies that education investment does not nece- ssarily accelerate technological progress. Third, a rise in the technology level in turn augments skills by pro- viding new knowledge/ideas to the young generation.5
Under such circumstances, average human capital increases over time and thus aggregate human capital exhibits faster growth than working population. Consequently the initially depopulating economy may sustain growth away from the non-Malthusian poverty trap, depending on the initial conditions on technology and human capital. The associated income growth may ultimately push the average fertility above the replacement level. The possibility of the fertility recovery is confirmed by a numerical analysis.
2. The Model
The economy has a one-sector, overlapping-generations structure and operates over
an infinite discrete time horizon,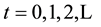 . It is small in size and open to global capital markets, where
the interest rate is stationary at
. It is small in size and open to global capital markets, where
the interest rate is stationary at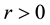 .
.
2.1. Firms
In perfectly competitive environments, firms generate a final good by employing
physical capital and human capital (i.e., labor in efficiency units). Let
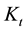 and
and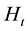 , respectively,
be the aggregate levels of these factor inputs in period t. Further, let
, respectively,
be the aggregate levels of these factor inputs in period t. Further, let
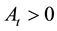 be the level of labor-augmenting technology in period t. Their relation- ship with
the level of aggregate output in period t,
be the level of labor-augmenting technology in period t. Their relation- ship with
the level of aggregate output in period t,
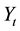 , is expressed
by a neoclassical production function F such that
, is expressed
by a neoclassical production function F such that
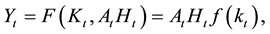 (1)
(1)
where
 and
and . The price
of the final good is normalized to unity. As a result of profit maximization by
price-taking firms,
. The price
of the final good is normalized to unity. As a result of profit maximization by
price-taking firms,
 and
and
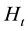 maximize the aggregate profit
maximize the aggregate profit
 , where
, where
 and
and
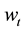 denote the rental price of physical capital and the wage rate per unit of efficiency
labor, respectively, in period t. For simplicity, physical capital is assumed not
to depreciate, so that the rental price equals the global interest rate r through
arbitration. Then, it follows that
denote the rental price of physical capital and the wage rate per unit of efficiency
labor, respectively, in period t. For simplicity, physical capital is assumed not
to depreciate, so that the rental price equals the global interest rate r through
arbitration. Then, it follows that
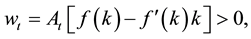 where
where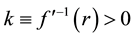 .
.
2.2. Households
A new generation is born at the beginning of each period and lives for three periods.
Generation t, born in period

Consider the lifetime of an individual of generation t. In the first period, the
individual engages in skill acqui- sition possibly with parental support. In the
second period, he/she acquires







The utility of an individual of generation t,




where

The level of efficiency units of labor hinges on two factors: the levels of education and technology. Human capital is augmented by technology, which embodies knowledge and ideas, on the grounds that their availability improves the efficiency of education. This is referred to as the skill-augmenting effect. The formation of human capital is formulated as

where




As price takers, parents maximize their own utility by allocating resources between consumption, the quantity of children, and education for them. Substituting Equations (2) and (4) into Equation (3), the maximization problem faced by a member of generation t becomes

subject to

In terms of

implying that

Substitution of Equation (6) into Equation (5) reveals that the necessary and sufficient
condition for an in- terior solution


noting that




where

2.3. Aggregate Human Capital and Technological Progress
The working population in period




where






As mentioned in the introduction, the present model abstracts from microeconomic
foundations that account for the innovation process. Suppose that the creation of
new technology is a by-product of manufacturing final output and depends on the
level of aggregate rather than average human capital, on the ground that more skilled
labor would come up with more ideas. Specifically,



where

Equations (9) and (10) constitute a two-dimensional, first-order autonomous system
for







3. The Dynamical System
This section explores the joint evolution of technology and aggregate human capital.
As will be apparent, the initial condition on


First, as follows from Equations (9) and (10),

Second, Equation (10) reveals that for any
Third and finally, Equation (9) reveals that for any

where






Proposition 1 clarifies two sufficient conditions on
Proposition 1. Under Equation (A1),

where

Proof. See Appendix A.
The phase diagram in Figure 1 graphically represents
the properties of the dynamical system derived thus far. The upper and lower boundaries
of the shaded area are the sets of




Any initial pair





Figure 1. Global Dynamics
of Technology and Human Capital. Notes: The diagram depicts the dynamical system
on


analytically ambiguous when the economy launches on the shaded area.
4. Analyses
4.1. The Hurdle to Sustainable Growth
As shown above,






Either a decrease in







4.2. Growth and Depopulation
This subsection investigates population dynamics underlying the growth process.
In line with Equation (17) in Strulik et al. [10] , aggregate human capital




where




In view of Equations (4) and (8), the dynamic behavior of


The complementary relationship in Equation (A2) generates a stimulative effect of technological progress on education investment; that is to say,14

These results, along with Equation (11) showing monotonic technological progress,
reveal that



Thus, working population decreases as long as aggregate human capital decreases,
or equivalently, as long as




While Equation (16) indicates the possibility of initial depopulation on an explosive
path, it is not apparent whether or not such a demographic trend continues. One
certain fact from Equation (14) is that the onset of population expansion is inevitable
if average human capital

4.3. The Dynamic Trend in Fertility
As mentioned earlier, it is generally not clear whether or not


Given Equation (15), a change in




A quantitative prediction of fertility is depicted in Figure 2, where one time period equals 30 years. The observed recovery to replacement level occurs under the following conditions. First, the production function of human capital is specified as

where




Figure 2. A Quantitative Prediction of Fertility.


Under these circumstances, the initial level of average fertility is

5. Concluding Remarks
The growth theory developed above has demonstrated that in the presence of a scale effect of human capital, the initial conditions on technology, population, and human capital determine whether an economy undergoing depopulation enters a steady-growth path, along which population growth may ultimately turn positive. The possibility of falling into the poverty trap is explained by initial depopulation, which depresses the scale effect on productivity growth. In addition to the main result, a permanent decline in parental altruism or in the fixed cost of child rearing raises the hurdle to sustainable growth and may thereby divert the economy from the pro- sperous path.
Without taking a unified-approach, the present paper focuses on the developed economy whose initial fertility rate is below replacement level. As such, the unsolved questions are how the initial conditions are determined and why they are different among advanced countries. In order to answer them, it is necessary to extend the model and consider the process of fertility decline from a longer-term perspective. This theme is left for future research.
Acknowledgements
The authors are grateful to Koichi Futagami, Ken Tabata, and the participants of the 8th Conference of Macroeconomics for Young Professionals (2014, Osaka), the 2014 Asian Meeting of the Econometric Society, and the 2014 Australia Meeting of the Econometric Society, for their useful comments and encouragement. This research benefited from a Grant-in-Aid for JSPS Fellows (26-3695).
References
- Kremer, M. (1993) Population Growth and Technological Change: One Million B.C. to 1990. Quarterly Journal of Economics, 108, 681-716. http://dx.doi.org/10.2307/2118405
- Romer, P.M. (1990) Endogenous Technological Change. Journal of Political Economy, 98, S71-S102. http://dx.doi.org/10.1086/261725
- Aghion, P. and Howitt, P. (1992) A Model of Growth through Creative Destruction. Econometrica, 60, 323-351. http://dx.doi.org/10.2307/2951599
- Jones, C.I. (1999) Growth: With or Without Scale Effects? American Economic Review: Papers and Proceedings, 89, 139-144. http://dx.doi.org/10.1257/aer.89.2.139
- Prettner, K. (2013) Population Aging and Endogenous Economic Growth. Journal of Population Economics, 26, 811- 834. http://dx.doi.org/10.1007/s00148-012-0441-9
- Department of Economic and Social Affairs, Population Division, United Nations (2013) World Population Prospects: The 2012 Revision, Volume I: Comprehensive Tables ST/ESA/SER.A/336. http://esa.un.org/wpp/Documentation/pdf/WPP2012_Volume-I_Comprehensive-Tables.pdf
- Dalgaard, C.J. and Kreiner, C.T. (2001) Is Declining Productivity Inevitable? Journal of Economic Growth, 6, 187-203. http://dx.doi.org/10.1023/A:1011343715594
- Strulik, H. (2005) The Role of Human Capital and Population Growth in R & D-Based Models of Economic Growth. Review of International Economics, 13, 129-145. http://dx.doi.org/10.1111/j.1467-9396.2005.00495.x
- Department of Economic and Social Affairs, Population Division, United Nations (2014) World Population Prospects: The 2012 Revision, Methodology of the United Nations Population Estimates and Projections. Working Paper No. ESA/P/WP.235. http://esa.un.org/wpp/Documentation/pdf/WPP2012_Methodology.pdf
- Strulik, H., Prettner, K. and Prskawetz, A. (2013) The Past and Future of Knowledge-Based Growth. Journal of Economic Growth, 18, 411-437. http://dx.doi.org/10.1007/s10887-013-9098-9
- Galor, O. and Weil, D.N. (2000) Population, Technology, and Growth: From Malthusian Stagnation to the Demographic Transition and Beyond. American Economic Review, 90, 806-828. http://dx.doi.org/10.1257/aer.90.4.806
- Jones, C.I. (1995) R & D-Based Models of Economic Growth. Journal of Political Economy, 103, 759-784. http://dx.doi.org/10.1086/262002
- Romer, P.M. (1986) Increasing Returns and Long-Run Growth. Journal of Political Economy, 94, 1002-1037. http://dx.doi.org/10.1086/261420
- Maddison, A. (2006) The World Economy, Volume 1: A Millennial Perspective. The OECD Development Centre, Paris (Originally Published in 2001). http://dx.doi.org/10.1787/9789264022621-en
- Haveman, R. and Wolfe, B. (1995) The Determinants of Children’s Attainments: Findings and Review of Methods. Jour- nal of Economic Literature, 33, 1829-1878.
- de la Croix, D. and Doepke, M. (2003) Inequality and Growth: Why Differential Fertility Matters. American Economic Review, 93, 1091-1113. http://dx.doi.org/10.1257/000282803769206214
Appendix
A. Proof of Proposition 1
The properties of





where











Under the second condition in Equation (13),


from Equation (A.1).
B. Local Analysis of the Poverty Trap
From Equations (9) and (10),
where



where

Thus, it follows that

Now one finds that

where the function




NOTES
*Corresponding author.
1Jones [4] categorizes major R&D-based growth models, including the pioneer works referred in the text, by the effectiveness of scale effects on the growth rate of per capita income. He also argues that scale effects on the level of per capita income are at work in all of those models.
2By utilizing the existing endogenous growth models, Prettner [5] investigates the effect of population aging on long-run growth performance. However, population aging is not accompanied by a population decline in his model. The model developed below makes no distinction between these two types of demographic changes.
3The rise in fertility is consistent with a forecast of the United Nations, which is made by a time series model based on national experience (United Nations [9] , p. 17). In “more developed” regions, including Europe, Northern America, Australia, New Zealand, and Japan, total fertility turns upward around the year 2000, approaching to replacement level (United Nations [6] , p. viii and p. 12). While Strulik et al. ([10] , p. 432) demonstrate fertility recovery by controlling a weight parameter for children in utility, in the model developed below, the future trend in fertility depends on the initial conditions.
4While this paper extends the growth theory developed by Galor and Weil [11] , it does not take their unified approach. The focus here is on the modern era in which advanced economies have already experienced a demographic transition. Thus, the poverty trap presented in this paper does not describe the Malthusian stagnation, which results from population expansion under resource constraints.
5The scale effect on the growth rate of technology becomes negligible in the long run provided that the skill-augmenting effect is bounded above (cf. Footnote 13). The dissipation of the scale effect is in line with Jones [12] , whose model is more empirically plausible in this aspect than previous R&D-based growth theories.
6Measuring the child rearing costs in labor, rather than in time, is one of the crucial deviations from the model of Galor and Weil [11] . Such an extension generates an income effect on fertility, which is the potential force of population recovery in developed stages.
7In what follows,



8Given the properties of




9Recall that Equation (7) is the condition for
10This specification is viewed as a discrete counterpart of Equation
(9) proposed by Jones [12] , in which R&D exhibits no externalities. Taking
into account the long time interval of the OLG economy, it would be plausible to
consider that




11As a result of calibration based on the G-7 data, Strulik et al. ([10] , pp. 421 and 429) impose a similar restriction to the second inequality in Equation (A1). Unlike in the present model, however, their restriction makes the transition to the prosperous path automatic regardless of the initial conditions.
12A linear approximation reveals that




13In the case of divergence, the growth rate of technology converges
to a certain level if





14Applying the implicit function theorem to Equation (7),



15Negative population growth with low technology appears to be inconsistent
with the historical experience of most economies, whose population has been expanding
(cf. Maddison [14] , p. 241). As mentioned in the introduction, however, the focus
here is on the contemporary period in which advanced economies begin aging, and
encompassing the demographic patterns over the past millennia is beyond the scope
of the present research. For this reason, the initial technology level



16Strulik et al. [10] preclude such a case by setting the productivity
parameter for education investment so large that

17Equation (18) yields
18In light of Haveman and Wolf ([15] , Table 1) and de la Croix and Doepke ([16] , p. 1099), we choose the US as a representative developed country and assume that parents initially spend 7.25% of their potential income on the fixed cost and 7.3% on child education.
19The total fertility rate reported in the reference is 1.67. Note that
























