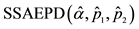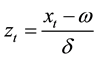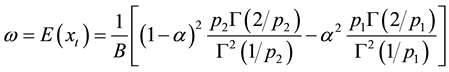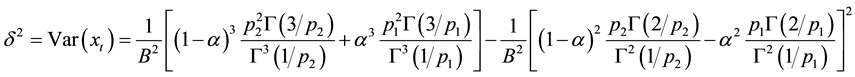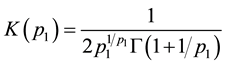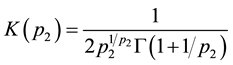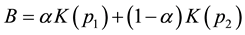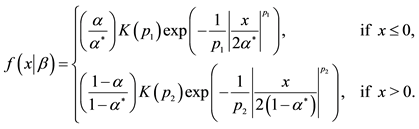Theoretical Economics Letters
Vol.04 No.09(2014), Article ID:51623,11 pages
10.4236/tel.2014.49095
Analysis of the Effect of Index Futures on Stock Market with a New Fama-French 3-Factor Model
Xinyue Bei1, Yanjia Yang2, Liuling Li3, Bruce Mizrach4
1Accounting Department, Bussiness School, Nankai University, Tianjin, China
2Finance Department, Economics School, Nankai University, Tianjin, China
3The Institute of Statistics and Econometrics, Economics School, Nankai University, Tianjin, China
4Rutgers University, Piscataway, USA
Email: xinyue_bei@126.com, yanjia_yang@yahoo.com, liliuling@nankai.edu.cn, mizrach@econ.rutgers.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 September 2014; revised 30 October 2014; accepted 17 November 2014
ABSTRACT
In this paper, the effect of Index Futures on stock market is studied. A new model, which is based on the 3-factor model in Fama and French (1993), the EGARCH-type volatility in Nelson (1991) and non-normal distribution of SSAEPD in Zhu and Zinde-Walsh (2009) is used. Fama-French 25 portfolios for US stock market (1951-2007) are analyzed. Following Pericli and Koutmos (1997), we divide data into 2 sub-samples: sample 1 (pre-SP500 Index Futures) and sample 2 (post-SP500 Index Futures). Our three main findings are as follows. Fama-French 3 factors are still alive in both samples. During the period of post-SP500 Index Futures, the coefficients in this new model become slightly lower and the volatility of stock market is bigger.
Keywords:
Index Futures, Fama-French 3-Factor Model, SSAEPD (Standardized Standard Asymmetric Exponential Power Distribution), EGARCH

1. Introduction
Trading of stock Index Futures was first introduced by the Kansas City Board of Trade on February 24, 1982. Then, the Chicago Mercantile Exchange began trading of SP500 Index Futures in April. After that, similar instruments were introduced in other countries, such as FTSE100 Index Futures in England, Composite Index Futures in Japan and All-Ordinaries Index Futures in Australia. The development of Index Futures has recieved many attensions.
One group of researchers show volatility of spot market is increased after the introduction of Index Futures. For example, Kang and Yoon (2007) found that the spot market became more volatile after the introduction of five Index Futures in Asia based on GARCH, GJR-GARCH and APGARCH model [1] . However, others show the opposite. Friedman, Harrison and Salmon (1983) suggested that spot prices tended to be less volatile after futures markets operate [2] . Gulen and Mayhew (2000) concluded stock Index Futures decreased the volatility of stock market in 25 countries (except US and Japan) [3] . Similar conclusion was drawn by Bologna and Cavallo (2002) [4] .
In addition to previous results, the 3rd groups of researchers show there is no statistically significance re- lationship between Index Futures and stock return. For example, Santoni (1987) analyzed SP500 index and found no significant change on stock index volatility [5] . Also, Xie and Huang (2014) use daily data of the China Securities Index (CSI) 300 between 2005 and 2012 and find that the launch of Index Futures does not decrease the volatility of the spot market [6] . Liu and Wang (2008) ran empirical test based on GARCH model and suggested that the introduction of Index Futures in Taiwan, Japan and South Korea did not increase the volatility in long term [7] . For other researches on Index Futures, one can refer to Table 1.
Following previous researches, this paper studies the influence of the Index Futures on stock market. SP500 Index Futures is analyzed. We use a new model based on the 3-factor model of Fama-French (1993), the EGARCH-type volatility of Nelson (1991) and non-Normal error of SSAEPD in Zhu and Zinde-Walsh (2009) [8] - [10] . This new model was first proposed by Yang (2013) [11] . The reason why we chose this new model was that it had better in-sample fit than that of Fama and French (1993).
In this paper, we will test following two hypotheses.
1) Are the 3 factors in Fama-French (1993) still alive if EGARCH-type volatility and non-Normal error are considered?
2) Can we find any differences before or after the introduction of SP500 Index Futures?
To answer these questions, Fama-French 25 portfolios are analyzed. Following Pericli and Koutmos (1997), we choose 1982 as the break point and divide the data into 2 sub-samples: pre-SP500 Index Futures as sample 1 (from September 1951 to March 1982) and post-SP500 Index Futures as sample 2 (from April 1982 to March 2007)1 [15] . Likelihood Ratio test (LR) is used for parameter restriction testings. Kolmogorov-Smirnov test (KS) is used for model diagnostics.
Empirical results show Fama-French 3 factors are alive in both samples. After the introduction of SP500 Index Futures, the estimates for Fama-French three factors becomes lower and show less fluctuating. And we find the coefficients in EGARCH equaltion becomes bigger so we conclude that the volatility of the stock market becomes higher.
This paper is organized as follows. Section 2 is the model and methodology. Section 3 is the empirical results. Section 4 is the conclusion.
2. Model and Methodology
2.1. FF-SSAEPD-EGARCH Model
In this paper, we apply following new model (denoted as FF-SSAEPD-EGARCH) to study the effect of Index Futures on stock returns2.
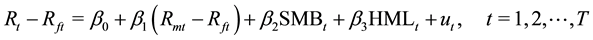 (1)
(1)
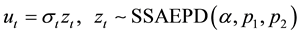
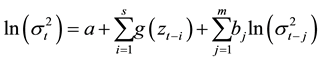
Table 1. Researches about the index futures and Fama-French 3-Factor model.
Note: “-” means information is not available in the paper. D means daily. M means monthly. Min means minite.
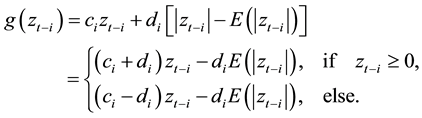 (2)
(2)
Here, 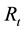 ,
, 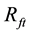 and
and 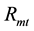 are the rate of return for stock portfolio, the risk-free rate and the return rate of the market at time
are the rate of return for stock portfolio, the risk-free rate and the return rate of the market at time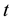 , respectively.
, respectively. 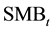 stands for small size (market capitalization) minus big size (market capitalization) and
stands for small size (market capitalization) minus big size (market capitalization) and 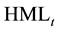 for high book-to-market ratio minus low book-to-market ratio. The conditional
for high book-to-market ratio minus low book-to-market ratio. The conditional
standard deviation is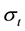 , i.e., volatility.
, i.e., volatility. 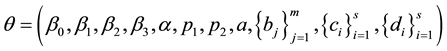 are the para-
are the para-
meters to be estimated. The error term 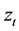 is distributed as the Standardized Standard Asymmetric Exponential Power Distribution (SSAEPD) proposed by Zhu and Zinde-Walsh (2009). The probability density function (PDF) of
is distributed as the Standardized Standard Asymmetric Exponential Power Distribution (SSAEPD) proposed by Zhu and Zinde-Walsh (2009). The probability density function (PDF) of 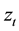 is
is
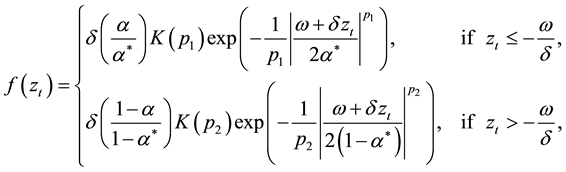 (3)
(3)


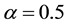
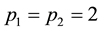
2.2. Method of Maximum Likelihood Estimation
The maximum likelihood function for this new model is
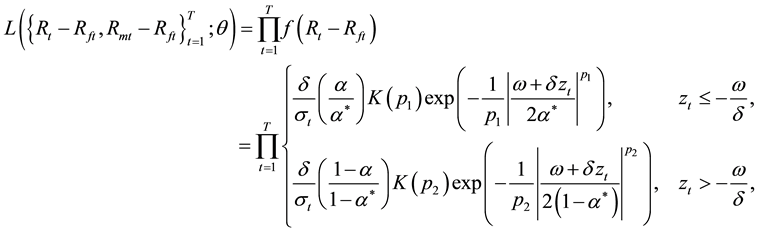
where

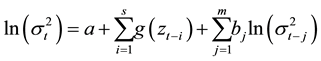
3. Empirical Analysis
3.1. Data
In this paper, we study the effect of SP500 Index Futures on stock returns. The data used are the monthly return for the Fama-French 25 portfolios, which is downloaded from the French’s Data Library4. The sample period is from September 1951 to March 2007 with 666 observations. Following Pericli and Koutmos (1997), we select April 1982 as the breakpoint and set pre-SP500 Index Futures as sample 1 (from September 1951 to March 1982, the period before the introduction of SP500 Stock Index Futures) and the post-SP500 Index Futures as sample 2 (from April 1982 to March 2007, the period after the introduction of SP500 Stock Index Futures).
The descriptive statistics of these samples are listed in Table 2. The P-value of Jarque-Bera test for most portfolios is smaller than 5% significance level5. Hence, we conclude the asset returns in both samples do not follow Normal distribution.
3.2. Empirical Results
3.2.1. Estimations
For sample 1, the estimations are listed in Table 3. According to the results, all estimates of 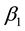
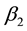
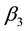
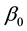
For the parameters in SSAEPD, the estimates of 
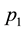
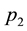
In the EGARCH model, most estimates of a are close to zero and 14 estimates in sample 1 (5 estimates in sample 2) are statistically significant. 24/25 estimates of b in sample 1 (all in sample 2) are statistically sig- nificant. 18 estimates of c in sample 1 (22 estimates in sample 2) are not statistically significant, so we conclude that the good news and bad news do not have significant different impact on volatility. 11 estimates of d in sample 1 (22 estimates in sample 2) are statistically significant. Hence, we conclude that the asymmetric effect is not documented in the data.
3.2.2. Comparisions
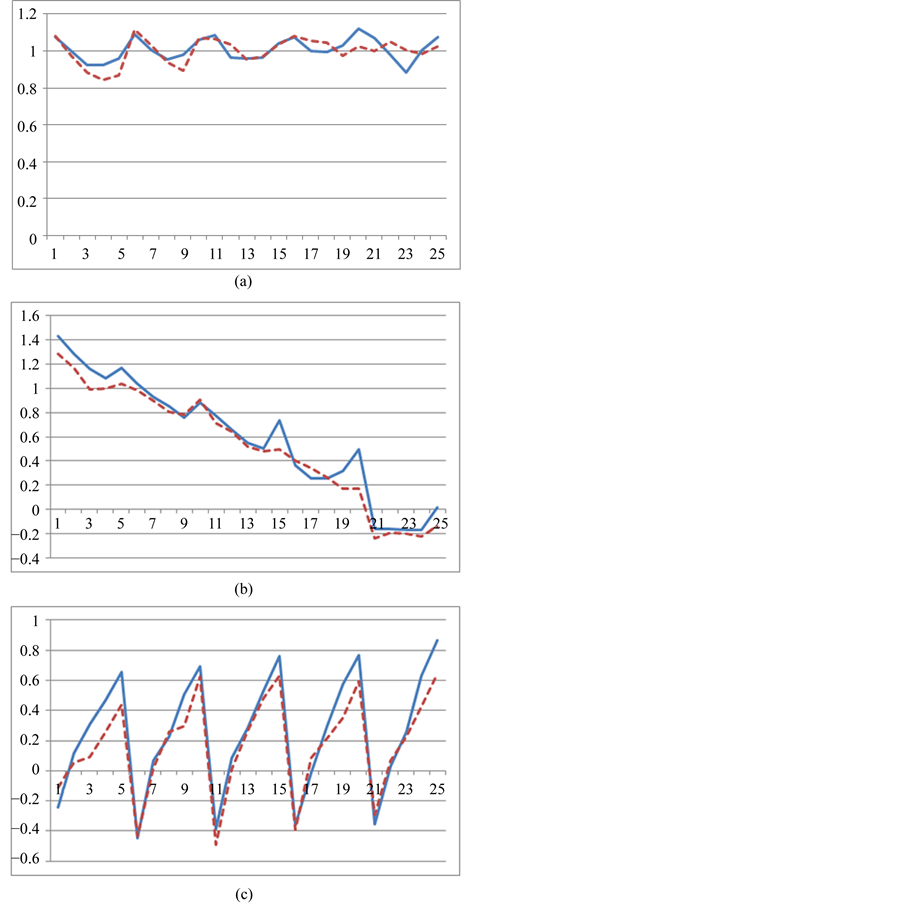
To compare the factors before and after the introduction of SP500 index futures, we plot the estimates of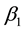

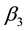


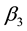
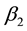
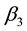
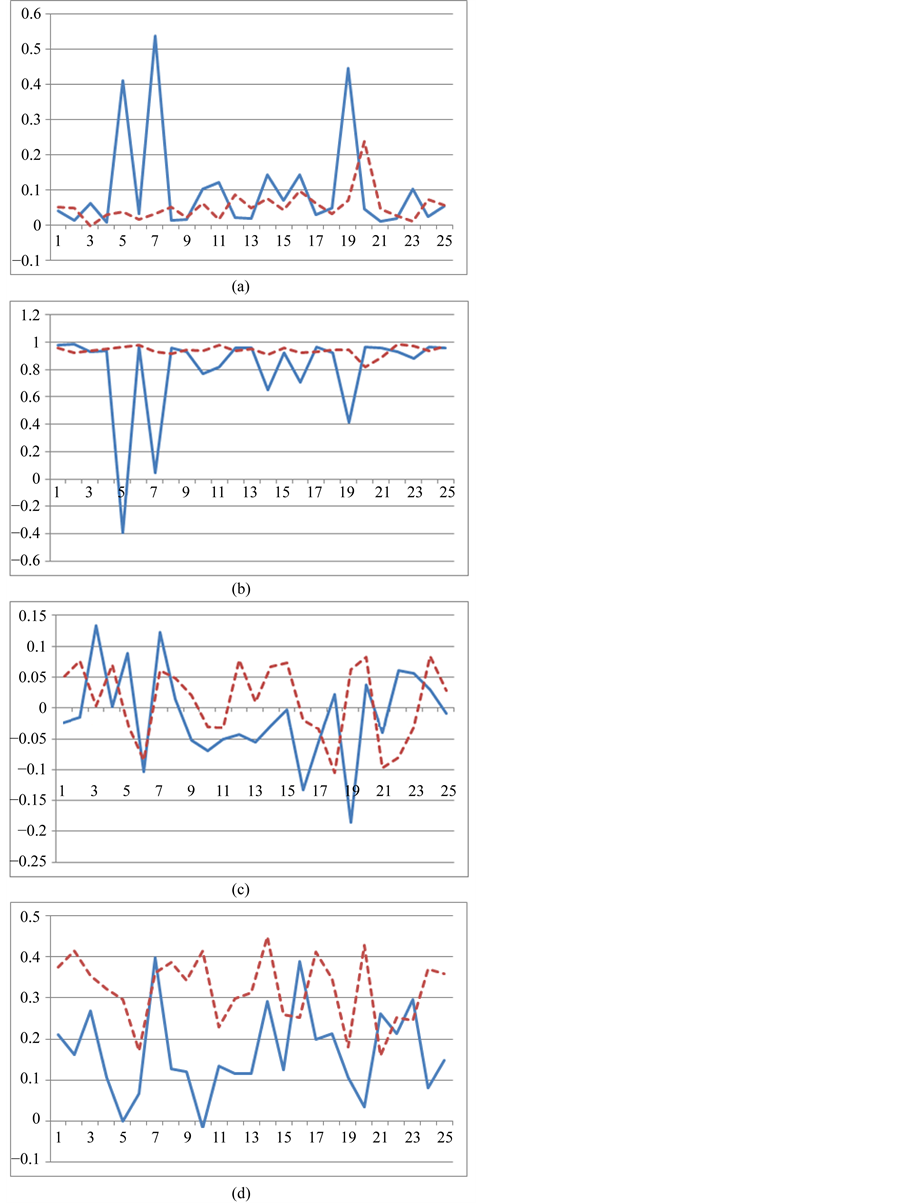
To compare the volatility of stock market, we plot the estimates of a, b, c, d in the EGARCH equation (see Figure 2). As mentioned above, most of the a and c values are small and close to zero so the values of condition
Table 2. Descriptive statistics.
Table 3. Estimates from sample 1 (pre-SP500 index futures).
Notes: *means the data reject the null hypothesis under 5% significance level. H0:β0 = 0, H0:β1 = 0, H0:β2 = 0, H0:β3 = 0, H0:α = 0.5, H0:p1 = 2, H0:p2 = 2, H0:a = 0, H0:b = 0, H0:c = 0, H0:b = 0.
Table 4. Estimates from sample 2 (post-SP500 index futures).
Notes: *means the data reject the null hypothesis under 5% significance level. H0:β0 = 0, H0:β1 = 0, H0:β2 = 0, H0:β3 = 0, H0:α = 0.5, H0:p1 = 2, H0:p2 = 2, H0:a = 0, H0:b = 0, H0:c = 0, H0:b = 0.
Figure 1. Comparisons of slope coefficient estimates in the mean equation during Pre- and Post-SP500 index futures (Y-axis is the value of βi (i = 1, 2, or 3). X-axis is the Fama-French 25 Portfolios. Solid line represents Pre-SP500 index futures and dotted line represents Post-SP500 index futures). (a) β1 values; (b) β2 values; (c) β3 values.
standard deviation depends mostly on the values of c, b and d. We discover that the estimates of both b and d are bigger in sample 2. So we conclude that the volatility becomes higher after the introduction of index futures.
3.3. Model Diagnostics (Residual Check)
In this section, we implement Kolmogorov-Smirnov test to check residuals for FF-SSAEPD-EGARCH model. Our results show the residuals of all the 25 portfolios from the model do follow SSAEPD, which means that the model is adequate for the Fama-French 25 portfolios.
The P-values of KS tests7 are displayed in Table 5. For example, the P-value of the portfolio with Smal Size
Figure 2. Comparisons of estimates in the GARCH equation during Pre- and Post- SP500 Index Futures (Y-axis is the value of a, b, c or d. X-axis is the Fama-French 25 portfolios. Solid line represents Pre-SP500 index futures and dotted line re- presents Post-SP500 index futures). (a) a values; (b) b values; (c) c values; (d) d values.
Table 5. P-values of KS test for residuals.
and Low Book-to-market in sample 1 is 0.77, greater than 5%. That means, under 5% significance level, the null hypothesis is not rejected and the residuals from the FF-SSAEPD-EGARCH model do follow the SSAEPD. Similar results are documented for all portfolios in two samples. Hence, we conclude the errors of the model do follow SSAEPD. i.e., the FF-SSAEPD-EGARCH model is adequate for most Fama-French 25 portfolios.
4. Conclusions and Future Extensions
In this paper, we study the effect of SP500 Index Futures on stock returns with a new model. This new model considers the EGARCH-type volatility in Nelson (1991), non-normal error of SSAEPD in Zhu and Zinde- Walsh (2009), and the 3-factor model of Fama and French (1993). Data of Fama-French 25 portfolios are used. We divide data into 2 samples: sample 1 (pre-SP500 Index Futures, from September 1951 to March 1982), sample 2 (post-SP500 Index Futures, from April 1982 to March 2007). Method of Maximum Likelihood Estimation is used to estimate this model and Likelihood Ratio test (LR) is used to test parameter restrictions.
Empirical results show Fama-French three factors are alive in both samples. After the introduction of SP500 Index Futures, the estimates for Fama-French three factors become lower and show less fluctuating and the volatility of the stock market becomes higher.
Future extensions will include but not limited to follows. First, different data can be used to study the influence of index futures. Second, different methods such as dummy variables could be used. Last but not least, subsample periods can be changed to check the robustness of our results.
Acknowledgements
The authors wish to thank participants in the seminars organized by Economics School at Nankai University, China and Economics School at Rutgers University, USA. We also want to thank participants in the conference organized by Risk Management Institute, National University of Singapore (July 16-17, 2010), the Singapore Economic Review Conference (August 4-6, 2011), the International Conference on Applied Business & Economics at Manhattan, NY, USA (Oct. 2-4, 2013), the 8th International Conference on Asian Financial Markets & Economic Development at Nagasaki University (Dec. 7-8, 2013), Japan, the World Finance & Banking Symposium at Beijing, China (Dec. 16-17, 2013), the 2014 China Finance Review International Conference at Shanghai, China (July 26-27, 2014), and BIT’s 1st Annual Global Congress of Knowledge Economy at Qsingdao, China (Sept. 21-23, 2014). The authors are responsible for all errors.
Cite this paper
XinyueBei,YanjiaYang,LiulingLi,BruceMizrach, (2014) Analysis of the Effect of Index Futures on Stock Market with a New Fama-French 3-Factor Model. Theoretical Economics Letters,04,748-759. doi: 10.4236/tel.2014.49095
References
- 1. Kang, S.H. and Yoon, S.-M. (2007) Index Futures Trading and Asymmetric Volatility: Evidence from Asian Stock Markets. The Journal of the Korean Economy, 8, 273-293.
http://www.econbiz.de/Record/index-futures-trading-and-asymmetric-volatility-evidence-from-asian-stock-markets-kang-sang-hoon/10009772044 - 2. Friedman, D., Harrison, G.W. and Salmon, J.W. (1983) The Informational Role of Futures Markets and Learning Behavior: Some Experimental Evidence. In: Streit, M.E., Ed., Futures Markets—Modelling, Managing and Monitoring Futures Trading, Basil Blackwell, Oxford.
http://www.econbiz.de/Record/the-informational-role-of-futures-markets-and-learning-behaviour-some-experimental-evidence-friedman-daniel/10003528165 - 3. Gulen, H. and Mayhew, S. (2000) Stock Index Futures Trading and Volatility in International Equity Markets.
The Journal of Futures Markets, 20, 661-685.
http://dx.doi.org/10.1002/1096-9934(200008)20:7<661::AID-FUT3>3.0.CO;2-R - 4. Bologna, P. and Cavallo, L. (2002) Does the Introduction of Stock Index Futures Effectively Reduce Stock Market Volatility? Is the “Futures Effect” Immediate? Evidence from the Italian Stock Exchange Using GARCH. Applied Financial Economics, 12, 183-192. http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2023037 http://dx.doi.org/10.1080/09603100110088085
- 5. Santoni, G.J. (1987) Has Programmed mTrading Made Stock Price More Volatile. Federal Reserve Bank of St. Louise Review, 18-29. http://www.econbiz.de/Record/has-programmed-trading-made-stock-prices-more-volatile-santoni-gary-james/10001027292
- 6. Xie, S.Q. and Huang, J.J. (2014) The Impact of Index Futures on Spot Market Volatility in China. Emerging Markets Finance & Trade, 50, 167-177.
http://econ.pku.edu.cn/upload/file/20140318/20140318161780068006.pdf http://dx.doi.org/10.2753/REE1540-496X5001S111 - 7. Liu, F.G. and Wang, X.F. (2008) The Empricial Analyse on the Relationship of Index Future and Stock Market Volatility. Finance and Trade Research, 3, 86-94.
http://www.cnki.net/KCMS/detail/detail.aspx?QueryID=37&CurRec=4&dbcode=CJFQ&dbname=CJFD 2008&filename=CMYJ200803019&urlid=&yx=&uid=WEEvREcwSlJHSldTTGJhYkdRUjJaMEdqYTBuNWtIQ VUveEVxREd5ZFVUdndkMG13aHhrSDM1aldSeWdWeG8ycTM0VT0=$9A4hF_YAuvQ5obgVAqNKPCYcEj KensW4IQMovwHtwkF4VYPoHbKxJw!!&v=MjY5NjIxTHV4WVM3RGgxVDNxVHJXTTFGckNVUkw2ZVorUm 5GeW5nVUw3SkppRFNaTEc0SHRuTXJJOUViWVI4ZVg - 8. Fama, E.F. and French, K.R. (1993) Common Risk Factors in the Returns on Stocks and Bonds. Journal of Nancial Economics, 33, 3-56. http://www.defaultrisk.com/pa_related_01.htm
- 9. Nelson, D.B. (1991) Conditional Heteroskedasticity in Asset Returns: A New Approach. Econometrica. Journal of the Econometric Society, 59, 347-370.
https://ideas.repec.org/a/ecm/emetrp/v59y1991i2p347-70.html
http://dx.doi.org/10.2307/2938260 - 10. Zhu, D. and Zinde-Walsh, V. (2009) Properties and Estimation of Asymmetric Exponential Power Distribution. Journal of Econometrics, 148, 86-99.
http://www.sciencedirect.com/science/article/pii/S0304407608001668 http://dx.doi.org/10.1016/j.jeconom.2008.09.038 - 11. Yang, Y. (2013) A New Fama-French 3-Factor Model with EGARCH-Type Volatilities and SSAEPD Errors. Working Paper, Finance Department, Economics School, Nankai University, Tianjin.
- 12. Rahman, S. (2001) The Introduction of Derivatives on the Dow Jones Industrial Average and Their Impact on the Volatility of Component Stocks. Journal of Futures
Markets, 21, 633-653.
http://www.researchgate.net/publication/229881535_The_Introduction_of_Derivatives_on_the_Dow_Jones_Industrial_Average_and_Their_Impact_on_the_Volatility_of_Component_Stocks
http://dx.doi.org/10.1002/fut.1702 - 13. Lien, D. and Yang, L. (2008) Asymmetric Effect of Basis on Dynamic Futures Hedging: Empirical Evidence from Commodity Markets. Journal of Banking & Finance, 32, 187-198.
https://ideas.repec.org/a/eee/jbfina/v32y2008i2p187-198.html http://dx.doi.org/10.1016/j.jbankfin.2007.01.026 - 14. Hwang, S. and Satchell, S.E. (2000) Market Risk and the Concept of Fundamental Volatility: Measuring Volatility across Asset and Derivative Markets and Testing for the Impact of Derivatives Markets on Financial Markets. Journal of Banking & Finance, 24, 759-785.
https://ideas.repec.org/a/eee/jbfina/v24y2000i5p759-785.html - 15. Pericli, A.
and Koutmo, G. (1997) Index Futures and Options and Stock Market Volatility.
Journal of Futures Markets, 17, 957-974.
http://dx.doi.org/10.1002/(SICI)1096-9934(199712)17:8<957::AID-FUT6>3.0.CO;2-K - 16. Zhong, M.S., Darrat, A.F. and Otero, R. (2003) Price Discovery and Volatility Spillovers in Index Futures Markets: Some Evidence from Mexico. Journal of Banking & Finance, 28, 3037-3054. http://www.sciencedirect.com/science/article/pii/S0378426604000305
- 17. Rita, M.A. (2003) Maturity Effects in Futures Markets: Evidence from Eleven Financial Futures Markets. Working Paper, Santa Cruz Center for International Economics.
http://escholarship.org/uc/item/1n04g31b - 18. Matanovic, E. and Wagner, H. (2012) Volatility Impact of Stock Index Futures Trading: A Revised Analysis.
Journal of Applied Finance & Banking, 2, 113-126.
https://ideas.repec.org/p/pra/mprapa/51204.html - 19. Alexakis, P. (2007) On the Effect of Index Futures Trading on Stock Market Volatility. International Research Journal of Finance and Economics, 11.
http://wenku.baidu.com/view/266fe3ef0975f46527d3e1fb.html - 20. Basdas, ü. (2009) Lead-Lag Relationship between the Spot Index and Futures Price for the Turkish Derivatives Exchange. Working Paper. http://papers.ssrn.com/sol3/papers.cfm?abstract_id=1493147
- 21. Xie, H. and Li, J. (2010) Intraday Volatility Analysis on S&P 500 Stock Index Future. International Journal of Economics and Finance, 2. http://ccsenet.org/journal/index.php/ijef/article/view/5894
- 22. Carhart, M.M. (1997) On Persistence in Mutual Fund Performance. The Journal of Finance, 52, 57-82. http://onlinelibrary.wiley.com/doi/10.1111/j.1540-6261.1997.tb03808.x/abstract
- 23. Gharghori, P., Mudumba, S. and Veeraraghavan, M. (2007) How Smart Is Money? An Investigation into Investor Behaviour in the Australian Managed Fund Industry. Pacific-Basin Finance Journal, 15, 494-513. http://dx.doi.org/10.1016/j.pacfin.2006.10.002
- 24. He, Y. (2008) An Improvement of Fama French Three-Factor Model Based on State Switch Information. Chinese Journal of Management Science, 16, 7-15. (In Chinese)
http://www.zgglkx.com/CN/abstract/abstract12793.shtml - 25. Wang, H. (2012) Aceruals Quality and Asset Pricing—Evidence from Chinese Stock Markets. Working Paper. http://www.cnki.net/KCMS/detail/detail.aspx?QueryID=63&CurRec=2&recid=&filename =1011233281.nh&dbname=CDFDLAST2012&dbcode=CDFD&pr=&urlid=&yx=&uid=WEEvREcwSlJHSld TTGJhYlN6MzFCNXBBK2NjdXdYMkpIQ1h6Mis0dUw3UW1XZmd6dHlqMHp2NnZ1aEc1Vmg2Q3RNZz0=$9 A4hF_YAuvQ5obgVAqNKPCYcEjKensW4IQMovwHtwkF4VYPoHbKxJw!!&v=MzI3NTdML0lWRjI2SDdHN 0hkUEVycEViUElSOGVYMUx1eFlTN0RoMVQzcVRyV00xRnJDVVJMNmVaK1JvRkN2blY
NOTES
1We choose short sample periods because we think shorter period may reduce the noise such as the impact of other unrelated events on stock market. Also, we set the end of sample period before April 2007 because during the period of 2007 financial crisis, the volatility is too big, which is not related to oil crisis.
2Based on the 3-factor model in Fama and French (1993), the EGARCH-type volatility in Nelson (1991) and non-Normal error of SSAEPD in Zhu and Zinde-Walsh (2009), a new 3-factor model is proposed by Yang (2013). Yang (2013) denotes this new model as the FF- SSAEPD-EGARCH model, whose MatLab program is revised from that of Yin (2011). And in this paper, we first exam the simulation program of Yang (2013) and then apply this model and methodology to analyze data.
3By changing variable techniques, we obtain PDF of
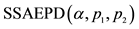
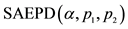
4Thanks Yin (2011) who provides the well organized Excel files. Thanks Professor French for kindly providing the risk free rate by e-mail.
5Only the P-value of JB test of the (5,2) portfolio in sample 1 is more than 0.05.
6
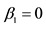
7The null hypothesis of KS test is H0: FF-SSAEPD-EGARCH residuals
are distributed as