Theoretical Economics Letters
Vol.04 No.08(2014), Article ID:50305,4 pages
10.4236/tel.2014.48080
Asset Prices, Nominal Rigidities, and Monetary Policy: Negative Monetary Policy Responses to Asset Price Fluctuations
Kengo Nutahara1,2
1Department of Economics, Senshu University, Kanagawa, Japan
2The Canon Institute for Global Studies, Tokyo, Japan
Email: nutti@isc.senshu-u.ac.jp
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 July 2014; revised 24 August 2014; accepted 20 September 2014
ABSTRACT
Carlstrom and Fuerst [“Asset Prices, Nominal Rigidities, and Monetary Policy,” Review of Economic Dynamics, Vol. 10, 2007, pp. 256-275] find that a positive monetary policy response to share prices is a source of equilibrium indeterminacy. In this note, we investigate the negative response of a central bank to share prices. We find that a negative monetary policy response to share prices is also a source of equilibrium indeterminacy.
Keywords:
asset prices, monetary policy, equilibrium determinacy

1. Introduction
Should monetary policy respond to asset price fluctuations? To this classic monetary policy question, a recent paper by Carlstrom and Fuerst [1] provides a negative answer. They find that equilibrium indeterminacy arises if monetary policy positively responds to share prices in a standard sticky-price economy. An increase in inflation reduces firm’s profits, and share prices decline since they reflect the firm’s profits. Then, the monetary policy response to share prices implicitly weakens the overall reactions to inflation. This is a source of equilibrium indeterminacy in their model.
The intuition of Carlstrom and Fuerst’s [1] to this indeterminacy result would lead one to think that negative monetary responses might be good from the viewpoint of equilibrium determinacy. The work by Faia and Monacelli [2] is closely related to this conjecture. They find that the optimal monetary policy is to respond to asset prices negatively in a sticky price model with financial frictions a la Carlstrom and Fuerst [3] .
To address this question, we extend the model of [1] where a central bank can respond to asset prices negatively. We find that equilibrium indeterminacy also arises by a negative monetary response to asset prices. If a central bank responds to asset prices negatively, an increase in asset prices lowers the nominal interest rate. Since the asset price is the discounted sum of firms’ profits, this decrease in the nominal interest rate means a decrease in the discount rate. Then, there is an upward pressure of asset prices, and an increase in the asset price causes further increases in the asset price. This is a source of equilibrium indeterminacy from a negative monetary response to asset prices.
The rest of this paper is organized as follows. Section 2 introduces our model. Section 3 presents the main results and their interpretation. Section 4 discusses the robustness of the results. Finally, Section 5 presents our concluding remarks.
2. The Model
Our model is the same as that of [1] . Nominal prices are sticky and there is no capital, assets are shares of monopolistic competitive firms, and the asset price is defined as the discounted sum of monopolistic competitive firms’ profits.
The linearized equilibrium system is given as follows:
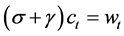 , (1)
, (1)
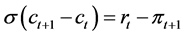 , (2)
, (2)
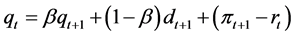 , (3)
, (3)
 (4)
(4)
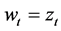 (5)
(5)
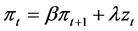 (6)
(6)
 (7)
(7)
where 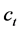 denotes consumption;
denotes consumption;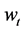 , the real wage rate;
, the real wage rate;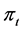 , the inflation rate;
, the inflation rate;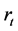 , the nominal interest rate;
, the nominal interest rate;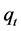 , share prices;
, share prices; , the dividend; and
, the dividend; and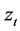 , the real marginal cost.
, the real marginal cost. 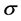 denotes the relative risk aversion;
denotes the relative risk aversion;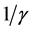 , the Frisch elasticity;
, the Frisch elasticity;



As shown by [1] , the dividend is given by

where

We employ an assumption on 
Assumption 1.
Under this assumption, an increase in the real marginal cost decreases the dividend.
The equilibrium system is reduced to the following matrix form:
where

The first equation is the consumption Euler equation (2); the second, the New Keynesian Phillips curve (6); and the third, the Euler equation for share (3).
For the analysis, we transform this system as follows:
where
3. Main Results
A necessary and sufficient condition for the equilibrium determinacy of this three-dimensional system is as follows
Proposition 1. Suppose that

where
Proof. A necessary and sufficient condition for equilibrium determinacy is that all roots of 

where
Necessary and sufficient conditions for equilibrium determinacy are







Q.E.D.
Since
Corollary 1. Suppose that 


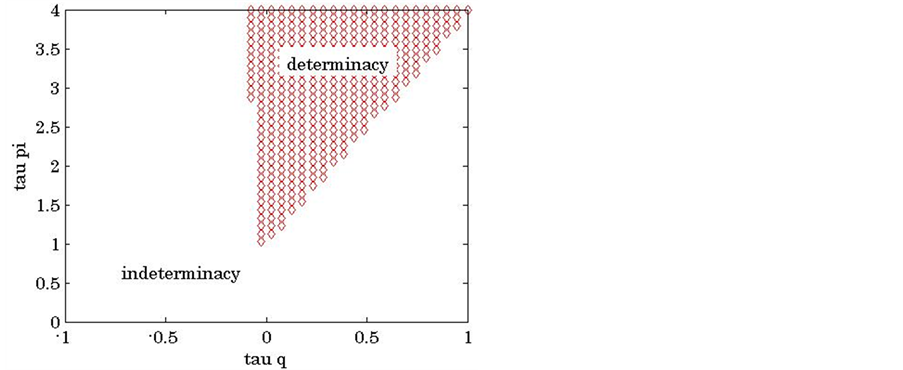
Figure 1 shows the determinacy and indeterminacy regions by numerical simulations. The vertical axis is the
Figure 1. Determinacy regions (1): Baseline.
central bank’s stance on inflation






The existence of the upper bound of 

Why is there a lower bound,
4. Robustness: Sticky Price-Wage Economy
In the case where wages are also sticky a la [4] , the linearized intratemporal optimization condition (1) becomes

and the following two equations are introduced to the log-linearized equilibrium system:


where 
In this case, it is difficult to derive an analytical condition for equilibrium determinacy. Then, we calculate the determinacy region by numerical simulations. Figure 2 is the analogue of Figure 1. We set 
5. Concluding Remarks
In this paper, the effects of monetary policy responses to asset prices are investigated. [1] found that a positive monetary policy response is a source of equilibrium indeterminacy since it implies that the monetary policy response to share price implicitly weakens the overall reaction to inflation. Following this intuition, negative monetary policy response to asset prices might be good for equilibrium determinacy because it might strengthen the
Figure 2. Determinacy regions (2): Sticky price-wage economy.
all overreaction to inflation. We have found that negative monetary policy response is also a source of indeterminacy. This is because an increase in asset prices generates further increases in asset prices through monetary policy. Therefore, the central bank should not respond to asset prices both positively and negatively from the viewpoint of equilibrium indeterminacy.
Acknowledgements
I would like to thank Keiichiro Kobayashi for their helpful comments and suggestions. Of course, the remaining errors are mine. This work was funded by a Senshu University research grant (“Equilibrium Indeterminacy, Share Prices, and Monetary Policy”) in 2012.
References
- Carlstrom, C.T. and Fuerst, T.S. (2007) Asset Prices, Nominal Rigidities, and Monetary Policy. Review of Economics Dynamics, 10, 256-275. http://dx.doi.org/10.1016/j.red.2006.11.005
- Faia, E. and Monacelli, T. (2007) Optimal Interest Rate Rules, Asset Prices, and Credit Frictions. Journal of Economics Dynamics and Control, 31, 3228-3254. http://dx.doi.org/10.1016/j.jedc.2006.11.006
- Carlstrom, C.T. and Fuerst, T.S. (1997) Agency Costs, Net Worth, and Business Fluctuations: A Computable General Equilibrium Analysis. American Economic Review, 87, 893-910. http://www.jstor.org/stable/2951331
- Erceg, C.J., Henderson, D.W. and Levin, A.T. (2000) Optimal Monetary Policy with Staggered Wage and Price Contracts. Journal of Monetary Economics, 46, 281-313. http://dx.doi.org/10.1016/S0304-3932(00)00028-3