Theoretical Economics Letters
Vol.4 No.3(2014), Article ID:44545,7 pages DOI:10.4236/tel.2014.43026
Efficacy in Education and Intergenerational Wellbeing
Masayuki Otaki
Institute of Social Sciences, University of Tokyo, Tokyo, Japan
Email: ohtaki@iss.u-tokyo.ac.jp
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 19 February 2014; revised 19 March 2014; accepted 26 March 2014
ABSTRACT
We consider an intergenerational and educational investment stochastic model to determine the effects of efficacy in education on affluence over time. Efficacy in education, defined by the success probability of intergenerational education, seriously affects the affluence in the long run of families concerned with the prosperity of descendants. This is because since lenders of educational investment funds cannot take collateral for humanitarian reasons, families without sufficient wealth are excluded from educational opportunities. If education is more effective, the accumulation of wealth releases more households from the threat of bankruptcy in the future.
Keywords:Eficacy in Education, Intergenerational Wellbeing, Lexicographic Utility, Social Stratification, Pedagogical Skills, Random Walk with One-Sided Absorbing Barrier

1. Introduction
When parents are deeply devoted to their descendants’ wellbeing, they strive to save as much money as possible. This is because their descendants might not be able to sustain investment in education when their wealth is constrained and borrowing from outside of the family is difficult.
This stems from the fact that educational investment is financed without collateral for humanitarian reasons and that the effort that would be expensed by beneficiary towards ensuring success in education is not verifiable. Financial intermediaries estimate rationally that a wealthy and deeply committed family achieves high performance in education because it loses more income when its education fails. Such properties of educational investment are analyzed by Otaki [1] based on Arrow [2] and Stiglitz and Weiss [3] .
This article analyzes how efficacy in education, which is defined by the “success” probability of a child in education, affects wealth accumulation. “Success” means that educated children acquire good natured and socialized characteristics and become able to earn reasonable incomes, according to Dewy [4] who considers such success the ultimate aim of education1. It does not mean the acquisition of abilities for uncommonly high incomes.
When education efficacy is sufficiently high, as wealth accumulation advances, most families are released from the fear of bankruptcy (i.e. constrained educational funds). On the other hand, in the case of low efficacy, the accumulation of wealth is hindered, even though parents have a lexicographic preference for their descendants’ wellbeing over their own.
This is because over time, success is canceled by low efficacy in education and, thus, it does not improve the sustainability of the family in being able to obtain educational funding. Consequently, if efficacy is low, the fruits of education are dissipated rather than being reinvested.
Efficacy depends not only on the contributions of a family’s own funds but also on skills deployed by teachers since education comprises mutual communication. In other words, when each family can finance educational costs from its own wealth, the decisive factor that enables the sustenance of intergenerational affluence, is scholastic skills. Nevertheless, educational economics has not given much importance to such skills2.
The rest of the paper is organized as follows. Section 2 constructs an intergenerational and educational investment stochastic model under asymmetric information. In Section 3, we analyze the dynamic aspects of the model. Section 4 provides brief concluding remarks.
2. The Model
2.1. The Back Ground of the Model
It is a well-known statistical property that there is a robust positive correlation between enrollment rates and real GDP per capital. For example, Mankiw, Romer and Weil [6] reveal that human capital accumulation significantly stimulates economic growth by using cross country data.
However, converse causality is also thinkable and emphasized mostly by researchers who are engaged in development economics. That is, lower income hinders educational opportunities. Ito [7] reports, taking the seriousness of child labor into consideration, that there is also quite a significant positive relationship between PPP adjusted GDP per capita and secondary enrollment rate.
We consider that such causalities coexist, and hence, we construct a model which enables to analyze both causalities simultaneously.
2.2. The Structure of the Model and Its Analysis
We regard an extended family as a kind of dynasty. Each individual has the following lexicographic utility. He or she gives maximum priority to the sustainability of the family, and thereafter regards his private wellbeing. An extended family is assumed to be sustained as long as its constituents can continue to be educated and earn decent incomes to purchase various perishable goods. In other words, accumulated non-perishable assets within the extended family serve as the capital from which to produce perishable goods.
Furthermore, if parents succeed in educational investment, they obtain 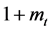 units of non-perishable goods (or consumable), and obtain nothing when they fail.
units of non-perishable goods (or consumable), and obtain nothing when they fail.  is the amount of non-perishable goods that the family must outlay for educational investment during period
is the amount of non-perishable goods that the family must outlay for educational investment during period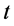 .
.
Thus, the net return during period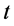 ,
,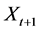 is
is
 . (1)
. (1)
The sum of accumulated non-perishable goods at the beginning of period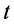 ,
, 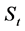 is
is
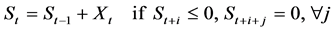 . (2)
. (2)
That is, 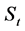 follows a random walk process with one-sided absorbing barrier
follows a random walk process with one-sided absorbing barrier . This implies that a family cannot recover from an uncultivated (uneducated and with very low income)situation once it is bankrupt, because a financial intermediary cannot lend money to a non-wealthy family as will be proved below.
. This implies that a family cannot recover from an uncultivated (uneducated and with very low income)situation once it is bankrupt, because a financial intermediary cannot lend money to a non-wealthy family as will be proved below.
Parents and their children cooperatively strive to succeed in educational investment. The more they strive, the higher the success probability becomes. Let us denote the relationship between efforts, ![]() , measured in terms of non-perishable goods and success probability,
, measured in terms of non-perishable goods and success probability, ![]() as
as
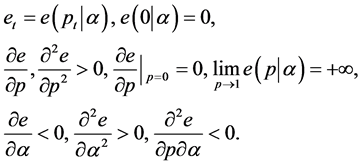 (3)
(3)
where ![]() denotes pedagogical skills deployed by a teacher that strengthen efficacy in education.
denotes pedagogical skills deployed by a teacher that strengthen efficacy in education.
Afamily that does not have sufficient educational funds possibly enters into a debt contract with a financial intermediary. Then, the instantaneous payoff of a family,  becomes
becomes
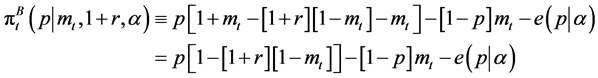 , (4)
, (4)
where 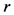 is the borrowing interest rate from the financial intermediary. It is clear from Equation (4) that a non-wealthy family, whose wealth,
is the borrowing interest rate from the financial intermediary. It is clear from Equation (4) that a non-wealthy family, whose wealth, 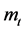 is located in the vicinity of 0, does not apply for the educational loan, because the return becomes negative. That is,
is located in the vicinity of 0, does not apply for the educational loan, because the return becomes negative. That is,
Lemma 1.
Some lump-sum of wealth is necessary for accessing educational investment. In turn, non-wealthy families are excluded from educational investment and are forced to dissipate their own income.
A family maximizes 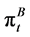 with respect to
with respect to![]() . Assuming an interior solution, we obtain the following firstorder condition.
. Assuming an interior solution, we obtain the following firstorder condition.
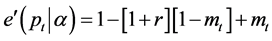 . (5)
. (5)
Furthermore, we assume that there exits 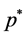 such as
such as
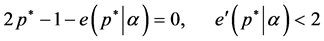 . (6)
. (6)
Equation (6) guarantees that the optimal success probability is larger than 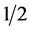 around the vicinity of
around the vicinity of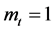 . This condition also implies that the expected return without borrowing,
. This condition also implies that the expected return without borrowing, 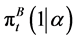 satisfies
satisfies
 . (7)
. (7)
Equation (5) is illustrated in Figure 1. It is apparent that 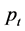 is a monotonously increasing function of
is a monotonously increasing function of 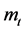 and a decreasing function of
and a decreasing function of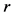 . Let us denote this relationship as
. Let us denote this relationship as
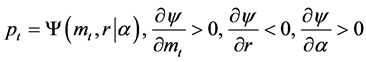 . (8)
. (8)
Equation (8) implies that a family, which can afford to provide sufficient funds for education, strives to succeed more because it has lost more wealth than a less wealthy family.
In addition, we assume that the loan market is competitive, and thus the profits of a financial intermediary are equal to zero. When the deposit rate is zero, the zero-profit condition of a financial intermediary is
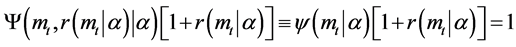 . (9)
. (9)
Equation (8) defines implicitly the equilibrium loan rate,  , which is applied to a family whose own
, which is applied to a family whose own
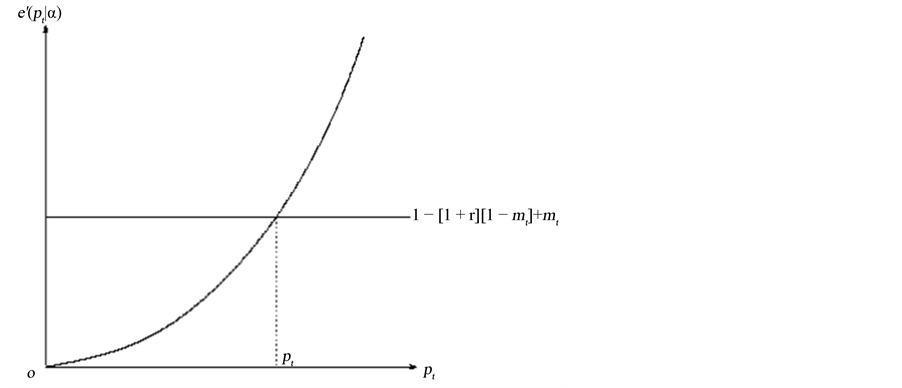
Figure 1. Optimal effort level.
expenditure is 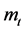 3.
3.
We assume that  is a decreasing function of
is a decreasing function of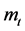 , or equivalently,
, or equivalently, 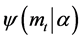 is an increasing function of
is an increasing function of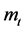 . This assumption means that the marginal increment of effort for raising the success probability cannot be canceled by a lowered interest rate offered under more favorable credit conditions. That is, the effective cost for raising the success probability increases with the probability itself4.
. This assumption means that the marginal increment of effort for raising the success probability cannot be canceled by a lowered interest rate offered under more favorable credit conditions. That is, the effective cost for raising the success probability increases with the probability itself4.
Assumption 1.
The equilibrium loan interest rate, 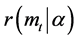 ,is a monotonously decreasing function of
,is a monotonously decreasing function of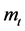 .
.
Employing the envelope theorem to Equation (4) and using the property of Equation (9) and Assumption 1, we obtain
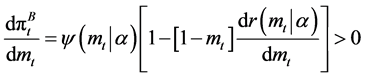 . (10)
. (10)
Consequently,
Theorem 1.
The instantaneous utility of a family, 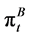 is a continuous and monotonously increasing function of the education expenditure,
is a continuous and monotonously increasing function of the education expenditure,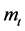 . Furthermore, there is a unique critical expenditure level
. Furthermore, there is a unique critical expenditure level  that satisfies
that satisfies
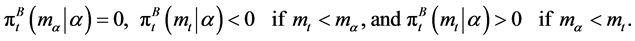 (11)
(11)
Proof. The intermediate value theorem validates the assertion based on Lemma1 and Equations (7) and (10).
Theorem 1 implies that even though an extended family has a lexicographic preference for its descendants’ wellbeing, no matter how wealthy it once was, its members are forever dispossessed of comfortable lives with modest income once its educational funds are depleted. Nevertheless, we must still analyze the effect of wealth accumulation on opportunities for enjoying a cultivated life. We consider this in the next section.
3. Intergenerational Wellbeing and Development in Pedagogical Skills
3.1. Wealth and Intergenerational Wellbeing
In this subsection, we analyze the relationship between a family’s wealth and intergenerational wellbeing (i.e., the sustainability of an educated extended family). This sustainability is defined as the probability of an extended family continuing to educate descendants and to enjoy cultivated lives forever.
To calculate this sustainability, let us denote 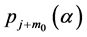 as the probability with which an extended family, which possesses
as the probability with which an extended family, which possesses 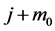 units of non-perishable goods, depletes its wealth and is dispossessed from cultivated life someday.
units of non-perishable goods, depletes its wealth and is dispossessed from cultivated life someday. 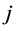 is a non-negative integer and
is a non-negative integer and 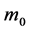 is the initial endowment, which is located at the vicinity of 1.
is the initial endowment, which is located at the vicinity of 1.
This problem is formulated as that of a random walk process, which is expressed by Equation (2), with the absorbing barrier at  5.
5.  satisfies the following difference equation. That is,
satisfies the following difference equation. That is,
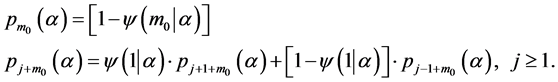 (12)
(12)
The solution of this difference equation is
 , (13)
, (13)
where 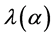 is the eigen-value of difference Equation (12) and is less than unity. Consequently, the sustainability of a family, which possesses
is the eigen-value of difference Equation (12) and is less than unity. Consequently, the sustainability of a family, which possesses 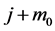 units of wealth,
units of wealth, 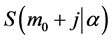 is
is
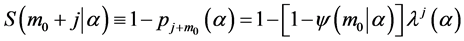 . (14)
. (14)
It is evident from Equation (14) that members of wealthier extended families can enjoy cultivated lives throughout time, since ![]() is a monotonously increasing function of
is a monotonously increasing function of 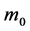 and
and . That is,
. That is,
Theorem 2.
The wealthier an extended family is, the higher the sustainability of its members enjoying cultivated lives becomes.
Equation (14) also suggests a theory of social stratification with random social mobility. Wealthier extended families rarely descend to the stratum that is bothered by daily life and is excluded from educational opportunities. Nevertheless, those who belong to a stratum whose income is located below 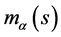 are entirely dispossessed of opportunities for ascending to the cultivated stratum, and consume income for ephemeral purposes that belong to the second priority in its lexicographic preference, even though they wish to educate their children. We emphasize that such seemingly selfish consumption of the non-wealthy stratum is not due to its shortage of love for children but due to its disillusionment owing to the shortage of educational funds.
are entirely dispossessed of opportunities for ascending to the cultivated stratum, and consume income for ephemeral purposes that belong to the second priority in its lexicographic preference, even though they wish to educate their children. We emphasize that such seemingly selfish consumption of the non-wealthy stratum is not due to its shortage of love for children but due to its disillusionment owing to the shortage of educational funds.
Such stratification can be regarded spuriously as the result of relative deprivation (Veblen [9] ; Merton [10] ) or of differences in social good (Krause [11] ). However, these sociological theories underestimate the effect of economic affluence. Relative deprivation emerges from income disparity. Many resources are poured into education for establishing a social good. That is, although relative deprivation and formation of an intrinsic social good come from an extended family’s economic affluence, sociological theories never succeed in explaining the cause of income disparity.
Our theory clarifies that imperfect information concerning the effort level of children plays a key role in income disparity. Even though a child in a non-wealthy family would strive to succeed, his/her efforts are unverifiable. The financial intermediary never validates his/her efforts because the effort level is unobservable and the family’s default cost is smaller under the principle of limited liability (we assume here that collateral for the loan is zero owing to humanitarian reasons6). Thus, non-wealthy families are excluded entirely from educational loan markets. This is an acute origin of income disparity.
3.2. Development of Pedagogical Skills and Intergenerational Wellbeing
In this subsection, we consider how development of pedagogical skills affects intergenerational wellbeing.
First, we calculate the effect of development of the skills to the minimally required fund  for education investment. By differentiating Equation (11) and applying the envelope theorem in Equation (4), we obtain
for education investment. By differentiating Equation (11) and applying the envelope theorem in Equation (4), we obtain
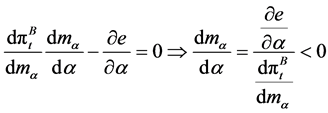 . (15)
. (15)
Thus, the minimal funds required for educational investment are reduced by development of pedagogical skills. To summarize,
Theorem 3.
Less wealthy families can access educational loan markets by development of pedagogical skills. This raises the intergenerational wellbeing of such families.
Such an egalitarian result is based on the fact that development of teachers’ skills enhances children’s efforts through stimulating their curiosity. This heightens the efficacy in education, and hence, financial intermediaries may grant educational loans even in cases in which a family is not so wealthy. Thus, development of pedagogical skills contributes to equalizing educational opportunities and enriching less wealthy families.
Second, we consider how the sustainability of an extended family is affected by the development of pedagogical skills. By differentiating Equation (5), it is evident that
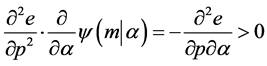 . (16)
. (16)
Hence, from Equation (13),  is a decreasing function of
is a decreasing function of![]() . Thus, Equation (14) implies that the sustainability of an extended family,
. Thus, Equation (14) implies that the sustainability of an extended family, ![]() , is an increasing function of
, is an increasing function of![]() . This is because development in pedagogical skills makes education more effective by advancing children’s intelligence abilities and raises the sustainability of extended families (i.e., intergenerational wellbeing). That is,
. This is because development in pedagogical skills makes education more effective by advancing children’s intelligence abilities and raises the sustainability of extended families (i.e., intergenerational wellbeing). That is,
Theorem 4.
Development of pedagogical skills heightens the sustainability of an extended family defined by Equation (14). Such skills contribute to enhancing intergenerational wellbeing.
3.3. Implications
There are serious implications in Theorem 4 concerning desired nature of pedagogical skills and wellbeing. Generally, it is considered that education should delve into how students can earn higher income regardless of their displeasure and different kinds of abilities. Instead of such existing human capital theory, we emphasize that the acute necessity for education is inspiring their various intellectual curiosity, which facilitate to induce students into their talented jobs. This effect is expressed  in Equation (3).
in Equation (3).
Such a change in education will enhance social division of labor, and thus, surely equalizes income distribution compared with the economy in which every student is educated towards the same kind of job and cut-throat competition in labor market is inevitable.
4. Concluding Remarks
This article analyzed how efficacy in education affects intergenerational wellbeing. We obtained the following results.
First, capital market imperfection, which comes from the inability to verify children’s efforts, is an acute cause of stratification. This is because those who can invest much money incur heavier losses when their investment fails and, thus, it is reasoned that they are diligent and have a higher success probability in education. For the same reason, a non-wealthy family is excluded from capital markets, and deprived of opportunities for education.
Second, when education becomes more effective owing to progress in pedagogical skills, less wealthy families are able to access capital markets. The development of teachers’ skills such that mutual communication between teacher and students is facilitated makes educational investment more effective, and this improves credit conditions for families. Accordingly, pedagogical skills play a key role in equalizing educational opportunities. In addition, high efficacy in education uniformly enhances the sustainability of extended families such that they can enjoy cultivated and affluent lives.
For these two reasons, pedagogical skills are of profound social significance.
References
- Otaki, M. (2014) Income Disparity, Uneven Economic Opportunities, and Verifiability. Advances in Social Sciences Research Journal, 1, 44-49.
- Arrow, K.J. (1963) Uncertainty and the Welfare Economics of Medical Care. American Economic Review, 53, 941- 873.
- Stiglitz, J.E. and Weiss, A. (1981) Credit Rationing in Markets with Imperfect Information. American Economic Review, 71, 393-410.
- Dewey, J. (1916) Democracy and Education. Macmillan, London.
- Deere, D.R. and Vosovic, J. (2006) Educational Wage Premiums and the U.S. Income Distribution: A Survey. In: Hanuschek, E. and Welch, F. Eds., Hand Book of Educational Economics Vol. 1, North-Holland, Amsterdam, Netherland, 253-306.
- Mankiw, N.G., Romer, D. and Weil, N. (1992) A Contribution to the Empirics of Economic Growth. Quarterly Journal of Economics, 106, 407-437. http://dx.doi.org/10.2307/2118477
- Ito, S. (2014) Child Labor and Education Policies, Institute of Developing Economies-Japan External Trade Organization. http://www.ide.go.jp/Japanese/Research/Theme/Soc/Child_labor/index.html
- Cox, D.R. and Miller, H.D. (1965) The Theory of Stochastic Process. Chapman & Hall, London.
- Veblen, T. (1899) The Theory of the Leisure Class: An Economic Study of Institution. Macmillan, London.
- Merton, R.K. (1949) On Theoretical Sociology. The Free Press, New York.
- Krauss, I. (1976) Stratification, Class, and Conflict. The Free Press, New York.
- Johnston, D.B. (2001) The Economics and Politics of Income Contingent Repayment Plans. The International Higher Education Finance and Accessibility Project, State University of New York, Buffalo.
NOTES

1According to Dewy , “To the one who is learned, subject matter is extensive, accurately defined, and logically interrelated. To one who is learning, it is fluid, partial, and connected through his personal occupations. The problem of teaching is to keep the experience of the student moving in the direction of what the expert already knows. Hence, the need that the teacher know both subject matter and the characteristic needs and capacities of the student.”
2As Deer and Vesovic summarize, the main concern of educational economists is how educational investment affects one’s income and/ or wealth. However, we must note that quality of education symbolized by scholastic skills correlate with the fruits of education, although such skills are hardly measurable.

3Whenever ![]() is the boundary such that
is the boundary such that , any financial intermediary does not offer a loan.
, any financial intermediary does not offer a loan.
4By differentiating Equation (5) with consideration for the relationship in Equation (9), we obtain
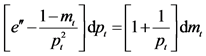 .
.
Thus, it is clear that Assumption 1 is validated for the affluent class, which can commit more deeply to educational investment (i.e.,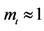 ).
).

5See Cox and Miller for more detail.
6As Johnson argues, income contingent repayment (a kind of equity finance) might be desirable. However, this is not a prevalent type of contract. Equity finance is generally an unsuitable measure under an asymmetric information structure. For more detail, see Jensen .

