Theoretical Economics Letters
Vol.4 No.2(2014), Article ID:43729,9 pages DOI:10.4236/tel.2014.42022
Dynamic Monopoly with Demand Delay
Akio Matsumoto1, Ferenc Szidarovszky2
1Department of Economics, Chuo University, Tokyo, Japan
2Department of Applied Mathematics, University of Pécs, Pécs, Hungary
Email: akiom@tamacc.chuo-u.ac.jp, szidarka@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 26 December 2013; revised 26 January 2014; accepted 2 February 2014
ABSTRACT
This study analyses the dynamics of nonlinear monopoly. To this end, the conventional assumptions in the text-book monopoly are modified; first, the complete information on the market is replaced with the partial information; second, the instantaneous information is substituted by the delay information. As a result, since such a monopoly is unable to jump, with one shot, to the optimal point for which the profit is maximized, the monopoly has to search for it. In a continuoustime framework, the delay destabilizes the otherwise stable monopoly model and generates cyclic oscillations via a Hopf bifurcation. In a discrete-time framework, the steady state bifurcates to a bounded oscillation via a Neimark-Sacker bifurcation. Although this has been only an introduction of delay into the traditional monopoly model, it is clear that the delay can be a source of essentially different behavior from those of the nondelay model.
Keywords:Monopolist Competition; Demand Fluctuations; Bounded Rationality; Fixed Time Delay; Continuous and Discrete Dynamics

1. Introduction
Implicit in the text-book monopoly is an assumption of complete and instantaneous information or knowledge available to economic agents at free of charge. Under such circumstances, knowing the certain price and cost functions, the monopolist can make an optimal decision of price and output to maximize its profit and realize it. As a result, the text-book monopoly model becomes static in nature. There are, however, many empirical works to indicate that such an assumption of rational economic agents goes too far. In reality the monopolist is boundedly rational and adjusts its price and output as a function of its limited knowledge and past experiences. To fill this gap, we propose, in this study, to relax this assumption and develop a dynamic monopoly model. In particular, we assume first that the monopolist has only partial information about the market condition and second that the monopolist obtains it with time delay. In natural consequence of these alternations, the monopolist cannot jump to the optimal point but searches for it with using the actual data obtained through the market. The modified model becomes dynamic in nature. This is the issue far outside the scope of the text book monopoly and it is what we will consider in this study.
In the recent literature, various learning processes of the boundedly rational monopolist have been extensively studied. Puu [1] constructs a discrete-time monopoly model in which price function is cubic and cost function is linear. It is shown that the gradient learning or search process based on locally obtained information might behave in an erratic way under the condition that the price function has an inflection point. Assuming that the monopolist uses a rule of thumb to determine quantity to produce, Naimzada and Ricchiuti [2] reconsider Puu’s model with a linear cost function and a cubic price function without the inflection point. Their model is then generalized by Asker [3] who replaces the cubic function with higher-order polynomials. Matsumoto and Szidarovszky [4] further generalize Asker’s model by introducing the more general type of the cost function. Since those models are described by one dimensional difference equation, chaotic dynamics can arise via period-doubling bifurcation.
In this study we reconsider a dynamic monopoly model from two different points of view. First, to detect the effect caused by non-instantaneous information, the dynamic process is constructed in continuous-time scales and a fixed time delay is introduced. Second, we discretize the continuous process to obtain a “delay” discrete process and analyze the delay effect on discrete dynamics. In both models, local stability of a stationary state is analytically considered and global dynamics is numerically examined.
The paper is organized as follows. In Section 2, the delay differential model is presented and stability switch is considered. In Section 3, the delay difference model is constructed to give rise to the emergence of NeimarkSacker bifurcation. And finally, Section 4 concludes the paper.
2. Delay Differential Dynamics
Consider a single product monopoly that sells its product to a homogeneous market. Let 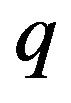 denote the output of the firm,
denote the output of the firm, 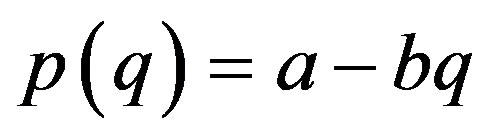 the price function and
the price function and 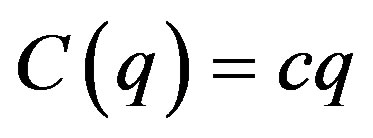 the cost function1. Since
the cost function1. Since  and
and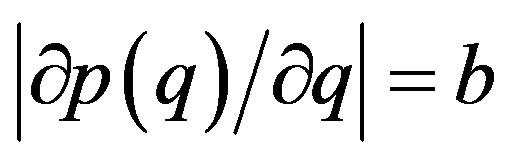 , we call
, we call  the maximum price and
the maximum price and 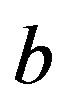 the marginal price. There are many ways to introduce uncertainty into this framework by considering
the marginal price. There are many ways to introduce uncertainty into this framework by considering ,
, 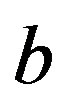 or
or  uncertain. In this study, it is assumed that the firm knows the marginal price and the marginal cost but does not know the maximum price. In consequence it has only an estimate
uncertain. In this study, it is assumed that the firm knows the marginal price and the marginal cost but does not know the maximum price. In consequence it has only an estimate 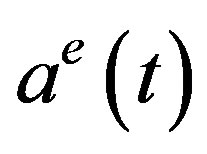 of it at each time period. So the firm believes that its profit is
of it at each time period. So the firm believes that its profit is
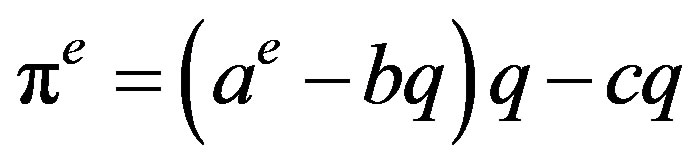 its best response is
its best response is
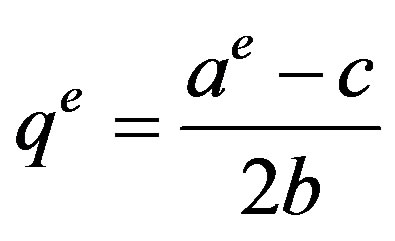
and the firm expects the market price to be
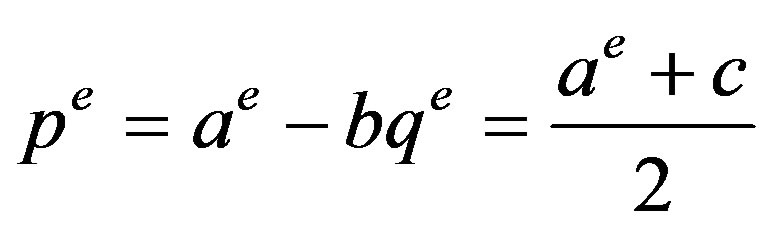 . (1)
. (1)
However, the actual market price is determined by the real price function
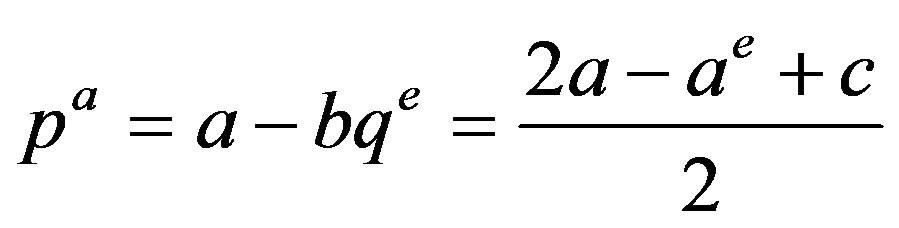 . (2)
. (2)
Using these price data, the firm updates its estimate. The simplest way for adjusting the estimate is the following. If the actual price is higher than the expected price, then the firm shifts its believed price function by increasing the value of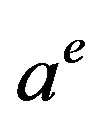 , and if the actual price is the smaller, then the firm decreases the value of
, and if the actual price is the smaller, then the firm decreases the value of . If the two prices are the same, then the firm wants to keep its correct estimate of the maximum price. This adjustment or learning process can be modeled by the following differential equation:
. If the two prices are the same, then the firm wants to keep its correct estimate of the maximum price. This adjustment or learning process can be modeled by the following differential equation:
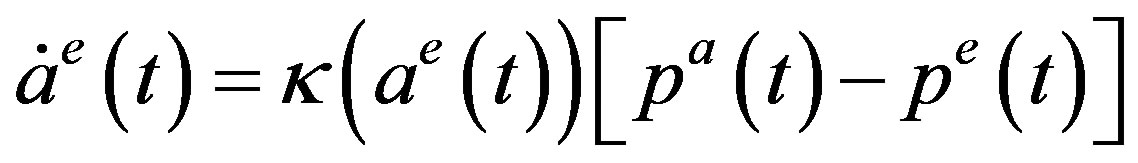 where
where 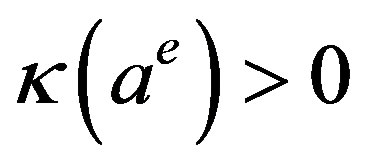 is the speed of adjustment. Substituting relations (1) and (2) gives the adjustment equation as a differential equation with respect to
is the speed of adjustment. Substituting relations (1) and (2) gives the adjustment equation as a differential equation with respect to :
:
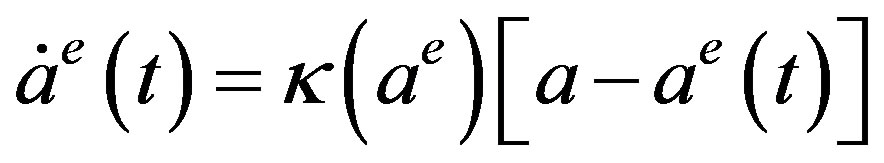 . (3)
. (3)
For analytical simplicity, we assume that
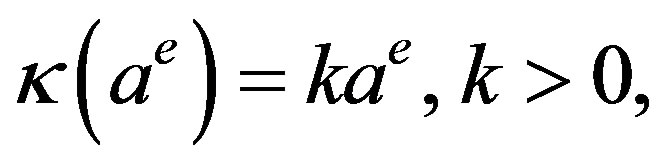
so Equation (3) is reduced to the logistic equation,
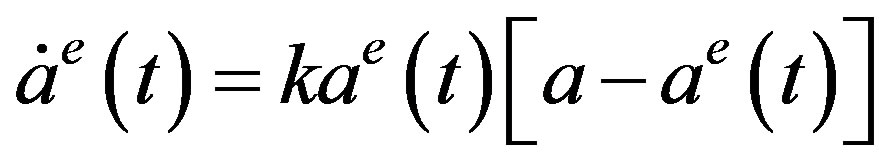 (4)
(4)
which is a nonlinear differential equation. Notice that Equation (4) has two steady states,  and
and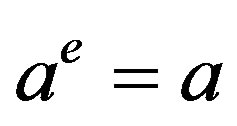 . Small perturbation from
. Small perturbation from 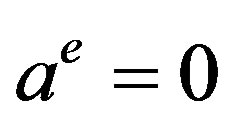 satisfies the linear equation
satisfies the linear equation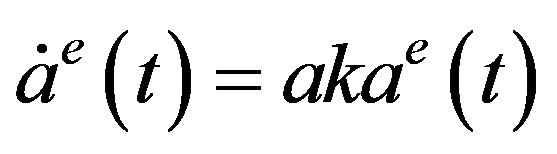 , which shows that
, which shows that 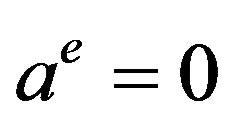 is unstable with exponential growth. We thus only need to consider the stability of the positive steady state
is unstable with exponential growth. We thus only need to consider the stability of the positive steady state . The steady state corresponds to the true value of the maximum price.
. The steady state corresponds to the true value of the maximum price.
If there is a time delay 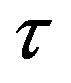 in the estimated price, then Equation (4) has to be modified as
in the estimated price, then Equation (4) has to be modified as
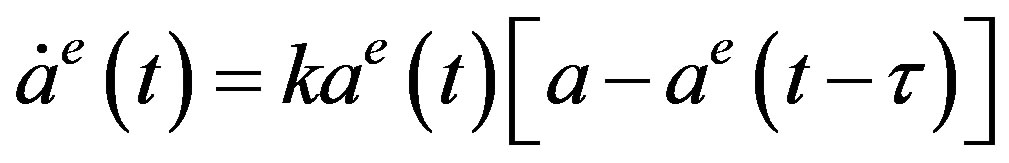 . (5)
. (5)
By introducing the new variable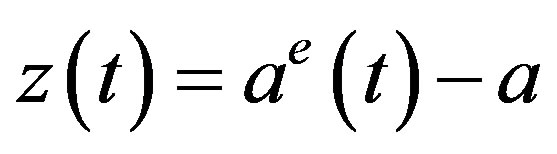 , the linearized version of Equation (5) becomes
, the linearized version of Equation (5) becomes
 (6)
(6)
where . As a benchmark for stability analysis, we start with the no-delay case. If there is no delay,
. As a benchmark for stability analysis, we start with the no-delay case. If there is no delay, 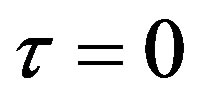 , then Equation (6) becomes an ordinary differential equation with characteristic polynomial
, then Equation (6) becomes an ordinary differential equation with characteristic polynomial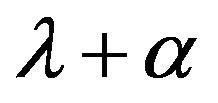 . So the only eigenvalue is negative implying the local asymptotic stability. If
. So the only eigenvalue is negative implying the local asymptotic stability. If , then the exponential form
, then the exponential form 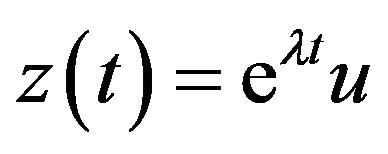 of the solution reduces the characteristic equation to the following form:
of the solution reduces the characteristic equation to the following form:
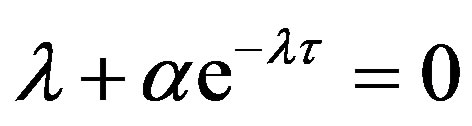 . (7)
. (7)
This is a transcendental equation. Notice that the only eigenvalue is negative when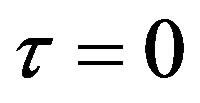 . Notice also that
. Notice also that  is not a solution of Equation (7). For sufficiently small deviation of
is not a solution of Equation (7). For sufficiently small deviation of 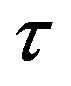 from zero, the real parts of the eigenvalues are still negative by continuity. We seek conditions of
from zero, the real parts of the eigenvalues are still negative by continuity. We seek conditions of  such that the real parts change from negative to positive. Since stability is changed to instability under this condition, it is often called stability switch. At this critical value of
such that the real parts change from negative to positive. Since stability is changed to instability under this condition, it is often called stability switch. At this critical value of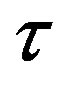 , the characteristic equation must have a pair of purely imaginary eigenvalues,
, the characteristic equation must have a pair of purely imaginary eigenvalues, . If
. If 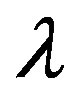 is an eigenvalue, then its complex conjugate is also an eigenvalue. So, without loss of generality, we can assume that
is an eigenvalue, then its complex conjugate is also an eigenvalue. So, without loss of generality, we can assume that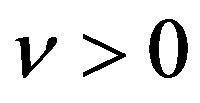 . So Equation (7) can be written as
. So Equation (7) can be written as
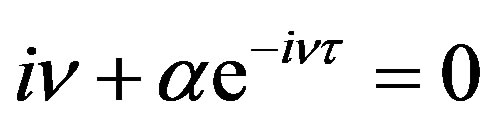 .
.
Separating the real and imaginary parts, we obtain
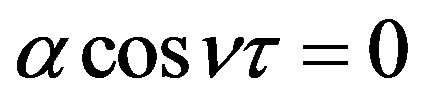
and
 .
.
Therefore
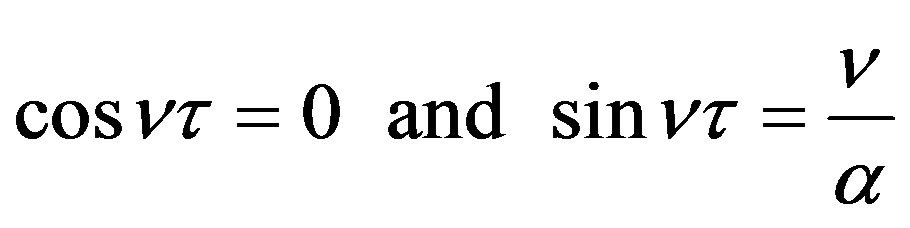
implying that  leading to infinitely many solutions,
leading to infinitely many solutions,
 (8)
(8)
The solution  with
with 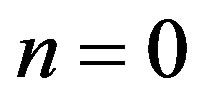 forms a downward-sloping curve with respect to
forms a downward-sloping curve with respect to ,
,
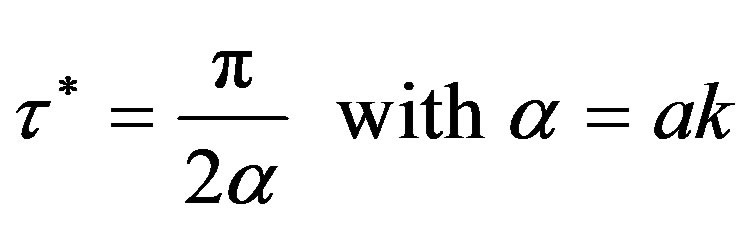
Applying the main theorem in Hayes [5] or the same result obtained differently in Matsumoto and Szidarovszky [6] , we can find that this curve divides the non-negative 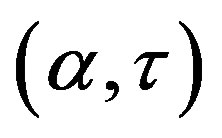 plane into two subregions; the real parts of the roots of the characteristic equation are all negative in the region below the curve and for some roots are positive in the region above. This curve is often called the partition curve separating the stability region from the instability region. Notice that the critical value of
plane into two subregions; the real parts of the roots of the characteristic equation are all negative in the region below the curve and for some roots are positive in the region above. This curve is often called the partition curve separating the stability region from the instability region. Notice that the critical value of  decreases with
decreases with 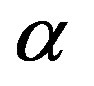 so a larger value of
so a larger value of 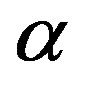 caused by the high speed of adjustment and/or the larger maximum price makes the steady state less stable.
caused by the high speed of adjustment and/or the larger maximum price makes the steady state less stable.
We can easily prove that all pure complex roots of Equation (7) are single. If 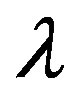 is a multiple eigenvalue, then it must solve equations
is a multiple eigenvalue, then it must solve equations
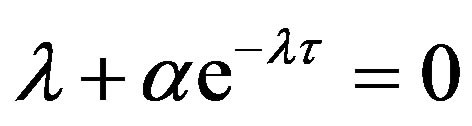
and
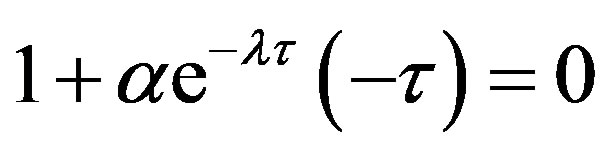 .
.
Based on the first equation, the second equation becomes
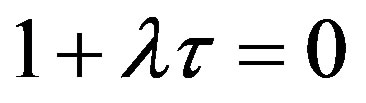
or
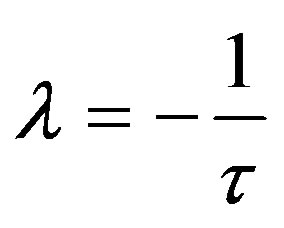
implying that 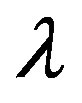 becomes a real negative value which contradicts the assumption that it is purely imaginary.
becomes a real negative value which contradicts the assumption that it is purely imaginary.
In order to detect stability switches and the emergence of Hopf bifurcation, we select  as the bifurcation parameter and consider
as the bifurcation parameter and consider 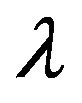 as function of
as function of ,
, . By implicitly differentiating Equation (7) with respect to
. By implicitly differentiating Equation (7) with respect to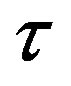 , we have
, we have
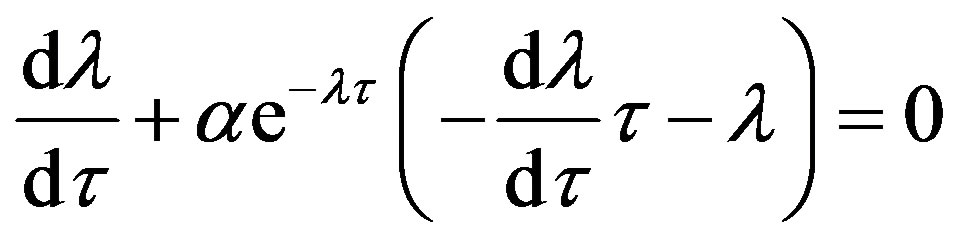
implying that
 .
.
With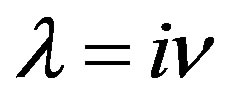 ,
,
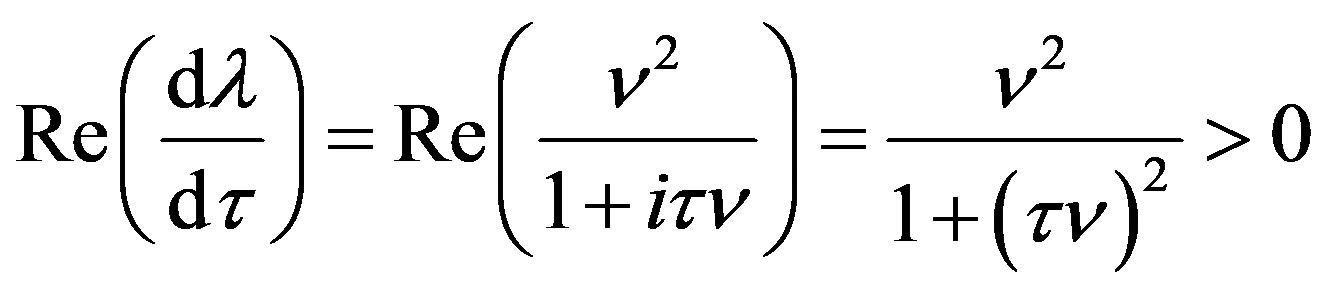 .
.
So the sign of the real part of an eigenvalue changes from negative to positive and it is a Hopf bifurcation point of the nonlinear learning process (5) with one delay. Thus we have the following result.
Theorem 1: For the logistic adjustment process (5), the steady state is locally asymptotically stable if 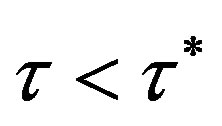 and locally unstable if
and locally unstable if 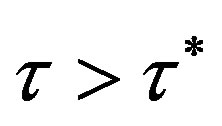 Hopf bifurcation occurs if
Hopf bifurcation occurs if 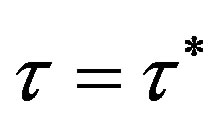 and a stable limit cycle exist for
and a stable limit cycle exist for  where
where
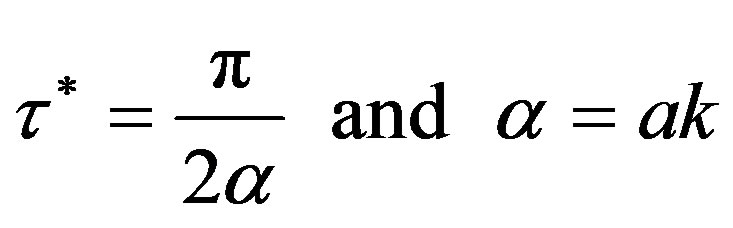 .
.
The delay logistic adjustment process can have periodic solutions for a large range of value of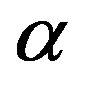 , the product of the maximum price
, the product of the maximum price  and the adjustment coefficient
and the adjustment coefficient . The period of the solution at the critical delay value is
. The period of the solution at the critical delay value is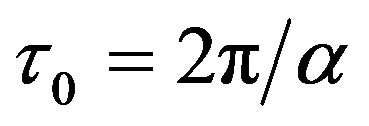 , which is
, which is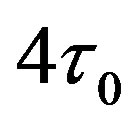 .
.
An intuitive reason why stability switch occurs only at the critical value of 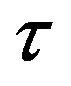 with
with  is the following. Notice first that the delay differential equation has infinitely many eigenvalues and second that their real parts are all negative for
is the following. Notice first that the delay differential equation has infinitely many eigenvalues and second that their real parts are all negative for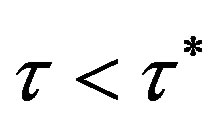 . When increasing
. When increasing  arrives at the partition curve, then the real part of one eigenvalue becomes zero and its derivative with respect to
arrives at the partition curve, then the real part of one eigenvalue becomes zero and its derivative with respect to 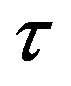 is positive implying that the real part changes its sign to positive from negative. Hence the steady state loses stability at this critical value. Further increasing
is positive implying that the real part changes its sign to positive from negative. Hence the steady state loses stability at this critical value. Further increasing 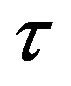 crosses the
crosses the 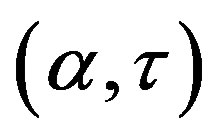 curve defined by Equation (8) with
curve defined by Equation (8) with 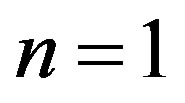 where the real part of another eigenvalue changes its sign to positive from negative. Repeating the same arguments, we see that at each intersection one more eigenvalue changes its real part from negative to positive, so stability cannot be regained and therefore no stability switch occurs for any
where the real part of another eigenvalue changes its sign to positive from negative. Repeating the same arguments, we see that at each intersection one more eigenvalue changes its real part from negative to positive, so stability cannot be regained and therefore no stability switch occurs for any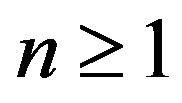 . Hence stability is changed only when
. Hence stability is changed only when 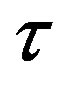 crosses the partition curve.
crosses the partition curve.
Theorem 1 is numerically confirmed. Given , a bifurcation diagram with respect to
, a bifurcation diagram with respect to  is depicted in Figure 1(a). It is seen that the steady state loses stability at
is depicted in Figure 1(a). It is seen that the steady state loses stability at  and bifurcates to a cyclic oscillation for
and bifurcates to a cyclic oscillation for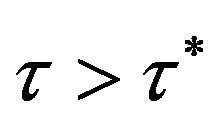 . In addition, given
. In addition, given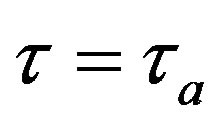 , Figure 1(a) indicates the maximum and the minimum values of the trajectory are denoted by
, Figure 1(a) indicates the maximum and the minimum values of the trajectory are denoted by 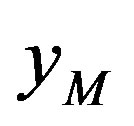 and
and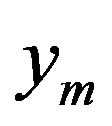 . Figure 1(b) illustrates a limit cycle having the same extremum in the phase plane.
. Figure 1(b) illustrates a limit cycle having the same extremum in the phase plane.
We can discuss another delay adjustment process that is a hybrid of Equations (4) and (5),
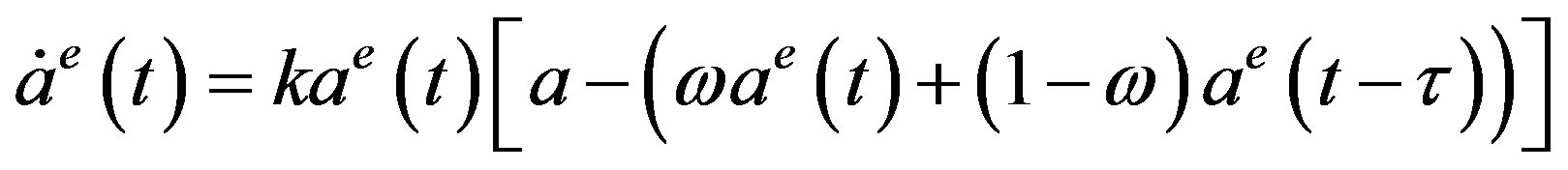 (9)
(9)
where  is a positive constant less than unity. It can be seen that Equation (9) is reduced to Equation (4) when
is a positive constant less than unity. It can be seen that Equation (9) is reduced to Equation (4) when  goes to unity and to Equation (5) when
goes to unity and to Equation (5) when  goes to zero. The steady state of Equation (9) is equal to the maximum price and thus the same as the one of Equation (4) as well as Equation (5). The linearized equtaion becomes
goes to zero. The steady state of Equation (9) is equal to the maximum price and thus the same as the one of Equation (4) as well as Equation (5). The linearized equtaion becomes
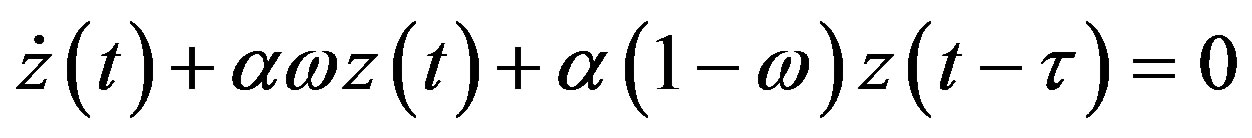
and its characteristic equation is
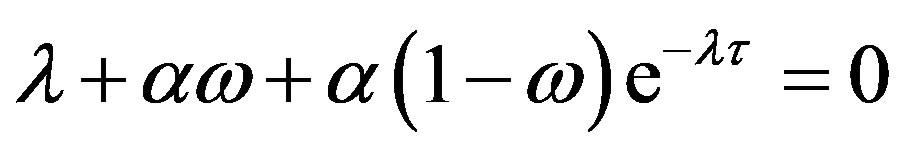 .
.
Using the similar arguments, we can obtain the results including that the delay becomes harmless if the instanteneous term 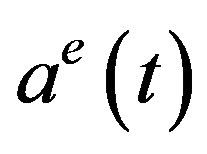 is dominant in Equation (9):
is dominant in Equation (9):
Theorem 2: 1) If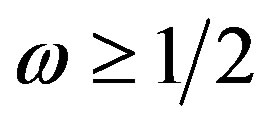 , then the steady state of the hybrid logistic adjustment process (9) is locally asymptotically stable for all delay
, then the steady state of the hybrid logistic adjustment process (9) is locally asymptotically stable for all delay ; 2) if
; 2) if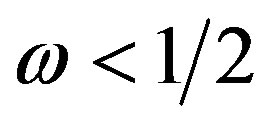 , then the steady state is locally asymptotically stable if
, then the steady state is locally asymptotically stable if , loses stability for
, loses stability for 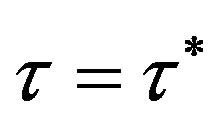 and bifurcates to a limit cycle via a Hopf bifurcation if
and bifurcates to a limit cycle via a Hopf bifurcation if 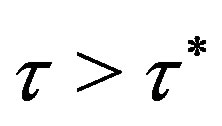 where
where
 .
.
3. Delay Discrete Dynamics
Our concern in this section is on how the different choice of the time scale affects dynamics examined in the previous section. Toward this end, we discretize the delay differential Equation (4) by replacing 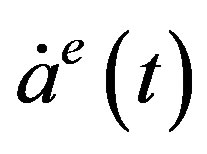 with
with 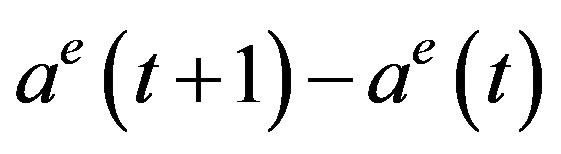 to obtain
to obtain
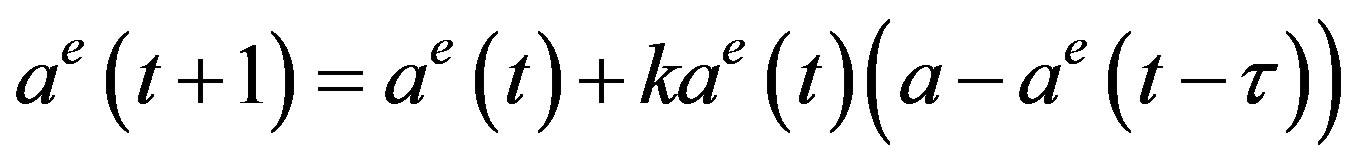 (10)
(10)
and then reconsider local and global dynamics in discrete time. The positive steady state of Equation (5) remains as a steady state of this difference equation. We mention that this discrete-time equation has a 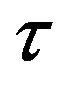 -step
-step delay
delay
 (a)
(a)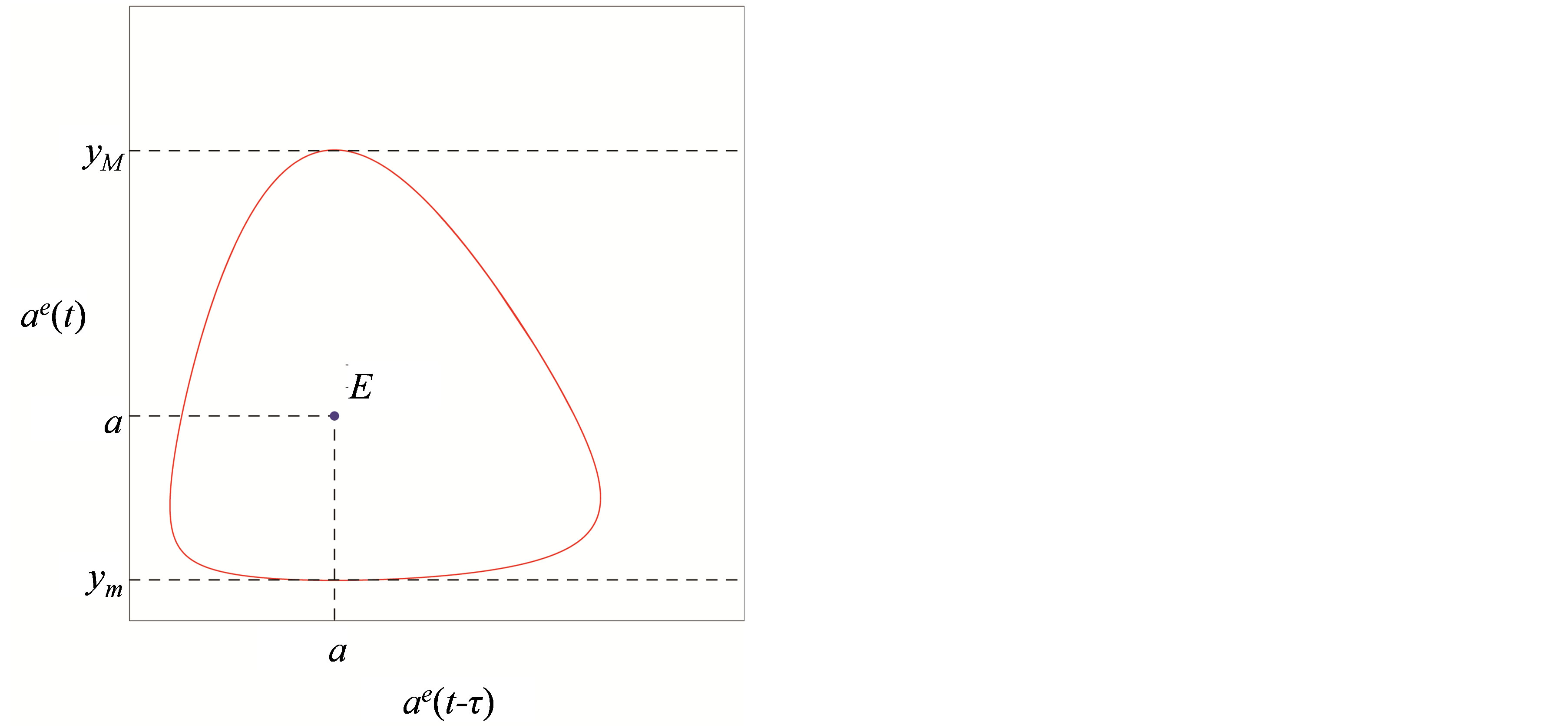 (b)
(b)
Figure 1. Cyclic oscillations for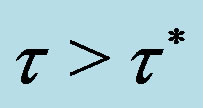 . (a) Bifurcation diagram; (b) Limit cycle with
. (a) Bifurcation diagram; (b) Limit cycle with .
.
when 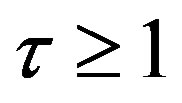 2. The remaining of this section starts with the case of
2. The remaining of this section starts with the case of 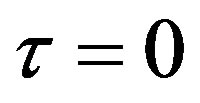 and then, proceed the cases of
and then, proceed the cases of 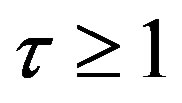 in detail to concentrate on delay effects in the discrete-time framework.
in detail to concentrate on delay effects in the discrete-time framework.
If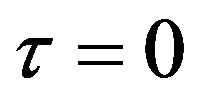 , then Equation (10) becomes a nonlinear first-order difference equation
, then Equation (10) becomes a nonlinear first-order difference equation
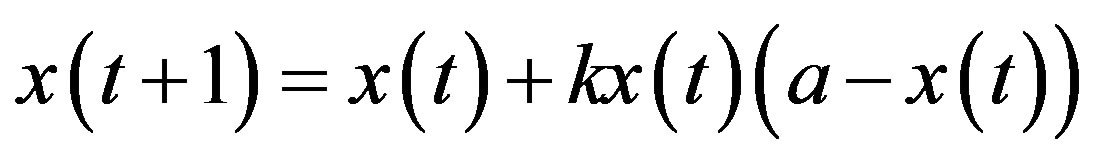 (11)
(11)
where we introduce the new variable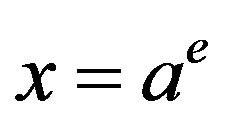 . Changing the variable again by
. Changing the variable again by

reveals that Equation (11) can be reduced to the familiar form,
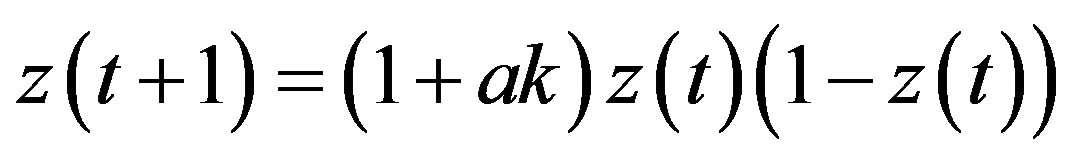 .
.
It is now well known that the logistic equation can generate wide variety of dynamics ranging from a periodic cycle to chaos according to the specification of the coefficient 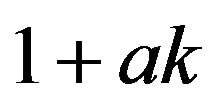 if the steady state is locally unstable.
if the steady state is locally unstable.
If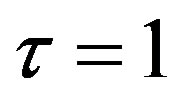 , then Equation (10) has one-step delay and then becomes a nonlinear second-order difference equation
, then Equation (10) has one-step delay and then becomes a nonlinear second-order difference equation
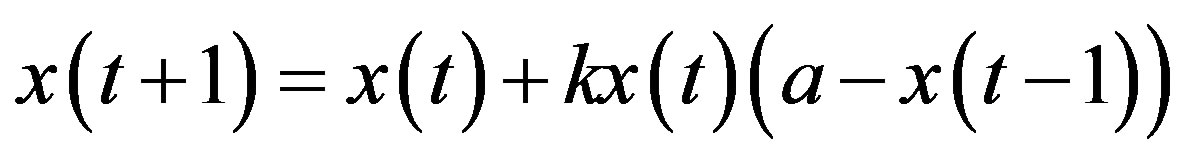 (12)
(12)
which can be converted to an equivalent 2D system of first-order difference equations,
 (13)
(13)
The linearized system around the steady state  is
is

where the subscript 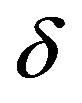 implies that the variable with this subscript is the difference between its value and the steady state. The characteristic equation is transformed into a quadratic equation,
implies that the variable with this subscript is the difference between its value and the steady state. The characteristic equation is transformed into a quadratic equation,
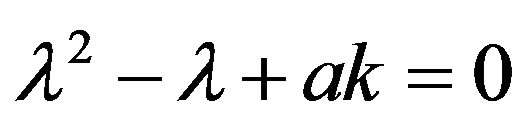 . (14)
. (14)
The following three conditions imply that the quadratic polynomial  has roots inside the unit cycle,
has roots inside the unit cycle,
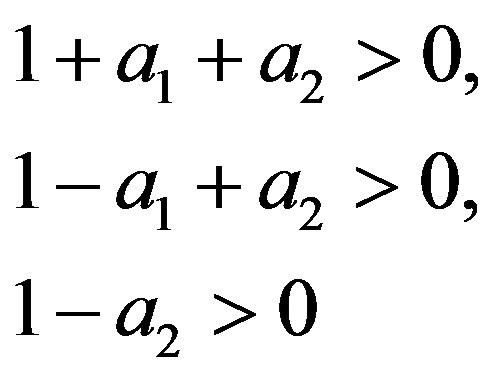 (15)
(15)
where
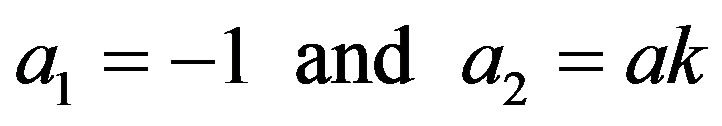 .
.
The first and second conditions of Equation (15) are always satisfied and so is the third condition if and only if 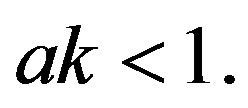
Taking 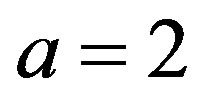 and selecting
and selecting 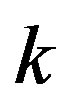 as the bifurcation parameter, we illustrate the bifurcation diagram in Figure 2(a) in which stability of the steady state is changed to instability at
as the bifurcation parameter, we illustrate the bifurcation diagram in Figure 2(a) in which stability of the steady state is changed to instability at 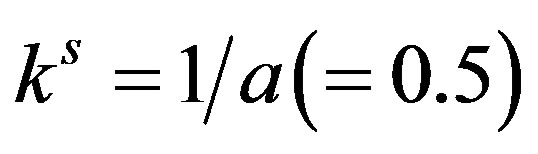 and cyclic behavior emerges for
and cyclic behavior emerges for 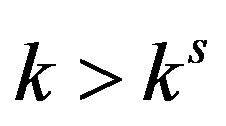 When
When 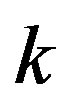 arrives at
arrives at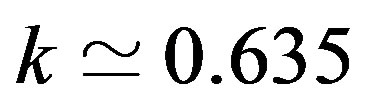 , the non-negativity condition is violated resulting in the birth of economically uninteresting behavior.
, the non-negativity condition is violated resulting in the birth of economically uninteresting behavior.
We further extend our analysis to a two-step delay (i.e., ) where the marginal revenue includes the delayed information obtained at period
) where the marginal revenue includes the delayed information obtained at period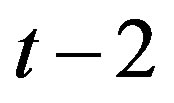 . The dynamic Equation (10) is now a third-order difference equation,
. The dynamic Equation (10) is now a third-order difference equation,
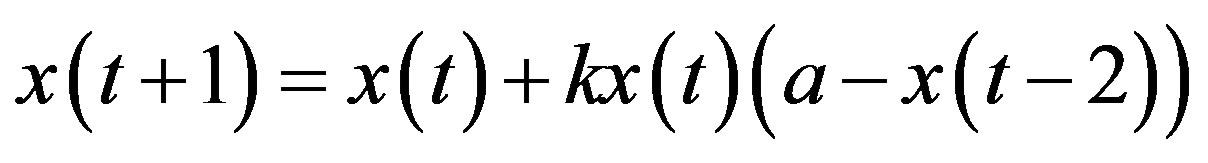 . (16)
. (16)
This can be written as a 3D system of first-order difference equations
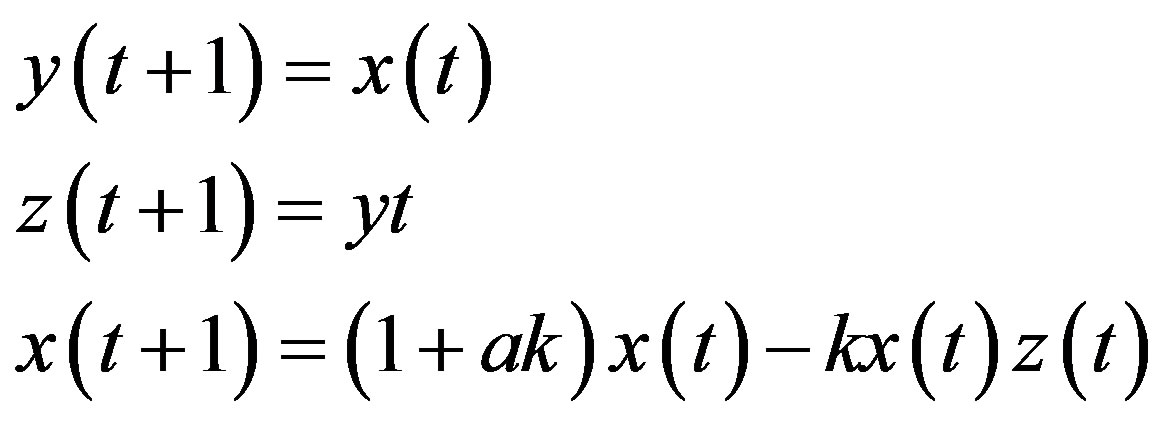 (17)
(17)
where the steady state is 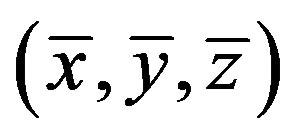 with
with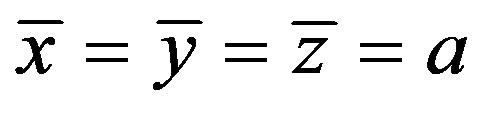 . Linear approximation of Equations (17) yields the linearized system having the form
. Linear approximation of Equations (17) yields the linearized system having the form
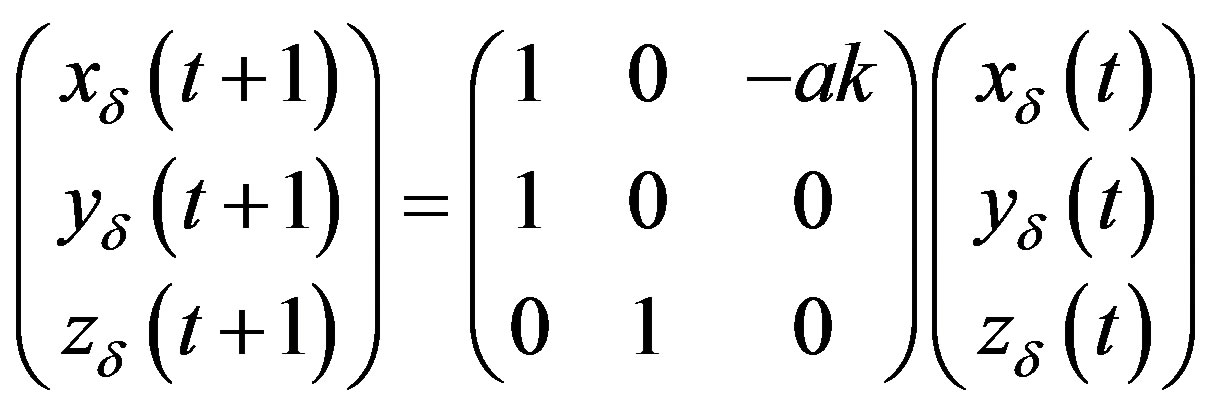 (18)
(18)
and the corresponding characteristic equation is cubic,
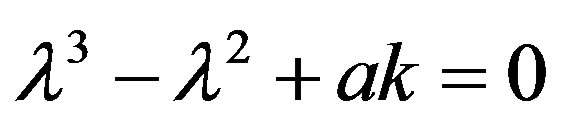 . (19)
. (19)
The steady state is locally asymptotically stable if all eigenvalues of Equation (19) are less than unity in absolute value. Farebrother [7] has proved that the most simplified form of the sufficient and necessary conditions for the cubic equation 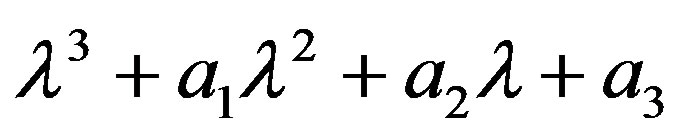 to have roots only inside the unit cycle are
to have roots only inside the unit cycle are
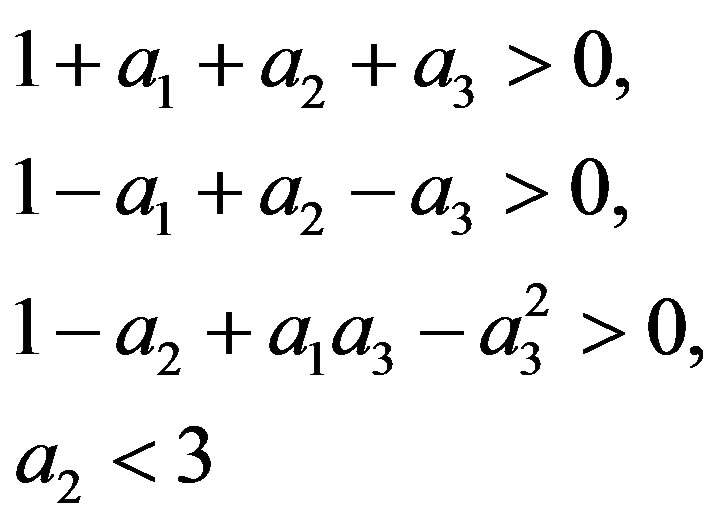 (20)
(20)
where

It can be verified that the first and fourth conditions are always satisfied while the second and third condition holds if
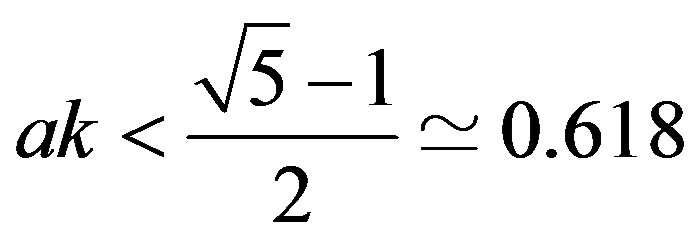 .
.
The bifurcation diagram with 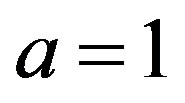 is illustrated in Figure 2(b), where
is illustrated in Figure 2(b), where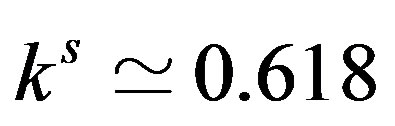 . It can be seen that Hopf bifurcation emerges for
. It can be seen that Hopf bifurcation emerges for .
.
If , then the characteristic equation is
, then the characteristic equation is 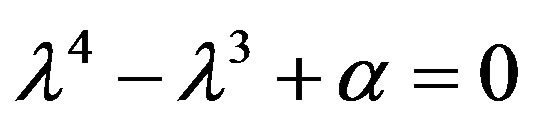 with
with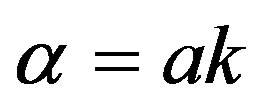 . For the quartic equation
. For the quartic equation
 (a)
(a) (b)
(b)
Figure 2. Bifurcation diagrams with different steps, (a) 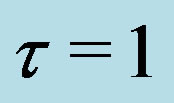 and
and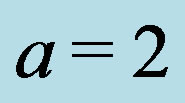 ; (b)
; (b) 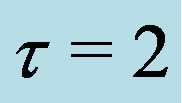 and
and .
.
the sufficient and necessary condition that all roots are inside the unit circle are (see Farebrother, [7] ) as follows:
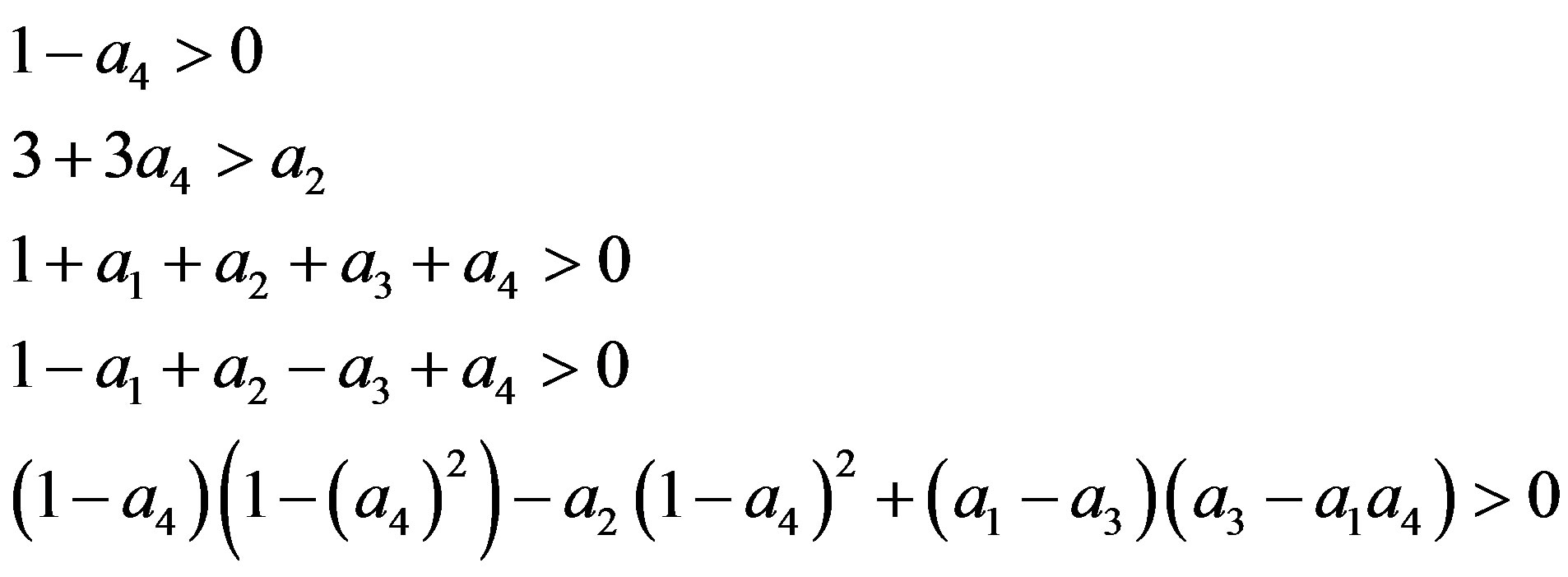
To our case, 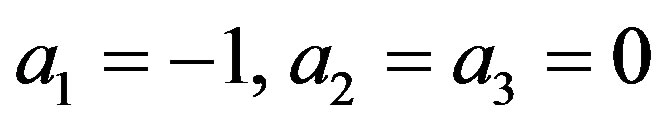 and
and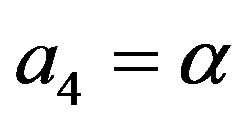 . The first four conditions are clearly satisfied if
. The first four conditions are clearly satisfied if  and the last condition can be reduced to the following:
and the last condition can be reduced to the following:
 .
.
Clearly
 .
.
Since 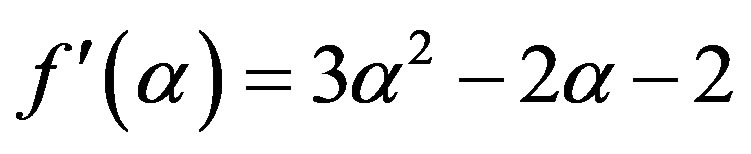 having two roots
having two roots
 ,
,
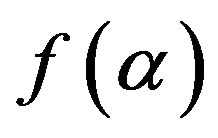 increases in intervals
increases in intervals 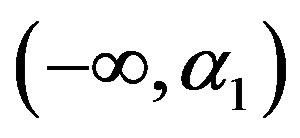 and
and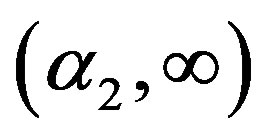 , and decreases in
, and decreases in . Notice that
. Notice that  and
and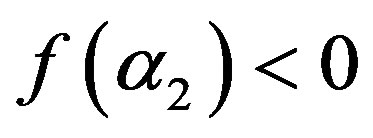 , so
, so  has three real roots: one is negative, two positive in intervals
has three real roots: one is negative, two positive in intervals 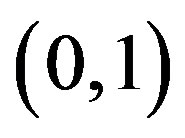 and
and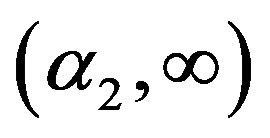 . Since
. Since 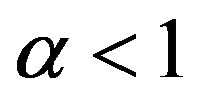 and the smallest positive root is approximately
and the smallest positive root is approximately  3, the stability condition is
3, the stability condition is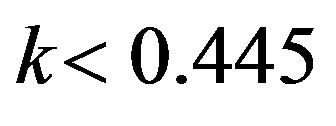 . It is numerically confirmed that the steady state is violated via Neimark-Sacker bifurcation for
. It is numerically confirmed that the steady state is violated via Neimark-Sacker bifurcation for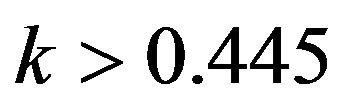 . Although the critical values
. Although the critical values 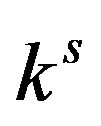 seem to decrease as the value of
seem to decrease as the value of 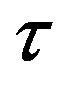 increases,
increases,
 this fact has not been analytically confirmed yet.
this fact has not been analytically confirmed yet.
Applying the same argument to the case of the general case, we have the adjustment process described by a
we have the adjustment process described by a 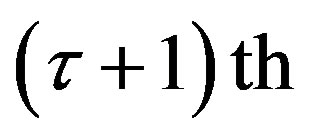 -order difference equation,
-order difference equation,
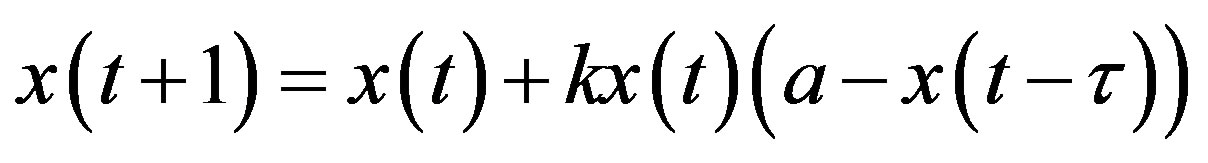
and a 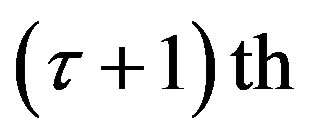 -order characteristic equation,
-order characteristic equation,
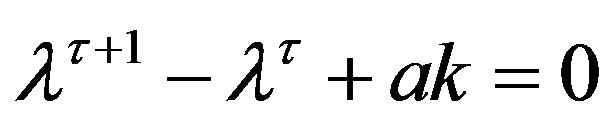
For a larger value of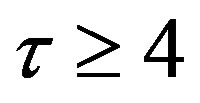 , we do not have the simplifed stability condition but the Samuelson or the CohnSchur conditions for the
, we do not have the simplifed stability condition but the Samuelson or the CohnSchur conditions for the 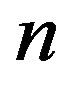 -th order equation can be applied to determine the critical value of
-th order equation can be applied to determine the critical value of 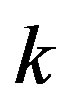 for the birth of Neimark-Sacker bifurcation4. We summarize the main result on the delay difference adjustment process:
for the birth of Neimark-Sacker bifurcation4. We summarize the main result on the delay difference adjustment process:
Theorem 3: Given the maximum price, the discrete-time adjustment process (10) has the critical value of the adjustment coefficient 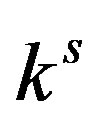 and the steady state is locally asymptotically stable if
and the steady state is locally asymptotically stable if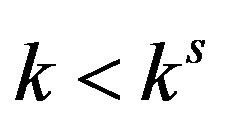 , loses stability for
, loses stability for 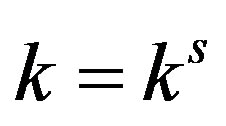 and bifurcates to a limit cycle via Neimark-Sacker bifurcation if
and bifurcates to a limit cycle via Neimark-Sacker bifurcation if .
.
4. Concluding Remarks
In this study, we analyzed the delay dynamics of a nonlinear monopoly. Two conventional assumptions in the traditional monopoly model are modified: the information obtained from the market is assumed to be limited and delayed. As a natural consequence, the monopoly is unable to jump, with one shot, to the optimal point but revises its decision by taking transaction data experiences obtained from the market into account. In either the continuous-time framework or the discrite-time framwork, the steady state is locally asymptotically stable for the smaller values of delay and bifurcates to a limit cycle via a Hopf bifurcation in the continuous-time framework and via a Neimark-Sacker bifurcation in the discrete-time framework for the larger values. Delay monopoly generates very different dynamics than those of the text-book monopoly.
Acknowledgements
The authors highly appreciate the financial supports from the MEXT-Supported Program for the Strategic Research Foundation at Private Universities 2013-2017, the Japan Society for the Promotion of Science (Grant-in-Aid for Scientifc Research (C) 24530201 and 25380238) and Chuo University (Grant for Special Research). The usual disclaimers apply.
References
- Puu, T. (1995) The Chaotic Monopolist. Chaos, Solitions and Fractals, 5, 35-44. http://dx.doi.org/10.1016/0960-0779(94)00206-6
- Naimzada, A.K. and Ricchiuti, G. (2008) Complex Dynamics in a Monopoly with a Rule of Thumb. Applied Mathematics and Computation, 203, 921-925. http://dx.doi.org/10.1016/j.amc.2008.04.020
- Asker, S.S. (2013) On Complex Dynamics of Monopoly Market. Economic Modeling, 31, 586-589. http://dx.doi.org/10.1016/j.econmod.2012.12.025
- Matsumoto, A. and Szidarovszky, F. (2013) Complex Dynamics of Monopolies with Gradient Adjustment. IERCU DP # 209, Institute of Economic Research, Chuo University.
- Hayes, N.D. (1950) Roots of the Transcendental Equations Associated with Certain Difference-Differential Equation. Journal of London Mathematical Society, 25, 226-232. http://dx.doi.org/10.1112/jlms/s1-25.3.226
- Matsumoto, A. and Szidarovszky, F. (2013) An Elementary Study of a Class of Dynamic System with Single Time Delay. CUBO A Mathematical Journal, 15, 1-7.
- Farebrother, R.W. (1973) Simplified Samuelson Conditions for Cubic and Quartic Equations. The Manchester School of Economic and Social Studies, 41, 396-406. http://dx.doi.org/10.1111/j.1467-9957.1973.tb00090.x
NOTES

1Linear functions are assumed only for the sake of simplicity. We can obtain a similar learning process to be defined even if both functions are nonlinear. It is also assumed for the sake of simplicity that the firm has perfect knowledge of production technology (i.e., cost function).

2A sailent feature of a discrete-time equation is that the equation involves at least one difference or time-delay of the dependent variable. So we refere to the 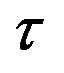 -step delay when
-step delay when 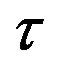 is greater than unity.
is greater than unity.

3With Mathematica, it can be found that the critical value has the following form,
 .
.
4The forms of both conditions are found in Gandolfo . In either from, the stability condition becomes complicated as the order of the equation increases.

