Journal of Mathematical Finance
Vol.06 No.05(2016), Article ID:72038,17 pages
10.4236/jmf.2016.65050
A New Fama-French 5-Factor Model Based on SSAEPD Error and GARCH-Type Volatility
Wentao Zhou1, Liuling Li2
1School of Finance, Nankai University, Tianjin, China
2School of Economics, Nankai University, Tianjin, China
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 30, 2016; Accepted: November 13, 2016; Published: November 16, 2016
ABSTRACT
In this paper, we extend the 5-factor model in Fama and French (2015) with the non-Normal errors distribution of SSAEPD (Standardized Standard Asymmetric Exponential Power Distribution) in Zhu and Zinde-Walsh (2009) and the GARCH- type volatility. The focus is on finding out whether our new model can outperform the original Fama-French 5-factor model. We use Fama-French 25 value-weighted portfolios to conduct our research. The MLE is used to estimate the parameters. The LR test and KS test are used for model diagnostics. Models are compared by AIC. Empirical results show that with GARCH-type volatilities and non-normal errors, the Fama-French 5 factors are still alive. Our new model can successfully capture the skewness, fat-tailness and asymmetric kurtosis in the data and has better in-sample fit than the 5-factors model in Fama and French (2015). Our study provides an update to existing asset pricing literature and reference for investors.
Keywords:
Fama-French 5-Factor Model (FF5), Standardized Standard Asymmetric Exponential Power Distribution (SSAEPD), GARCH, Asset Pricing

1. Introduction
The capital asset pricing model of Sharpe and Lintner (1965) marks the birth of asset pricing theory [1] , which discovers that there exists a positive linear relation between expected returns and their market betas. Three decades later, Fama and French (1993) proposed a three-factor model relating to market premium, Size, B/M and confirmed that the 3-factor model outperformed the single-factor CAPM. [2]
However, recent studies have discovered that many other important patterns in average returns are left unexplained by the 3-factor model. Panel A of Table 1 documents
Table 1. Researches about factor model for stock market.
the development of the factor model in stock market. For example, Carhart (1997) incorporates momentum factor into the Fama-French 3-factor (FF3) model and establishes a Carhart 4-factor (C4) model which documents that stocks performing the best in the short run tend to continue this trend [3] . Chan and Faff (2005) construct a liquidity-augmented FF3 model [4] . Connor, Hagmann and Linton (2012) consider a five-factor extension of the C4 model which suggests an own-volatility factor [5] . Xiao, Faff, Gharghori and Min (2012) incorporate a sustainability factor into 3-factor model which explains the sustainability of the world price better [6] .
In 2015, Fama and French proposed a 5-factor model directed at capturing the size, value, profitability and investment patterns in average stock returns and found it performed better than their 3-factor model [7] . Since then, many studies focusing on Fama-French 5-factor (FF5) model have been done. Panel B of Table 1 presents the researches for the FF5 model. These researches are focused on empirical analysis of FF5 model in different stock markets and comparison between the FF5 model and other models. For example, Hou, Xue and Zhang (2015) find that the 4-factor q-model performs better than the FF5 model in US market [8] . Harshita, Singh, S. and Yadav, S. S. (2015) discover that the FF5 model works better in India than CAPM and FF3 model [9] .
Different from previous researches, our research tries to extend the 5-factor model in Fama and French (2015). Many asset pricing models in the existing literature just assume that financial time series follow the normal distribution, but more and more researches and studies have observed the unique distributional properties of financial data―more kurtosis and higher peak―contradicting the assumption of normality [10] . Thus, instead of adding new factors, we incorporate the GARCH-type volatilities of Bollerslev (1986) into FF5 model and employ non-normal errors of SSAEPD proposed by Zhu and Zinde-Walsh (2009) for the error term. SSAEPD is capable of capturing many stylized facts in financial time series such as skewness, fat tails and asymmetric kurtosis [11] . We denote our new model as FF5-SSAEPD-GARCH. Based on our new model, we try to figure out the following two questions:
1) With GARCH-type volatilities and SSAEPD errors, are the Fama-French 5 factors still alive?
2) Can our new model beat the 5 factor model in Fama and French (2015)?
To answer these questions, we first run simulation to test whether the MatLab program we write can be used in our analysis. Then, Fama-French 25 value-weighted port- folios are analyzed. Data are downloaded from the French’s Data Library, and the sample period is from Jul. 1963 to Dec. 2013. Method of Maximum Likelihood Estimation (MLE) is used to estimate the parameters. Likelihood Ratio test (LR) and Kolmogorov- Smirnov test (KS) are exploited for model diagnostics. Akaike Information Criterion (AIC) is employed for model comparison.
Simulation results show our MatLab program can be employed for our empirical analysis. According to the empirical results, we find out the 5 factors in Fama and French (2015) are still alive! The new model fits the data well and has better in-sample fit than the 5-factor model in Fama and French (2015).
The paper proceeds as follows. The model and methodology are discussed in Section 2. Simulation analysis is reported in Section 3. Empirical results and the model comparisons are presented in Section 4. Section 5 provides the conclusions and future extensions.
2. Model and Methodology
2.1. Fama-French 5-Factor Model (FF5-Normal)
Fama and French (2015) propose a 5-factor model (denoted as FF5) to capture the size, value, profitability, and investment patterns in expected stock returns, and show this model empirically outperforms their 3 factor model. The 5-factor model is:
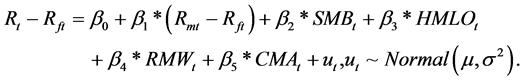 (1)
(1)
where θ = (β0, β1, β2, β3, β4, β5, μ, σ) are parameters to be estimated in this model. 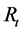 is the return on stock portfolio for period t. Rft is the risk-free return. Rmt is the value-weighted market return. SMBt is the return on small stock portfolio minus the return on big stock portfolio. HMLOt is the high book-to-market ratio minus low book-to-market ratio orthogonalized1. RMWt stands for robust operating profitability portfolios minus weak operating profitability portfolios. CMAt stands for conservative investment portfolios minus aggressive investment portfolios. The error term
is the return on stock portfolio for period t. Rft is the risk-free return. Rmt is the value-weighted market return. SMBt is the return on small stock portfolio minus the return on big stock portfolio. HMLOt is the high book-to-market ratio minus low book-to-market ratio orthogonalized1. RMWt stands for robust operating profitability portfolios minus weak operating profitability portfolios. CMAt stands for conservative investment portfolios minus aggressive investment portfolios. The error term  is distributed as the Normal.
is distributed as the Normal.
2.2. The FF5-SSAEPD-GARCH Model
Based on the GARCH-type volatility in Bollerslev (1986) and non-Normal error distribution of SSAEPD in Zhu and Zinde-Walsh (2009), we extend Fama-French (2015) five-factor model in this section. The new model is denoted as FF5-SSAEPD-GARCH and its math formula is:
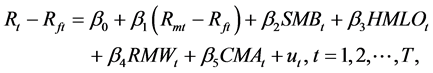 (2)
(2)
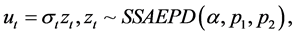 (3)
(3)
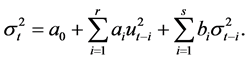 (4)
(4)
where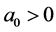 ,
, 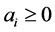 ,
, 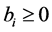 ,
,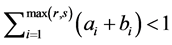 .
.
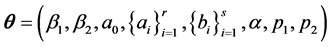 are the parameter vectors to be estimated. T is the sample size. The error term
are the parameter vectors to be estimated. T is the sample size. The error term 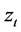 is distributed as the Standardized Standard Asymmetric Exponential Power Distribution (SSAEPD) proposed by Zhu and Zinde-Walsh (2009).
is distributed as the Standardized Standard Asymmetric Exponential Power Distribution (SSAEPD) proposed by Zhu and Zinde-Walsh (2009). 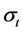 is the conditional standard deviation, i.e., volatility. With
is the conditional standard deviation, i.e., volatility. With ,
, 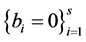 ,
,  ,
, 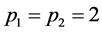 , the FF5-SSAEPD-GARCH model reduces to the FF5-Normal model.
, the FF5-SSAEPD-GARCH model reduces to the FF5-Normal model.
・ Standardized Standard AEPD (SSAEPD)
The probability density function (PDF) of the SSAEPD proposed by Zhu and Zinde- Walsh (2009) is

where






And


2.3. Maximum Likelihood Estimation
In this paper, we estimate the FF5-SSAEPD-GARCH model with Maximum Likelihood Estimation (MLE). The likelihood function is

where



3. Simulation Analysis
In this section, we first generate random number series for




We choose 
1) Given α = 0.5, p1 = p2 = 2, we can generate SSAEPD random number series
2) Set the initial value



3) Generate random number series
4) Set β0 = 0.2, β1 = 1, β2 = 0.5, β3 = 0.5, β4 = 0.5, β5 = 0.5 and we can get
After getting the simulated data

4. Empirical Analysis
4.1. Data
The data we analyze are the monthly returns from the Fama-French 25 value-weighted portfolios for US stock market, which are the same as data used in Fama and French (2015). The descriptive statistics of sample data are calculated by MatLab and listed in Table 3. For each observation, the skewness estimates (except one case) is not 0 and all kurtosis estimates are more than 3, which suggests that the data follows a leptokurtic distribution with the high peak and fat tail. The P-value of Jarque-Bera test for each portfolio is 0, which is smaller than 5% significance level. Hence, we can reject the null hypothesis and conclude that the asset returns do not follow Normal distribution. Thus, non-Normal error of SSAEPD might be able to fit the data better.
Table 2. Simulation results.
Notes: T means the true value of parameters. E means the estimates. P means the error in percentage.
Table 3. Descriptive statistics (1963:7 - 2013:12).
4.2. Estimation Results
Estimates for the FF5-SSAEPD-GARCH Model
The estimates for our new model are displayed in Table 4. We find out that our model can successfully capture the skewness, fat-tailness and asymmetric kurtosis of the data. To be specific, the skewness parameters α are all not equal to 0.5, which captures the skewness in the data. 44 out of 50 estimates for the tail parameters pi (i = 1, 2) are smaller than 2, which suggests that portfolio returns are fat-tailed distributed. Besides, all the tail parameters p1 and p2 are not equal to each other, which document the asymmetric kurtosis. And 15 out of 25 portfolios have bigger estimates for the left tail parameter p1, which means that these returns have thinner left tails.
Table 4. Estimates on FF5-SSAEPD-GARCH (Monthly, 1963:07 - 2013:12).
4.3. Model Diagnostics
To test the significance of coefficients in our new model, Likelihood Ratio test (LR) is applied, LR formula is from Neyman and Pearson (1993), which is Equation (18).

4.3.1. Tests for Parameter Restrictions
・ Tests for Parameters in the Mean Equation
The P-values of LR are listed in Table 5. The null hypothesis of the joint significance test is H0: β1 = β2 = β3 = β4 = β5 = 0. The P-values of the joint significance test for all the 25 portfolios are 0, which means β1, β2, β3, β4 and β5 are statistically jointly significant under 5% significance level. The individual significance tests show that under 5% significance level the coefficient β1 in all 25 portfolios are statistically significant; 24/25 portfolios have a statistically coefficient β2 and β5; 23/25 and 19/25 portfolios have a statistically coefficient β3 and β4, respectively. As for coefficient β0, 16 out of the 25 portfolios don’t have a statistically significant coefficient β0 under 5% significance level. Thus, we can conclude that with non-Normal errors such as SSAEPD and GARCH- type volatilities, the Fama-French 5-factor model is still alive.
・ Tests for Parameters in the GARCH Equation
In this part, some restrictions on the parameters in the GARCH equation are tested with Likelihood Ratio test (LR). And the results are listed in Table 5. Results show the GARCH-type volatility should be included in Fama-French 5 factor model. For instance, we do the joint significance test for hypothesis H0: b = c = 0. The P-values of the LR are all smaller than the significance level 5%, which means our GARCH-type volatility is quite necessary. As for individual hypotheses, we discover that most P-values of LR are smaller than the significance level 5%. And to be specific, ARCH term (H0: b = 0) is significant in 20 out of 25 portfolios and GARCH term (H0: c = 0) is significant in 18 out of 25 portfolios.
・ Tests for Parameters in SSAEPD
We also run significance tests for the parameters in the SSAEPD and the results of parameter restrictions show strong non-Normality. And the results are listed in Table 5. For example, for the Hypothesis H0: α = 0.5, p1 = p2 = 2, 21 out of 25 p-values are smaller than the significance level 5%, which means that Normal error assumption is not supported by most of our data. Besides, Asymmetry is documented (H0: α = 0.5 is rejected by 7 out of 25 portfolios). And non-normality is found (H0: p1 = 2 is rejected by 8 out of 25 portfolios and 12 out of 25 portfolios reject the null H0: p1 = 2.).
4.3.2. Residual Check
In this subsection, the residuals for previous models are checked with both Kolmogorov-Smirnov test and graphs. Our results show that 20 out of the 25 portfolios have residuals which do follow SSAEPD. That means our new model is adequate for the Fama- French 25 portfolios. But the FF5-Normal model is not adequate for the data, since 21 portfolios have residuals which do not follow the Normal error distribution.
Table 5. P-values of likelihood ratio test (LR).
Note: * means the null is rejected under 5% significant level.
・ Kolmogorov-Smirnov Test for Residuals
To check the residuals, the Kolmogorov-Smirov test (KS) is employed. The P-value of KS test is displayed in Table 6. The P-values of KS test show the residuals from the new model do follow SSAEPD. For example, the P-value of the portfolio with Small Size and Low Book-to-market is 0.71, greater than 5%, which means under 5% significance level, the null hypothesis is not rejected and the residuals from our model do follow the SSAEPD. Similarly, the null hypothesis cannot be rejected for other 19 portfolios.
Then, we apply the KS test for the residuals from the FF5-Normal model. The P-values of the KS test are also listed in Table 6. 21 out of 25 portfolios have smaller P-values than 0.05, which means these 21 portfolios reject the nulls. Hence, the error terms of the portfolios do not follow Normal distribution. And the FF-Normal model is not adequate for the data.
・ PDFs of Residuals
By method of “eye-rolling”, the PDF of residuals is compared with theoretical PDFs. Taking the portfolio with Small Size and Low Book-to-market for example, in Figure 1, the probability density function (PDF) for the estimated residuals 

Similarly, the probability density function (PDF) for the estimated residuals 

4.4. Model Diagnostics
In this subsection, we compare our new model with the 5-factor model of Fama and French (2015). The Akaike Information Criterion (AIC) is used as the model selection criterion. Table 7 displays the AIC values. We find that 23 out of 25 AIC values of the
Table 6. P-values of KS test for residuals.
a. The null hypothesis H0 is: FF5-SSAEPD-GARCH residuals are distributed as

Figure 1. PDFs of the residuals (FF5-SSAEPD-GARCH) and
Figure 2. PDFs of the residuals (FF5-Normal) and
Table 7. AIC values (Monthly, 1963:07 - 2013:12).
Note: Numbers with * are smaller AIC values.
FF5-SSAEPD-GARCH model are smaller than those of the FF5-Normal model. Hence, we can conclude that our new model (FF5-SSAEPD-GARCH) performs better than the 5-factor model in Fama and French (2015).
5. Conclusions
In this paper, we extend the 5-factor model in Fama and French (2015) by introducing a non-normal error term and time-varying volatilities. The non-normal error assumption we used is the SSAEPD in Zhu and Zinde-Walsh (2009). And the time-varying volatilities are the GARCH model in Bollerslev (1986). For comparison, monthly US stock returns in Fama and French (2015) (1963:07 - 2013:12) are analyzed. Method of Maximum Likelihood is used. Likelihood Ratio Test (LR) is used to test the hypotheses of parameter restrictions. Kolmogorov-Smirnov test (KS) is used to check residuals. Akaike Information Criterion (AIC) is used to compare models.
Simulation results show our MatLab program for the new model is valid. And empirical results show: 1) this new model can capture the skewness, fat tails and asymmetric kurtosis in the data; 2) With GARCH-type volatilities and non-normal errors, the Fama-French 5 factors are still alive, since the estimates are all significant; and 3) our new model can fit the data much better than 5-factor model in Fama and French (2015). Our study provides an update to existing asset pricing literature and reference for investors.
Future extensions will include but not limited to the following. First, we can exam our results with different data. Second, we can compare our results with those from other models such as ARIMA model. Last but not the least, other factors can be introduced into this model.
Acknowledgements
We also want to thank participants in the 16th World Business Research Conference at San Francisco (28 - 29 July, 2016) and the seminars organized by Institute of Statistics and Econometrics, Nankai University. The support of Jiayi Zhu and Qingyu Zhu is gratefully acknowledged. The authors are responsible for all errors.
Cite this paper
Zhou, W.T. and Li, L.L. (2016) A New Fama-French 5- Factor Model Based on SSAEPD Error and GARCH-Type Volatility. Journal of Mathematical Finance, 6, 711-727. http://dx.doi.org/10.4236/jmf.2016.65050
References
- 1. Sharpe, W.F. (1964) Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk. Journal of Finance, 19, 425-442.
- 2. Fama, E. and French, K. (1993) Common Risk Factors in the Returns on Stocks and Bonds. Journal of Financial Economics, 33, 3-56.
http://dx.doi.org/10.1016/0304-405X(93)90023-5 - 3. Carhart, M.M. (1997) On Persistence in Mutual Fund Performance. Journal of Finance, 52, 57-82.
http://dx.doi.org/10.1111/j.1540-6261.1997.tb03808.x - 4. Chan, H.W. and Faff, R.W. (2005) Asset Pricing and the Illiquidity Premium. Financial Review, 40, 429-458.
http://dx.doi.org/10.1111/j.1540-6288.2005.00118.x - 5. Connor, G., Hagmann, M. and Linton, O. (2007) Efficient Semiparametric Estimation of the Fama-French Model and Extensions. Econometrica, 80, 713-754.
- 6. Xiao, Y., Faff, R., Gharghori, P. and Min, B.K. (2013) Pricing Innovations in Consumption Growth: A Re-Evaluation of the Recursive Utility Model. Journal of Banking & Finance, 37, 4465-4475.
http://dx.doi.org/10.1016/j.jbankfin.2012.08.015 - 7. Fama, E.F. and French, K.R. (2015) A Five-Factor Asset Pricing Model. Journal of Financial Economics, 116, 1-22.
http://dx.doi.org/10.1016/j.jfineco.2014.10.010 - 8. Hou, K., Xue, C. and Zhang, L. (2015) Editor’s Choice Digesting Anomalies: An Investment Approach. Review of Financial Studies, 28, 650-705.
http://dx.doi.org/10.1093/rfs/hhu068 - 9. Harshita, Singh, S. and Yadav, S.S. (2015) Indian Stock Market and the Asset Pricing Models. Procedia Economics & Finance, 30, 294-304.
http://dx.doi.org/10.1016/S2212-5671(15)01297-6 - 10. Malmsten, H. and Svirta, T. (2011) Stylized Facts of Financial Time Series and Three Popular Models of Volatility. European Journal of Pure & Applied Mathematics, 3, 443-477.
- 11. Zhu, D.M. and Zinde-Walsh, V. (2009) Properties and Estimation of Asymmetric Exponential Power Distribution. Journal of Econometrics, 148, 86-99.
http://dx.doi.org/10.1016/j.jeconom.2008.09.038
Appendix 1. Estimates for the FF5-Normal Model
To test our MatLab program, we also estimate the FF5-Normal model using the program by setting

Table 8. Estimates for FF5-normal model by our MatLab program (Monthly, 1963:07 - 2013:12).
Table 9. Estimates in Fama and French (2015) (Monthly, 1963:07 - 2013:12).
Note: This table is quoted from the results in Table 7 on page 13 of Fama and French (2015).







