ABSTRACT

This paper analyses the Gerber-Shiu penalty function of a Markov modulated risk model with delayed by-claims and random incomes. It is assumed that each main claim will also generate a by-claim and the occurrence of the by-claim may be delayed depending on associated main claim amount. We derive the system of integral equations satisfied by the penalty function of the model. Further, assuming that the premium size is exponentially distributed, an explicit expression for the Laplace transform of the expected discounted penalty function is derived. For a two-state model with exponential claim sizes, we present the explicit formula for the probability of ruin. Finally we numerically illustrate the influence of the initial capital on the ruin probabilities of the risk model using a specific example. An example for the risk model without any external environment is also provided with numerical results.

Keywords:

Gerber-Shiu Penalty Function, Markov Modulated Risk Model, Random İncome, Delayed Claims

1. Introduction

Analyzing a risk model using the Gerber-Shiu discounted function largely promoted the theory and provided a useful tool for the computation of many performance measures. As a classical risk model is too idealistic, in fact there are a lot of distracters, it has become necessary to study risk models having parameters governed by the external environment. Recently many authors considered risk models having Markov modulated environment or Markovian regime-switching models. The purpose of this generalization is to enhance the flexibility of the model parameters for the classical risk process. For a Markov modulated Poisson process, the arrival rate varies according to a given Markov process. The risk models managed by an insurance company are a long-term program and system parameters such as interest rates, premium rates, claim arrival rates, etc. may need to change whenever economic or political environment changes. So it is always preferable to regulate the model according to the external environment.

The assumption on independence among claims is an important condition used in the study of risk models. However, in many practical situations, this assumption is inconsistent with the operation of insurance companies. In reality, claims may be time- correlated for various reasons, and it is important to study risk models which can also depict this phenomenon. Two types of individual claims, main claims and associated by-claims are introduced, where every by-claim is induced by the main claim and could be delayed for one time period depending on the amount to be paid towards the main claim. Further, we discuss the model in the presence of random incomes in order to accommodate insurance companies having lump sums of income occurring time to time based on their business and other related activities.

The idea of delayed claims is gaining importance due to its relevance in many real world situations. Xie et al. [1] considered the expected discounted penalty function of a compound Poisson risk model with delayed claims and proved that the ruin probability for the risk model decreases as the probability of the delay of by-claims is increasing, while in [2] the authors discussed the model perturbed by diffusion. The same authors in [3] presented an explicit formula for the ruin probability when the claims were delayed. Delayed claim risk models were first introduced by Waters et al. [4] so that the independence assumption between claim sizes and their interarrival times can be relaxed and since then it has been investigated by many researchers. Hao et al. [5] analyzed the risk model with delayed claims in a financial market where the probability of delay of each claim is constant and independent of claim amounts.

Yu [6] studied the expected discounted penalty function in a Markov Regime- Switching risk model with random income. Assuming that the premium process is a Poisson process, Bao [7] obtained the Gerber-Shiu function of the compound Poisson risk model. In this paper the author discussed the ruin model in which the premium is no longer a linear function of time but a Poisson process. Zhu et al. [8] considered the expected discounted penalty function of a compound Poisson risk model with random incomes and potentially delayed claims. Huang and Yu [9] investigated the Gerber-Shiu discounted penalty of a Sparre-Andersen risk model with a constant dividend barrier in which the claim inter-arrival distribution is the mixture of an exponential distribution and an Erlang (n) distribution.

J. Gao and L. Wu [10] considered a risk model with random income and two types of delayed claims and derived the Gerber-Shiu discounted penalty function using an auxiliary risk model. This was done as an extension of the work by Xie et al. in [1] and [2] . More developments about compound Poisson models can be found in Hao and Yang [11] where they analyze the expected discounted penalty function of a compound Poisson risk model with random incomes and delayed claims. In this paper, we investigate a general form of such a risk model by assuming the existence of Markovian environment.

The rest of this paper is organized as follows. In Section 2, we describe the risk model considered. In Section 3, the integral equations for the expected discounted penalty function are obtained. Section 4 deals with the case with exponential random incomes and Laplace transforms of the discounted penalty function derived. In Section 5, we illustrate the usefulness of the model by computing probability of ruin for a model having only two states and in Section 6 a risk model without any external environment. Section 7 concludes the paper.

2. The Risk Model

Here we consider a continuous time risk model with random incomes, two types of insurance claims, namely the main claims and the by-claims, and where the parameters are depending on the external environment. Let 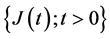be the external environment process which is assumed to be a homogenous irreducible and recurrent continuous time Markov chain with finite state space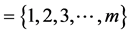, intensity matrix

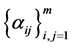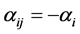and for.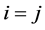

Let and 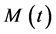be respectively, the number of claims and the random incomes occurring in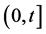. Let be the epoch of the nth claim and 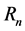be the epoch of the nth random premium. When 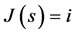for all s in a small interval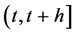, the number of claims occurring in that interval is assumed to follow the Poisson distribution with parameter 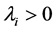and the nth main claim amount 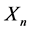has the distribution function, density function 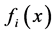and finite mean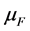. Also the number of random premiums follows the Poisson distribution with parameter 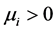and the nth premium amount having the distribution, density function and finite mean. Each main claim will generate a by-claim and when, let be the distribution function of the by-claim amount, the density function and the finite mean. These, and are assumed to be iid positive random variables and are independent of each other. Moreover, the processes; and have independent increments.

The processes and are Markov-modulated Poisson processes, which are special cases of the Markovian Arrival Process (MAP). The claim arrival rates, claim amounts, income arrival rates and random incomes are all driven by the external environment process.

In this paper, we consider the risk model having the following claim occurrence process. There will be a main claim at every epoch of the Poisson process and this will induce a by-claim . Moreover if the main claim amount is less than the threshold level, then both the main claim and associated by-claim occurs simultaneously. If the main claim amount is larger than or equal to the threshold, then the occurrence of the by-claim is delayed to the next claim epoch. If the occurrence of the by-claim is delayed to, then the delayed claim and the main claim occur simultaneously.

In this set up, the surplus process of the risk model is defined as

(1)

where u is the initial capital and is the sum of all by-claims that occurred upto time t. Define the time of ruin by. The ruin probabilities given initial capital u are . Let and be the surplus immediately before ruin and the deficit at ruin respectively. The Gerber- Shui discounted penalty function is of the form

where is the discounted factor, is the penalty function and is the indicator function of the event A.

The safety loading condition is

Now let us consider an auxiliary risk model, which is same as the one described above with a slight change assumed at the first claim epoch. Instead of having one main claim and a by-claim with probability at the first epoch, we have another by-claim Y added at the first epoch. i.e.; by-claim Y and the main claim occur at simultaneously. Hence the corresponding surplus process of this auxiliary risk model is defined as

(2)

where Y denotes the other by-claim amount added at the first claim epoch and let. Assume that Y and are iid positive random variables. Let denote the Gerber-Shiu discounted penalty function that can be defined for the auxiliary model corresponding to the initial environment.

3. System of Integral Equations

We are interested in the Gerber-Shiu discounted penalty function of the model. Analyzing the surplus process in a small interval, for, we have the following cases:

1) During no claim occurs, no premium arrivals and no change in the external environment.

2) During the time interval, one main claim and a by-claim occurs, main claim is less than the threshold level, no premium arrival and no change in the external environment.

3) One main claim and a by-claim occurs in, main claim is more than the threshold level (this transfers by-claim amount to the next claim point), no premium arrival and no change in the external environment.

4) No claim occurs in but one premium arrival and no change in the external environment.

5) No claim occurs, no premium arrival in but a change in the external environment in.

6) All other events having total probability.

The Gerber-Shiu discounted penalty function of the model satisfies equation,

(3)

Similarly, for the auxiliary model we have

(4)

Expanding, dividing by t and taking as limit in (3) and (4) we get,

(5)

(6)

Substituting,

,

and;

in the Equations (5) and (6). They reduce to,

(7)

For the auxiliary model, it is

(8)

where,

and

.

Remark 1: Letting and, above expressions will give the Laplace transform of time to ruin.

Remark 2: Letting and, the ruin probabilities for the model is obtained.

Remark 3: Letting, we get the discounted expectation of the deficit at ruin for the model.

4. Laplace Transform of Gerber-Shiu Function for the Model with Exponential Incomes

This section assumes that the random premium amounts are exponentially distributed and we derive the Laplace transform of the Gerber-Shiu function.

Writing as the Laplace transform of,

i.e.

we have,

(9)

where

,

and

Similarly for the auxiliary model we have,

(10)

where

and

.

Suppose that the random income are exponentially distributed (i.e.) .

Then we have,

Hence,

and

Further simplifying we have,

(11)

and

(12)

5. Explicit Results for a Two-State Model with Exponential Claims and Degenerate Threshold

We consider the case where all the by-claims are delayed to the next claim epoch and both claim amounts are exponentially distributed, i.e.; the distribution functions are

and. Also let (only two external environment states).

The probability of ruin is obtained by putting in Equations (11) and (12).

We have,

;;;;

;;;;.

(13)

(14)

(15)

. (16)

Numerical example 1: Let;;;;;; ;;;;.

Then we have. Table 1 shows the ruin probabilities of the example and further Figure 1 and Figure 2 show the ruin probabilities for different values of u.

One can note from the graph that in Figure 1, and decrease sharply when u is in and then turns flat as u increases. The same observation is made in Figure 2 for and.

6. Explicit Results for the Model with Exponential Claims and No External Environment

In this section, we consider the risk model without external environment (i.e.; and all the other assumptions remaining the same as in Section 5. Resulting equations for the ruin probabilities are,

(17)

(18)

where.

Numerical example 2: Let. From Table 2, we can see the behavior of ruin probabilities in this model.

Figure 3 shows the ruin probabilities in Example 2 for different values of u. One can see that, and decreases sharply when u is in and then turn flat when u increases further.

7. Conclusions

In this paper, we investigated a Markov-modulated risk model with random incomes

and two types of claims (i.e., main claims and by-claims) and where the by-claims may be delayed to the next claim point. We assume that the by-claim can be delayed depending on the corresponding main claim amount; whether it is exceeding the random threshold. All system parameters are assumed to be depending on the state of the external environment. System of integral equations for the Gerber-Shiu penalty function was obtained. Then we obtained Laplace transforms of the penalty function under the assumption that the random incomes follow an exponential distribution. Next for a simplified model with exponential claim amounts, we presented expressions for the probability of ruin and some numerical illustrations included. Finally we considered another simplified model in the absence of external environment and numerically illustrated the influence of initial capital on the ruin probabilities.

Future research includes investigation of the risk model with generalized distributions. It would be also interesting to find other ruin related parameters like surplus prior to ruin, deficit at ruin, etc.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Cite this paper

Shija, G. and Jacob, M.J. (2016) Gerber Shiu Function of Markov Modulated Delayed By-Claim Type Risk Model with Random Incomes. Journal of Mathematical Finance, 6, 489-501. http://dx.doi.org/10.4236/jmf.2016.64039

References