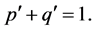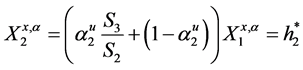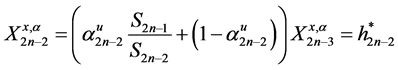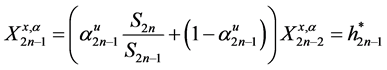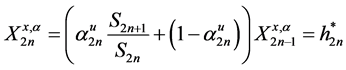Journal of Mathematical Finance
Vol.06 No.02(2016), Article ID:66409,6 pages
10.4236/jmf.2016.62023
Measure of Investment Optimal Strategy
J. T. Eghwerido*, E. Ekuma-Okereke, E. Efe-Eyefia, Edwin Iguodala, T. O. Obilade
Department of Mathematics and Computer Science, Federal University of Petroleum Resources Effurun, Nigeria

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 January 2016; accepted 9 May 2016; published 12 May 2016
ABSTRACT
In this paper, we considered the different strategies that generate the optimal wealth on investment. The strategy examine depends on the utility function an investor is willing to adopt, say H* at time N in every 2n possible states; in an N period setting. Negative exponential, logarithm, square root and power utility functions were established, as the market structures changed according to a Markov chain through a martingale approach. The problem of maximization is solved via Lagrange method. The performance of the investment from day-to-day is driven by the ratio of the risk neutral probability and the probability of rising to falling.
Keywords:
Martingale, Negative Exponential, Logarithm, Square-Root, Power Utility Functions

1. Introduction
Portfolio management is a fundamental aspect in economics and finance. It is an all natural and important activity in our society for households, pension fund managers, as well as for government debt managers. The principle covers numerous and various situations of daily life. In a financial terminology, the problem of portfolio optimization of an investor trading in different assets is to choose an optimal strategy for an investment. This involves how many shares of which asset he should hold at any trading time, in order to maximize some subjective (depending on his preferences) criterion relying on his total wealth and/or consumption which in turn depends on the prices. Portfolio management is all about strengths, weaknesses, opportunities and threats in the choice of debt versus equity, domestic versus international, growth versus safety, and other trade-offs en- countered at the attempt to maximize return at a given appetite for risk. Investors need to balance the objective of maximizing the return of their investment with the constraint of minimizing the risk involved. It is generally accepted that the greater the expected return is, the greater the risk involved is.
Portfolio management (PM) guides the investor in a method of selecting the best available securities that will provide the expected rate of return for any given degree of risk and also to mitigate (reduce) the risks. Prices of assets depend crucially on their risk as investors typically demand more profit for bearing more uncertainty. Therefore, today’s price of a claim on a risky amount realized tomorrow will generally differ from its expected value. Most commonly, investors are risk-averse and today’s price is below the expectation, remunerating those who bear the risk.
Due to the high liquidity, leverage effects and their non-linear pay-off profile, together with options and other derivatives are now widely used as an investment opportunity. However, a straight forward generalization of the stochastic control approach leads to a much more complicated form of the Hamilton Jacobi Bellman equations (HJB-equations). Thus, the martingale approach of portfolio optimization deals with this problem. Hence, for any investment we have,
 (1)
(1)
where;
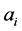 = amount invested in security i.
= amount invested in security i.
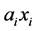 = investment returns.
= investment returns.
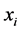 = a non-negative random variable.
= a non-negative random variable.
 = the rate of return from investment i.
= the rate of return from investment i.
With payment  returns an amount
returns an amount 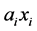 after one period. The rate of return is that value
after one period. The rate of return is that value 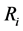 that makes the present value of the return equal to the initial payment.
that makes the present value of the return equal to the initial payment.
The traditional technique for solving dynamic programming [DP] problem stated suffers from the so-called curse of dimensionality. That is, the computational requirements of a dynamic programming problem [that needs to be solved numerically] grow exponentially in the dimensionality of the problem. One technique that applies to solving portfolio optimization problems in complete markets, is the Martingale method.
The idea behind this method is very simple: since markets can be assumed to be stable and complete, in the sense that there is no fluctuation, every contingent claim is attainable and therefore the initial price of any random variable representing a contingent claim can be computed.
In financial market where investors are facing uncertainty, the strategy that optimizes the return of an invest- ment in assets is in general not known. Suppose that the investor compares random returns whom he knowns the
probability distributions on some probability space , hence, a portfolio manager maximizes the
, hence, a portfolio manager maximizes the
expected utility of his terminal wealth in a complete market with a stochastic interest rate [1] , which follows the affine dynamics [2] that allows partial risk transfer between the contributor and the fund manager [3] . L. Delong et al. [4] stated that such asset allocation strategies will be achieved only in pre-retirement accumulation phase. Thus, the optimal investment strategy follow a composite asymptotic expansion [5] . Furthermore, Eghwerido et al. [6] [7] established a case where we have negative exponential, logarithmic, square root, power utility functions with a returns on investment and their generalized form; while [8] proposed asset allocation for payment of long-term liability in a multi-period discrete time where [9] determined an equilibrium strategies for maximizing exponential utility. Korn [10] emphasized optimal investment. Also, [11] deals with investor which has the opportunity to put her wealth into derivatives with counter party risk or credit derivatives. Korn [12] considered a portfolio process yielding the highest worst-case bound where trading in the risky asset is stopped if a state process hits a predefined barrier [13] hence, mathematical theory of speculative prices through a feed back was developed elaborately [14] [15] .
The mean-variance criterion of Markowitz [16] in a one-period decision model that risk is only measured in terms of the variance of the portfolio return is criticized; that symmetric form of the variance has the undesirable side effect of not only bounding possible losses, but also possible gain [17] . Mulvey et al. [18] state that multi- stage simulation and optimization are effective for solving long-term financial planning problems. Oshorne develops the proposition that it is not absolute price changes but the logarithmic price changes which are independent of each other. [19] [20] emphasized on characterization of optimal control for diffusion processes; while Roger considered a case where an investor faced with the classical Merton problem of optimal investment in a log-Brownian asset and a fixed-interest bond, but constrained only to change portfolio. [21] [22] stressed on utility maximization in incomplete markets through semimartingale model for incomplete markets, and to characterize it via the associated dual problem. Schweizer [23] developed area of pricing and hedging contingent claims in an incomplete market by means of a quadratic criterion and [24] showed that they might be represented by an expected utility criterion.
More precisely, by denoting 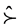 the preference order on the set of random returns, we say that
the preference order on the set of random returns, we say that  satisfies the criterion if and only if there exists some increasing function U from
satisfies the criterion if and only if there exists some increasing function U from 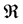 into
into  called utility function, such that
called utility function, such that
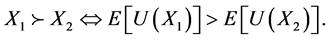 (2)
(2)
The increasing property of the utility functions means that the investor prefers more wealth. Thus, the choice of the utility function allows investor the notions of risk aversion and risk premium related uncertainty, hence the strategy that delivers the optimal terminal wealth.
2. Optimal Returns with Different Utility Functions
In a financial market where investors are facing uncertainty, the return of an investment in assets is in general not known. For example, a stock yield depends on the resale price and the dividends. How to choose between several possible investments? In order to determine desirable strategies in an uncertain context, the preferences of the investor should be made explicit, and this is usually done in terms of expected utility criterion.
Negative exponential, Logarithmic, square root, power utility functions returns on investment were es- tablished [6] [7] .
Thus for negative exponential, we have
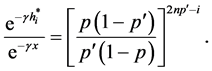
Now, suppose an investor wishes a Logarithmic rate of return, then

A market structure with a square root utility function with even step structure could also be,
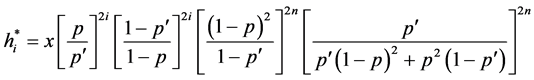
The power utility function is a generalization of the square root utility function. Thus, for an investor with power utility function return we have,
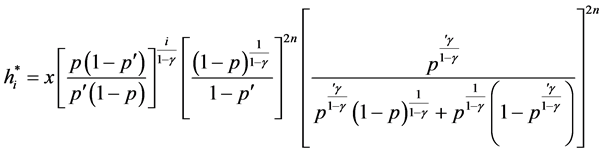
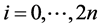

3. Model Formulation
The strategy generating the optimal wealth resulted in the terminal wealth 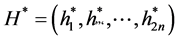
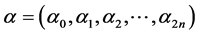

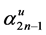
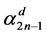

Thus, the wealth value at time t is given by
On and on to
This is some sort of multiplicative effect of the wealth 

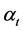
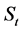
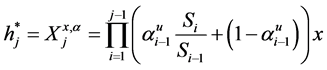
with,

But, terminal wealth must be equivalent to optimal strategy, 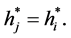
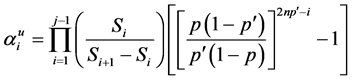
Now, suppose an investor wishes a Logarithmic return on investment, its optimal strategy will be
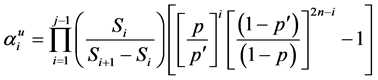
An investor with intension of a less risk investment such as the square root will have

Morealso, for the power model is a generalization of the square root model, thus we have
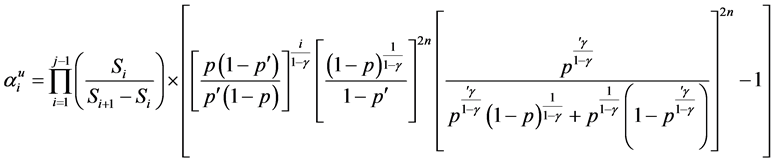
4. Concluding Remarks
This study concludes that the optimal strategy is determined by the ratio 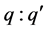
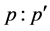
different utility models showed that the Negative exponential utility model gave the best strategy of wealth which of-course, more risky.
Various strategies with different Utility functions were established. The utility functions considered are negative exponential, logarithm, square root and power utility functions. The N-step utility model results show the ratio of the utility functions at time point i in comparison with the initial starting time. The strategy with different utility models depends on the amount of risk an investor is willing to bear at each trading period. The results showed that the Negative exponential utility model gave the best strategy.
In the subsequent paper, the model will be used to predict the performances of some selected companies in the Nigeria Capital Market.
Cite this paper
J. T. Eghwerido,E. Ekuma-Okereke,E. Ekuma-Okereke,E. Efe-Eyefia,Edwin Iguodala,T. O. Obilade, (2016) Measure of Investment Optimal Strategy. Journal of Mathematical Finance,06,269-274. doi: 10.4236/jmf.2016.62023
References
- 1. Battocchio, P. and Menoncin, F. (2004) Optimal Pension Management in a Stochastic Framework. Insurance: Mathematics and Economics, 34, 79-95.
http://dx.doi.org/10.1016/j.insmatheco.2003.11.001 - 2. Deelstra, G., Grasselli, M. and Koehl, P.-F. (2003) Optimal Investment Strategies in the Presence of a Minimum Guarantee. Insurance: Mathematics and Economics, 33, 189-207.
http://dx.doi.org/10.1016/S0167-6687(03)00153-7 - 3. Deelstra, G., Grasselli, M. and Koehl, P.-F. (2004) Optimal Design of the Guarantee for Defined Contribution Funds. Journal of Economic Dynamics and Control, 28, 2239-2260.
http://dx.doi.org/10.1016/j.jedc.2003.10.003 - 4. Delong, L., Gerrard, R. and Haberman, S. (2008) Mean-Variance Optimization Problems for an Accumulation Phase in a Defined Benefit Plan. Insurance: Mathematics and Economics, 42, 107-118.
http://dx.doi.org/10.1016/j.insmatheco.2007.01.005 - 5. Emms, P. and Haberman, S. (2007) Asymptotic and Numerical Analysis of the Optimal Investment Strategy for An Insurer. Insurance: Mathematics and Economics, 40 113-134.
http://dx.doi.org/10.1016/j.insmatheco.2006.03.003 - 6. Eghwerido, J.T. and Obilade, T.O. (2014) Optimization of Investment Returns with N-Step Utility Functions. Journal of the Nigerian Mathematical Society, 33, 311-320.
- 7. Eghwerido, J.T., Efe-Eyefia, E and Ekuma-Okereke, E (2015) Investment Returns with N-Step Generalized Utility Functions. ICASTOR Journal of Mathematical Sciences, 9, 51-55.
- 8. Hong-Chih, H. (2010) Optimal Multiperiod Asset Allocation: Matching Assets to Liabilities in a Discrete Model. Journal of Risk and Insurance, 77, 451-472.
http://dx.doi.org/10.1111/j.1539-6975.2009.01350.x - 9. Korn, R. (2005) Worst-Case Scenario Investment for Insurers. Insurance: Mathematics and Economics, 36, 1-11.
http://dx.doi.org/10.1016/j.insmatheco.2004.10.004 - 10. Korn, R. and Korn E. (2001) Option Pricing and Portfolio Optimization. AMS, Providence.
http://dx.doi.org/10.1007/978-3-322-83210-8 - 11. Korn, R. and Kraft, H. (2003) Optimal Portfolios with Defaultable Securities: A Firms Value Approach. International Journal of Theoretical and Applied Finance, 6, 793-819.
http://dx.doi.org/10.1142/S0219024903002213 - 12. Korn, R. and Menkens, O. (2005) Worst-Case Scenario Portfolio Optimization: A New Stochastic Control Approach. Mathematical Methods of Operations Research, 62, 123-140.
http://dx.doi.org/10.1007/s00186-005-0444-3 - 13. Kraft, H. and Steffensen, M. (2006) Portfolio Problems Stopping at First Hitting Time with Application to Default Risk. Mathematical Methods of Operations Research, 63, 123-150.
http://dx.doi.org/10.1007/s00186-005-0026-4 - 14. Bachelier’s, L. (1990) 'Theory of Speculation. Princeton Press, Princeton.
- 15. MacDonald, B.-J. and Cairns, A.J.G. (2009) Getting Feedback on Defined Contribution Pension Plans. Journal of Risk and Insurance, 76, 385-417.
http://dx.doi.org/10.1111/j.1539-6975.2009.01304.x - 16. Markowitz, H. (2005) Portfolio Selection. Journal of Finance, 7, 77-91, 19.
- 17. Martin, H. (2005) Martingale Pricing Applied to Dynamic Portfolio Optimization and Real Options. International Journal of Theoretical and Applied Finance, 11 p.
- 18. Mulvey, J. andShetty, B. (2004) Financial Planning via Multi-Stage Stochastic Optimization. Computers and Operations Research, 31, 1-20.
http://dx.doi.org/10.1016/S0305-0548(02)00141-7 - 19. Oshorne. The Econometric Modelling of Financial Time Series. 2nd Edition, Terence Mills.
http://www.cambridge.org/ - 20. Pham, H. (2005) On Some Recent Aspects of Stochastic Control and Their Applications. Probability Surveys, 2, 506- 549.
http://dx.doi.org/10.1214/154957805100000195 - 21. Rogers, L.C.G. (2001) The Relaxed Investor and Parameter Uncertainty. Finance Stochastic, 5, 131-154.
http://dx.doi.org/10.1007/PL00013532 - 22. Schachermayer, W. (2003) Utility Maximization in Incomplete Markets. In: Fritelli, M. and Runggladier, W., Eds., Stochastic Methods in Finance, Lectures Given at the CIME-EMS Summer in Bressanone/Brixen, Springer Lecture notes in Mathematics, 1856.
- 23. Schweizer, M. (2001) A Guided Tour through Quadratic Hedging Approaches. In: Jouini, E., Museiela, M., and Cvitanic, J., Eds., Option Pricing Interest Rates, and Risk Management, Cambridge University Press, Cambridge, 538-574.
http://dx.doi.org/10.1017/CBO9780511569708.016 - 24. Von-Neumann and Morgenstern (1947) Theory of Games and Economic Behavior. Princeton University Press, Princeton.
http://press.princeton.edu/chapters/i7802.pdf.1947
NOTES
*Corresponding author.