Journal of Mathematical Finance
Vol.05 No.05(2015), Article ID:61562,9 pages
10.4236/jmf.2015.55038
State Price Density Estimation and Nonparametric Pricing of Basket Options
Yuming Kuang, Tze Leung Lai
Department of Statistics, Stanford University, Stanford, CA, USA

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 2 October 2015; accepted 27 November 2015; published 30 November 2015

ABSTRACT
This paper develops a novel method to price basket options by using an application-driven approach to estimating the state price density of the basket or the joint state price density of the asset prices in the basket. In this connection, we also discuss the difference between the application-driven and the traditional statistical approach to density estimation.
Keywords:
Basket Options, Portfolio Weights, Joint State Price Density

1. Introduction
Basket options are popular derivative contracts. A basket option is an option whose payoff depends on the value of a portfolio (or basket) of n assets which are usually individual stocks or stock indices, currencies or commodities. The value of the portfolio at some future time T is  in which
in which 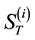 is the price of the ith asset and the
is the price of the ith asset and the 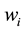 is the portfolio weights (possibly negative). Therefore the price of a European call option on the basket, with maturity T and strike price X, is
is the portfolio weights (possibly negative). Therefore the price of a European call option on the basket, with maturity T and strike price X, is
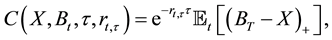 (1)
(1)
in which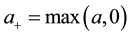 ,
, 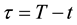 ,
,  denotes conditional expectation, under the risk-neutral measure, given the information set (or more precisely the
denotes conditional expectation, under the risk-neutral measure, given the information set (or more precisely the 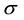 -field of events) up to time t, and
-field of events) up to time t, and  is the interest rate of a risk-free bond, with maturity
is the interest rate of a risk-free bond, with maturity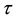 , at current time t. Even under the usual assumption that the asset prices
, at current time t. Even under the usual assumption that the asset prices 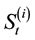 follow correlated geometric Brownian motion processes, the computation of (1) involves Monte Carlo simulations, unlike the case
follow correlated geometric Brownian motion processes, the computation of (1) involves Monte Carlo simulations, unlike the case 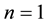 for which (1) has an explicit formula, which is the well-known Black-Scholes formula. Therefore, even assuming classical parametric price processes, pricing basket options still undergo recent developments which include analytical approximations and computationally fast upper and lower bounds [1] . In addition, the parametric model involves parameters that have to be estimated from data and this poses new statistical issues. Even for the case
for which (1) has an explicit formula, which is the well-known Black-Scholes formula. Therefore, even assuming classical parametric price processes, pricing basket options still undergo recent developments which include analytical approximations and computationally fast upper and lower bounds [1] . In addition, the parametric model involves parameters that have to be estimated from data and this poses new statistical issues. Even for the case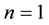 , departures from the classical parametric model have manifested themselves in well-documented volatility smiles and skews and have led to more complicated parametric models whose parameters may be much more difficult to estimate and which also exhibit other lack-of-fit patterns.
, departures from the classical parametric model have manifested themselves in well-documented volatility smiles and skews and have led to more complicated parametric models whose parameters may be much more difficult to estimate and which also exhibit other lack-of-fit patterns.
Hutchinson, Lo and Poggio [2] introduced a nonparametric approach to pricing options, by making the use of basis functions to estimate the pricing function g in the nonparametric regression model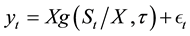 , in which
, in which  denotes the option price and
denotes the option price and 


2. SPD of a Portfolio and Nonparametric Pricing of Basket Options
2.1. Estimation of SPD of an Asset and Option Pricing
Aït-Sahalia and Lo [3] note that one of the most important advances in the economic theory of investment under uncertainty is the Arrow-Debreu preference-based equilibrium model under which the prices of securities that pay $1 (or nothing) in a specific state of nature (otherwise) are given by the SPD. In particular, in an arbitrage-free options market, the SPD 



for a call option, and with 

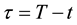

In the classical Black-Scholes model [7] , the underlying asset price process is assumed to follow a geometric Brownian motion 


log-normal distributions as

period. Because of well-documented differences between the Black-Scholes and the actual option prices, more flexible (and also more complicated) models have been proposed for the asset price process under the risk-neutral measure, including the implied volatility function (IVF) model, the stochastic volatility (SV) model, and stochastic volatility with contemporaneous jumps in asset prices and volatilities (SVCJ). Aït-Sahalia and Lo [3] therefore propose to use a semiparametric estimator of SPD, which can in turn provide a robust pricing function for European options. Central to their semiparametric approach is the representation of 

due to Breeden and Litzenberger [8] and Banz and Miller [9] . The semiparametric approach assumes the Black-Scholes pricing function for C but with 


Yuan [6] develops a novel nonparametric estimate of the SPD that can be represented as a nonparametric mixture of log-normal densities. The estimator is defined as the minimizer of the least square criterion 



is the pricing function determines by the Black-Scholes call option price 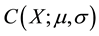






2.2. Nonparametric Pricing of Basket Options via Estimated SPD of Portfolio
Treating the portfolio as an asset, we can follow Yuan’s method described above to estimate the SPD 



where 






Example 1. Consider







where 

Here and in the sequel, we use 








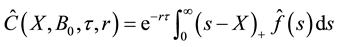

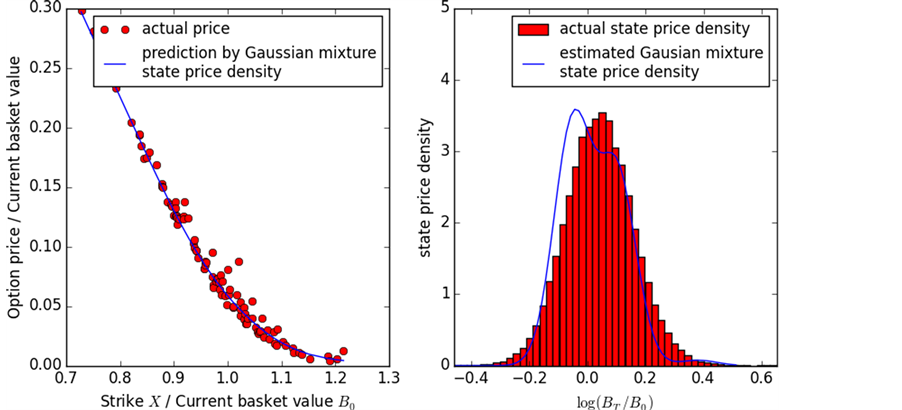
Figure 1. Basket option price (left) and SPD (right) for
Figure 2. Basket option price (left) and SPD (right) for
sults comparing these prices, and also the estimated SPD with the actual density function, for 

2.3. Discussion and Related Literature
The approach to density estimation in this section starts with the application at hand to come up with a representation of the density function. In particular, the choice of Gaussian mixture for the SPD in Yuan (2009) [6] is based on the closed-form expression of the option price when 
In the statistics literature, the use of Gaussian mixture to estimate density function has been studied from the Bayesian perspective that the weight and parameters of each mixture come from some prior distribution. Suppose the data 




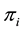




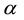
3. Estimation of Joint State Price Density and Pricing Function of Basket Options
Using observed basket option prices to estimate the SPD of the underlying portfolio is unrealistic in practice because basket option is exotic options in over-the-counter markets. In fact, financial engineers make use of data from vanilla options on the underlying assets of the basket to price these exotics. We now describe how the method in Section 2.2 can be modified to estimate the joint SPD of the vector 





where 


The marginal SPD of 




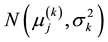
responding weights 
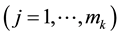
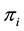

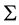






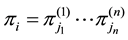


be estimated from historical returns data since the time series of returns are i.i.d random variables in the Gaussian mixture model [6] , yielding a consistent estimate 





Example 2. To illustrate Algorithm 2, this example considers






generated from truncated normal distributions:

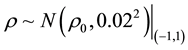






Algorithm 1 (for the 300 calls) the SPD 



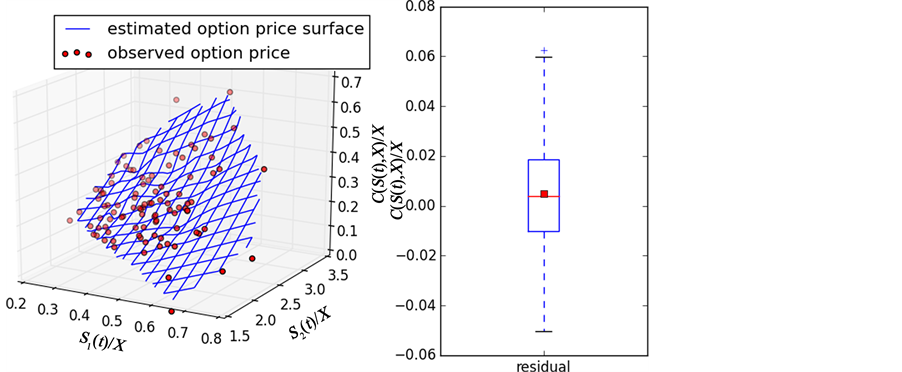
Figure 3. Basket option price using joint state price density for 
Figure 4. Basket option price using joint state price density for 
Estimating the joint SPD in this section seems to be much easier than estimating the joint density of a multivariate distribution in the statistics. It starts by estimating the marginal density of each component of the random vector and then combines them via an estimated correlation matrix in the Gaussian mixture model (6). For multivariate kernel estimators in the statistics literature (see reviews by Scott and Sain [13] and Hwang, Lay and Lippman [14] ), choosing smoothing parameters means choosing a transformation matrix H, in particular the Gaussian kernel becomes


4. Conclusion
The approach used in Sections 2 and 3 to estimate a density function (specifically the SPD) exemplifies an application-driven density estimation methodology that has major differences from traditional density estimators in the statistics literature. Traditional density estimators use kernels of the form




error (IMSE)

where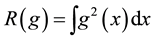

but it cannot be implemented because 


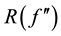




Acknowledgements
This research is supported by the National Science Foundation grant DMS 1407828.
Cite this paper
YumingKuang,Tze LeungLai, (2015) State Price Density Estimation and Nonparametric Pricing of Basket Options. Journal of Mathematical Finance,05,448-456. doi: 10.4236/jmf.2015.55038
References
- 1. Caldana, R., Fusai, G., Gnoatto, A. and Grasselli, M. (2014) General Closed-Form Basket Option Pricing Bounds. Available at SSRN 2376134.
- 2. Hutchinson, J.M., Lo, A.W. and Poggio, T. (1994) A Nonparametric Approach to Pricing and Hedging Derivative Securities via Learning Networks. Journal of Finance, 49, 851-889.
http://dx.doi.org/10.1111/j.1540-6261.1994.tb00081.x - 3. Aït-Sahalia, Y. and Lo, A.W. (1998) Nonparametric Estimation of State-Price Densities Implicit in Financial Asset Prices. Journal of Finance, 53, 499-547.
http://dx.doi.org/10.1111/0022-1082.215228 - 4. Aït-Sahalia, Y. and Duarte, J. (2003) Nonparametric Option Pricing under Shape Restrictions. Journal of Econometrics, 116, 9-47.
http://dx.doi.org/10.1016/S0304-4076(03)00102-7 - 5. Härdle, W. and Yatchew, A. (2001) Dynamic Nonparametric State Price Density Estimation Using Constrained Least Squares and the Bootstrap. Discussion Papers, Interdisciplinary Research Project 373: Quantification and Simulation of Economic Processes No. 2002, 16.
- 6. Yuan, M. (2009) State Price Density Estimation via Nonparametric Mixtures. Annals of Applied Statistics, 3, 963-984.
http://dx.doi.org/10.1214/09-AOAS246 - 7. Black, F. and Scholes, M. (1973) The Pricing of Options and Corporate Liabilities. The Journal of Political Economy, 81, 637-654.
http://dx.doi.org/10.1086/260062 - 8. Breeden, D.T. and Litzenberger, R.H. (1978) Prices of State-Contingent Claims Implicit in Option Prices. Journal of Business, 51, 621-651.
http://dx.doi.org/10.1086/296025 - 9. Banz, R.W. and Miller, M.H. (1978) Prices for State-Contingent Claims: Some Estimates and Applications. Journal of Business, 51, 653-672.
http://dx.doi.org/10.1086/296026 - 10. Ferguson, T.S. (1983) Bayesian Density Estimation by Mixtures of Normal Distributions. Recent Advances in Statistics, 24, 287-302.
- 11. Escobar, M.D. and West, M. (1995) Bayesian Density Estimation and Inference Using Mixtures. Journal of the American Statistical Association, 90, 577-588.
http://dx.doi.org/10.1080/01621459.1995.10476550 - 12. Kuo, L. (1986) Computations of Mixtures of Dirichlet Processes. SIAM Journal on Scientific and Statistical Computing, 7, 60-71.
http://dx.doi.org/10.1137/0907004 - 13. Scott, D.W. and Sain, S.R. (2005) Multidimensional Density Estimation. In: Rao, C.R., Ed., Handbook of Statistics Elvesier, New York, 229-261.
http://dx.doi.org/10.1016/s0169-7161(04)24009-3 - 14. Hwang, J.N., Lay, S.R. and Lippman, A. (1994) Nonparametric Multivariate Density Estimation: A Comparative Study. IEEE Transactions on Signal Processing, 42, 2795-2810.
http://dx.doi.org/10.1109/78.324744 - 15. Sian, S.R., Baggerly, K.A. and Scott, D.W. (1994) Cross-Validation of Multivariate Densities. Journal of American Statistical Association, 89, 807-817.
http://dx.doi.org/10.1080/01621459.1994.10476814 - 16. Duong, T. (2007) ks: Kernel Density Estimation and Kernel Discriminant Analysis for Multivariate Data in R. Journal of Statistical Software, 21, 1-16.
http://dx.doi.org/10.18637/jss.v021.i07