Received 28 June 2015; accepted 2 February 2016; published 5 February 2016

ABSTRACT

In earlier papers, classes of transfer policies have been studied and maximal and minimal Lorenz curves 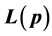obtained. In addition, there are policies belonging to the class with given Gini indices or passing through given points in the 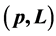plane. In general, a transformation 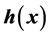describing a realistic transfer policy has to be continuous. In this paper the results are generalized and the class of transfer policies 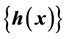is modified so that the members may be discontinuous. If there is an optimal policy which Lorenz dominates all policies in the class, it must be continuous. The necessary and sufficient conditions under which a given differentiable Lorenz curve 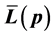can be generated by a member of a given class of transfer policies are obtained. These conditions are equivalent to the condition that the transformed variable 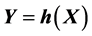stochastically dominates the initial variable X. The theory presented is obviously applicable in connection with other income redistributive studies such that the discontinuity can be assumed. If the problem is reductions in taxation, then the reduction for a taxpayer can be considered as a new benefit. The class of transfer policies can also be used for comparisons between different transfer-raising situations.

Keywords:

Lorenz Dominance, Stochastic Dominance, Tax Policy, Transfer Policy

1. Introduction

Lorenz curves were initially introduced for comparison and analysis of income distributions in a country in different times or in different countries in the same era. Later it has been widely applied in different contexts. Especially, classes of transfer and tax policies have been studied and maximal and minimal Lorenz curves 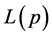obtained. In addition, there are policies with given Gini indices or passing through given points in the 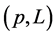plane. Furthermore, the conditions (stochastic dominance) for attainable Lorenz curves have been obtained ([1] , [2] ). These findings have been found under the assumption that the transformation is continuous. In this paper we generalize the results for discontinuous transformations.

2. Notations

We use similar notations as in my previous papers. Let the income be X with the distribution function,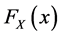

density function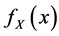, mean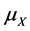, and Lorenz curve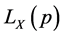. The basic formulae are 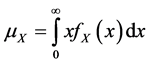and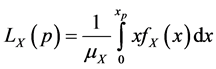, where.

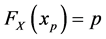We introduce the transformation, where is non-negative and monotone-increasing. Since the transformation can be considered as a tax or a transfer policy, the transformed variable Y is either the post-

tax or post-transfer income. The mean and the Lorenz curve for the variable Y are and.

A general theorem concerning Lorenz dominance ( [3] [4] ) is:

Theorem 1. Let X be an arbitrary non-negative, random variable with the distribution, mean and the Lorenz curve. Let be a non-negative, monotone-increasing function, let and let exist. The Lorenz curve of Y exists and the following results hold:

1) if and only if is monotone-decreasing;

2) if and only if is constant;

3) if and only if is monotone-increasing.

3. Results

Classes of transfer policies. The class of transfer policies

H: (1)

where is non-negative, monotone-increasing and continuous was introduced in ( [5] [6] ). This class was defined in order to compare policies yielding the same transfer effect. Now we modify this class of transfer policies and allow to be discontinuous. Define

H^*: (2)

where is non-negative and monotone-increasing. If is discontinuous, it can have only a countable number of positive finite steps ( [4] [6] ). A discontinuous transformation is sketched in Figure 1.

If an optimal policy exists which Lorenz dominates all policies in H^*, then according to Theorem 1, it must be continuous because has to be monotonically and decreasing, but of every discontinuity point the ratio

cannot be monotonically decreasing. The ratio is outlined in Figure 2.

Consequently, although class (2), also contains discontinuous policies in comparison with initial class H, the policy

(3)

being optimal among all continuous policies, is still optimal, having the Lorenz curve

The inferior Lorenz curve can be obtained from the sequence [7]

(4)

These policies give no benefits to the poorest sector of the population (), but positive benefits to the richest (). We construct the sequence so that H_S Í H^* and that their Lorenz curves converge towards an

inferior Lorenz curve. If we define so that, then every is continuous

and monotone increasing: and. Hence, H_S Í H^* and the corresponding Lorenz curve is

(5)

where ( [7] [8] ).

Assume that, and are chosen so that for all. Consider a sequence, such that, and hence,. We obtain the limit Lorenz curve [7]

(6)

The Lorenz curve is inferior because we can prove [8] .

Theorem 2. The Lorenz curve is inferior to the Lorenz curves for the whole class H^*.

Proof. Consider an arbitrary, continuous or discontinuous policy in H^*. Using the condition, we can evaluate in the following way:

(7)

This inequality holds for all. Consequently, the class H^* of transfer policies containing discontinuous policies satisfies the same properties as the initial class discussed in [5] and [6] . Figure 3 includes a Lorenz curve with a cusp and the Lorenz curves and.

A policy with a given Lorenz curve. In Fellman [6] we obtained necessary and sufficient conditions under which a given differentiable Lorenz curve can be generated by a member of a given class of transfer policies. These conditions are equivalent to the condition by which the transformed variable stochastically dominates the initial variable X.

Now we generalise the results, for discontinuous transformations as well. We have stressed above that can only have a countable number of positive finite steps and that every jump in the transformation results in a cusp in the Lorenz curve.

One has to assume that the Lorenz curve considered is convex and that it is differentiable everywhere

with the exception of a countable number of cusps. The corresponding distribution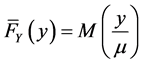, in which

is the inverse function to, with the mean [5] . If has a cusp, then the derivative and the function have jumps. The cumulative distribution functions are outlined in Figure 4.

In general, when the Lorenz curve and the mean are given, the corresponding income distribution is unique. Now we will prove that the conditions already obtained for classes of continuous transformations still hold for class H^*; that is, we will characterise attainable Lorenz curves, although they are not universally differentiable.

The crucial part of this proof is to show that still holds for the distribution [6] . The class H^* of transfer policies containing discontinuous policies satisfies the same properties as the initial class dis-

cussed in [5] and [6] . Following [6] , we obtain the transformation. If

has a cusp for, then has a jump for. The proof in [6] can be applied as such to whenever it is continuous but the discontinuous points need special attention. Consider a neighbourhood

, where is the only discontinuity point of in the interval and

choose a δ > 0 so small that. Let and.

Now, the transformation is continuous for all, and. When

, the inequality holds for the limits and we obtain. Similarly, we obtain

and, when, the inequality holds for the limits and we obtain

. Hence, for all p, and stochastically dominates the initial variable X.

4. Discussion

We have studied the effects of transfer policies in this paper. In general, a transformation describing a realistic transfer policy has to be continuous. However, the theory presented is obviously applicable in connection with other income redistributive studies such that the discontinuity cannot be excluded. If the problem is reductions in taxation, then the tax reduction for a taxpayer can be considered as a new benefit [7] . The class of transfer policies H^* can consequently be used for comparisons between different tax-reducing policies. If changes of transfers are of interest, then the transfer policies can also be applied in transfer-raising situations. If transfers are increased, the effect of increases on a receiver can be considered through transfer policies belonging to H^*. In general, the changes may be mixtures of several different components and discontinuity cannot be excluded. The continuity assumption can be dropped and the class H^* of transfer policies containing discontinuous policies satisfies the same properties as the initial class discussed in ( [5] [6] ). Analogously, tax increases and transfer reductions can be considered as new tax policies [7] . One main result is still that continuity is a necessary condition if one pursues the notion that income inequality should remain or be reduced.

Empirical applications of the optimal policies among a class of tax policies and the class of transfer policies considered here have been discussed in ( [2] [9] ), where we developed “optimal yardsticks” to gauge the effectiveness of given real tax and transfer policies in reducing inequality.

5. Conclusion

We have studied the effects of discontinuous transfer policies. The theory presented is applicable in connection with income redistributive studies such that the discontinuity cannot be excluded. A tax reduction for a taxpayer or a transfer increase on a receiver can be considered as new benefits. In general, such changes may be mixtures of different policy components and discontinuity cannot be excluded. However, one main result is still that continuity is a necessary condition if income inequality should remain or be reduced.

Acknowledgements

This work was supported in part by a grant from the Magnus Ehrnrooths Stiftelse foundation.

Cite this paper

JohanFellman, (2016) Transfer Policies with Discontinuous Lorenz Curves. Journal of Mathematical Finance,06,28-33. doi: 10.4236/jmf.2016.61003

References