Journal of Mathematical Finance
Vol.05 No.03(2015), Article ID:57868,23 pages
10.4236/jmf.2015.53023
Mellin Transform Method for the Valuation of the American Power Put Option with Non-Dividend and Dividend Yields
Sunday Emmanuel Fadugba, Chuma Raphael Nwozo
1Department of Mathematical Sciences, Ekiti State University, Ado Ekiti, Nigeria
2Department of Mathematics, University of Ibadan, Oyo State, Nigeria
Email: emmasfad2006@yahoo.com, crnwozo@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 May 2015; accepted 4 July 2015; published 10 July 2015
ABSTRACT
In this paper we present the Mellin transform method for the valuation of the American power put option with non-dividend and dividend yields, respectively. We use the Mellin transform method to derive the integral representations for the price and the free boundary of the American power put option. We also extend our results to derive the free boundary and the fundamental analytic valuation formula for perpetual American power put option which has no expiry date. Numerical experiments have shown that the Mellin transform method is a better alternative technique compared to the binomial model (BSM), recursive method (RM) and finite difference method (FDM) for the valuation of the American power put option. In general, the Mellin transform method is accurate, flexible and produces accurate prices for the optimal exercise boundary of the American power put option for a wide range of parameters. Hence the Mellin transform method is mutually consistent and agrees with the values of the analytic option valuation formula called the “Black- Scholes model”.
Keywords:
American Power Option, Dividend Yield, Mellin Transform Method, Non-Dividend Yield, Perpetual Power Put Option

1. Introduction
Option valuation has been studied extensively in the last three decades. Many problems in financial mathematics entail the computation of a particular integral. In many cases these integrals can be valued analytically and in some cases they can be computed using a partial differential equation, or valued using numerical integration.
Power option is defined as a contingent claim on the product of powers of several underlying assets. The holder has either the right, but not the obligation to buy, as in the case of the power call option, or the possibility to sell, as in the case of the power put option, an asset for a certain price at a prescribed date in the future. The difference between the American and the European power options is that the European power option can only be exercised at the maturity or expiry date while the American power option can be exercised by its holder at any time before the expiry date. This early exercise feature makes the valuation of the American power option mathematically challenging and therefore, creats a great field of research.
A perpetual American power option is an option that has no expiry date. In other words, this type of power option never expires. In a special case of a plain vanilla perpetual option, a closed form solution for the free boundary and price of the American put was derived by [1] .
Mellin transforms in option theory were introduced by [2] , [3] extended the results obtained in [2] and showed how the Mellin transform approach could be used to derive the valuation formula for the perpetual American put options on dividend-paying stocks. [4] considered the Mellin transform method for the valuation of some vanilla power options with non-dividend yield. They derived the fundamental valuation formula known as the Black-Scholes model using the convolution property of the Mellin transform method. The analytical valuation of the American options was considered by [5] . An alternative approach to the valuation of American options and applications was considered by [6] .
For the mathematical background of the Mellin transform method in derivatives valuation see [7] -[15] , just to mention few. In this paper, we focus on the Mellin transform method for the valuation of the American power put option with non-dividend and dividend yields, respectively, and its extension to power option which has no expiry date, i.e. “perpetual American power put option”. The rest of the paper is structured as follows: in Section 2, we present American power options and the payoffs for power call and put options. Section 3 presents the Mellin transform method for the valuation of the American power put option. Section 4 considers the extension of the Mellin transform method to the valuation of the perpetual American power put option. In Section 5, we present some numerical experiments. Section 6 concludes the paper.
2. American Power Options
The power options can be seen as a class of options in which the payoff at expiry is related to the 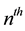 power of the underlying price of the asset. American power options are options that can be exercised before or at the expiry date with non-linear payoff. The American power option comes in two forms, namely, the American power call option and the American power put option. The American power call option is an option with non- linear payoff given by the difference between the price of the underlying asset at maturity raised to a strictly positive power and the exercise price. The American power put option is an option with non-linear payoff given by the difference between the exercise price and price of the underlying asset at maturity raised to a strictly positive power. For an American power option on the underlying price of the asset
power of the underlying price of the asset. American power options are options that can be exercised before or at the expiry date with non-linear payoff. The American power option comes in two forms, namely, the American power call option and the American power put option. The American power call option is an option with non- linear payoff given by the difference between the price of the underlying asset at maturity raised to a strictly positive power and the exercise price. The American power put option is an option with non-linear payoff given by the difference between the exercise price and price of the underlying asset at maturity raised to a strictly positive power. For an American power option on the underlying price of the asset 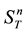 with exercise price K and time to expiry T, we have the payoffs for the American power call and put options as
with exercise price K and time to expiry T, we have the payoffs for the American power call and put options as
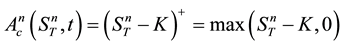 (1)
(1)
and
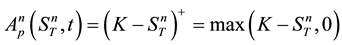 (2)
(2)
respectively.
Remark 1
・ For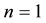 , the payoffs for American power call and put options in (1) and (2) become the payoffs for plain American call and put options, i.e.
, the payoffs for American power call and put options in (1) and (2) become the payoffs for plain American call and put options, i.e.
 (3)
(3)
and
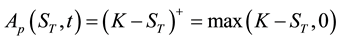 (4)
(4)
respectively.
3. The Mellin Transform Method for the Valuation of the American Power Put Option
There are many methods for the valuation of the American power option leading to different but equivalent mathematical formulations. We consider the derivation of the integral representation for the price of the American power put option and the integral equation to determine the free boundary of the American power put option via the Mellin transform method for the case of both non-dividend and dividend yields.
3.1. American Power Put Option with Non-Dividend Yield
Consider the non-homogeneous Black-Scholes partial differential equation for the American power put option with non-dividend yield given by
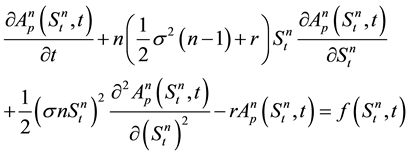 (5)
(5)
where the early exercise function f defined on 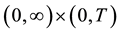 is given by
is given by
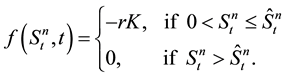 (6)
(6)
The final time condition given by 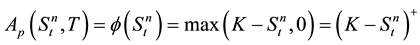 on
on  is called the high contact condition. The other boundary conditions are given by
is called the high contact condition. The other boundary conditions are given by
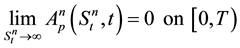 (7)
(7)
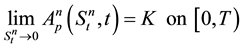 (8)
(8)
The free boundary 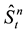 is determined by the smooth pasting conditions given by
is determined by the smooth pasting conditions given by
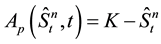 (9)
(9)
and

Applying the Mellin transform to (5), we have that

Setting 


The Mellin transform of the early exercise function in (12) is obtained as

Solving further, we have the particular solution of (12) as

The complementary solution to the left hand side of (12) is obtained as

where 



Using (16) and (17) in (15) we have that

Hence the general solution to (12) is given by

The Mellin inversion of (19) is obtained as

where 
Remark 2
・ The first term in (20) is the integral representation for the price of the European power put option (stems from the minimum guaranteed payoff of the American power put) which pays no dividend yield (see [4] ). The second term in (20) is called the early exercise premium (the value attributable to the right of exercising the option early) for the American power put option with non dividend yield denoted by

where
・ Setting 

where
We formalized the properties highlighted in Remark 2 in the following results.
Theorem 1 The American power put option 
where 


Theorem 2 Using the smooth pasting conditions given by 

boundary formulation of the American power put option with non-dividend yield is given by
3.2. American Power Put Option with Dividend Yield
The derivation of the integral representation for the price of the American power put option which pays dividend yield using the Mellin transform method is given in the following result.
Theorem 3 Let 



Proof. Consider the non-homogeneous Black-Scholes partial differential equation for the American power put option with dividend yield given by

where

on 




and

The Mellin transform of (24) gives

Putting 


where

Following the same procedures for the case of non-dividend yield, the general solution to (30) is obtained as

The Mellin inversion of (31) is given by

Equation (32) is the integral representation for the price of American power put option with dividend yield, where 

Remark 3
・ The first term in (32) is the integral representation for the price of the European power put option (stems from the minimum guaranteed payoff of the American power put) with dividend yield and the last two terms denote the early exercise premium (the value attributable to the right of exercising the option early) for the American power put option with dividend yield denoted by

where
・ Setting 

where
From Remark 3, we have the following results.
Theorem 4 The American power put option 
where 


Theorem 5 Using the smooth pasting conditions given by 

the free boundary formulation of the American power put option with dividend yield is given by
The following results present some special cases of (20) and (32).
Theorem 6 If 

(i) The integral representation for the American power put option which pays no dividend yield (20) reduces to the integral equation derived by Kim [6] for the price of the plain American put option given by

where

(ii) The free boundary for the American power put option which pays no dividend yield (22) reduces to the integral equation derived by Kim [6] for the price of the plain American put option given by

where

Proof. Setting 


where 


where 


where

The early exercise function is given by

and

Using the convolution property of the Mellin transform, (42) becomes

Substituting the value of the early exercise function 

into (45), we have that

Using the transformation given by

(47) becomes

Substituting (49) into (41) we have the early exercise premium for the American put option with non-dividend yield as

where

Setting

where
Substituting (52) into (40) we get the integral equation (35) obtained by Kim [6] as
Hence (i) is established. For the second reduction, setting 
using the smooth pasting conditions given by 

dary 
where
Theorem 7 If



Proof. Let 


where 


where



and

Notice first that critical stock price is bounded from above i.e.


and

respectively. If

We have

Using (63), the limit of (55) is obtained as

Since
and
Then (64) becomes

If
We have that

The first integral 

Applying the residue theorem of complex number given by

Then the inner integral in (67) becomes

Substituting (69) into (67) yields

Similarly,

Substituting (70) and (71) into (66) for

Using the l’Hospital rule, for

Combining (72) and (73)
Hence (53) is established.
Remark 4
The above results confirm the formula of Kim and Yu [6]
Theorem 8 If the underlying asset price follows a lognormal diffusion process and the interest rate is a positive constant, then the optimal exercise boundary of the American power put option with 

Proof. Let


If


If


Combining (75) and (76), we have the optimal exercise boundary of the American power put option with 
Hence (74) is established.
Remark 5
From (75), we notice that when 
From (76), we deduce that when 
Theorem 9 The integral representation for the price of the American power put option which pays dividend yield given by (32) can be reduced to integral representation derived by Kim [6] .

where
Proof. Setting

where 


Using the procedures of [3] , (78) can be written as

with the Mellin transforms of 



respectively. Using the convolution theorem of the Mellin transform we have that
The price of the American power put option which pays dividend yield can be expressed as

The integral 

where 

transformation given by
and
For the first and second integrals in (83) respectively, we have that

Substituting (84) into (82) yields

By changing

Hence by setting
4. Application of the Results to Perpetual American Power Put Option Valuation
Now, we apply the results generated for the integral equations in (20) and (32) to power options which have no expiry date. The following results shows the derivation of the expression for the free boundary of perpetual the American power put option and its closed form solution for both non-dividend and dividend yields, using the Mellin transform method.
Theorem 10 (Non-Dividend Yield) If 


and the price of the perpetual American power option becomes

where

Proof. The integral representation for the price of the American power put option which pays no dividend yield given by (20) can be expressed as

where 


with
and

respectively. For (90) to hold as




Differentiating (91) at 

where

As 

Also differentiating (92) yields

Taking the limit of (97) as

Therefore,

where 





Since

Substituting (96) and (101) into (93) yields

Equation (102) is the expression for the free boundary of a perpetual American power put option. Next, we use (102) to derive an expression for the price of perpetual American power put option



where

Once again we apply the residue theorem (68) to get

Equation (105) is the price of a perpetual American power put option obtained as a limit of the price of a finite-lived American power put option.
Theorem 11 (Dividend Yield) If 


and the price of perpetual American power put option equals

where

and

Proof. The integral representation for the price of the American power put option which pays dividend yield given by (32) can be expressed as

where



with


respectively. The roots of 
and
Thus we write that
with





petual power put which pays dividend yield can be written as

Differentiating (111) at 

where

As 

Now differentiating (112) w.r.t 


Therefore, by setting 

Let 

In the same manner, setting 

Therefore,

Setting 

Once again by the application of residue theorem (68), then (120) and (122) yield

and

respectively. Substituting (117), (123) and (124) into (114), we obtain

Equation (125) is called the free boundary of the perpetual American power put option which pays dividend yield.
The price for the perpetual American power put option is given by

Using the residue theorem (68), then (126) becomes

5. Numerical Experiments
In this section we present some numerical experiments and discussion of results.
Experiment 1
We consider the valuation of the American power put option for 

The result generated is shown in Table 1 below.
Experiment 2
We consider the valuation of the American power put option for 
The results generated for the price of the American power put option via Black-Scholes model (BSM), binomial model (BM) and the Mellin transform method (MTM) are shown in Tables 2-4 below. Also the results generated for the free boundary of the American power put option are shown in Tables 5-7 below.
Experiment 3
We consider the valuation of the American Power put option with the following parameters:
The comparative results analysis of the Mellin transform method (MTM) in the context of Black-Scholes model (BSM), binomial model (BM), recursive method (RM) and Finite difference method (FDM) are shown in Table 8.
Table 1. American power put values.
Table 2. The price of American power put option using
Table 3. The price of American power put option using
Table 4. The price of American power put option using
Table 5. The free boundary of American power put option using
Table 6. The free boundary of American power put option using
Table 7. The free boundary of American power put option using
Table 8. The comparative results analysis of some numerical methods for the valuation of American power put option.
Discussion of Results
From Figure 1 below, we observe that the higher the volatility, the higher the values of the American power put option. Also the higher the power of the American put option, the lower the values of the option. Figures 2-4 below show that the Mellin transform method is mutually consistent, performs very well, accurate and agrees with the values of Black-Scholes model (BSM). In Figure 5 below, we plot the free boundary 

6. Conclusion
In this paper, we have derived the integral representations for the price and the free boundary of the American power put option for non-dividend and dividend yields using the Mellin transform method. We also extended the integral equation for the price of the American power put option to derive the expression for the free boundary and the price of the perpetual American power put option which pays both non-dividend and dividend yields as the limit of a finite-lived option by means of smooth pasting condition. In general, numerical experiments have shown that the Mellin transform method is accurate, flexible, efficient and produces accurate prices for the optimal exercise boundary for a wide range of parameters.
Figure 1. American power put option values using Table 1.
Figure 2. The comparative results analysis using Table 2.
Figure 3. The comparative results analysis using Table 3.
Figure 4. The comparative results analysis using Table 4.
Figure 5. The free boundaries of American power put option with n = 1.
Figure 6. The comparative results analysis using Table 8.
Cite this paper
Sunday EmmanuelFadugba,Chuma RaphaelNwozo, (2015) Mellin Transform Method for the Valuation of the American Power Put Option with Non-Dividend and Dividend Yields. Journal of Mathematical Finance,05,249-272. doi: 10.4236/jmf.2015.53023
References
- 1. Samuelson, P.A. (1965) Rational Theory of Warrant Pricing. Industrial Management Review, 6, 13-31.
- 2. Panini, R. and Srivastav, R.P. (2005) Pricing Perpetual Options Using Mellin Transforms. Applied Mathematics Letters, 18, 471-474.
http://dx.doi.org/10.1016/j.aml.2004.03.012 - 3. Frontczak, R. and Schöbel, R. (2008) Pricing American Options with Mellin Transforms. Working Paper.
- 4. Nwozo, C.R. and Fadugba, S.E. (2014) Mellin Transform Method for the Valuation of Some Vanilla Power Options with Non-Dividend Yield. International Journal of Pure and Applied Mathematics, 96, 79-104.
http://dx.doi.org/10.12732/ijpam.v96i1.7 - 5. Kim, I. (1990) The Analytic Valuation of American Options. The Review of Financial Studies, 3, 547-572.
http://dx.doi.org/10.1093/rfs/3.4.547 - 6. Kim, I. and Yu, G.G. (1996) An Alternative Approach to the Valuation of American Options and Applications. Review of Derivatives Research, 1, 61-85.
http://dx.doi.org/10.1007/BF01536395 - 7. Erdelyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. (1954) Tables of Integral Transforms, Vol. 1-2. McGraw-Hill, New York.
- 8. Fadugba, S.E. and Nwozo, C.R. (2015) Integral Representations for the Price of Vanilla Put Options on a Basket of Two-Dividend Paying Stocks. Applied Mathematics, 6, 783-792.
http://dx.doi.org/10.4236/am.2015.65074 - 9. Frontczak, R. and Schöbel, R. (2009) On Modified Mellin Transforms, Gauss-Laguerre Quadrature and the Valuation of American Call Options. Tübinger Diskussionsbeitrüge, No. 320.
- 10. Gradshteyn, I. and Ryshik, I. (2007) Table of Integrals Series and Products. 7th Edition, Academic Press, Waltham.
- 11. Panini, R. and Srivastav, R.P. (2004) Option Pricing with Mellin Transforms. Mathematical and Computer Modelling, 40, 43-56.
http://dx.doi.org/10.1016/j.mcm.2004.07.008 - 12. Vasilieva, O. (2009) A New Method of Pricing Multi-Options Using Mellin Transforms and Integral Equations. Master’s Thesis in Financial Mathematics, School of Information Science, Computer and Electrical Engineering, Halmstad University, Halmstad.
- 13. Nguyen, T.H. and Yakubovich, S.B. (1991) The Double Mellin-Barnes Type Integrals and Their Applications to Convolution Theory. World Scientific, Series on Soviet Mathematics, Vol. 6, Singapore, 295p.
- 14. Zemanian, A.H. (1987) Generalized Integral Transformations. Dover Publications, New York.
- 15. Zieneb, A.E. and Rokiah, R.A. (2011) Analytical Solution for an Arithmetic Asian Option Using Mellin Transforms. International Journal of Mathematical Analysis, 5, 1259-1265.





























































