Journal of Mathematical Finance
Vol.05 No.01(2015), Article ID:53612,13 pages
10.4236/jmf.2015.51003
Testing Continuous-Time Interest Rate Model for Chinese Repo Market
Huimin Zhao*, Fangping Peng
Sun Yat-Sen Business School, Sun Yat-sen University, Guangzhou, China
Email: *zhaohuim@mail.sysu.edu.cn, pengfp@mail.sysu.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 January 2015; accepted 26 January 2015; published 29 January 2015
ABSTRACT
This paper tests the popular continuous-time interest rate models for Chinese repo market to address what and how the interest rates change with the marketlization in China. Using Bandi [1] ’s method, we get the functional nonparametric estimation of drift and diffusion terms and the local time of the process. We find that the interest rates of China during the period from 1993 to 2003 are bimodal distributed and propose a two-regime model which can fit the data better. We also study the probabilities that the process will stay the two regimes respectively and its transition probability that the process transfers from one regime to another regime.
Keywords:
Chinese Repo Market, Interest Rate, Nonparametric Estimation

1. Introduction
The short rate is fundamental to the pricing of fixed-income securities. Large literature devotes itself to the esti- mation of the short term interest rate process using different models and methods. In continuous time finance, the dynamic evolution of the spot interest rate process is usually driven by a Markov stochastic differential equ- ation. Diffusion processes have become the standard tool for modelling prices in financial markets for derivative pricing and risk management purposes. Although such continuous time processes offer analytic tractability, the parameters of the process are often difficult to estimate from the data because sample data are available only at discrete time points.
Literature has documented different parametric models for short rate dynamics, each attempting to capture particular features of observed interest rate movements. However, empirical tests of these models have yielded mixed results. Therefore, nonparametric techniques are well-used to remove some distributional restrictions im- posed by parametric models.
Ait-Sahalia [2] compares their implied parametric density to the same density estimated nonparametrically and finds strong evidence that CEV diffusions with linear drifts do not fit the data well. Stanton [3] employs the first-order nonparametric method to estimate drift and diffusion of the short rate, whose results also indicate that there is substantial evidence of nonlinearity in the drift. Jiang and Knight [4] investigate the finite sample properties of various estimators using the Monte Carlo simulation. They observe that while all the parametric diffusion estimators perform well, the parametric drift estimators perform poorly. Moreover, both the nonparametric diffusion and drift estimators perform reasonably well.
An assumption commonly made in nonparametric methods is the stationarity of the process. Notwithstanding the advantages of assuming stationarity, it would be helpful to allow for martingale and other possible forms of non-stationary behavior in the process. Motta and Hafner [5] study locally stationary factor models by the nonparametric estimation. Florens and Simoni [6] investigate the nonparametric estimation of an instrumental regression. Restrepo-Tobn and Kumbhakar [7] apply nonparametric estimation to study US banks. Kristensen [8] tests a diffusion model by nonparametric estimation.
Bandi and Philips [9] construct a nonparametric method for scalar diffusion models without imposing the stationary assumption. They assume recurrence which is less restrictive than stationarity. Bandi and Neuyen [10] derive the properties of local time. They also develop a procedure for estimating functions non-parametrically from data observed only at discrete time intervals based on US short rate data. Johannes [11] applies the same method on US 3-month Treasury bill data even though his results reflects negatively on one-factor diffusion model.
There is no large literature investigating Chinese short interest rate market. Interest rates can be regarded as a benchmark to distribute rare capital by interest rate mechanism in the financial market. It is meaningful to study whether the interest rate is decided by the mechanism of market competition or not. Hong and Lin [12] test the discrete-time model for the Chinese spot interest rate. Most of literature focuses on the term structure model or monetary policy of China, such as Duffee and Stanton [13] , Siegel [14] and He and Wang [15] .
In this paper, we study the interest rate behavior of China based on the observed 7 days repo rate for Shanghai market. The repo rate provides the benchmark for the interest rate of marketability and pricing of national debt futures. With the interest rate marketlization of China, the movement of interest rate reflects the principle of the supply and demand tightly. We follow Bandi and Philips [9] ’s method to assume recurrence only and examine how well it could fit China data under non-parametric model without stability. We find that the interest rates behaved very differently during the two subperiods, so we assume the density of the process is bimodal. Based on the evidence of local time of sub-sample data, we estimate the parameters for a two regime model with the year 1999 as the change point.
The paper is organized as follows. Section 2 introduces the data and method. Section 3 gives the empirical results. Section 4 discusses the two-regime model and its properties implied by the empirical results. Conclusions are given in Section 5.
2. Data and Method
2.1. Data
We use 7-day repo rate of Shanghai market of China as the proxy of Chinese repo market. The data are retrieved from database of China Center for Economic Research (CCER) of Peking University. On the pre-holiday days such as the one-week holiday on the labor day, National day and Chinese new year, the interest rates are abnor- mally high since they are not real interest rates for 7 days, so I removed these from my observations. The final data set is composed of 2052 daily observations from January 4, 1995 to December 31, 2003. The short rate is continuously compounded yield to maturity. Figure 1 gives the changing of time series of the sample data.
From Figure 1, it is clear that the data has a different feature before and after 1999. Before 1999, interest rates stayed at a higher level, but they dropped dramatically after 1999. This is consistent with the change of term structure in Chinese money market. Figure 1 also shows the daily change (difference between the two successive days) of the spot rates. It also shows similar pattern with the daily data: interest rates become less volatile since 1999.
We study the behavior of short interest rates by two sub-samples 1995.01-1998.12 and 1999.01-2003.12. The results of preliminary analysis of the whole sample and sub-samples are shown in Table 1. Panel A presents
Figure 1. The figures shows the daily time-series and daily changes of 7-day repo rate for Shanghai market respectively. The sample period is 1995.01-2003.12 (2052 observations).
Table 1. Descriptive statistics of repo rate and hypothesis test.
This table presents the mean, standard deviation, skewness, kurtosis, and the first autocorrelation of the daily data and daily change of entire sample period and two subperiods. It also gives the hypothesis test about mean and variance of daily rate and daily change rate of two subperiods respectively. Panel E and F give the Wilcoxon Rank Sum test to test whether two subperiods have the same distribution.
the statistics of continuously compounded annualized daily repo rate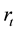 . The first autocorrelation of whole sample is close to 1, and two subperiods have significant different means, standard deviations and skewness. After 1998, interest rates have a higher mean, higher positive skewness and lower volatility. With the market- lization of interest rates, the distribution of them may become more asymmetry because of the stochastic market. Panel B gives the summary statistics of daily change of repo rate
. The first autocorrelation of whole sample is close to 1, and two subperiods have significant different means, standard deviations and skewness. After 1998, interest rates have a higher mean, higher positive skewness and lower volatility. With the market- lization of interest rates, the distribution of them may become more asymmetry because of the stochastic market. Panel B gives the summary statistics of daily change of repo rate . The first autocorrelation of the daily change is lower and negative with a negative and positive kurtosis.
. The first autocorrelation of the daily change is lower and negative with a negative and positive kurtosis.
Panel C shows the result of hypothesis test for daily rate. It shows that the two subperiods have significant different means and variances. But this may induce that the stationarity of the whole data cannot be guaranteed. Using the same hypothesis test with the Panel C, I tested for daily change of the two subperiods in Panel D. The null hypothesis that the two subperiod samples have the volatility was rejected at 1% level.
Furthermore, from Panel A and Panel B of Table 1, the skewness and kurtosis of repo rate and daily change rate are not consistent based on the Wilcoxon Rank Sum test in Panel E and F. This test is a nonparametric alternative to test whether the two samples have the same distribution when their distribution are not known. We find that the two subperiod data follow the different distributions with the different mean and variance. This means that the stationarity of the whole data process may not be guaranteed. Table 2 shows the result for the linear stationary test. The null hypothesis of a unit root was rejected at 5% level based on the augmented Dickey-Fuller test (ADF, see Harvey [16] ).
Figure 2 gives the frequency histogram of the whole data. The height presents the times that the repo rate appears in a small vicinity of a point. It is clear that there are two peaks in the figure at about 3% and 11%.
Based on the above analysis using the repo rate data sample, we add a state variable into our model for our empirical study.
2.2. The Model
We assume that the short rate follows a stochastic differential equation as follows:
 (1)
(1)
where 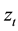 is a standard Brownian motion,
is a standard Brownian motion, 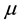 and
and 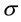 are the drift and diffusion of interest rate process respectively which depend on the values of the short rate
are the drift and diffusion of interest rate process respectively which depend on the values of the short rate 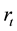 and a state variable
and a state variable 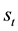 which has two states 1 and 2. Models such as interest rate models of Cox, Ingersoll and Ross (CIR) [17] , Vasicek [18] , Hull and White [19] are special cases of this model.
which has two states 1 and 2. Models such as interest rate models of Cox, Ingersoll and Ross (CIR) [17] , Vasicek [18] , Hull and White [19] are special cases of this model.
But parametric interest rate models may not fit historical data well. Ait-Sahalia [2] reject “ every para- metric model of the spot rate [previously] proposed in the literature”. Jiang and Knight [4] also think that the
every para- metric model of the spot rate [previously] proposed in the literature”. Jiang and Knight [4] also think that the
Table 2. Unit root test for repo rate.
This table presents the statistics of Augmented Dickey Fuller T test for the daily annualized yield on repo rate for Shanghai market. The model used in the test is: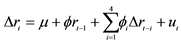 . Panel A reports the estimates of parameters with standard error and t-statistics. Panel B reports the test of unit root. The sample period is 1995.01-2003.12.
. Panel A reports the estimates of parameters with standard error and t-statistics. Panel B reports the test of unit root. The sample period is 1995.01-2003.12.
Figure 2. This figure shows that frequency histogram of time- series of 7-day repo rate for Shanghai market. The sample period is 1995.01-2003.12.
parametric drift estimator performed very poorly. Therefore, we follow the nonparametric estimation techniques which is popular in recent literature related.
The basis for our Monte Carlo simulation is a time-discretization of (1) over a daily interval (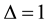 day)
day)
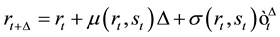 (2)
(2)
where 

After the drift and diffusion estimates are obtained, the next short rate will be simulated according to this data-generating process. After repeating this process a large number, G, sample paths from the true continuous- time model are produced, then the Mento Carlo confidence bands can be determined.
2.3. Nonparametric Estimation Method
As Johannes [11] mentioned, nonparametric estimation method firstly requires little prior information relating to the functional form of the conditional expectations, so it doesn’t need to estimate the type of the function as parametric estimation. Second, nonparametric estimators focus on local effects. This implies that the abnormal or very volatile sub-sample will not change any of the conclusion. The final advantage of nonparametric esti- mation method is that the estimators are feasible and easy to evaluate.
Based on the nonparametric model of Stanton [3] and econometric estimation, which is wildly used by Jiang [20] , Bandi [1] and Johannes [11] , we suppose that the short rate process follows one factor model, not consider- ing the state variable 






where the parameters in Equations (3) and (4) are the same as in Equation (2).
The estimators of drift and diffusion terms are:


where 

where 




This nonparametric method has been developed but they either rely on the existence of a time-invariant mar- ginal density for the underlying process (Jiang [20] , Jiang and Knight [4] ), or stationarity which is assumed despite robustness to deviation from it (Stanton [3] ). So Bandi [1] proposes local time to describe the data. Based on our previous analysis, stationarity of the short rate process cannot be guaranteed, so we also use local time to grasp more information of data.
2.4. Local Time
Bandi [1] uses new fully functional methods to exploit the spatial properties, embodied in the local time (classical references are Chung and Williams [22] ; karatzas and Shreve [23] ; Revuz and Yor [24] ) of interest rate which is robust against deviations from stationarity. Spatial densities and their functionals can be regarded as new descriptive tools for the series that are non-stationary or stationarity cannot be guaranteed, as in Bandi [1] which assume recurrence, a weaker assumption than the stationary condition.
Definition 1 If 




This formula gives the amount of time in real time units that the process 

Recurrence requires the continuous trajectory of the process to visit any set in its range an infinite number of times over time almost surely. It makes economic sense because interest rates are expected to return to the values in their range over and over again. It is meaningful to estimate the drift and diffusion functions at each point in the range of the sample interest rate process. The density of the observations plays a role in the operation of the asymptotic. This information is contained in the estimated local time of the spot interest rate process.
In order to show precise inference on the drift of process of a point (i.e., to achieve statistically consistent esti- mates), we require the estimated local time of the process at that point to be large. Its properties and estimation are shown in the following section.
3. Empirical Results
3.1. Nonparametric Estimation
According to the previous analysis, we derive the estimation of drift and diffusion from the above estimators in Equations (5) and (6) and obtain the 1000 simulated interest rate paths using the Monte Carlo simulation method. Then we estimate the drift and diffusion for every path.
Drift and diffusion estimates for the single-factor model in Equation (1) and their Monte Carlo confidence bands are given in the Figure 3. We report estimates from Equations (3) and (4) for
The simulation results indicate that the estimates are unbiased. Because there are few observations are high rates, the confidence intervals are relatively wide. Especially the diffusion estimation fits well based on Figure 3. At lower interest rate levels, it has a lower variance. As interest rates go up, variance increases accordingly.
3.2. Local Time Estimation
Local time gives the amount of time that the process spends in the vicinity of one point. Bandi [1] also derive the estimator of local time:

By virtue of recurrence, interest rates may visit every level over time which opens up the possibility of re- covering the true function by using a single trajectory of the process over a long time, through a combination of
infill and long span asymptotic. Bandi [1] suggest that the asymptotic 95% confidence interval for 

where the parameters in Equations (8) and (9) are consistent in the whole paper. These asymptotic confidence bands resemble conventional intervals for probability densities.
Figure 4 gives the plot of local time of the short rate of the entire data sample (2167 daily observations). The modes show up at around 3% and 11%. Given the features of the estimation procedure in Bandi [1] , we expect to be able to identify the functions of interest rate at points that are visited frequently. After a quick look at the
Figure 3. The figure shows that the result of nonparametric estimates of drift and diffusion terms the single-factor diffusion model respectively. The sample period is from January 1995 to December 2003 (2052 daily observations). The solid line is the drift function estimated from repo rate data and the dot lines are 95% Monte Carlo confidence bands.
Figure 4. The figure shows that the estimates of local time process of the repo rate series examined in this study. The sample period is January, 1995 to December, 2003 (2052 annualized daily obser- vations). The straight line is the pointwise nonparametric estimates of the local time process and the dot lines are the corresponding 95% asymptotic confidence bands.
graph of the estimated local time, we anticipate that problems would arise in the 17% - 21% range, as the time spent by the sample process in this range is quite small. The density in the figure is bimodal, the spatial density of the process appears to be bimodal. Compared with the frequency histogram of the repo rate in Figure 3, we can find that they are very similar. Therefore, the local time can be the approximation of density of the one path for the underlying process.
From the feature of the data, the interest rates had a higher level before 1999,, but after 1999, interest rates went down and kept a lower level until 2003. Therefore, two different time horizon can be considered: 1995.01- 1998.12 and 1999.01-2003.12. Figure 5 presents their local time estimation respectively.
We find that the two peaks in Figure 4 appear in Figure 5 separately. For the time horizon 1995.01-1998.12, the interest rates below 5% have a very low frequency. For the time horizon 1999.01-2003.12, because 98% of data is below 5%, local times for interest rates above 5% are close to zeros. These features provide the evidence to consider the effect of a state variable.
Figure 6 shows that the drift estimation using the non-parametric estimation method for the two subperiods 1995.01-1998.12 and 1999.01-2003.12 respectively. It can be seen that the drifts are very close to zeros for two subperiods, but other parts below 4% and above 14% for subperiod 1995.01-1998.12 are mean-reversion. It is surprising that for subperiod 1999.01-2003.12, mean-reversion speed is very low for 1% - 5%, especially from 2.5% - 5%, the drifts behave like a martingale. At the same time, from the corresponding local time figures, they have higher local time and cover more than 98% of subperiod data respectively.
This pattern appears again for their diffusion estimation in Figure 7. The corresponding variances over two subperiods are low and relative stable. The Monte Carlo 95% confidence bands are very close. This means that the data have a big change after 1999. Considering their different states, we use two-regime model to fit the data in the follows.
4. Discussion
4.1. Two Regime Model
From the previous analysis, we consider the effect from the state variable. The model is the following:

Figure 5. Figures show the local time process of the repo rate series for two sample periods respectively. The first sample period is from January, 1995 to December, 1998 (939 annualized daily observations). The second sample period is from January, 1999 to December, 2003 (1113 annualized daily observations). The straight line is the pointwise nonparametric estimates of the local time process and the dot lines are the corresponding 95% asymptotic confidence bands.
Figure 6. Figures show that the result of estimates of drift term for the single-factor diffusion model for two subperiods respectively. The sample periods are from January 1995 to December 1998 (939 daily observations) and from January 1995 to December 1998 (939 daily observations). The solid line is the drift function estimated from repo rate data and the dot lines are 95% Monte Carlo confidence bands.
where 
When process 




When 



Figure 7. Figures show that the result of estimates of diffusion term for the single-factor diffusion model for two subperiods respectively. The sample periods are from January 1995 to December 1998 (939 daily observations) and from January 1995 to December 1998 (939 daily observations). The solid line is the drift function estimated from repo rate data and the dot lines are 95% Monte Carlo confidence bands.
We then obtain the estimation of the conditional probability 


babilities





Then from the Equation (10), we consider the model relying on the state variable. The probability 



Based on the previous analysis for drift and diffusion terms, we assume that 


where j = 1 or 2 and
















Given the discrete data, the data generating process is:

where

In our model, we only have two states and 





are:
So for a two-state Markov chain, the transition matrix is
No loss of generality, we assume that this two-state Markov chain is ergodic provided that


The unconditional probability that the process will be in regime 1 at any given date should be the follows:
It is obvious that
The matrix of m-period-ahead transition probabilities for an ergodic two-state Markov chain is given by:
Thus, if the process is currently in state 1, the probability in state 2 after m periods later is given by
where
Given a short rate, whether it stay in regime 1 or 2 is unknown, but we can estimate the probability for any states.
4.2. Estimation of Two Regime Model
From Hamilton [25] , there is the maximum likelihood estimation from the observed data 

where let 
bability 



We suppose virtually certainty from observations from regime j, so that 
Following the method of Hamilton [26] , the EM algorithm is:
where
Because we know
and
Using the whole data sample (2052 observations), we calculate the smoothed probabilities 
It is known that 



This means that once the process enters a regime, it will remain in that state with a high transition probability. Furthermore, in regime 1, mean-reversion parameter is larger, but it is different for regime 2 in which the drift coefficient is very close to zero. These are very reasonable, because the interest rates are lower and not so volatile as regime 1. Both average change rates of two regimes are very close to 0, but their variances differ.
The inference about the value of 



It is obvious that after 1999 probability was very high and close to 1 most of the time. In reality, it is known that when Chinese interest rates remain at a lower level, high economic growth rate gives pressure towards lower rates. Interest-rate liberalization in China is necessary.
5. Conclusions
In this paper, I study the interest rate behavior of China based on the observed 7 days repo rate of Shanghai market. The repo rate provides the benchmark for the interest rate of marketability and pricing of national debt futures.
Following Bandi and Philips [9] ’s method, we assume recurrence only and examine how well it can fit China data under the non-parametric model. Because we find that interest rates behave very differently during the two subperiods which is against the stationarity of the short rate process, we assume that the drift and diffusion terms in the interest rate model rely not only on the short rate, but also on a state variable.
We find that the density of the process is bimodal. Two regime model could be better to capture the interest
Table 3. Two regime model for repo rate.
This table presents the result of two regime model and the data generating process is:



Figure 8. This figure shows that result of probability that the short rate is in state 2 which is at a low level or 
rates of China. Based on the evidence of local time of sub-sample data, we estimate the parameters and examine the properties of two-regime model. Using functional nonparametric method, we test the Vasicek model at different states. The short rates behave like a martingale in regime 2. We also calculate the probabilities that the process will stay in regime 1 and regime 2, and the probability that process will transfer from one state to another and the inference probability for a single date.
From our results, China’s recent interest rate stays in regime 2 in which the interest rate keeps at a low level with a high probability. Interest rate marketization of China will enable market forces to play a greater role in determining the allocation of credit, and economy will be more responsive to changes in rates. The liberalization of rates is a landmark change, and it represents another major milestone in China’s transformation to a market economy.
We acknowledge helpful comments from Chu Zhang, Jiang Luo, Jin Zhang and seminar participants at the Hong Kong University of Science and Technology. The research of this paper has been partially supported by grants from the Fundamental Research Funds for the Central Universities (Project No. 1209022), National Natural Science Foundation of China (Project No. 71303265, No. 71272201 and No. 71231008).
References
- Bandi, F.M. (2002) Short-Term Interest Rate Dynamics: A Spatial Approach. Journal of Financial Economics, 65, 73- 110. http://dx.doi.org/10.1016/S0304-405X(02)00135-6
- Ait-Sahalia, Y. (1996) Testing Continuous-Time Model of the Spot Interest Rate. Review of Financial Studies, 9, 385- 426. http://dx.doi.org/10.1093/rfs/9.2.385
- Stanton, R. (1997) A Nonparametric Model of Term Structure Dynamics and the Market Price of Interest Rate Risk. Journal of Finance, 52, 1973-2002. http://dx.doi.org/10.1111/j.1540-6261.1997.tb02748.x
- Jiang, G.J. and Knight, J.L. (1997) A Nonparametric Approach to the Estimation of Diffusion Processes, with an Ap- plication to a Short Term Interest Rate Model. Econometric Theory, 13, 615-645. http://dx.doi.org/10.1017/S0266466600006101
- Motta, G., Hafner, C.M. and Sachs von, R. (2011) Locally Stationary Factor Models: Identification and Nonparametric Estimation. Econometric Theory, 27, 1279-1319. http://dx.doi.org/10.1017/S0266466611000053
- Florens, J.P. and Simoni, A. (2012) Nonparametric Estimation of an Instrumental Regression: A Quasi-Bayesian Ap- proach Based on Regularized Posterior. Journal of Econometrics, 170, 458-475. http://dx.doi.org/10.1016/j.jeconom.2012.05.016
- Restrepo-Tobn, D. and Kumbhakar, S.C. (2014) Nonparametric Estimation of Returns to Scale Using Input Distance Functions: An Application to Large US Banks. Empirical Economics, 1-26.
- Kristensen, D. (2011) Semi-Nonparametric Estimation and Misspecification Testing of Diffusion Models. Journal of Econometrics, 164, 382-403. http://dx.doi.org/10.1016/j.jeconom.2011.07.001
- Bandi, F.M and Phillips, P.C.B. (2002) Fully Nonparametric Estimation of Scalar Diffusion Models. Econometrica, 71, 241-283. http://dx.doi.org/10.1111/1468-0262.00395
- Bandi, F.M. and Nguyenb, T.H. (2003) On the Functional Estimation of Jump-Diffusion Models. Journal of Econome- trics, 116, 293-328. http://dx.doi.org/10.1016/S0304-4076(03)00110-6
- Johannes, M. (2004) The Statistical and Economic Role of Jumps in Continuous-Time Interest Rate Models. The Journal of Finance, 59, 227-260.
- Hong, Y.M. and Lin, H. (2006) Performance of Discrete-Time Spot Rate Models in China: An Empirical Test on Chi- nese Repo Rates. China Economic Quarterly, 5, 511-532.
- Duffee, G.R. and Stanton, R.H. (2012) Estimation of Dynamic Term Structure Models. The Quarterly Journal of Fi- nance, 2, Article ID: 125008. http://dx.doi.org/10.1142/S2010139212500085
- Siegel, A.F. (2014) Price-Admissibility Conditions for Arbitrage-Free Linear Price Function Models for the Term Structure of Interest Rates. Mathematical Finance, Early View. http://dx.doi.org/10.1111/mafi.12075
- He, D. and Wang, H.L. (2012) Dual-Track Interest Rates and the Conduct of Monetary Policy in China. China Eco- nomic Review, 23, 928-947.
- Harvey, A.C. (1993) Time Series Models. 2nd Edition, MIT Press, Cambridge.
- Cox, J.C., Ingersoll, J.E. and Ross, S.A. (1985) A Theory of the Term Structure of Interest Rates. Econometrica, 53, 363- 384. http://dx.doi.org/10.2307/1911241
- Vasicek, O. (1977) An Equilibrium Characterization of the Term Structure. Journal of Financial Economics, 5, 177- 188. http://dx.doi.org/10.1016/0304-405X(77)90016-2
- Hull, J. and White, A. (1990) Pricing Interest Rate Derivative Securities. The Review of Financial Studies, 3, 573-592. http://dx.doi.org/10.1093/rfs/3.4.573
- Jiang, G.J. (1998) Nonparametric Approach to the Estimation of US Interest Rate Term Structure Dynamics and Im- plications on the Prices of Derivative Securities. Journal of Financial and Quantitative Analysis, 33, 465-497. http://dx.doi.org/10.2307/2331128
- Scott, D.W. (1992) Multivariate Density Estimation: Theory, Practice and Visualization. John Wiley & Sons, Inc., New York. http://dx.doi.org/10.1002/9780470316849
- Chung, K.L. and Williams, R.J. (1990) Introduction to Stochastic Integration. Birkhäuser, Boston.
- Karatzas, I. and Shreve, S.E. (1991) Brownian Motion and Stochastic Calculus. Springer, New York.
- Revuz, D. and Yor, M. (1994) Continuous Martingales and Brownian Motion. 2nd Edition, Springer, New York.
- Hamilton, J.D. (1994) Time Series Analysis. Princeton University Press, Princeton.
- Hamilton, J.D. (1990) Analysis of Time Series Subject to Changes in Regime. Journal of Econometrics, 45, 39-70. http://dx.doi.org/10.1016/0304-4076(90)90093-9
NOTES
*Corresponding author.

























