Journal of Mathematical Finance
Vol.04 No.05(2014), Article ID:51813,4 pages
10.4236/jmf.2014.45030
Interest-Rate Modeling Conundrums
Peter C. L. Lin1,2
1Department of Mathematical Sciences, Financial Engineering Division, Stevens Institute of Technology, Hoboken, USA
2Gamma Paradigm Capital, New York, USA
Email: peter.lin@stevens.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 August 2014; revised 30 September 2014; accepted 11 October 2014
ABSTRACT
The mainstream research in interest-rate modeling has been focusing on a collection of risk tools and pricing formulas which are developed based on the simplified market assumptions and hypotheses. Despite the elegance of the structure, it is noticed that a crucial yet natural factor is missing: the relationship between curve-fitting algorithms and no-arbitrage restrictions on a bond portfolio. Also, the discrepancy between risk-free and default-free bonds is often ignored. This study discusses the modeling conundrums and proposes a framework based on the preferred- habitat hypothesis for advanced term-structure construction that overcomes these limitations in current models. This article serves as an introduction for future work.
Keywords:
Interest-Rate Models, Preferred-Habitat Hypothesis, No-Arbitrage Conditions, Curve-Fitting Algorithms, Bond Portfolios

1. Introduction
The expectations hypothesis proposed by Fisher [1] assumes that zero-coupon bonds of different maturities are perfect substitutes. In general, equilibrium risk-free interest-rate models are based on the expectations hypo- thesis though the hypothesis comes in three forms:
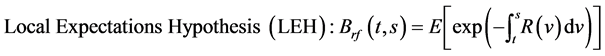 (1)
(1)
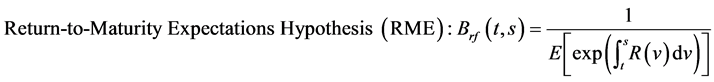 (2)
(2)
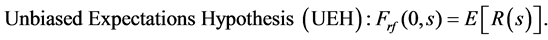 (3)
(3)
Here 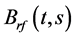 denotes the risk-free zero-coupon bond at time
denotes the risk-free zero-coupon bond at time 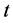 with maturity time
with maturity time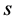 , and
, and  denotes risk-free instantaneous forward curve at time
denotes risk-free instantaneous forward curve at time  with term (time-to-maturity)
with term (time-to-maturity)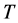 . Consequently, the short-rate process
. Consequently, the short-rate process  is equivalent to
is equivalent to . The expectation
. The expectation 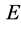 is taken under the real-world measure
is taken under the real-world measure . Following from the arbitrage-free condition from Harrison and Pliska [2] , the equality from (1) indicates a risk-neutral world where risk premium is zero, and the risk-neutral measure
. Following from the arbitrage-free condition from Harrison and Pliska [2] , the equality from (1) indicates a risk-neutral world where risk premium is zero, and the risk-neutral measure 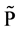 and the real-world measure
and the real-world measure 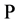 coincide. The equality from (3) indicates a risk-neutral world where risk premium is zero when the numeraire is
coincide. The equality from (3) indicates a risk-neutral world where risk premium is zero when the numeraire is 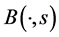 instead of a money market account1, and the forward risk-neutral measure
instead of a money market account1, and the forward risk-neutral measure 

The LEH and RME hypotheses are exclusive unless the short rate is deterministic. The LEH and UEH are exclusive when risk-free bonds are not tradable asset which is the asset with zero volatilities2. This study proposes a no-arbitrage framework that is consistent with the three expectations hypotheses. Then, based on the risk-free interest-rate modeling framework, default-free bonds3 are included to represent a form of tradable asset that is characterized in relation to risk-free bonds.
When buying and holding a default-free bond until its maturity, the return is risk-free, and the yield should equal to the risk-free return over the same investment horizon. Nonetheless, unlike risk-free bonds, default-free bonds are tradable and are affected by the supply and demand of the buyers and sellers. If we may borrow the term, convenience yield, from a commodity for representing the benefit of holding physical assets while quanti- fying supply-and-demand factor, the distinction between risk-free and default-free bonds can be described in the same fashion by introducing a term structure of “inconvenience yield” on the default-free bond. In accordance to the preferred-habitat hypothesis, this inconvenience is an analogy of the trading restrictions of arbitrages and the supply-and-demand factor of different maturity bonds.
The preferred-habitat hypothesis proposed by Culbertson [5] and Modigliani and Sutch [6] assumes that bonds of different maturities are close substitutes but not perfect. The hypothesis separates an interest-rate curve into two paradigms consisting of the expectations hypothesis and the market-segmentation hypothesis. As the expectations hypothesis states, this part of the curve is driven by arbitrageurs who take advantage of price dis- crepancy between bond with different maturities. On the other hand, the market-segmentation hypothesis asserts the existence of preferred-habitat investors who seek only bonds with specific maturities. Consequently, the preferred-habitat investors contribute the term-specific idiosyncratic risk and supply-and-demand effect. The aggregated effect from the market-segmentation hypothesis is called liquidity premium. This study proposes a new modeling framework based on the preferred-habitat hypothesis in which the liquidity premium is quantified endogenously and is linked to the inconvenience yield consistently under empirical practice between curve-fit- ting and bond portfolios.
A curve-fitting algorithm reduces the possible infinite-dimensional market model to a factor model with few sources of randomness. Sometimes the algorithm associated with a curve is pre-defined. For example, the High-Quality-Corporate Bond Yield curve proposed by US Treasury, which is used to discount the corporate pension liability, follows specific steps to construct. In other cases, industries pick the common algorithms like Nelson-Segal method or the quasi-cubic Hermite spline method for statistical or computational reasons. None- theless, fitted curve dynamics under the empirical measure usually admit arbitrages due to simplified assump- tion from the expectations hypothesis. In other words, if the market only follows an assumption without market segmentation, then the Heath-Jarrow-Morton framework restricts the curve factor loadings to be exponential splines. Detailed discussion can be found in Filipovic [7] .
In order to resolve the no-arbitrage dynamics of a fitted curve, one shall examine the difference of a fitted curve and the bond portfolio the curve is fitted to. Based on the preferred-habitat hypothesis, term-specific idio- syncratic risk is added to a bond portfolio under the restriction that the idiosyncratic risk vanishes after applying a curve-fitting algorithm. Consequently, this more general framework will allow the use of any deterministic curve-fitting algorithm while guaranteeing the absent of arbitrages.
The interest-rate modeling conundrums then consist of three parts. First, a new no-arbitrage framework is needed to unify the expectations hypotheses under the preferred-habitat market assumption. Second, a connec- tion needs be established between any deterministic curve-fitting algorithm and no-arbitrage restrictions when incorporating the preferred-habitat market assumption. Third, it requires to provide a detailed implementation of an interest-rate model that satisfies the proposed framework. The last part is left for future study.
2. A New Modeling Framework
Recent research shows that no-arbitrage models do not capture supply and demand in the Treasury bond market. Krishnamurthy and Vissing-Jorgensen [8] showed that changes in Treasury supply have large effects on a va- riety of yield curve movements. Though their research focused on the spread between corporate and Treasury bonds, the result can be further applied to connect the money market account to the bond market. Furthermore, Duffee [9] exposed the idiosyncratic risk in short-term Treasury bills and postulated that this risk was the con- sequence of the time-variation of the inconvenience yield for holding Treasury bills. Concurrent research con- ducted by Duffie [10] showed similar idiosyncratic supply and demand for different maturities in the repo mar- ket. Moreover, we expect a similar result between deliverable Treasury bonds and Treasury bond futures. Here the cheapest-to-deliver option may affect bond market equilibrium through an imbalance of supply and demand in different maturities. In this section a new model framework is proposed by first focusing on the risk-free and default-free no-arbitrage model, then introducing the criteria for the no-arbitrage general term-structure models.
The gap between theoretical research in term-structure modeling and portfolio management is caused by the construction of the curves. In practice, a term structure is generally used to represent the market movements of a portfolio. For example, the US Treasury bond yield curve represents the portfolio consists of US Treasury bill, notes, and bonds. Many research have devoted to find the major factors in curve movement with respective to specific portfolios. When the portfolio is not dramatically variated, it is likely to identify few major components to characterize the portfolio. The technique is no different to a dimension reduction procedure. However, the model might be too simplified to capture any significant idiosyncratic risk. As a result, we propose a framework of a term-structure model by combining the conventional term-structure model paradigm and the random field.
Let 




where 


where 


Risk-Free vs Default-Free
The first conundrum we shall discuss in fundamental term-structure modeling is to distinguish the risk-free and default-free curves. Though most literature treat the two curves indifferently with a reason that buying and holding a default-free asset creates a risk-free return, risk-free and default-free assets bear very different mean- ings since only the latter are tradeable. The HJM framework [11] provides a hint for improvement. First, by definition in [12] , risk-free assets need to have zero volatility; hence it is necessary that 




Consequently the HJM framework asserts that drift term of the curve process must also be zero. Hence we have the following no-arbitrage condition:
No-Arbitrage Condition 1. A risk-free curve 


Since

Also, since the default probability approach zero when


No-Arbitrage Condition 2. A default-free curve 

Unlike risk-free bonds, tradable default-free bonds are exempted from the zero-volatility constraint, yet the potential arbitrage might exist between buying-and-holding a default-free bond and a risk-free bond. Instead of applying an exogenous term structure of inconvenience yield to model the liquidity premium between two investments, we will quantify inconvenience yields endogenously based on a no-arbitrage condition between curve-fitting algorithms and bond portfolios. Let 
No-Arbitrage Condition 3. Given a deterministic curve-fitting algorithm

Lemma 1. A sufficient condition for a default-free interest-rate curve satisfying No-Arbitrage Conditions 1-3 is

Proof. Given the default-free term structure and the diffusion term

where 

which shows that the expected bond price with maturity 






Equation (9) is a natural extension from the bond-curve relationship in Equation (11). Hence, a term-structure model and its curve-fitting algorithm are unified. From Equations (11) and (12) and by rolling over ready-to- mature default-free bonds we then have

which shows that the liquidity premium implied by the default-free bonds represents a term structure of inconvenience yield. Hence, the no-arbitrage constraint between curve-fitting algorithms and bond portfolios is consistent with the preferred-habitat hypothesis from which term-specific spot inconvenience yields are com- puted endogenously.
3. Conclusions
In this study, a new no-arbitrage term-structure framework is proposed to overcome the no-arbitrage conun- drums in interest-rate modeling. Incorporating the preferred-habitat hypothesis with term-specific idiosyncratic risk associated with default-free bonds, a no-arbitrage connection between curve-fitting algorithms and bond portfolios is established. Then, the term structure of inconvenience yield is introduced and quantified endoge- nously to unify the risk-free and the default-free bonds. This framework further shows consistency between the supply-and-demand factor and the spot inconvenience yield and links back to traditional no-arbitrage para- digm.
This article serves as an introduction for future research. The next step will be implementing an interest-rate model that satisfies the proposed no-arbitrage conditions. Applications in either interest-rate forecasting or derivatives pricing can further test the robustness of the framework.
References
- Fisher, I. (1930) The Theory of Interest. Macmillan, New York.
- Harrison, J.M. and Pliska, S.R. (1981) Martingales and Stochastic Integrals in the Theory of Continuous Trading. Stochastic Processes and Their Applications, 11, 215-260. http://dx.doi.org/10.1016/0304-4149(81)90026-0
- Geman, H., El Karoui, N. and Rochet, J.-C. (1995) Changes of Numéraire, Changes of Probability Measure and Option Pricing. Journal of Applied Probability, 32, 443-458. http://dx.doi.org/10.2307/3215299
- Jarrow, R.A. (2009) The Term Structure of Interest Rates. Annual Review of Financial Economics, 2, 69-96. http://dx.doi.org/10.1146/annurev.financial.050808.114513
- Culbertson, J. (1957) The Term Structure of Interest Rates. Quarterly Journal of Economics, 71, 485-517. http://dx.doi.org/10.2307/1885708
- Modigliani, F. and Sutch, R. (1966) Innovations in Interest-Rate Policy. Interest-Rate Policy. American Economic Review, 56, 178-197.
- Filipovic, D. (2001) Consistency Problems for Heath-Jarrow-Morton Interest Rate Models. Springer, Berlin. http://dx.doi.org/10.1007/b76888
- Krishnamurthy, A. and Vissing-Jorgensen, A. (2010) The Aggregate Demand for Treasury Debt. Working Paper.
- Duffee, G.R. (1996) Idiosyncratic Variation of Treasury Bill Yields. Journal of Finance, 51, 527-551. http://dx.doi.org/10.1111/j.1540-6261.1996.tb02693.x
- Duffee, G.R. (1996) Special Repo Rates. Journal of Finance, 51, 493-526. http://dx.doi.org/10.1111/j.1540-6261.1996.tb02692.x
- Heath, D., Jarrow, R. and Morton, A. (1992) Bond Pricing and the Term Structure of Interest Rates: A New Methodology for Contingent Claims Valuation. Econometrica, 60, 77-105. http://dx.doi.org/10.2307/2951677
- Björk, T. (2009) Arbitrage Theory in Continuous Time. 3rd Edition, Oxford.
NOTES
1For the definition of numeraire and forward risk-neutral measure, please refer to [3] .
2More detailed discussion can be found in Jarrow [4] .
3The US Treasury bonds are often taken as proxy of default-free bonds.


