Journal of Mathematical Finance
Vol.4 No.4(2014), Article
ID:48837,4
pages
DOI:10.4236/jmf.2014.44021
Solution of Stochastic Non-Homogeneous Linear First-Order Difference Equations
Seifedine Kadry1*, Abdelkhalak El Hami2
1American University of the Middle East, Egaila, Kuwait
2LOFIMS Laboratory, INSA de Rouen, Rouen, France
Email: *skadry@gmail.com, abdelkhalak.elhami@insa-rouen.fr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 May 2014; revised 30 June 2014; accepted 13 July 2014
ABSTRACT
In this paper, the closed form solution of the non-homogeneous linear first-order difference equation is given. The studied equation is in the form: xn = x0 + bn, where the initial value x0 and b, are random variables.
Keywords:Stochastic Linear Difference Equations, Random Variables, Closed Form Solution, Direct Transformation Technique

1. Introduction
A difference equation or dynamical system describes the evolution of some variable over time. The value of this variable in period t is denoted by xn. The time index n takes on discrete values and typically runs over all integer numbers Z, e.g. t = ×××, −2, −1, 0, 1, 2,×××. By interpreting t as the time index, we have automatically introduced the notion of past, present and future [1] .
Many problems in Probability give rise to difference equations. Difference equations relate to differential equations as discrete mathematics relates to continuous mathematics. Anyone who has made a study of differential equations will know that even supposedly elementary examples can be hard to solve. By contrast, elementary difference equations are relatively easy to deal with.
Aside from Probability, Computer Scientists take an interest in difference equations for a number of reasons. For example, difference equations frequently arise while determining the cost of an algorithm in big-O notation [2] . In engineering, difference equations arise in control engineering, digital signal processing, electrical networks, etc. In social sciences, difference equations arise to study the national income of a country and then its variation with time, Cobweb phenomenon in economics [3] , etc. Similar to differential equation, difference equation is the most powerful instrument for the treatment of discrete processes.
Stochastic difference equations are difference equations with random parameters. Such equations arise in various disciplines, for example economics [4] , physics, nuclear technology, biology and sociology. In this paper, we present a new technique based on the direct transformation technique to express analytically the probability density function of the general solution of stochastic linear 1st order difference equations.
2. Linear 1st Order Difference Equations
A typical linear non-homogeneous first order difference equation is given by:
 (1)
(1)
where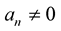 ,
,
![]() and
and
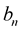 are real-valued functions. The unique solution of (1) may be found as follows:
are real-valued functions. The unique solution of (1) may be found as follows:
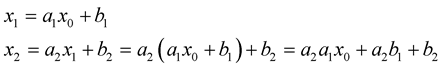
Now by induction, we can show:
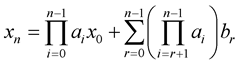 (2)
(2)
To establish this, assume that (2) holds for order n. Then from (1)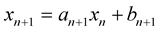 , hence (2) gives:
, hence (2) gives:
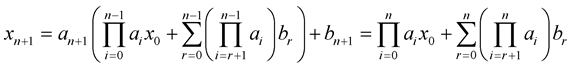
Thus (2) holds for all![]() .
.
There is a special case of (1) that is important in many engineering and business applications, is given by:
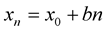 (3)
(3)
This case is studied throughout this paper where x0 and b, are random variables.
3. Direct Transformation Technique
There are several versions of the Direct Transformation Technique in the literature [5] -[9] ; we will provide a simple one for 1-dimension variable then for N-dimension variables.
1-dimension variable Let X be a continuous random variable with probability density function (pdf),
![]() and defined over an interval I. Let g:
and defined over an interval I. Let g:
![]() be a continuous one-to-one function, i.e. its inverse h:
be a continuous one-to-one function, i.e. its inverse h:![]()
![]() . Let Y = g(X), then the probability density function of Y,
. Let Y = g(X), then the probability density function of Y,
![]() is given by:
is given by:
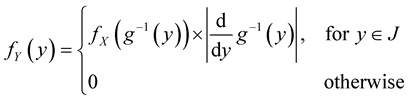 (4)
(4)
Example: X has probability density function given by
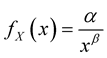 (where x, α, and β are strictly positive real numbers). Let
(where x, α, and β are strictly positive real numbers). Let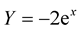 , we want to find the probability density function of Y,
, we want to find the probability density function of Y,![]() . Here
. Here![]() ,
,![]() . Using (4), we have:
. Using (4), we have:
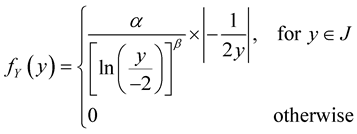 .
.
N-dimension variables Let
![]() n continuous random variable with given joint probability density function
n continuous random variable with given joint probability density function
![]() . Consider a one-to-one transformation function
. Consider a one-to-one transformation function
![]() where
where
![]() is continuous with respect to every variable and its partial derivatives is continuous as well. Then the joint probability density function of
is continuous with respect to every variable and its partial derivatives is continuous as well. Then the joint probability density function of
![]() is given by:
is given by:
 . (5)
. (5)
4. Application
In this section, we will solve the stochastic difference equation
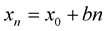 (given in (3)), where
(given in (3)), where
![]() and
and
![]() are random variables with the known joint probability density function, by finding the probability density function of
are random variables with the known joint probability density function, by finding the probability density function of
![]() using (5). So in this stochastic difference equation we have two random variables (
using (5). So in this stochastic difference equation we have two random variables (![]() ,
,![]() ) as input and one random variable
) as input and one random variable
![]() as output. For example, let
as output. For example, let![]() . By using (5), let
. By using (5), let
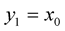 and
and
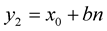 with inverse
with inverse
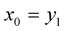 and
and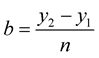 . The joint probability density function of
. The joint probability density function of
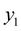 and
and
![]() (Figure 1) is given by:
(Figure 1) is given by:
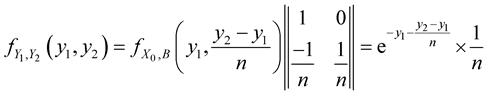 .
.
Now to find the probability density function of![]() , i.e.
, i.e.
![]() we must find the marginal probability density function of Y2 (Figure 2) by integrating out of Y1:
we must find the marginal probability density function of Y2 (Figure 2) by integrating out of Y1:

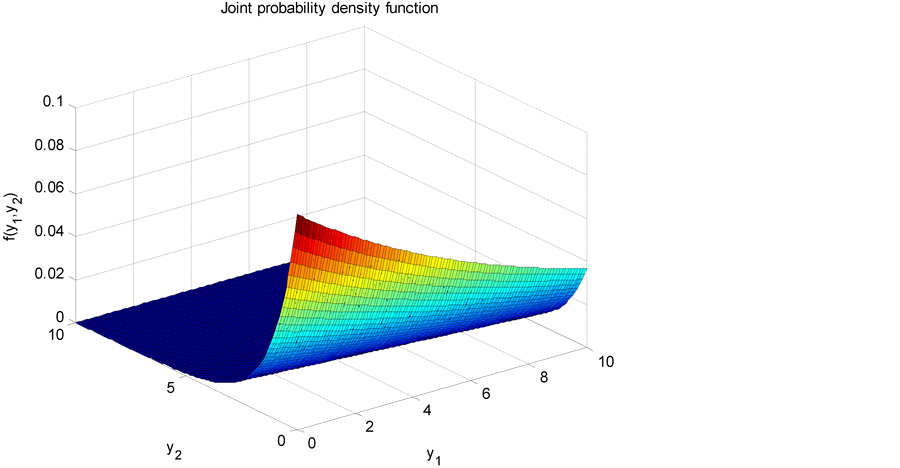
Figure 1. Joint probability density function of y1 and y2.
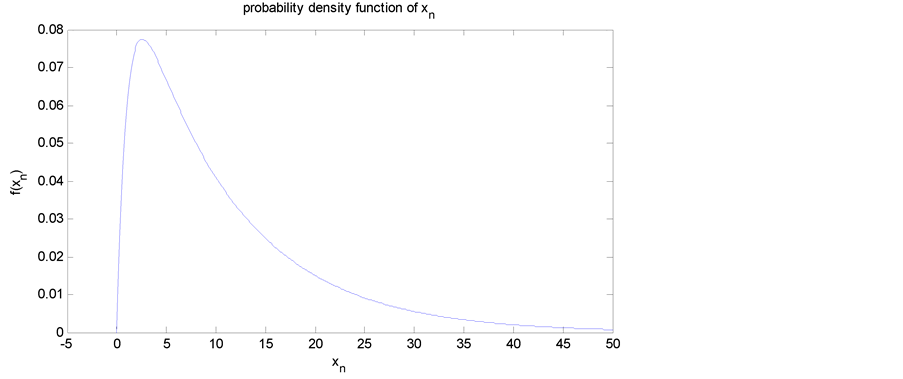
Figure 2. Probability density function of xn.
We can show easily that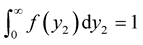 .
.
References
- Elaydi, S. (2004) An Introduction to Difference Equations. 3rd Edition, Springer-Verlag, New York.
- King, F. (2005) Difference Equations [PDF Document]. Retrieved from Lecture Notes Online Web Site: http://www.cl.cam.ac.uk/teaching/2004/Probability/
- Chui, C.K. and Chen, G. (1987) Kalman Filtering with Real-Time Applications. 2nd Edition, Springer-Verlag, New York. http://dx.doi.org/10.1007/978-3-662-02508-6
- Novak, S.Y. (2011) Extreme Value Methods with Applications to Finance. Chapman & Hall/CRC Press, London. http://dx.doi.org/10.1201/b11537
- Soong, T.T. (1973) Random Differential Equations in Science and Engineering. Academic Press, New York.
- Kadry, S.A. (2007) Solution of Linear Stochastic Differential Equation. USA: WSEAS Transactions on Mathematics, April 2007, 618.
- Kadry, S. (2012) Exact Solution of the Stochastic System of Difference Equations. Journal of Mathematical Control Science and Applications (JMCSA), 5, 67-70.
- Kadry, S. and Younes, R. (2005) étude Probabiliste d’un Système Mécanique à Paramètres Incertains par une Technique Basée sur la Méthode de transformation. Proceedings of the 20th Canadian Congress of Applied Mechanics (CANCAM’ 05), Montreal, 30 May, 490-491.
- Kadry, S. (2012) Probabilistic Solution of Rational Difference Equations System with Random Parameters. ISRN Applied Mathematics, 2012, Article ID: 290186. http://dx.doi.org/10.5402/2012/290186
NOTES

*Corresponding author.

