Journal of Mathematical Finance
Vol.4 No.1(2014), Article ID:42220,14 pages DOI:10.4236/jmf.2014.41003
Catastrophe Risk Derivatives: A New Approach
Graduate school of Economics, Osaka University, Osaka, Japan
Email: bekralasmhd@gmail.com
Received November 7, 2013; revised December 8, 2013; accepted December 29, 2013
ABSTRACT
The multiplication of disasters during the last two decades beside the urbanism expansion has made catastrophe claims grow dramatically. Against a priced reinsurance, catastrophe derivative products became ever more attractive to insurance companies. A robust pricing of these derivatives is based on an appropriate modeling of the loss index. The current study proposes a unique model that takes into account the statistical characteristics of the loss amount’s tails to assess its real distribution. Thus, unlike previous models, we elaborately do not make any assumption regarding the probability of jump sizes to facilitate the calculation of the option price but deduct it instead of using Extreme Value Theory. The core of our model is a jump process that allows later for loss amounts’ re-estimation. Using both the Esscher transform and the martingale approach, we present the price of a call option on the loss index in a closed form. Finally, to confirm the underpinning theory of the model, numerical examples are presented as well as an algorithm that can be used to derive the option prices in real time.
Keywords:Compound Poisson Process; Extreme Value Theory; Esscher Transform; Index Correction
1. Introduction
Cities are currently in a constant expansion. The modernization and the use of technology in urban and rural areas require more and more investments and expenses. This proliferation is driving the expected value of the catastrophe to attain important sums, which makes it nowadays very hard for an insurance company to cover these costs. For instance, a big earthquake in Tokyo could engender a higher cost than the capitalization of all the Japanese insurance companies. To deal with this matter, insurance companies used reinsurance techniques during the past years. They could thus assure a part of the catastrophe claim and pay premiums to other companies against the coverage of the non-supported insurance part. These premiums became more expensive as the assured goods became costly and the catastrophe occurrence became more frequent. One of the solutions to this problem is to drag the cash from financial market since this candidate has a huge liquidity potential compared with the claim amounts. The key that can open the doors to the stock exchange for catastrophe risk hedging seekers would be the securitization of their catastrophe risk.
From their apparition in the CBOT (Chicago Board of Treading) in 1995, the catastrophe derivatives were known as an incomparable success. Therefore, on the other hand, the financial literacy is giving an increasing interest to the modeling of these new derivatives.
A shared point among all the catastrophe products is their underlying common that is an index representing the amount engendered by some disasters during a certain period of time. This index has been created to solve a moral hazard problem since the veracity of the catastrophe amounts was not observable by investors from the financial statement of an insurance company.
A good catastrophe derivative pricing passes inevitably through a good modeling of the loss index. Catastrophe Loss indexes display the value of the insurance claims that surpasses a certain amount. That is because the insurance institutions are interested only in the large amounts (the extraordinary claims) as the small ones are covered by the reserve made for this purpose. For instance, the most common Loss index: the PCS index when created, took into account only the amounts above $5 million and nowadays this floor has moved to $25 million1.
By observing these loss indexes, we see that the occurrence of these claims seems to follow a jump process as the extra claim amount is generated by catastrophic events that have a random occurrence and size. Thus some authors like Cox, Fairchild and Pederson [1] modeled the index as a mixture of a Poisson process and a Brownian motion. Geman and Yor [2] and Muerman [3] proposed a jump diffusion model with a fixed amplitude of the events’ effects. The inconvenience with these approaches is that they don’t differentiate between the catastrophes’ impacts as they assign the same size to all claims, while in reality different catastrophes in an interval of time cause different claim amounts, and thus different jump sizes on the Loss Index.
To overcome this lack, Jaimungal [4] among others used a Compound Poisson Process (CPP) without specifying the distribution of the jump sizes. His work led to a complicated pricing formula that required many iterations to be solved. Others like Dasios and Jang [5] took the jump size as an exponentially distributed random variable. It can be proved by using the Extreme Value Theory that this assumption is not appropriate for the catastrophe data. Whereas, Duan and Yu [6] supposed that these jumps flowed a lognormal distribution so that they could create a short cut to the Merton model since with other distributions the prices’ stochastic differential equation (SDE) didn’t have a known closed solution. A very helpful assumption, cert, however, is unfortunately not based on any evidence.
Unlike the previous researches, we do not attribute any probability distribution to the claims size but will instead try to deduce it by using some useful statistical tools, as we lack of data. Also, to derive our non-arbitrage price, we will first use an Esscher transform approach instead of the classic Martingale approach proposed on other papers like in Fujita Takahiko et al. [7]. Our general goal is to provide a closed form pricing that can be used easily in practice, which doesn’t request many calculations nor involves hard computations.
The general methodology of this paper will be as follows: Section 2 introduces the skeleton of the model and derives the jump size distribution. The next section uses the Esscher transform to assess the catastrophe option price. Section 4 adds a claim correction process and estimates the previous option price by the Martingale approach besides the Esscher method. The pricing during the development period is given in Section 5. Section 6 proposes an efficient algorithm to compute our derivatives’ value in practice. Section 6 concludes the paper.
2. Modeling the Loss Index
This section is dedicated to the modeling of the underlying of the catastrophe products: the Loss Index. One of the most famous and pioneer indexes known in the market is the PCS index. We will later observe its general behavior to model our underlying.
2.1. General Framework
First, denote by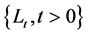 , the Loss index process. Let
, the Loss index process. Let 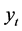 be a random variable representing the claim amounts shown by the index at time t. As usual we set
be a random variable representing the claim amounts shown by the index at time t. As usual we set  as our probability space with the statistical probability measure
as our probability space with the statistical probability measure 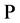 (real world probability measure).
(real world probability measure).
Following the existing PCS index, the Loss process is divided into two distinguished periods applicable to the options it proposes:
A loss period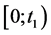 : where
: where 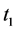 represents the first maturity of the option. That is for a European call option for example, at the end of this period the index’s level should be higher than the strike so that the option would have an eventual payoff. This pay off if in contrast with plain vanilla products, would be done after the second period.
represents the first maturity of the option. That is for a European call option for example, at the end of this period the index’s level should be higher than the strike so that the option would have an eventual payoff. This pay off if in contrast with plain vanilla products, would be done after the second period.
A development period : since the real amount engendered by a sinister cannot be assessed in the spot, a period is left for the option investor so that the index shows the exact amount of the claims due by the catastrophes happening between
: since the real amount engendered by a sinister cannot be assessed in the spot, a period is left for the option investor so that the index shows the exact amount of the claims due by the catastrophes happening between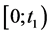 . This time lag will let the experts estimate all the damage caused by the previews events. This is beneficial for the insurance company as its due claims wouldn’t be underestimated. Note that only the re-estimations of the catastrophe sinister that happened during the loss period are taken into account. Catastrophes that occur between
. This time lag will let the experts estimate all the damage caused by the previews events. This is beneficial for the insurance company as its due claims wouldn’t be underestimated. Note that only the re-estimations of the catastrophe sinister that happened during the loss period are taken into account. Catastrophes that occur between  are not considered as the option would have reached its maturity after
are not considered as the option would have reached its maturity after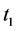 . In case the option was in the money by
. In case the option was in the money by  the payoff will occur at
the payoff will occur at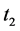 .
.
For simplicity we will start by modeling the loss period and price the option within that interval. Later we will include the development period once some of our useful results are derived.
If we compare the damages caused by different catastrophe events, we would notice that their sizes varies. Also, their occurrence seems to be random2. The PCS index for instance, shows some jumps happening randomly along the time axis. Therefore following Jaimungal et al. [4], we model the Loss index as below:

 (1)
(1)
Where 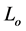 is the current Loss Index position and
is the current Loss Index position and  an adapted stochastic process (a CPP) satisfying the usual smoothing conditions, such as:
an adapted stochastic process (a CPP) satisfying the usual smoothing conditions, such as:
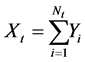 (2)
(2)
 represents the number of catastrophes occurring up to but not including the time t. Hence the sum
represents the number of catastrophes occurring up to but not including the time t. Hence the sum 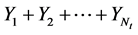 is the total amount of the claims (over the threshold) to be hedged by the institution. Here we are making no assumption regarding the distribution of the catastrophe claim amounts (i.e. size of the jump). Our only hypothesis is the classical i.i.d. assumption3.
is the total amount of the claims (over the threshold) to be hedged by the institution. Here we are making no assumption regarding the distribution of the catastrophe claim amounts (i.e. size of the jump). Our only hypothesis is the classical i.i.d. assumption3.
 symbolizes the filtration generated by the CPP
symbolizes the filtration generated by the CPP  and the
and the  null set of
null set of  and we write:
and we write:  .
.
Now that our model skeleton is settled we will next derive the probability distribution of the jump sizes.
2.2. A distribution for the Claim Amounts
In this subsection we will deduct the distribution of the amounts that are measured by the index starting from the sample of all the observable claims by using some statistical approaches.
Some scientific evidences show that the occurrence of an earthquake opens a hole in the earth. The opening of the hole may be done by a series of other earthquakes. This event is followed by the hole’s closing process, done via another set of earthquakes. If the original earthquake has a big magnitude then the following provoked ones (the replicas) have an important occurrence probability. This is to say that one big earthquake can generate many others. This doesn’t come in contrast with our i.i.d. assumption on the jump sizes since we are stating here that the “occurrence of the jumps” is dependent whereas the amplitudes stay independent. Add that to the fact that the Index takes into consideration many disasters not only earthquakes, thus disasters sizes are independent as their source might be different. For instance Hurricanes claim sizes are different from earthquake ones. So the probability of having many magnitude picks (and thus values that are measured by the index) during an interval 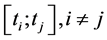 with
with  the time of a catastrophe event manifestation (a big jump occurrence), is high. This observation is important in the sense that statistically it allows us to use the strong law of large numbers.
the time of a catastrophe event manifestation (a big jump occurrence), is high. This observation is important in the sense that statistically it allows us to use the strong law of large numbers.
Since we are dealing only with high amounts claims it is more appropriate to search for the claim’s tail distribution rather than using all the observations. Hence, the Extreme Value Theory (EVT)4 that treats this subject seems to offer some useful tools for our quest.
According to this theory, the distribution of the tail depends on our definition of a high value. The First definition that we would carry along this paper, also called the Block Maxima, defines the extreme values of a data set obtained during an interval say : as the set of the maximum amounts of each subset
: as the set of the maximum amounts of each subset 
 . In other words relying on this definition the high values are defined to be the set that contains the maximum points of each time subset. The way the division of the time axis into subset is arbitrary.
. In other words relying on this definition the high values are defined to be the set that contains the maximum points of each time subset. The way the division of the time axis into subset is arbitrary.
Let . According to the Fisher, Tippet and Gnedenko Theorem of the block maxima if there exists a couple
. According to the Fisher, Tippet and Gnedenko Theorem of the block maxima if there exists a couple 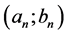 where
where  and
and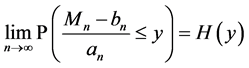 , with H a nondegenerate function; then: H has a Generalized Extreme Value (GEV) distribution which is a general representation of the following distributions: Weibull, Fréchet and of the Gumbel law. Which infers that our jump size variable that is represented by the maxima of the claims’ data, has the same distribution as H with different parameters. In other words the normalized maximum has only one of the distributions stated above. Recall that GEV CDF is:
, with H a nondegenerate function; then: H has a Generalized Extreme Value (GEV) distribution which is a general representation of the following distributions: Weibull, Fréchet and of the Gumbel law. Which infers that our jump size variable that is represented by the maxima of the claims’ data, has the same distribution as H with different parameters. In other words the normalized maximum has only one of the distributions stated above. Recall that GEV CDF is:
 (3)
(3)
We now possess a general idea on how the probability distribution of our loss index could be. In the next subsection we will deduct which one of the tree probabilities could be a robust presentation of our claims.
2.3. Selection of the GEV Distribution
To assess which one of the former distributions fits the catastrophe claims, a logical approach would be to make the claims data undergo some statistical tests. However, this data set is not available for the public which complicates our task.
Nevertheless, using some catastrophe claim known characteristics, we know that a right skewed distribution would not be appropriate since it infers that the catastrophic amounts are concentrated near by the tail of the regular distribution, which means that the catastrophe damages have a tiny probability to be considerably pricier than the regular sinister claims, which is not the case in reality where disaster claims are much higher than the normal ones. A left skewed density instead says that very high amounts have more occurring probability while the amounts near the tail have a really tiny chance to happen. Also it allows to the claims that are to be too far from the original tail to be more probable, while we know that the damage function should be bonded as the parts covered by a catastrophe insurance are not unlimited. Thus, an appropriate distribution should be between the two previews extreme cases so with skew close more or less close to zero. So, the next step would be to assess the skewness of to choose the accurate distribution.
To do so, we used Fraga Alves [10] results stating that the skewness of a GEV in function of its parameter . The skewness of the G.E.V. distribution is positive for
. The skewness of the G.E.V. distribution is positive for  > −2.8, negative for
> −2.8, negative for 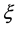 < −2.8 and approximately equal to 1.14 for
< −2.8 and approximately equal to 1.14 for 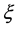 = 0.
= 0.
On the other hand the G.E.V. corresponds to the Fréchet distribution for  > 0, to the Weibull one in the case
> 0, to the Weibull one in the case 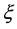 < 0 and finally it represents the Gumbel law when
< 0 and finally it represents the Gumbel law when 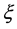 = 0.
= 0.
We deduct that the Fréchet distribution is more likely to be right skewed. Modeling the extreme values by a Fréchet distribution is equivalent to suppose that the maximum amounts are too close from the damages usually caused whereas in reality these values are not concentrated near by the tail area.
By the same reasoning, the Weibull distribution assigns a large probability to the values that are situated too far from the end of the original distribution of the claims, and presents some times infinite tails (no boundaries). This seems to be unrealistic since the earthquakes wave vanishes after a certain distance and also because the insurance coverage is also limited as stated before.
Contrariwise the Gumbel law offers a certain uniformity in its distribution. It is slightly asymmetric and have a finite tail. In its attraction domain, data that are neither far nor too close from the usual claim amounts are affected with higher probability, which seems to be case of the extraordinary catastrophe events. Taking all the previous into account, we made the Gumbel distribution our choice between the three distributions for claim’s extreme values modeling. Note that the Gumbel distribution, is widely used in many fields where extreme values dealt with, as mentions Isabael Fraga [9]. Some extreme cases of the two other distributions, may feet the catastrophe data, but since we do not dispose of the catastrophe data this fact is less probable and unverifiable, we do not take it into consideration in our current research. As a reminder the Gumbel CDF and PDF are defined consecutively as bellow5, for :
:
 (4)
(4)
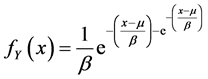 (5)
(5)
Its expectation is given by:
 (6)
(6)
Where 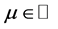 is the location parameter,
is the location parameter,  represents the scale parameter and
represents the scale parameter and 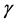 is the Euler-Mascheroni constant.
is the Euler-Mascheroni constant.
In practice if catastrophe data is available we suggest that the above parameters assessment is done by the Moment Method (MM) instead of the Maximum likelihood (ML). Because even though the latest is easier to derive, it leads to a more complicated equation than the one resulted from the MM and could yield to a biased estimation6. The calibration with the MM gives:
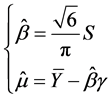 (7)
(7)
Where  and
and  represent the average and the variance of our catastrophe historical data sample. These are the only statistics needed to construct all our jump size law.
represent the average and the variance of our catastrophe historical data sample. These are the only statistics needed to construct all our jump size law.
To sum up, we started from the fact that only the extraordinary events are accounted for in the Loss Index. We used the EVT to extract the probability distribution of the jump size as data was unavailable to be tested statistically. In practice, the average amount of catastrophe claims and its second moment are available information for insurance institutions, even if the company might not possess all the historical data. Therefore, one can know the jump size distribution with all its parameters and all its moments only by solving Equation (7). Now that we have a probability distribution for our catastrophic claims’ size, we can start to derive our option pricing formula.
3. Catastrophe Option Pricing
At this point we are trying to calculate an option price, on an index which is modeled by an exponential CPP. This makes the Esscher transformation procedures applicable to derive our option price7. We will hereafter consider only the case of a call option as the put option value can be derived via the putt-call parity, once we know the call’s value. Our first step is to calculate the moment generating function of our stochastic process component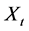 .
.
3.1. 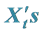 Moment Generating Function
Moment Generating Function
For the pricing purpose, we will apply a concept widely used in actuaries called the Esscher transform that was introduced by Esscher [13]. As the other transforms -for instance, the Fourier transformthis function takes a defined function to another space where some operations become available and/or easier. Traditionally the Esscher transform was used to shift the mean of a PDF. Lately this use is not restricted to random variables only but also for stochastic process. Before we deduct our option price, let us define some useful concepts.
If we note  and
and  the PDF and CDF of our stochastic process
the PDF and CDF of our stochastic process  consecutively, then the Esscher transform function could be defined as follow:
consecutively, then the Esscher transform function could be defined as follow:
 (8)
(8)
If the CDF is not necessarily differentiable then we define it as:
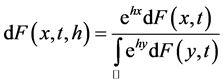 (9)
(9)
Let z be a real number. Define ’s Moment Generating Function MGF as:
’s Moment Generating Function MGF as:
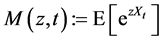 (10)
(10)
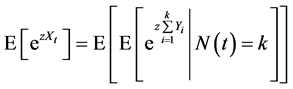 (11)
(11)
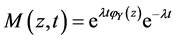 (12)
(12)
 (13)
(13)
The passage from (9) to (11) is allowed because of our i.i.d. assumption on the variables .
.  is
is  MGF. We used after that Taylor expansion results to get to the final equation.
MGF. We used after that Taylor expansion results to get to the final equation.
3.2. Esscher Option Pricing
Before extracting our price we have to add some assumptions concerning the market.
1) The non-existence of transaction costs nor taxes 2) The absence of arbitrage 3) There exists a riskless interest rate noted δ that we suppose static for simplicity purpose.
We are in the presence of one source of randomness (the CPP) and one asset. Therefore, according to the Meta Theorem (and since we imposed the non-arbitrage condition to our model) the price of our option is unique. Recall that the Esscher Moment generating function is defined as follow:
 (14)
(14)
 (15)
(15)
The Esscher transform shifts the whole probability distribution of a stochastic process. Our goal then is to move our distribution so that the resulted probability measure is a martingale. This would be the case if the Equation (14) below is satisfied:
 (16)
(16)
The left hand side is the Moment generating function of the shifted exponential CPP distribution. The last equation leads to:
 (17)
(17)
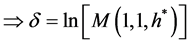 (18)
(18)
 (19)
(19)
The Equation (17) has apparently no closed form solution for  nevertheless, Gerber and Shiu [14] prove in their paper the existence and the uniqueness of the solution of our equation. The uniqueness of the parameter
nevertheless, Gerber and Shiu [14] prove in their paper the existence and the uniqueness of the solution of our equation. The uniqueness of the parameter  doesn’t mean in any way the uniqueness of the martingale measure, it infers only to the uniqueness of the Esscher transform martingale measure. The presence of the Gamma function impedes an analytic solution. Thus to solve Equation (16) we would need some numerical approaches.
doesn’t mean in any way the uniqueness of the martingale measure, it infers only to the uniqueness of the Esscher transform martingale measure. The presence of the Gamma function impedes an analytic solution. Thus to solve Equation (16) we would need some numerical approaches.
Having our martingale measure the price of a call option C on the Loss Index with a strike K at t = 0, can now be computed as follow:
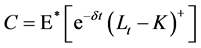 (20)
(20)
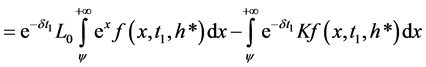 (21)
(21)
 (22)
(22)
Where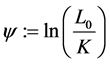 .
.
The Equation (22) resembles the Black & Scholes formula that is:  for some functions
for some functions .
.
For the special case where the scale parameter β is negligible i.e.  the Esscher MGF becomes:
the Esscher MGF becomes:
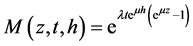 (23)
(23)
Thus 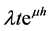 would be independent of
would be independent of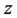 , hence the Esscher transformed function would have a Poisson distribution of parameter
, hence the Esscher transformed function would have a Poisson distribution of parameter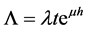 . In this case the Esscher transform CDF can be written as:
. In this case the Esscher transform CDF can be written as:
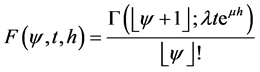 (24)
(24)
Where 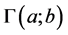 is the upper incomplete gamma function.
is the upper incomplete gamma function.
4. Correction of the Claim Amounts
In general, within the catastrophe insurance and especially for the earthquake insurance; it is very hard -if not impossibleto assess the exact amount of the claim caused by a catastrophe on the date of the occurrence. This amount is continually revised with time. The first amount is most of the time only an approximation of the real ultimate amount. In contrast with Schradin [15] who supposes that the re-estimation takes place only after the development period; we follow Jaimungal [4] et al. and Francesca Biagini et al. [16] supposing that the re-estimation befall right after the catastrophe.
Unlike these authors who build their model as a convolution of a semi-martingale process that has only one value per jump and the Claim size process; we want to model the re-estimation as a process that do not happen only once per catastrophe but we allow instead the claim to be re-corrected many times between two jumps.
Starting from this point the Loss index is not a pure jump process but rather a jump diffusion process. We then propose this model:
 (25)
(25)
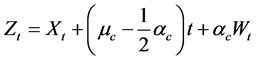 (26)
(26)
where 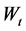 is a Wiener process.
is a Wiener process.  is the correction process (a geometric Brownian motion). This claim correction is done through time with a mean
is the correction process (a geometric Brownian motion). This claim correction is done through time with a mean  and a standard deviation of
and a standard deviation of . Note here that the correction happens continuously between the jumps(catastrophe occurrence) and not only once between two jumps.
. Note here that the correction happens continuously between the jumps(catastrophe occurrence) and not only once between two jumps.
4.1. Claim Correction and the Martingale Pricing
First let us compute the moment generating function of the process 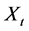 for
for .
.
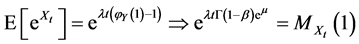 (27)
(27)
Note that 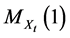 depends only on the value of t.
depends only on the value of t.
Proposition 1.
The process  is a
is a 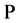 Martingale.
Martingale.
Proof: We obviously have to calculate the expectation of our process conditionally on 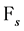 the filtration generated by the compound Poisson process up to time s. We have for
the filtration generated by the compound Poisson process up to time s. We have for :
:
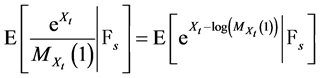 (28)
(28)
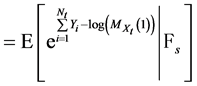 (29)
(29)
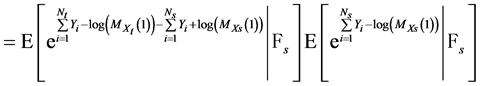 (30)
(30)

 (31)
(31)
The transition form (30) to (31) was done by adding and subtracting the same process from the equation then we could write the added process 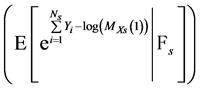 apart because it is
apart because it is 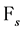 measurable. The other part is equal to:
measurable. The other part is equal to:
 (33)
(33)
 (32)
(32)
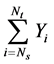 is the sum of the jumps with sizes
is the sum of the jumps with sizes 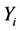 that occur between the time of the
that occur between the time of the  jump (i.e. at time s)
jump (i.e. at time s)
and the time of the manifestation of the  jump. Because the jumps are independent between the intervals and the only thing that matters is the length of our interval we have that
jump. Because the jumps are independent between the intervals and the only thing that matters is the length of our interval we have that 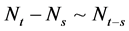 which induces that
which induces that
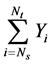 and
and 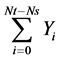 are equivalent. Then:
are equivalent. Then:
 (33)
(33)
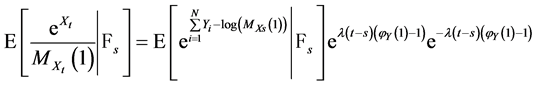 (34)
(34)
Finally, because  is
is 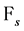 measurable we have:
measurable we have:
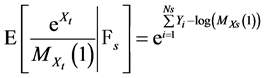 (35)
(35)
We deduce from Proposition 1 that the process 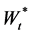 defined by the Equation (38) below:
defined by the Equation (38) below:
 (36)
(36)
is a Martingale.
It follows that the Radon-Nikodym derivative for our process  is written as:
is written as:
 (37)
(37)
where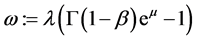 .
.
We are now in presence of 2 sources of randomness: the CPP and the Brownian motion which infers the non-completeness of the market. Therefore the measure martingale measure for a non-arbitrage pricing is not unique. The one that we presented here 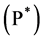 is just one of the existing martingale measures. Other martingales could eventually lead to different prices. As an example that we will propose hereafter a pricing using our new measure
is just one of the existing martingale measures. Other martingales could eventually lead to different prices. As an example that we will propose hereafter a pricing using our new measure 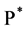 as well as a pricing with the Esscher transform.
as well as a pricing with the Esscher transform.
Theorem 1. The price of a call option on the Loss Index during the loss period if the risk neutral measure is  is given by:
is given by:
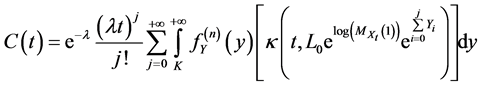 (38)
(38)
where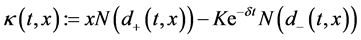 ;
; , and
, and  the n-fold convolution of the Gumbel PDF
the n-fold convolution of the Gumbel PDF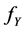 .
.
Proof: Recall that from Equation (26) in (25) the index’s dynamics equation is:

The index dynamics equation under the martingale measure 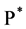 is represented by:
is represented by:
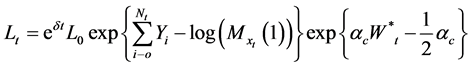 (39)
(39)
Thus:  (40)
(40)
Conditional on the σ-algebra:  the jump quantity
the jump quantity 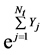 is known thus the quantity under the second expectation is just the price of an asset represented by a Geometric Brownian motion times a constant. Its value is then given by the Black & Scholes formula for an asset who’s valued
is known thus the quantity under the second expectation is just the price of an asset represented by a Geometric Brownian motion times a constant. Its value is then given by the Black & Scholes formula for an asset who’s valued  today. Conditioning on the jump size then on the number of jumps again gives the pricing in the Equation (38).
today. Conditioning on the jump size then on the number of jumps again gives the pricing in the Equation (38).
Concerning the jump component when the second expectation is performed, we used the  measure expectation as the intensity doesn’t change in the risk neutral world according to Merton [17] since the risk induced by the jumps is diversifiable. This price formula comes inaccordance with Jaimungal’s [4] pricing of a catastrophe option when the interest rate is stochastic.
measure expectation as the intensity doesn’t change in the risk neutral world according to Merton [17] since the risk induced by the jumps is diversifiable. This price formula comes inaccordance with Jaimungal’s [4] pricing of a catastrophe option when the interest rate is stochastic.
Using an Esscher transform approach should give a different pricing equation since -as we stated abovethe martingale measure is not unique.
4.2. The Esscher Pricing with Claim Correction
We will derive hereafter the price of a call on an index that includes a claim correction process.
To do so we proceed in the same way we dealt with the case without continues corrections. First we calculate our new MGF, then extract the new Esscher parameter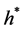 , apply it to the non-arbitrage condition then we end up with our price expression.
, apply it to the non-arbitrage condition then we end up with our price expression.
 (41)
(41)
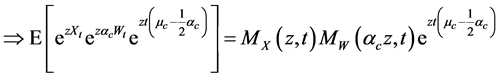 (42)
(42)
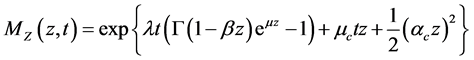 (43)
(43)
The Esscher MGF is then:

Then  can be found by solving the equation:
can be found by solving the equation:
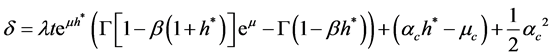 (44)
(44)
The option pricing formula will be the same as before with a different  and CPP CDF.
and CPP CDF.
 (45)
(45)
 is the CDF of a CPP with diffusion.
is the CDF of a CPP with diffusion.
As predicted this valuation might be different from the one given before. Now that all our pricing formulas are given for the loss period, our current task is to price the option in the development period.
5. Pricing in the Development Period
During the development period we assist only to the correction of the claims. The index on which our option is based, by convention, do not take into consideration the new jumps even if a catastrophe may happen during this period. Thus it turns out that the loss index becomes a pure geometric Brownian motion during the development interval. We can then, rewrite our loss index ass follow:
 (46)
(46)
Within the first model,  is:
is:
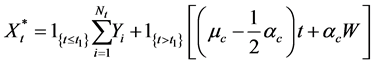 (47)
(47)
For the case accounting for claim correction 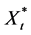 is:
is:
 (48)
(48)
Observe that in the development period case the Brownian motion is present with a probability equal to 1 a.s. The pricing of the option during this period leads the two models to the same results, since during this interval the two models are equal and are both represented by a geometric Brownian motion only. Also, during this interval the price is unique for the two models as the only source of randomness is the Brownian motion. Therefore the Esscher pricing would give the same result as the martingale approach that yields to the Black & Scholes formula. For this reason we will present only the Esscher pricing.
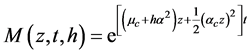 (49)
(49)
The transformed process is then normally distributed and our new  and call option price are:
and call option price are:
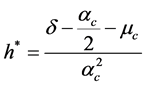 (50)
(50)
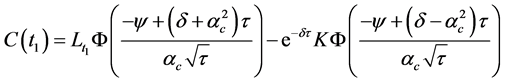 (51)
(51)
with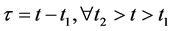 .
.
Now that all our pricing formulas are derived we need to build an algorithm to implement our pricing method in a way that would be practical for practitioners.
6. Numerical Example
We will show in this section how to use the previous results to calculate a call option on the Loss Index. As an example we will use only the case without claim correction as the later can be easily done by adding a Geometric Brownian motion to the basic model. Recall from the Equation (22) that the calculation of Call price needs the assessment of  then
then  the Esscher transformed function’s CDF.
the Esscher transformed function’s CDF.
The Esscher parameter is deducted from the Equation (19). Solving that equation can be done by the NewtonRaphson method. For our example we performed this using Matlab™ R2011b.
The next step is to assess  to do so we need to have the PDF of CPP with Gumbel sizes as the Equations (8) and (9) show. The CCP distribution is not available in programming languages, we thus have to assess it.
to do so we need to have the PDF of CPP with Gumbel sizes as the Equations (8) and (9) show. The CCP distribution is not available in programming languages, we thus have to assess it.
First, we generate a Gumbel distribution using the inverse method since this distribution do not exist in many programming languages.
If u is a random variable that follows a uniform distribution then the variable:
 (52)
(52)
has a Gumbel distribution with parameters  the location and scale parameters consecutively.
the location and scale parameters consecutively.
Once the size function created, N CPP random variables can be generated by following these steps:
1) generate a Poisson random variable  this variable represents the number of jumps;
this variable represents the number of jumps;
2) Simulate the Jump times by simulating S uniform random variables ;
;
3) Simulate S jump sizes  via Equation (52);
via Equation (52);
We get N CPP random variables via: .
.
Note that in practice this operation should be done only one time. Once a sufficient number of random variables are generated we can create a distribution table then get all our CDF values from it. This is possible because the catastrophe frequency is constant. Same thing can be said about the Gumbel distribution because in practice the claim average and dispersion (variance) are constant and rarely change. Only if a change in the data structure happens that an update is needed.
All we need now to get the price of our call option is to plug the CDF values in the Equation (22). Every time a new option with a new strike price is needed the same CPP table made before could be used we only need to be to replace the parameters in Equation (22). This fact is very important as the former proposed formulas (the martingale approach pricing) needs a large number of iterations whereas in our case the call price calculation is straightforward.
Clearly our price will differ according to these parameters. As the call option is a function of the CPP with Gumbel jump size, some analysis on the behavior of this distribution when the scale parameter β varies was performed.
A sample of 100,000 random variables was generated with the following parameterization: an interest rate δ = 2%, a location parameter μ = 1; we supposed that catastrophe occurs on average once every two years, the index’ current position is  unite8. The scale parameter’s range of values are
unite8. The scale parameter’s range of values are . The results are represented in the four following figures.
. The results are represented in the four following figures.
In Figure 1 the peak’s probability of occurrence lies between 0.06 and 0.08 for β = 1, then this probability is within  for
for  as it is shown through Figure 2. This probability shrinks to a value within
as it is shown through Figure 2. This probability shrinks to a value within 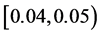 for
for  as we note from Figure 3 and drops to a value within
as we note from Figure 3 and drops to a value within 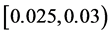 as it appears in Figure 4 for
as it appears in Figure 4 for . We conclude that the distribution gets flatter and the tails thinker with a higher values of the parameter
. We conclude that the distribution gets flatter and the tails thinker with a higher values of the parameter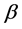 . So, the scale parameter acts on the CPP the same way it acts on the Gumbel distribution. The higher its value the flatter the Kurtosis.
. So, the scale parameter acts on the CPP the same way it acts on the Gumbel distribution. The higher its value the flatter the Kurtosis.
In a second time, we extracted the Esscher martingale parameter  for different scale parameter values. In this step, the location parameter μ is set to be equal to 11 and we let β vary from 2 unites to 10 unites with a step of 0.1 unites. We obtain a convex curve as shown in Figure 5.
for different scale parameter values. In this step, the location parameter μ is set to be equal to 11 and we let β vary from 2 unites to 10 unites with a step of 0.1 unites. We obtain a convex curve as shown in Figure 5.
For each value of β a CPP with Gumbel jumps are generated then the corresponding call price is assessed. The results are shown in Figure 5. The curve converges to 0 when β approaches μ’s value.
The corresponding call option prices are displayed in Figure 6. This price is increasing with the scale parameter until it reaches the value of 1 unite. The explanation of this phenomenon is simple. The strike value K
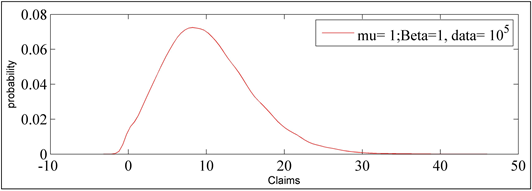
Figure 1. Compound Poisson process with β = 1 and μ = 1.
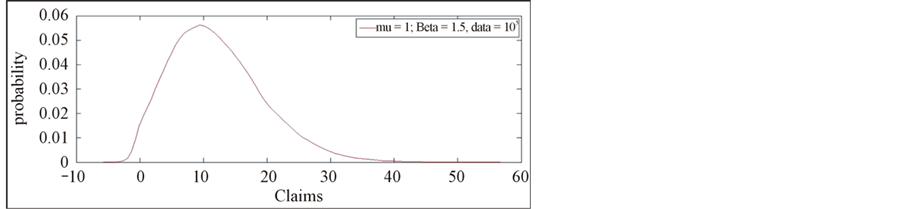
Figure 2. Compound Poisson process with β = 1.5 and μ = 1.
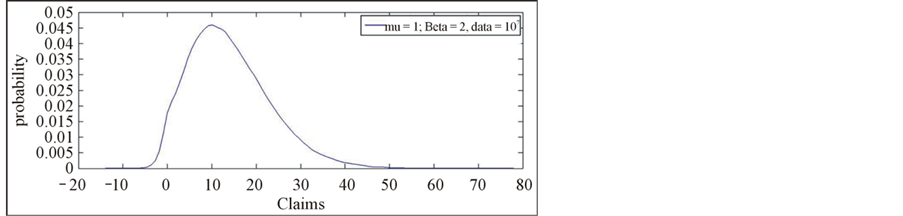
Figure 3. Compound Poisson process with β = 2 and μ = 1.
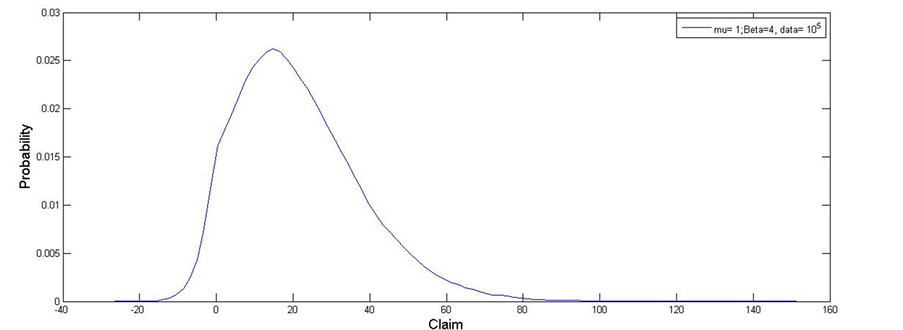
Figure 4. Compound Poisson process with β = 4 and μ = 1.
= 30 is located in the right tail of our CPP; and since higher β values makes the distribution flatter the tails become thicker and the probability of attaining K becomes greater, so will be the probability for the option to be in the money. This drives the call price to get more expensive. In reality the strike price might be also located far from the median as the insurance company seeks to hedge the extraordinary risk only.
The equations are an exception to the prescribed Note that in this article, we choose to not perform in the price of the option when we account for claim correction as is extracted simply by adding a Brownian motion to our CPP CDF in the pricing equation of our base

Figure 5. Esscher parameter value for different scale parameters.
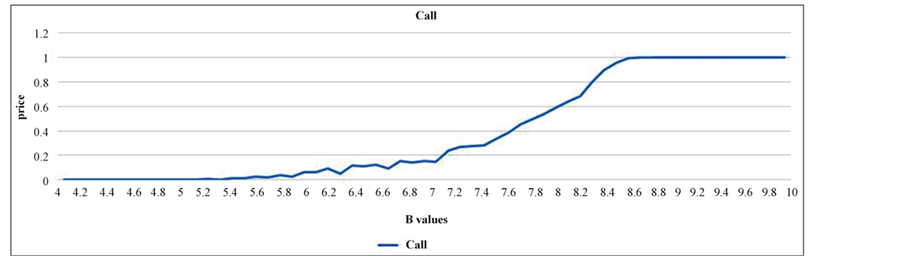
Figure 6. Call price for different scale parameter’s values.
model. Also it is worth noticing that the Esscher approach is faster and doesn’t need many iterations to be for its price computation as the martingale approach does as it appears in Equation (39). The development period pricing is also omitted because it yields to nothing new but the famous Black & Scholes price.
7. Conclusions
In this paper, we started by assessing the probability distribution of the jump sizes of the catastrophe claim amounts. For this purpose, the Extreme Value Theory happened to be a useful tool. Using the first definition of a sample’s maximum, we deducted that amounts of our extraordinary claims followed a Gumbel distribution. Using the Esscher transform, we extracted our martingale measure and then the expression of a call option on the Loss Index price. The resulted pricing is given in a closed form. Also, for its practical adaption, it doesn’t require complicated calculation to be assessed.
To confirm the underpinning theory of the model, we ran some numerical experiments showing how the call price can be calculated in practice. Since the catastrophe data are stable in time, the parameterization of the call price function also does not change, which makes the calculation of other options easier.
For further research, we suggest using the Peak over Threshold method to assess the jump sizes. This would eventually lead to a Generalized Pareto Law and more specifically a Pareto type distribution. The MGF is unfortunately not defined in all variable’s domain, and hence one needs to use other approaches to assess call prices.
REFERENCES
- H. Cox, J. Fairchild and H. Pederson, “Valuation of Structured Risk Management Products,” Insurance: Mathematics and Economics, Vol. 34, No. 2, 2004, pp. 259-272. http://dx.doi.org/10.1016/j.insmatheco.2003.12.006
- H. Geman and M. Yor, “Stochastic Time Change in CAT Option Pricing,” Insurance: Mathematics and Economics, Vol. 21, No. 2, 1997, pp. 185-193. http://dx.doi.org/10.1016/S0167-6687(97)00017-6
- A. Muerman, “Actuarially Consistent Valuation of CAT Derivatives,” Working Paper of the Wharton Financial Institution Center, 2003, 3-18.
- S. Jaimungal and T. Wang, “Catastrophe Options with Stochastic Interest Rates and Compound Poisson Losses,” Insurance: Mathematics and Economics, Vol. 38, No. 3, 2006, pp. 469-483. http://dx.doi.org/10.1016/j.insmatheco.2005.11.008
- A. Dasios and J.-W. Jang, “Pricing of Catastrophe Reinsurance and Derivatives Using the Cox Process with Shot Noise Intensity,” Finance and Stochastics, Vol. 7, No. 1, 2003, pp. 73-95. http://dx.doi.org/10.1007/s007800200079
- J. C. Duan and S. Giambastiani, “Faire Insurance Guaranty Premia in Presence of Risk Based Capital Regulations, Stochastic Interest Rate and Catastrophe Risk,” Journal of Banking and Finance, Vol. 28, No. 10, 2005, pp. 2435-2454. http://dx.doi.org/10.1016/j.jbankfin.2004.08.012
- T. Fujita, N. Ishimura and D. Tanaka, “An Arbitrage Approach to the Pricing of Catastrophe Options Involving the Cox Process,” Hitotsubashi Journal of Economics, Vol. 49, No. 2, 2008, pp. 67-74.
- H. Kanamori, “Earthquake Prediction: An Overview,” IASPEI Handbook of Earthquake and Engineering Seismology, 2000.
- S. Coles, “An Introduction to Statistical Modelling of Extreme Values,” Springer Series in Statistics, 2001. http://dx.doi.org/10.1007/978-1-4471-3675-0
- I. A. Fraga and C. Neves, “Extreme Value Distributions,” International Encyclopedia of Statistical Science, 2011. http://dx.doi.org/10.1007/978-3-642-04898-2_246
- M. Evans, N. Hastings and J. Peacock, “Statistical Distributions” 3rd Edition, Wiley, New York, 2000.
- N. L. Johnson, S. Kotz and A. W. Kemp, “Univariate Discrete Distributions”, 2nd Edition, John Wiley and Sons, New York, 1992.
- F. Esscher, “On the Probability Function in the Collective Theory of Risk,” Skandinavisk Aktuarietidskrift, Vol. 15, No. 3, 1932, pp. 175-195. http://dx.doi.org/10.1080/03461238.1932.10405883
- U. H. Gerber and E. S. W. Shiu, “Martingale Approach to Pricing Perpetual American Options,” ASTIN Bulletin, Vol. 24, No 2, 1994, pp. 1995-220. http://dx.doi.org/10.2143/AST.24.2.2005065
- H. R. Schradin, “PCS Catastrophe Insurance Options a New Instrument for Managing Catastrophe Risk,” Zeitschrift für die gesamte Versicherungswissenschaft, Vol. 83, 1994, pp. 633-682.
- F. Biagini, Y. Bergman and T. Meyer-Brandis, “Pricing of Catastrophe Insurance Options under Immediate Loss Reestimation,” Journal of Applied Probability, Vol. 45, No. 3, 2008, pp. 831-845. http://dx.doi.org/10.1239/jap/1222441832
- R. C. Merton, “Option Prices When Underlying Stock Returns Are Discontinuous,” Journal of Financial Economics, Vol. 3, No. 1-2, 1976, pp. 125-144. http://dx.doi.org/10.1016/0304-405X(76)90022-2
NOTES

1see H. R. Schradin, PCS Catastrophe Insurance OPTIONS-A New Instrument for Managing Catastrophe Risk, AFIR/ERM colloquium, Nurenberg Germany, october1996 and http://www.verisk.com/property-claim-services/pcs-catastrophe-serial-numbers.html.

2There exist some models in seismology and methodology for earthquake prediction but no one is known to be efficient. Clearly, the existence of previous disasters was known at their happening time or few hours before.
3As some researches in seismology confirm the independent characteristic of the earthquakes. For more details see .
4For more details see: Stuart Coles and Antony Davison .

5We present hereafter the non-normalized version of the Gumbel as it represent the general case.

6See Evans, Hastings and Peacock (2000) , “Statistical Distributions”, 3rd. Ed., John Wiley and Sons, Chapter 15 and Johnson, Kotz, and Kemp, (1992) , “Univariate Discrete Distributions”, 2nd. Ed., John Wiley and Sons Chapter 22 for the Maximum likelihood equation for the estimation of μ and β.
7See .

8To simplify our matters we used here units .1 unite could represent $ 106.

