Journal of Mathematical Finance
Vol.3 No.3A(2013), Article ID:37587,6 pages DOI:10.4236/jmf.2013.33A003
The Hidden Risk Factor
Record Currency Management, Windsor, UK
Email: jwitte@recordcm.com, dples@recordcm.com, jcorominas@recordcm.com
Copyright © 2013 J. H. Witte et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 19, 2013; revised August 21, 2013; accepted September 10, 2013
Keywords: Currency Risk; Risk Premium; Risk Factor; FX Hedge; Currency Overlay
ABSTRACT
To achieve maximum returns consistent with an investor’s appetite for risk, the correct identification and estimation of all relevant risk factors in a portfolio are necessary. In this paper, we identify the role of foreign currency as an important risk factor from an international investor’s point of view.
1. Introduction
It has been noted repeatedly (cf. [1]) that, since the start of the financial crisis in 2007, global asset correlation has been increased steadily. This effect has made it much harder for portfolio managers to achieve performance alpha by skillfully selecting superior investment opportunities. In order to outperform in such a world (cf. [2]), investors have to correctly identify and characterise the available risk premia, and build a portfolio that matches their appetite for risk while attempting maximum diversification (cf. [3,4]).
A risk factor is usually understood to be any variable that contributes to explaining the composition of the total portfolio risk. This means that if we can decompose the total portfolio risk into different components, i.e., the different risk factors, then this will give us a clearer understanding of where our existing risk originates. More importantly, it allows us to analyse the risk premia of the different risk factors, and enables us to make sure that these are consistent with our overall requirements for diversification and appetite for risk.
In a sense, a risk factor analysis reverses the view taken by Markowitz’s modern portfolio theory (cf. [5,6]). In a Markowitz setting, an investor makes his investment decisions ex ante, based on his expectations about the statistical properties of the individual assets under consideration. In contrast, in a risk factor analysis, we look at the portfolio ex post, attempting to describe the total portfolio risk as accurately as possible by decomposing it into the different drivers of risk, the main risk factors. This enables us to observe effects that show a big impact only if considered in aggregate in a large portfolio.
In this paper, we show that currency is an important risk factor to an international investor, and we emphasise that any change in an investor’s international currency position may increase or decrease the total portfolio risk, depending on market circumstances. Therefore, the reward/risk ratio induced by currency, in line with classic risk factors such as equities, inflation, and credit, has to be regarded as indicative for investment performance. In particular, we attempt to quantify the extent to which such change would impact portfolio risk.
The effect of currency on international investments has been widely studied in the literature. In [7], it is discussed how country factors affect stock prices far more than, e.g., market sectors and industries, and most of this difference can be attributed to currency (see also [8]). In [9], the currency risk premium is compared to market risk premium, and the interaction between the two is analysed; in some ways, this is a first step towards the more recent studies on the marginal contribution of specific risk factors.
Over the past decade, we have also seen an expansion in the literature on risk factors and the calculation of marginal risk contributions to portfolio risk, as investors have become increasingly concerned with downside management (see for example [1,2,10-12]) and have recognised the need for an improved understanding of the impact of risk factors.
This paper is structured as follows. In Section 2, we introduce our definitions of risk and a risk factor. In Section 3, we introduce our approach to risk factor analysis. In particular, we introduce the notion of risk factor decomposition and risk factor impact. In Section 4, we discuss in detail how an elevated risk factor is to be interpreted in our framework. In Section 5, we apply our methodology to a representative international portfolio, and we compare the risk factor impacts of the most commonly studied risk factors. We demonstrate that, empirically, currency is an important risk factor to an international investor. We conclude by summarising our findings in Section 6.
2. Defining a Risk Factor
Consider a portfolio of return sources, and consider an investor who is holding this portfolio with the aim of maintaining or increasing its value over some future time horizon. In this setting, we define risk as follows.
Definition 1. Risk is the (exposure to) the possibility of unpredicted portfolio moves; every chance or situation involving such a possibility.1 Hence, risk is defined based on unexpected changes to our portfolio value. We then move on to very generally defining a risk factor as anything providing us with information about our portfolio risk.
Definition 2. A risk factor is a variable associated with the magnitude of portfolio risk.2
We emphasise the following corollary, which is at times overlooked.
Corollary 1. Risk factors are correlational, not necessarily causal. Correlation does not imply causation.
For example, a fund manager who is fully invested in shares of a single company will not necessarily underperform in a group of more diversified managers. He is merely more likely to underperform due to higher volatility, but his lack of diversification does not imply underperformance (e.g., imagine he had bought shares in Apple or Google early on).
3. The Risk Factor Challenge
In the previous section, we have very generally introduced the notion of risk and risk factor. We will now explain how portfolio risk can be analysed by studying a portfolio’s risk factors.
3.1. Risk Factor Decomposition
We start by introducing what we understand to be a risk factor decomposition of a given portfolio.
Definition 3. Suppose our portfolio return is described by the random variable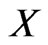 . A risk factor decomposition is any finite number of random variables
. A risk factor decomposition is any finite number of random variables 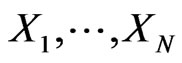 and scalar values
and scalar values 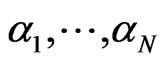 such that
such that
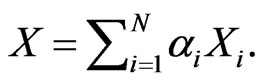 (1)
(1)
In this case, the portfolio variance is given by
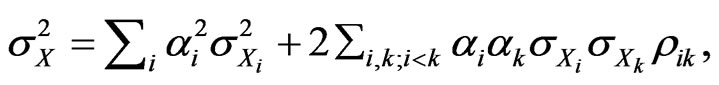
where 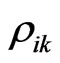 is the correlation coefficient of
is the correlation coefficient of 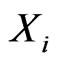 and
and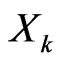 , and
, and 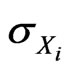 is the standard deviation of
is the standard deviation of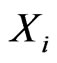 . We denote the portfolio risk by
. We denote the portfolio risk by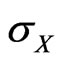 .
.
Remark 1. One way of constructing a risk factor decomposition as given in Equation (1) is to consider 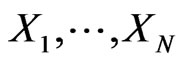 as the returns of the individual assets in our portfolio, with
as the returns of the individual assets in our portfolio, with 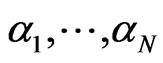 denoting the respective weights of the exposure. However, this is by no means a unique decomposition of
denoting the respective weights of the exposure. However, this is by no means a unique decomposition of .
.
In Section 5, we will explain how to also analyse other risk factors, such as inflation and credit. Any decomposition into return sources can form a foundation for a risk factor analysis.
Remark 2. By Equation (1), a risk factor decomposition does not allow for any purely correlational risk factors, as these do not add to the information contained in the causational factors. Put differently, this means that a risk factor which has no impact on portfolio volatility will not be admitted in the decomposition.
3.2. Risk Factor Impact
To measure the particular effects of the different risk factors on our total portfolio risk, we come to define what we understand to be the risk factor impact.
We aim to measure risk impact of a factor 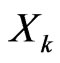 by taking into account the following three aspects.
by taking into account the following three aspects.
1) Weight : exposure to
: exposure to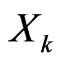 .
.
2) Volatility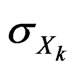 : volatility of
: volatility of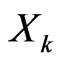 .
.
3) Correlation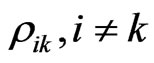 : relationship to the other factors
: relationship to the other factors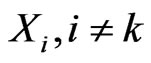 .
.
In detail: we want the risk factor impact to increase/ decrease in accordance with weight or volatility; and we want the risk factor impact to increase and decrease, respectively, with positive and negative cumulative correlation to the other risk factors. Our mathematical definition is as follows.
Definition 4: Consider the risk factor decomposition (1). We define the impact of risk factor 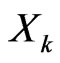 to be
to be
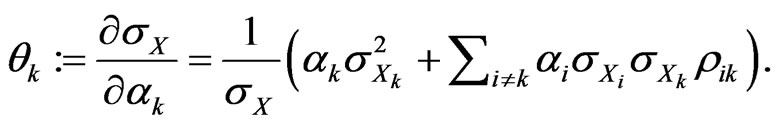 (2)
(2)
From Equation (2), we see how  generally respects the desired characteristics listed in 1), 2), and 3).
generally respects the desired characteristics listed in 1), 2), and 3).
More specifically, since  is the partial derivative of
is the partial derivative of 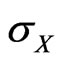 by
by , it measures the rate of change of the portfolio volatility
, it measures the rate of change of the portfolio volatility 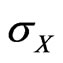 in response to small changes in the weight
in response to small changes in the weight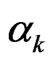 . In other words, it is the marginal risk contribution of factor
. In other words, it is the marginal risk contribution of factor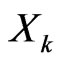 . We will clarify this property in Section 4.
. We will clarify this property in Section 4.
3.3. A Two Asset Portfolio
Consider a portfolio return 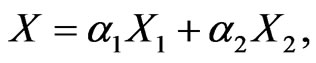 consisting of the returns
consisting of the returns 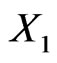 and
and 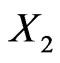 of two assets, with weights
of two assets, with weights  and
and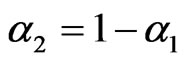 , respectively. The portfolio variance is given by
, respectively. The portfolio variance is given by
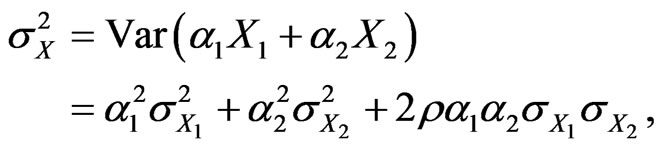
where  denotes the correlation coefficient of
denotes the correlation coefficient of  and
and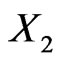 , and we have
, and we have
 (3)
(3)
for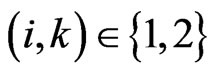 ,
,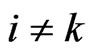 .
.
Example 1. Suppose 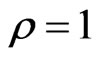 and
and . We have
. We have 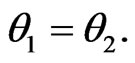
Hence, for equally volatile and perfectly correlated risk factors, the risk factor impacts are identical.
Suppose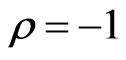 . In this case, we have
. In this case, we have
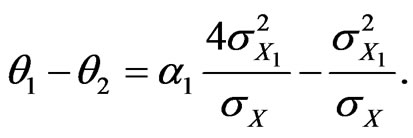
Hence, in a portfolio with two perfectly anticorrelated assets, the difference between the risk factor impacts scales linearly with the weight .
.
Suppose . In this case, Equation (3) becomes
. In this case, Equation (3) becomes
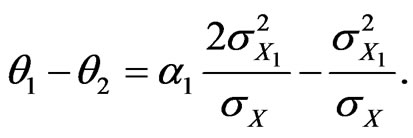 (4)
(4)
In a portfolio with two perfectly independent assets that are equally volatile, the allocation  between the two assets linearly determines which of the two has the higher impact.
between the two assets linearly determines which of the two has the higher impact.
Suppose 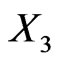 is a third asset with weight
is a third asset with weight 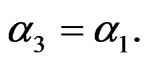 Suppose
Suppose 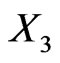 is independent of
is independent of  and
and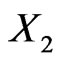 . Suppose that
. Suppose that 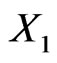 and
and 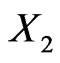 are correlated by
are correlated by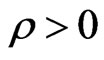 , and that
, and that 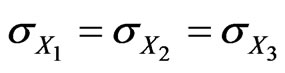 . In this case, we have
. In this case, we have

We observe that, because 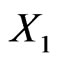 is correlated with
is correlated with , the risk factor impact of
, the risk factor impact of  is greater than that of
is greater than that of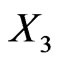 .
.
In other words, if we add a third asset to our portfolio which is strongly correlated with one of the two we already have, then the third asset will have a higher risk impact than if it was slightly correlated or independent.
Example 2. Suppose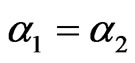 . We have
. We have
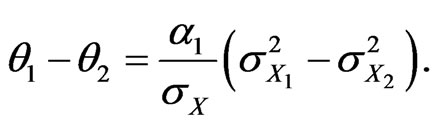 (5)
(5)
Hence, for two equally weighted assets, the difference between the risk factor impacts scales linearly with the difference in variance, independently of the correlation coefficient.
Suppose, in addition, that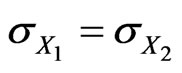 . We have
. We have

Hence, for two equally volatile assets with equal weights, the risk factor impacts are identical, independently of the correlation coefficient. This is desireable since, all else being equal, the correlation coefficient contains no information that can be used to measure the relative impacts of the individual risk factors.
4. What a High Risk Factor Impact Means
Suppose our portfolio return is described by the random variable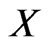 . Suppose we have a risk factor decomposition
. Suppose we have a risk factor decomposition

Remark 3. Consider two risk factors 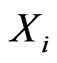 and
and 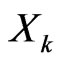 with impacts
with impacts 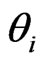 and
and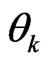 , respectively. Suppose
, respectively. Suppose . In this case, adding a small quantity to the weight of
. In this case, adding a small quantity to the weight of 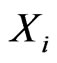 will add more risk to our portfolio than increasing the weight of
will add more risk to our portfolio than increasing the weight of 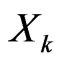 by the same quantity. The opposite effect holds when decreasing the weight by small quantities.
by the same quantity. The opposite effect holds when decreasing the weight by small quantities.
We present this property more rigorously in the following theorem.
Theorem 1. Consider two risk factors 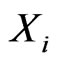 and
and 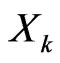 with impacts
with impacts  and
and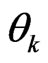 , respectively. Suppose
, respectively. Suppose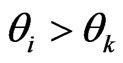 . Then, there exists a threshold
. Then, there exists a threshold  such hat
such hat
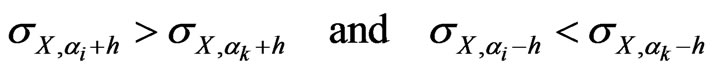 (6)
(6)
for all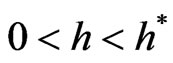 , where
, where  denotes the standard deviation of
denotes the standard deviation of
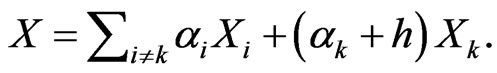
Proof. Suppose 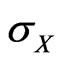 is differentiable with respect to
is differentiable with respect to  and
and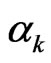 , respectively. We have
, respectively. We have

Let 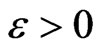 such that
such that . There exists
. There exists 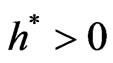 such that
such that
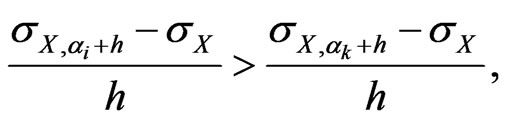
for all  and
and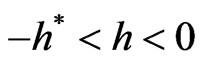 , which is equivalent to Equation (6), which proves the theorem. ■
, which is equivalent to Equation (6), which proves the theorem. ■
5. Analysis of an International Portfolio
We now come to apply the risk factor methodology introduced in this paper to an actual investment scenario. We study two sample portfolios as outlined below; in Tables 1 and 2, we indicate return sources, data sources, and weights.
For each of the two sample portfolios, we derive a risk factor decomposition and compute the marginal risk contributions of a series of pre-defined risk factors. We proceed as follows.
We analyse the following risk factors; our choice is driven by the risk premia we believe investors are seeking to exploit3.
• International Equity
• Currency
• Cash
• Domestic Equity
• Inflation (Duration + Term Premium)
• Credit
• Commodities
Certain risk factors are not directly investible in the sense that they depend on two or more carrier assets to be identified. This is the case with inflation, credit, and currency. Still, they are important risk factors when making forward looking judgements about markets within a Global Tactical Asset Allocation (GTAA) framework, for instance. We capture these by rewriting the equations as Currency = Int. Equities − Hedged Int. Equities Inflation = Government Bonds − Cash Credit = Corporate Bonds − Government Bonds This decomposition helps bring to light certain risk factors which would otherwise not be directly observable and quantifiable in an appropriate manner since they are embedded in other asset classes, yet can represent a substantial risk to the portfolio. Currency is our main example here.
Based on the monthly returns of the listed indices, we compute a rolling standard deviation and correlation for all factors, using a 12 months look back window. In other words, for every month, we estimate 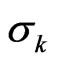 and
and 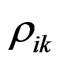 from the previous 12 data points,
from the previous 12 data points, 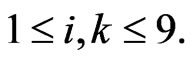 Together with the weights
Together with the weights ,
, 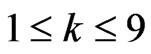 , indicated in Tables 1 and 2, we then have all required information to calculate the risk factor impacts
, indicated in Tables 1 and 2, we then have all required information to calculate the risk factor impacts ,
, 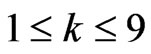 , on a monthly basis, following Equation (2).
, on a monthly basis, following Equation (2).
Our monthly data set starts in January 1994 and ends in June 2012. We rebalance our sample portfolio monthly to maintain the constant weights given in Tables 1 and 2.
How to interpret each risk factor? To make the decomposition intelligible in a single framework, Figures 1 and 2 illustrate the size of each risk factor relative to the total size of all risk factors: it shows the absolute marginal risk contribution of each risk factor relative to the aggregate measure of such absolute marginal risk contributions (see also Table 3).
In mathematical terms, Figures 1 and 2 show our monthly values for
 (7)
(7)
describing the evolution of the relative absolute magnitude of all risk factor impacts over time.
Remark 4. Unlike the notion of risk factor impact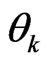 , introduced in Section 3.2, the absolute values
, introduced in Section 3.2, the absolute values  shown in Figures 1 and 2 do not contain any directional
shown in Figures 1 and 2 do not contain any directional
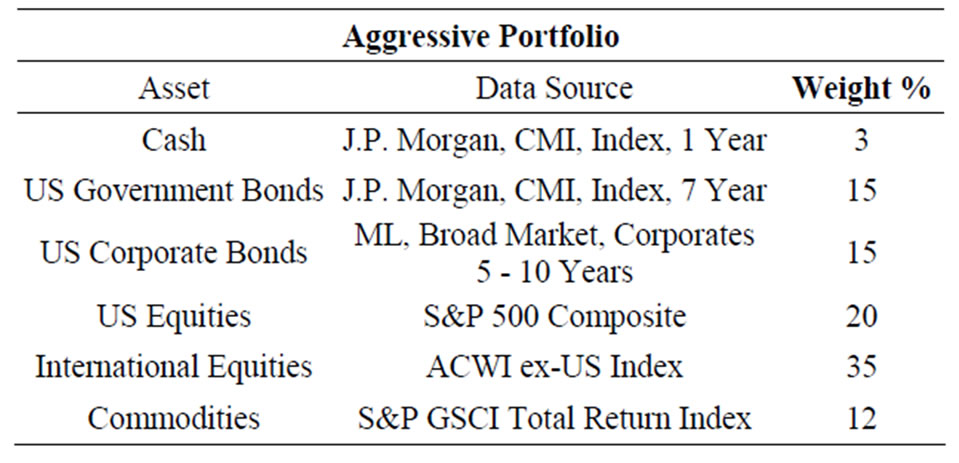
Table 1. Allocation and data source. Aggressive sample portfolio.
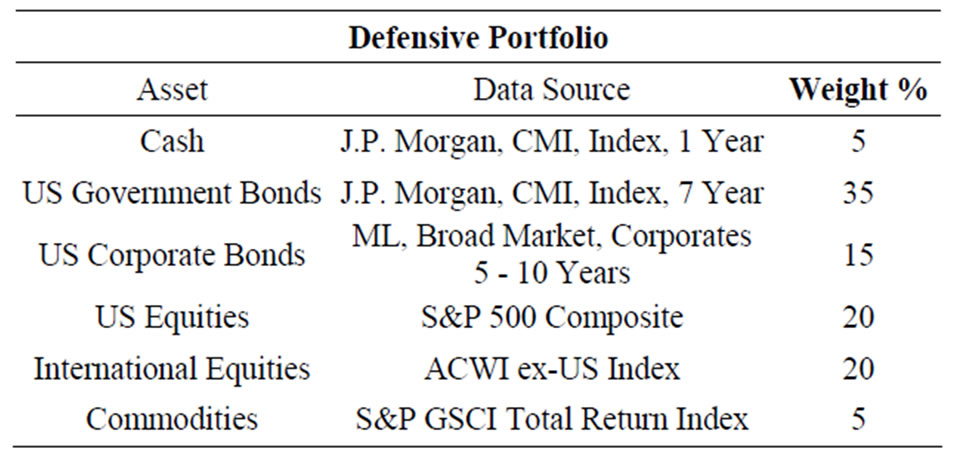
Table 2. Allocation and data source. Defensive sample portfolio.

Table 3. Based on monthly returns, we compute a rolling standard deviation and correlation for all factors, using a 12 months look back window. We then compute the risk factor impacts on a monthly basis. In the table below, we see the June 2012 values for the defensive sample portholio.
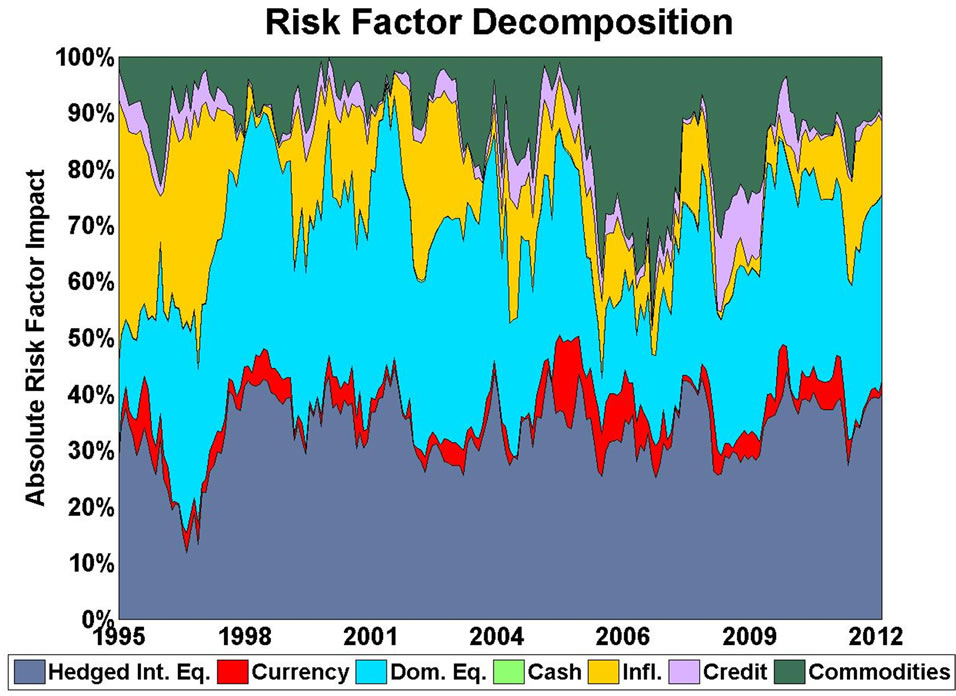
Figure 1. Risk factor impacts. Aggressive sample portfolio.
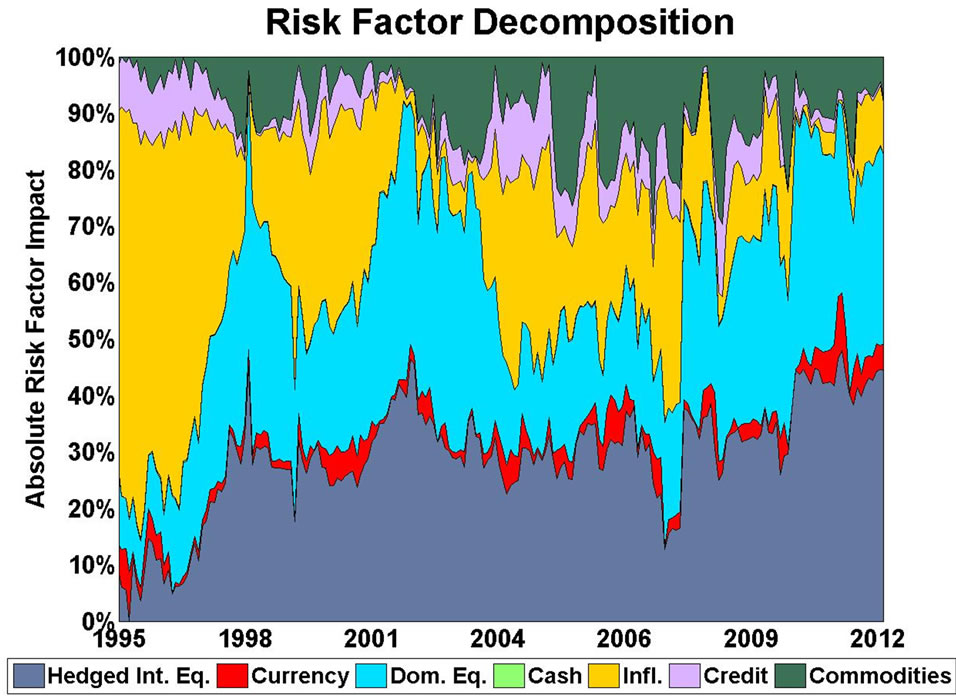
Figure 2. Risk factor impacts. Defensive sample portfolio.
information.
The absolute values in Equation (7) indicate the magnitude to which changes in the exposure to different risk factors affect the total volatility of investment performance. It serves as an index of risk relevance.
The directionality says whether an increased exposure to a risk factor results in an increased or decreased overall volatility. It can only be meaningfully evaluated when studying the risk factor impact in conjunction with the expected returns of the different factors. In that case, the risk factor impacts can serve as a starting point for recalibration of portfolio weights.
6. Conclusions
In this paper, we have introduced a theoretical framework for risk factor analysis. We have introduced the risk factor impact as
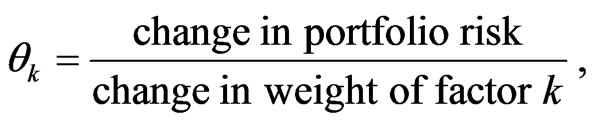
which presents a unique way of understanding the effects of risk factor weights on the total portfolio risk. Our measure of risk factor impact is identical to the marginal risk contribution, and we provide a rigorous account why this measure is of relevance and how to interpret it.
By studying a representative global portfolio, we have empirically analysed the different risk factor impacts with particular focus on currency. We find that an international investor’s currency exposure is one of the most impactful risk factors. This suggests that currency exposure, in line with classic risk factors as domestic and international equities, inflation, credit, and commodities, is indicative of future investment performance. Hence, currency exposure, together with all assets in a portfolio, should be given thoughtful and prudent risk and return analysis to help guide an investor’s expectations.
REFERENCES
- S. Page and M. Taborsky, “The Myth of Diversification: Risk Factors versus Asset Classes,” Journal of Portfolio Management, Vol. 37, No. 4, 2011, pp. 1-2. http://dx.doi.org/10.3905/jpm.2011.37.4.001
- D. Rosen and D. Saunders, “Risk Factor Contributions in Portfolio Credit Risk Models,” Journal of Banking and Finance, Vol. 34, No. 2, 2010, pp. 336-349. http://dx.doi.org/10.1016/j.jbankfin.2009.08.002
- J. Lintner, “The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets,” The Review of Economics and Statistics, Vol. 47, No. 1, 1965, pp. 13-39. http://dx.doi.org/10.2307/1924119
- O. Ruban and D. Melas, “Risk Parity Portfolios: Rebalance, Leverage, Or Both?” The Journal of Investing, Vol. 20, No. 1, 2011, pp. 99-108. http://dx.doi.org/10.3905/joi.2011.20.1.099
- H. M. Markowitz, “Portfolio Selection,” The Journal of Finance, Vol. 7, No. 1, 1952, pp. 77-91.
- H. M. Markowitz, “Portfolio Selection: Efficient Diversification of Investments,” John Wiley & Sons, New York, 1958.
- J. Diermeier and B. Solnik, “Global Pricing of Equity,” Financial Analysts Journal, Vol. 57, No. 4, 2001, pp. 37- 47. http://dx.doi.org/10.2469/faj.v57.n4.2464
- J.-F. L’Her, O. Sy and M. Y. Tnan, “Country, Industry, and Risk Factor Loadings in Portfolio Management,” The Journal of Portfolio Management, Vol. 28, No. 4, 2002, pp. 70-79. http://dx.doi.org/10.3905/jpm.2002.319856
- G. De Santis and B. Gerard, “How Big Is the Premium for Currency Risk?” Journal of Financial Economics, Vol. 49, No. 3, 1998, pp. 375-412. http://dx.doi.org/10.1016/S0304-405X(98)00029-4
- A. S. Cherny and D. B. Madan, “Coherent Measurement of Factor Risks,” 2006. http://arxiv.org/abs/math/0605062v1
- J. Bender, R. Briand, F. Nielsen and D. Stefek, “Portfolio of Risk Premia: A New Approach to Diversification,” The Journal of Portfolio Management, Vol. 36, No. 2, 2010, pp. 17-25. http://dx.doi.org/10.3905/JPM.2010.36.2.017
- S. Maillard, T. Roncalli and J. Teiletche, “On the Properties of Equally-Weighted Risk Contributions Portfolios,” The Journal of Portfolio Management, Vol. 36, No. 4, 2010, pp. 60-70. http://dx.doi.org/10.3905/jpm.2010.36.4.060
- MSCI Barra, “Barra Risk Model Handbook,” 2007.
- C. R. Harvey, “The Risk Exposure of Emerging Equity Markets,” The World Bank Economic Review, Vol. 9, No. 1, 1993, pp. 19-50. http://dx.doi.org/10.1093/wber/9.1.19
NOTES
1See also [13].
2See also [14].
3It is important to note that there is no single unique risk factor decomposition for any given portfolio. That is, risk factors can be defined and analysed depending on what is intended to be shown.

