Journal of Mathematical Finance
Vol.3 No.4(2013), Article ID:38143,10 pages DOI:10.4236/jmf.2013.34043
An Extension of Some Results Due to Cox and Leland
Monash University, Clayton, Australia
Email: andrew.leung@monash.edu, apleung@gmail.com, wen.shi@monash.edu
Copyright © 2013 Andrew P. Leung, Wen Shi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 10, 2013; revised July 21, 2013; accepted August 9, 2013
Keywords: Path independence; Dynamic asset allocation; Dynamic optimization; Calculus of variations
ABSTRACT
We investigate an optimal portfolio allocation problem between a risky and a risk-free asset, as in [1]. They obtained explicit conditions for path-independence and optimality of allocation strategies when the price of the risky asset follows a geometric Brownian motion with constant asset characteristics. This paper analyzes and extends their results for dynamic investment strategies by allowing for non-constant returns and volatility. We adopt a continuous-time approach and appeal to well established results in stochastic calculus for doing so.
1. Introduction
Beginning with [2], diffusion processes have been the standard for modeling asset returns, despite empirical evidence that returns are not normally distributed. Dynamic asset allocations based on these processes have been prominent, for example see [3,4] and [5,6] provide a survey of this topic to the early 1990s.
Based on the work of [7] and [1,2] derived criteria for controls to optimize an investor’s objectives. They restricted the case to a portfolio with only two assets, a risky one paying no dividends and a risk-free one with the price of the risky asset following a geometric Brownian motion process.
The restriction to a single risky asset involves no significant loss of generality since the setting can be taken as a mutual fund. [8] shows that if geometric Brownian motion models are adopted, the separation theorem of mutual funds can be applied: in a portfolio problem of allocating wealth across many risky assets, the problem can be reduced to that of choosing amongst combinations of a few funds formed from these assets.
However, [1] assume constancy of asset characteristics, which is restrictive. In addition, their use of the discretetime binomial model, converging in continuous-time by limiting the time intervals, is cumbersome and detracts from the economics of the issue. Nonetheless, their result of efficiency of path-independent strategies has been extensively cited in the literature, especially in the studies for hedge funds.
[6] claim that, although the results presented by [1] were not well known at that time, path-independence of a strategy is often necessary for such a dynamic strategy to be optimal. In their study of hedge fund performance, when constructing a payoff function [9] stipulate that payoff must be a path-independent non-decreasing function of the index value, derived from [1].
[10] extend the relevance of path-independence to the case when prices of risky assets follow an exponential Lévy process. On the other hand, path-independent strategies are not always attractive. [11] show that pathdependent strategies are suboptimal for risk-averse investors when the pricing model is a function of the risky asset price at terminal time. However, and not surprisingly, path-dependent strategies are preferred if the pricing model of the risky assets is itself pathdependent.
In this paper, we extend the results of [1] for more general asset return processes. We assume that the price of the riskless asset grows deterministically at a variable interest rate, and the price for the risky asset follows geometric Brownian motion, with both the drift and volatility being variable over both time and the stock price. Such a model mitigates some of the difficulties in explaining long-observed features of the implied volatility surface for option pricing. Hence it is possible to model derivatives more realistically.
Detailed references for such stochastic processes may be found in [12,13]. Without loss of generality, we consider a world with a risky asset and a riskless asset, as in [1]. We establish our results by application of a continuous-time approach and the use of partial differential equations (PDEs), rather than through stochastic calculus. We obtain explicit results for general dynamic strategies which allow for uncertainty as modeled in diffusion processes. These results extend those of [1].
Our results are concerned with maximizing some form of investor utility. In most former studies, when dealing with utility maximization, a particular form of utility function is specified. For example, a HARA utility is considered in [2]; an iso-elastic utility in [14]; and a CRRA power utility in [15]. While the Hamilton-JacobiBellman equation is a popular tool for utility maximization problems, [16] criticizes the use of an arbitrary “bequest function” as the boundary condition in [2]; the boundary behavior around zero terminal wealth may be inconsistent with his “bequest function”. In our approach, the boundary condition is taken as an arbitrary utility function of terminal wealth, thereby avoiding this problem. [17] gives a more detailed review of expected utility maximization for strategies involving a risky and a riskless asset. Although he does not approach this problem in full generality, using the example of a power utility function, he shows how other cases can be solved with little effort.
In the working papers by [18,19], for a given utility function, the Feynman-Kac formula is used to find controls satisfying certain PDEs for utility maximization. We show that the Feynman-Kac formula can generally provide the solution to a control in terms of its terminal value. We also show that the terminal value satisfies some concave utility, without specifying its functional form.
The paper is organized as follows. First, for simplicity, we assume no cash flows, which corresponds to the pure “bequest” case of [7]. This assumption is then later relaxed.
• Section 2 extends Proposition 1 of [1] for necessary and sufficient conditions for an investment strategy to be feasible, where the controls of the strategy are given as functions of time and the value of the risky asset.
• Section 3 develops necessary and sufficient conditions for an investment strategy to be path-independent, with controls defined as functions of time and the value of the portfolio (wealth). These results extend Proposition 2 of [1].
• Section 4 establishes necessary and sufficient conditions for an investment strategy to optimize a concave utility, while imposing no constraints on portfolio allocations. This extends Proposition 3 of [1].
• Sections 5 and 6 consider the case of non-negative allocations.
• Section 7 considers the situation when cash with drawals are admissible.
• Section 8 concludes.
2. Controls Based on Stock Price 
Suppose  is total wealth, invested in a risky asset
is total wealth, invested in a risky asset  and a riskless asset
and a riskless asset  Suppose also that
Suppose also that
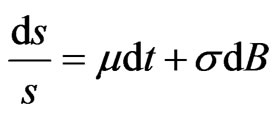 (1)
(1)
is the process for the risky asset, where  is Brownian motion1, and both
is Brownian motion1, and both 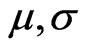 may depend on both
may depend on both  and
and 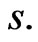 Itô’s theorem provides that:
Itô’s theorem provides that:
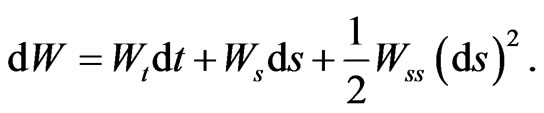
Let 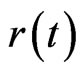 denote the riskless rate at time
denote the riskless rate at time 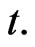 This is generally independent of the stock price
This is generally independent of the stock price  by virtue of being riskless.
by virtue of being riskless.
Then, when there are no cash withdrawals or injections (i.e. the strategy is self-financing),
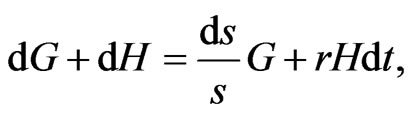
so that
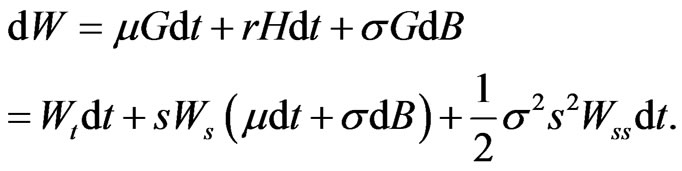 (2)
(2)
This implies that
 (3)
(3)
and
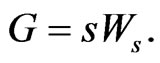 (4)
(4)
thus

and so
 (5)
(5)
These equalities are consistent with the conditions of Proposition 1 of [1]. Note that the expected return on the risky asset  does not appear in 5.
does not appear in 5.
Differentiating equation (5) with respect to  yields:
yields:
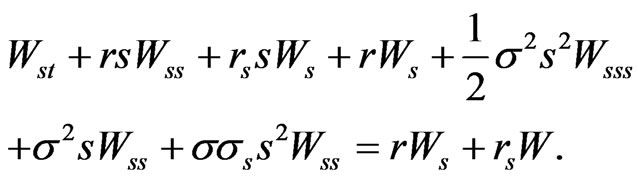
Multiplying this last equality by , we get
, we get

On the other hand since 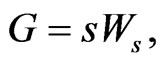 we have
we have

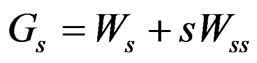
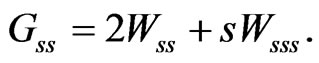
Hence:
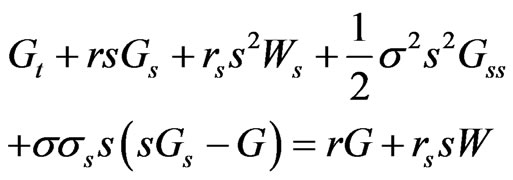
and, as 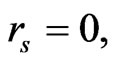 this may be formalized as:
this may be formalized as:
Proposition 1: The controls  and
and  satisfy the PDEs:
satisfy the PDEs:
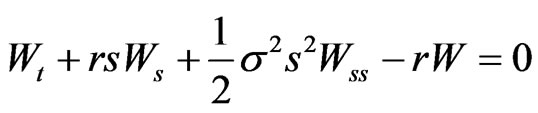 (6)
(6)
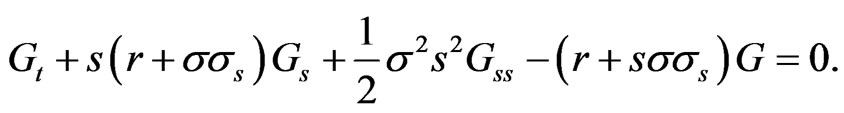 (7)
(7)
Remark: Thus proposition 1 of [1] will not apply for  if
if  However note that
However note that  has the same form as
has the same form as 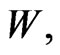 but with
but with  replaced by
replaced by 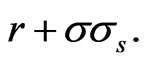
3. Controls Based on Wealth 
Since  we now consider
we now consider  and
and  as functions of
as functions of 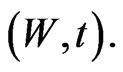 This corresponds to Proposition 2 of [1].
This corresponds to Proposition 2 of [1].
On this basis



Hence the left hand side of Equation (7) becomes

For the right hand side of equation (7):
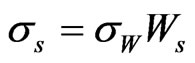
and so
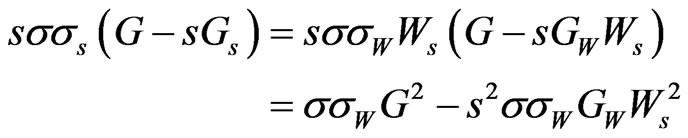
Hence we have:
Proposition 2: The control  viewed as a function of wealth, satisfies:
viewed as a function of wealth, satisfies:

Remark: This is the same as proposition 2 of [1] when 
4. Controls That Are Compatible with a Concave Utility
Consider a control 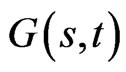 that maximizes an expected utility of terminal wealth
that maximizes an expected utility of terminal wealth  at time
at time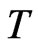 :
:

for some utility function 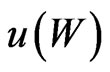 and where
and where 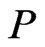 is the physical measure under the process in 1.
is the physical measure under the process in 1.
Then the equation (5) is, regarded as a parabolic partial differential equation:

where 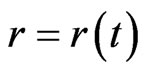 is a function of
is a function of  and
and  and
and  are functions of
are functions of .
.
The solution is given by the Feynman-Kac formula. The solution, expressed as a stochastic expectation, is:
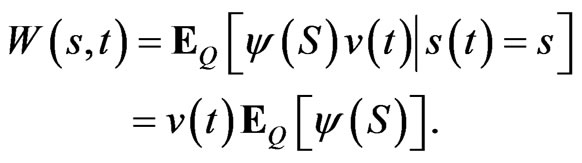 (9)
(9)
Here 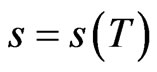 and
and 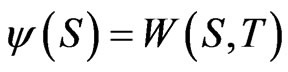 for a given value of
for a given value of 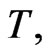 and
and

The expectation 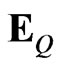 is taken with respect to the risk neutral process:
is taken with respect to the risk neutral process:
 (10)
(10)
Remark: It is known there are various conditions for the Feynman-Kac formula to hold, which are set out in the Appendix. A condition that 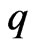 be bounded above zero is not onerous, as we are dealing with a risky asset. Some of these conditions may be relaxed significantly, and will be discussed in a further paper.
be bounded above zero is not onerous, as we are dealing with a risky asset. Some of these conditions may be relaxed significantly, and will be discussed in a further paper.
The probability density 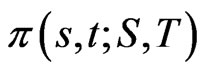 of
of  at time
at time  is governed by the Kolmogorov backward equation
is governed by the Kolmogorov backward equation
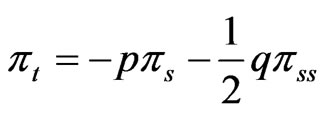
and also the Kolmogorov forward equation
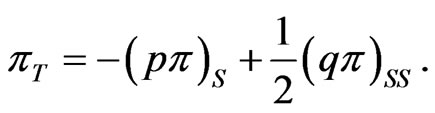 (11)
(11)
The conditions for these results are also set out in the Appendix.
The critical implication of 9 is that 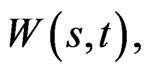 and therefore
and therefore 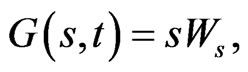 is completely determined by the terminal wealth
is completely determined by the terminal wealth 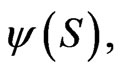 along with an initial condition, say
along with an initial condition, say 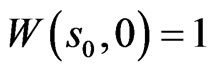 for some initial stock price
for some initial stock price 
In addition, since  satisfies the similar PDE in 7, we have:
satisfies the similar PDE in 7, we have:
 (12)
(12)
where the expectation 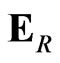 is taken with respect to the process:
is taken with respect to the process:

and

This implies that 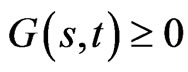 if
if 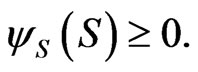
Optimization
Thus for the utility function 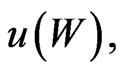 it suffices to find
it suffices to find  so as to maximize:
so as to maximize:

Here the expectation 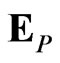 and density
and density 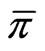 relate to the physical stock process:
relate to the physical stock process:

rather than to 10.
This is subject to the initial condition:
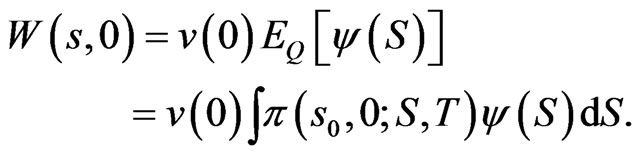
where the expectation  is subject to the risk neutral process in 10.
is subject to the risk neutral process in 10.
The Lagrangian is
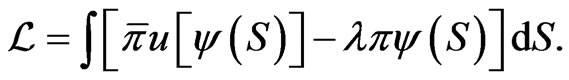
Let  be a variation in
be a variation in  The resulting variation in
The resulting variation in  is, to the second order:
is, to the second order:

Since 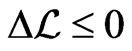 for any variations
for any variations  the first order condition is
the first order condition is

where 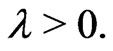 Thus given
Thus given  the function
the function  may be found from
may be found from
 (14)
(14)
with  being chosen to satisfy the initial condition 13.
being chosen to satisfy the initial condition 13.
The second order condition is  so that a concave utility is required. The general solution for
so that a concave utility is required. The general solution for  in terms of
in terms of  is then given by 9. In the general case with
is then given by 9. In the general case with  not constant, we thus have the following extension of the existential results of Proposition 3 of [1]:
not constant, we thus have the following extension of the existential results of Proposition 3 of [1]:
Proposition 3 A path independent strategy  can be found to optimize a given concave utility
can be found to optimize a given concave utility  if, and only if, a solution
if, and only if, a solution  can be found to satisfy:
can be found to satisfy:
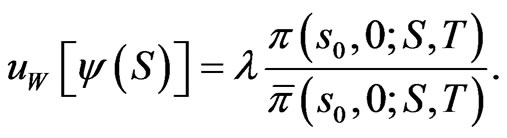
Remark: This is without qualification as to the existence of a solution to 8. In the case that  is given, the Inada conditions provide that
is given, the Inada conditions provide that 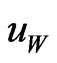 is invertible on
is invertible on 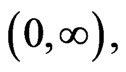 so that
so that

In the case that  is given, the condition
is given, the condition 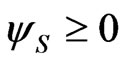 is sufficient to determine
is sufficient to determine  However none of these conditions is mentioned in Proposition 3 of [1].
However none of these conditions is mentioned in Proposition 3 of [1].
Example: [1] assume constant returns and volatilities 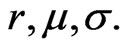 In this case, it is well known that
In this case, it is well known that 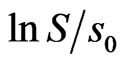 is normally distributed, with mean
is normally distributed, with mean
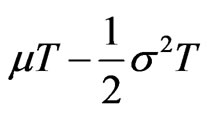
(physical measure) or

(risk neutral measure), and variance 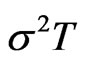 at time
at time 
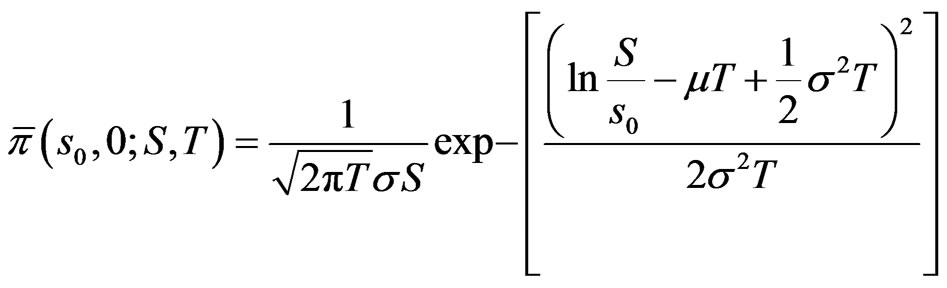
while
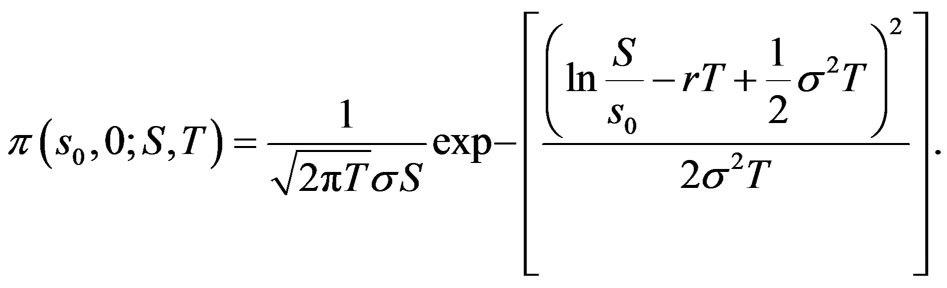
Hence 14 becomes:

Differentiating with respect to 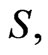 we also have
we also have

Thus  when
when  and vice versa.
and vice versa.
By virtue of 12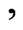 depending on whether
depending on whether 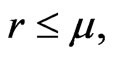 we have a proof of Proposition 3 of [1].
we have a proof of Proposition 3 of [1].
5. Extension of Utility Characterization
It is of interest to consider whether the allocation to the risky asset 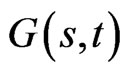 is non-negative under more general conditions than indicated in Proposition 3 of [1].
is non-negative under more general conditions than indicated in Proposition 3 of [1].
Proposition 4 Suppose  are non-stochastic (i.e. independent of
are non-stochastic (i.e. independent of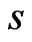 ) and
) and . Then a strategy
. Then a strategy  can be found to optimize a concave utility
can be found to optimize a concave utility 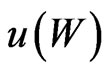 with
with 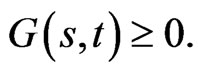
Proof. Given 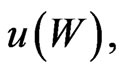 the strategy
the strategy 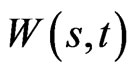 is given by 14 and the Kac-Feynman formula 9. We also note the relation 12, which shows that
is given by 14 and the Kac-Feynman formula 9. We also note the relation 12, which shows that 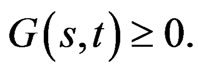 if
if 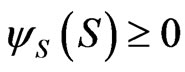 at time
at time 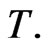
Differentiating 14 with respect to  we have:
we have:
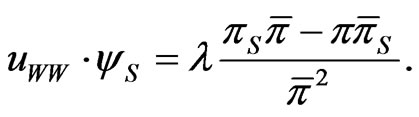
Since 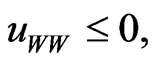 it suffices to show that
it suffices to show that  The variant of Girsanov’s theorem, as proved in the Appendix, confirms this result.
The variant of Girsanov’s theorem, as proved in the Appendix, confirms this result.
Remark: The conditions are sufficient, but by no means necessary. The Appendix shows that the density 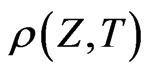 of the risk neutral process for
of the risk neutral process for 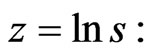
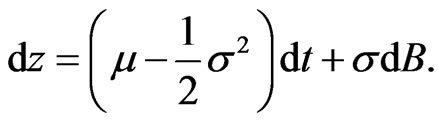
with stochastic 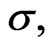 is central to this issue. In particular, if the risk premium
is central to this issue. In particular, if the risk premium 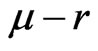 is non-stochastic, and
is non-stochastic, and 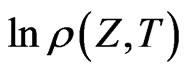 is concave in
is concave in  then the result also holds. This situation may be investigated by noting that
then the result also holds. This situation may be investigated by noting that  satisfies a parabolic PDE, which can in turn be investigated by the eigenfunctions of the operator
satisfies a parabolic PDE, which can in turn be investigated by the eigenfunctions of the operator
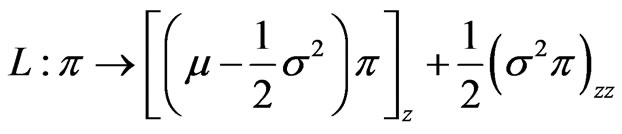 .
.
6. Constrained Strategies
The above discussion does not constrain the allocations to both the risky asset and the riskless asset to be nonnegative, which is often a requirement in practice. For this to apply, we have the additional constraints on terminal wealth:
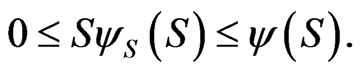
If 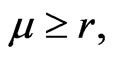 then Proposition 4 provides conditions for
then Proposition 4 provides conditions for  To provide that
To provide that  we need to have the terminal condition:
we need to have the terminal condition:
 (15)
(15)
If this holds, and 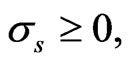 then Equation (12) implies:
then Equation (12) implies:
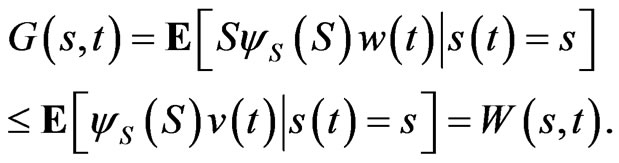
To ensure that 15 holds, consider the Lagrangian:

Let 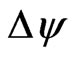 be a variation in
be a variation in  such that
such that 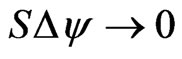 when
when 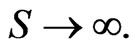 The variation in
The variation in  is, to the second order:
is, to the second order:
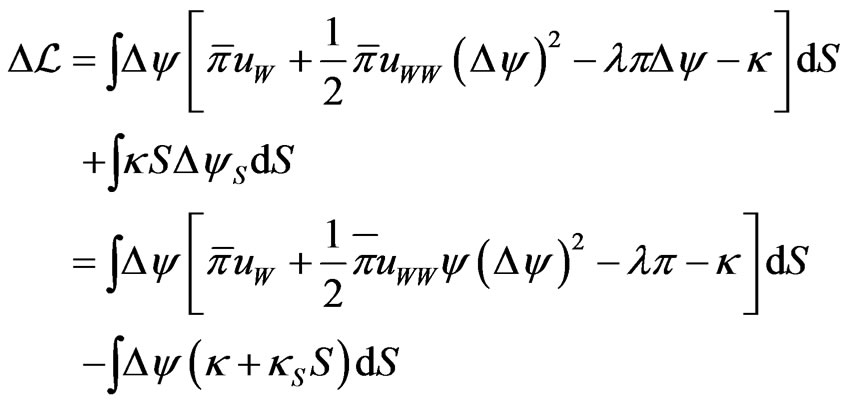
The first order condition is thus:
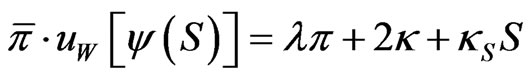
which can be written:

and thus integrating over 

The second order condition is as before:

This leads to the following result:
Proposition 5: Given a concave utility 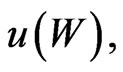 and
and  the strategy
the strategy 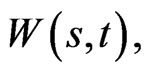 given by the KacFeynman formula 9, provides optimality over nonnegative allocations to the riskless asset, only if there is a solution
given by the KacFeynman formula 9, provides optimality over nonnegative allocations to the riskless asset, only if there is a solution 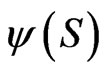 of:
of:

for some 
Remark: These are weaker conditions than provided in Proposition 3, as we are seeking optimality over a smaller class of allocations. Even weaker conditions may be found if the class of allocations is restricted to where both the risky and riskless assets are constrained to be non-negative.
7. Allowance for Cash Flows
The previous relations can be extended to accommodate portfolios with cash withdrawals. Let us now consider the situation when an investor is allowed to withdraw from their investment, at a rate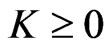 . Such as before, we discuss the cash withdrawn from the portfolio in two cases, a function of price of the risky asset and time,
. Such as before, we discuss the cash withdrawn from the portfolio in two cases, a function of price of the risky asset and time,  , or a function of total wealth and time,
, or a function of total wealth and time,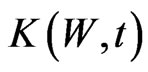 .
.
Total wealth 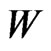 then obeys the generalised relation:
then obeys the generalised relation:
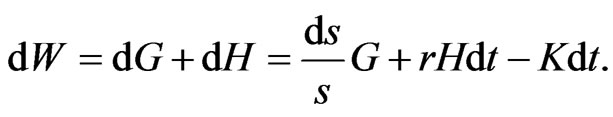
7.1. Controls That Are Functions of the Value of the Risky Asset and Time
In analogy with section 2 consider the case where the controls,  ,
,  and
and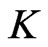 , are all functions of
, are all functions of , where the process of
, where the process of  is the same as in 1.
is the same as in 1.
Allowing for cash withdrawals, 2 generalizes to
 (16)
(16)
This implies that
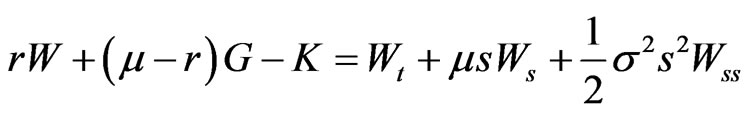 (17)
(17)
and the same condition as in 4, which is consistent with Proposition 1 of [1] that

and hence 5 generalizes to:
 (18)
(18)
It may be shown similarly that 7 generalizes to:
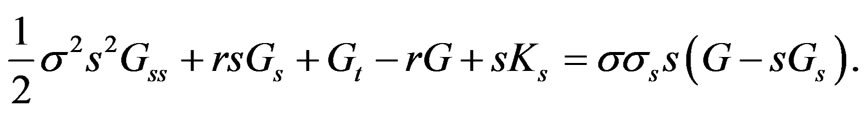 (19)
(19)
Now we can formalize the above results as:
Proposition 6: Necessary and sufficient conditions for the differentiable functions ,
,  and
and  to be the controls of a self-financing investment strategy are that:
to be the controls of a self-financing investment strategy are that:
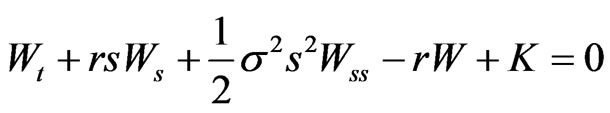 (20)
(20)

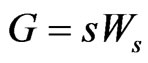 (21)
(21)
for all 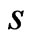 and
and .
.
Notice that Proposition 1 of [1] is a special case of this generalized form with a constant diffusion for price of the risky asset, that is .
.
7.2. Controls That Are Functions of the Value of the Portfolio Wealth and Time
In analogy with section 3, consider the situation when the controls, 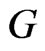 and
and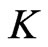 , are functions of
, are functions of .
.
As  is a control, we also have:
is a control, we also have:

Then Equation (7) can be shown to generalize to:
Proposition 7: The control 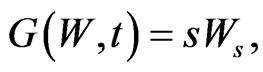 viewed as a function of wealth, satisfies:
viewed as a function of wealth, satisfies:

7.3. Compatibility with Investor Objectives
We now consider if the processes of controls  and
and 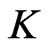 are compatible with rational investor objectives.
are compatible with rational investor objectives.
Express 18 to get
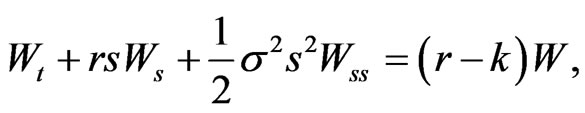
where, without loss of generality, we write

This is again a parabolic PDE in , and the FeynmanKac formula can be applied to find a solution as:
, and the FeynmanKac formula can be applied to find a solution as:
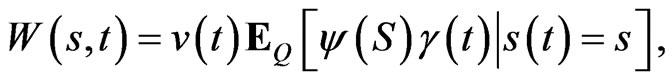 (23)
(23)
but now the discount factor includes:
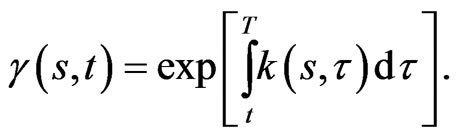
As before, the wealth  is completely determined by the terminal wealth
is completely determined by the terminal wealth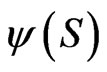 , along with the control
, along with the control 
In the case with cash withdrawals are admissible, we consider not only the utility from terminal wealth for an investor, but also the utility from consumption financed by the cash withdrawals . Therefore, the problem of choosing optimal portfolio and consumption rules for an investor over a period of
. Therefore, the problem of choosing optimal portfolio and consumption rules for an investor over a period of  is to maximize an aggregate utility of the following form:
is to maximize an aggregate utility of the following form:

The function 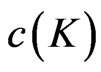 is the utility from consumption, with
is the utility from consumption, with . The initial and terminal times are specified at
. The initial and terminal times are specified at  and
and , as is the initial condition that some initial stock price
, as is the initial condition that some initial stock price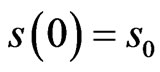 . The expectation
. The expectation  is specified as before in Section 4 for the physical stock process.
is specified as before in Section 4 for the physical stock process.
The Lagrangian is then given by:

This optimization problem is exactly of continuous stochastic control [20, VII.10]. Define an optimal expected value function given the stock price  at time
at time 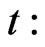

The process terminates at time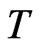 , at which time the utility of terminal wealth is assessed, with the boundary condition
, at which time the utility of terminal wealth is assessed, with the boundary condition
 (24)
(24)
The fundamental PDE for the control 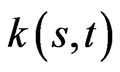 is:
is:
 (25)
(25)
However, we follow an alternative, but simpler, approach. Given 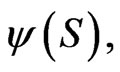 consider a small variation in
consider a small variation in  say
say 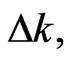 localized at time
localized at time  and in state
and in state 
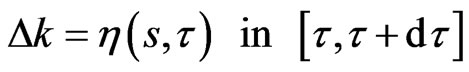
for some constant  which induces a variation
which induces a variation  This further induces variations in the terms
This further induces variations in the terms
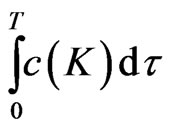
and , to the first order in
, to the first order in :
:

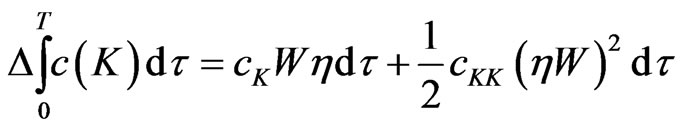
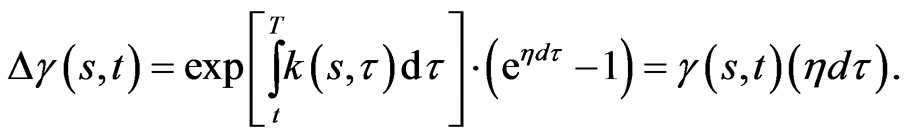
And thus:
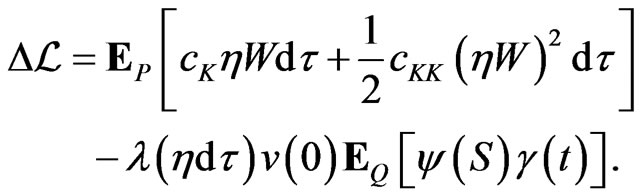
Since 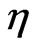 is localized at
is localized at  and
and  is constant, the first order condition in
is constant, the first order condition in  is:
is:

for some constant 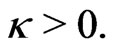
The second order condition in  is:
is:
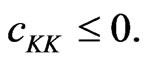
Hence we have the following result.
Proposition 8 Given concave utility functions for terminal wealth  and for consumption
and for consumption , and a terminal wealth with density
, and a terminal wealth with density 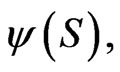 the optimal cash flow control is given by
the optimal cash flow control is given by 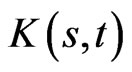 satisfying:
satisfying:
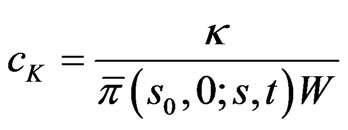 (26)
(26)
for some constant 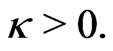
Remark: As  is a decreasing function in
is a decreasing function in  this implies that cash withdrawals should increase in the wealth
this implies that cash withdrawals should increase in the wealth 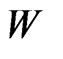 achieved, but should decrease where such wealth is less likely to be achieved. This corresponds to the conditions contained in Proposition 4 of [1].
achieved, but should decrease where such wealth is less likely to be achieved. This corresponds to the conditions contained in Proposition 4 of [1].
8. Conclusions
In this paper, we address two related issues, based on the work by [1].
First, we examine the characteristics of optimal portfolio controls. Rather than assuming constant expected returns and volatility, we consider the more realistic situation with the expected return and volatility of risky assets are non-constant, or even stochastic.
Second, we consider whether a given investment strategy is consistent with expected utility maximization. We apply several techniques of the calculus of variations to show that, under mild conditions, optimal portfolio controls are compatible with some concave utility function. Unlike most papers in the literature, we do not specify a particular form of utility function.
It would be interesting to extend these results to more general asset models, for example where the risky asset follows a jump diffusion process, or where volatility of the return on the risky asset is itself a stochastic process.
REFERENCES
- J. C. Cox and H. E. Leland, “On Dynamic Investment Strategies,” Journal of Economic Dynamics and Control, Vol. 24, No. 11-12, 2000, pp. 1859-1880. http://dx.doi.org/10.1016/S0165-1889(99)00095-0
- R. C. Merton, “Optimum Consumption and Portfolio Rules in a Continuoustime Model,” Journal of Economic Theory, Vol. 3, No. 4, 1971, pp. 373-413. http://dx.doi.org/10.1016/0022-0531(71)90038-X
- F. Black and M. Scholes, “The Pricing of Options and Corporate Liabilities,” The Journal of Political Economy, Vol. 81, No. 3, 1973, pp. 637-654. http://dx.doi.org/10.1086/260062
- J. C. Cox and S. A. Ross, “The Valuation of Options for Alternative Stochastic Processes,” Journal of Financial Economics, Vol. 3, No. 1-2, 1976, pp. 145-166. http://dx.doi.org/10.1016/0304-405X(76)90023-4
- P. Carr, H. Geman and D. Madan, “The Fine Structure of Asset Returns: An Empirical Investigation,” Journal of Business, Vol. 75, No. 2, 2002, pp. 305-332. http://dx.doi.org/10.1086/338705
- S. Hodges and R. Clarkson, “Dynamic Asset Allocation: Insights from Theory,” Philosophical Transactions: Physical Sciences and Engineering, Vol. 347, No. 1684, 1994, pp. 587-598.
- R. C. Merton, “Lifetime Consumption under Uncertaintiy: The Continuous Time Case,” The Review of Economics and Statistics, Vol. 51, No. 3, 1969, pp. 247-257. http://dx.doi.org/10.2307/1926560
- S. A. Ross, “Mutual Fund Separation in Financial Theory—The Separating Distributions,” Journal of Economic Theory, Vol. 17, No. 2, 1978, pp. 254-286. http://dx.doi.org/10.1016/0022-0531(78)90073-X
- G. S. Amin and H. M. Kat, “Hedge Fund Performance 1990-2000: Do the ‘Money Machines’ Really Add Value?” Journal of Financial and Quantitative Analysis, Vol. 38, No. 2, 2003, pp. 251-274. http://dx.doi.org/10.2307/4126750
- S. Vanduffel, A. Chernih, M. Maj and W. Schoutens, “A Note on the Suboptimality of Path-Dependent Pay-Offs in Lévy Markets,” Applied Mathematical Finance, Vol. 16, No. 4, 2009, pp. 315-330. http://dx.doi.org/10.1080/13504860802639360
- S. Kassberger and T. Liebmann, “When Are Path-Dependent Payoffs Suboptimal?” 2009.
- F. C. Klebaner, “Introduction to Stochastic Calculus with Applications,” Imperial College Press, London, 2005. http://dx.doi.org/10.1142/p386
- O. C. Ibe, “Markov Processes for Stochastic Modeling,” Elsevier Academic Press, Waltham, 2009.
- M. J. Brennana, E. S. Schwartz and R. Lagnado, “Strategic Asset Allocation,” Journal of Economic Dynamics and Control, Vol. 21, No. 8-9, 1997, pp. 1377-1403. http://dx.doi.org/10.1016/S0165-1889(97)00031-6
- J. Cvitanic and V. Polimenis, “Optimal Portfolio Allocation with Higher Mo Moments,” Annals of Finance, 2008.
- S. P. Sethi, “A note on Mertons Optimum Consumption and Portfolio Rules in a continuous-Time Model,” Journal of Economic Theory, Vol. 46, No. 2, 1988, pp. 395- 401. http://dx.doi.org/10.1016/0022-0531(88)90138-X
- A. Meucci, “Review of Dynamic Allocation Strategies: Utility Maximization, Option Replication, Insurance, Drawdown Control, Convex-Concave Management,” 2010.
- K. Tanaka, “Dynamic Asset Allocation under Stochastic Interest Rate and Market Price of Risk,” 2009.
- C. Chiarella, C. Hsaio and W. Semmler, “Intertemporal Investment Strategies under Inflation Risk,” University of Technology, Sydney, 2007.
- S. E. Dreyfus, “Dynamic Programming and the Calculus of Variations,” Academic Press, Norwell, 1965.
- S. Janson and J. Tysk, “Feynman-Kac Formulas for BlackScholes Type Operators,” Bulletin London Mathematical Society, Vol. 38, No. 2, 2006, pp. 269-282. http://dx.doi.org/10.1112/S0024609306018194
1. Appendix: Conditions for Known Results
Let a general stochastic process be defined by
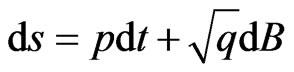
where  and
and 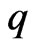 are functions of
are functions of 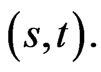 Let
Let 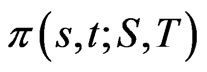 denote the density of
denote the density of  at time
at time 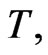 given an initial value of
given an initial value of  Derivatives
Derivatives 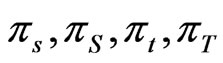 will be taken assuming all other variables are held constant.
will be taken assuming all other variables are held constant.
We summarize various conditions on  and
and  for results to hold. Most of these are cited from [12] and the references therein.
for results to hold. Most of these are cited from [12] and the references therein.
1.1. Conditions
C1  are globally bounded above.
are globally bounded above.
C2 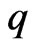 is globally bounded from zero across
is globally bounded from zero across 
C3 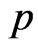 and
and 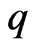 satisfy a global Hölder condition, that is for some parameters
satisfy a global Hölder condition, that is for some parameters  and
and 
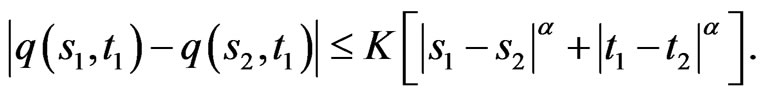
C4  and satisfy a global Hölder condition with respect to
and satisfy a global Hölder condition with respect to 
C5  and the second derivatives with respect to
and the second derivatives with respect to 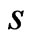 are of most polynomial growth.
are of most polynomial growth.
C6 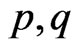 are locally Lipschitz.
are locally Lipschitz.
C7 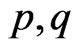 are of at most linear growth.
are of at most linear growth.
C8 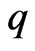 is continuous in
is continuous in 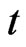 and locally Lipschitz in
and locally Lipschitz in 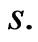
C9  is uniformly bounded and locally Hölder.
is uniformly bounded and locally Hölder.
1.2. Kolmogorov Forward Equation
The probability density  satisfies the Kolmogorov forward equation (11):
satisfies the Kolmogorov forward equation (11):

This holds under the following conditions [12, Theorem 5.15].
• C1.
• C2.
• C3.
1.3. Kolmogorov Backward Equation
The density  considered as a function of
considered as a function of  also satisfies the Kolmogorov backward equation
also satisfies the Kolmogorov backward equation

This holds under the following conditions [12, Theorem 5.15]:
• C1.
• C2.
1.4. Feynman-Kac Formula
Consider the Equation (5), regarded as a parabolic partial differential equation:
 (27)
(27)
where  are functions of
are functions of  as in 5. This is subject to the boundary condition
as in 5. This is subject to the boundary condition 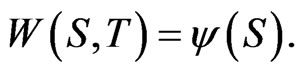 In this section, we allow
In this section, we allow  to be a function of both
to be a function of both 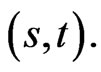
The solution is given by the Feynman-Kac formula, expressed as a stochastic expectation:
 (28)
(28)
where 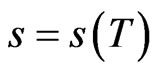 and
and 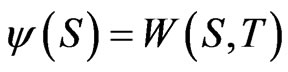 for a given value of
for a given value of  and
and
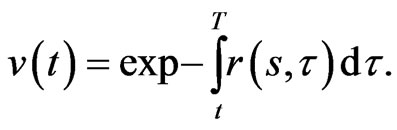
The function 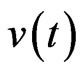 may be regarded as a generalized discount function for interest.
may be regarded as a generalized discount function for interest.
The Feynman-Kac formula holds under the following conditions:
1) (C5), (C6), (C7) and  and
and 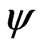 and its derivatives are of at most polynomial growth [12, Theorem 6.2].
and its derivatives are of at most polynomial growth [12, Theorem 6.2].
2) (C7), (C8), (C9) and 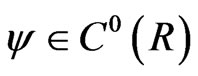 and is of at most polynomial growth [21, Theorem 5.5].
and is of at most polynomial growth [21, Theorem 5.5].
2. Girsanov’s Theorem
Both the physical process 1 and risk-neutral process 10 for 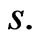 can be simplified under Itô’s lemma by making the transformation
can be simplified under Itô’s lemma by making the transformation 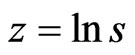 Thus in logarithmic terms the physical process can be described by:
Thus in logarithmic terms the physical process can be described by:
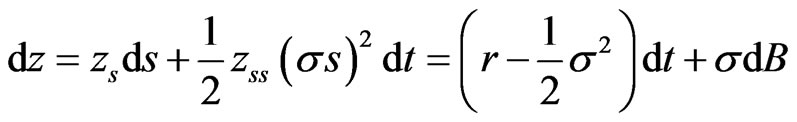
and the physical process by:
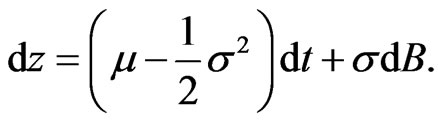
Where 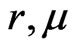 and
and 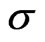 are non-stochastic, with
are non-stochastic, with 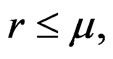 this provides explicit solutions for the physical and risk neutral densities
this provides explicit solutions for the physical and risk neutral densities 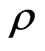 and
and 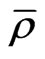 in
in  which obey the forward equations:
which obey the forward equations:
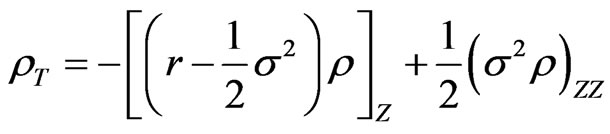 (29)
(29)
and
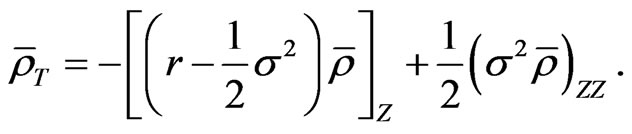 (30)
(30)
For example  is normal with mean
is normal with mean

and variance 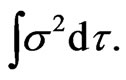 Letting
Letting  and
and
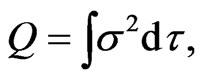
we have
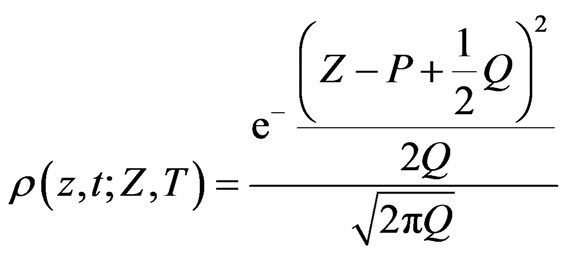
and thus
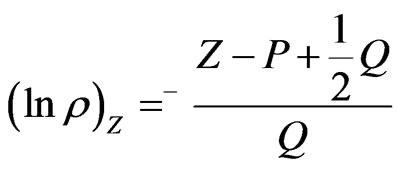 (31)
(31)
On the other hand the density of the stock price  is given by
is given by

with  so that
so that
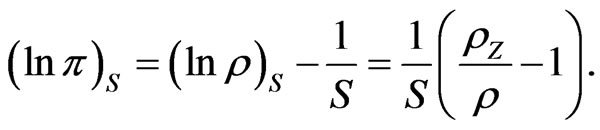
Therefore to show that 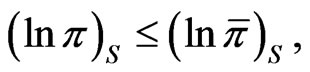 it suffices to show that
it suffices to show that  This can be shown directly from 31. However we take an approach that illustrates a relationship with Girsanov’s theorem, and allows a generalization to the case where the parameters are stochastic.
This can be shown directly from 31. However we take an approach that illustrates a relationship with Girsanov’s theorem, and allows a generalization to the case where the parameters are stochastic.
Make the transformation 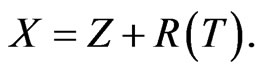 We then have
We then have

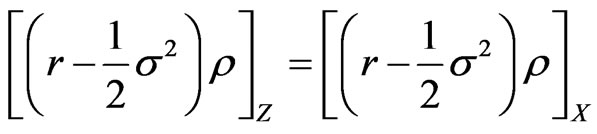
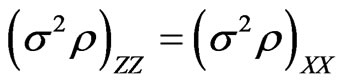
We then have from 29:
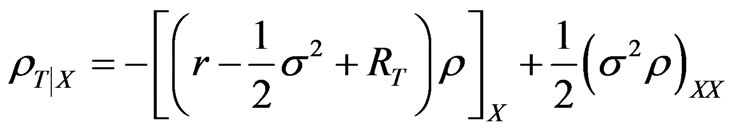
Let 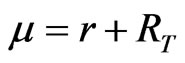 (so that the risk premium
(so that the risk premium 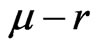 is not stochastic). Then:
is not stochastic). Then:

It may be concluded from comparing this equation with 30 that , so that changing variables:
, so that changing variables:

If  then
then 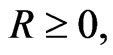 so that
so that 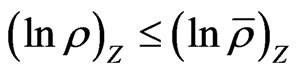 holds if:
holds if:
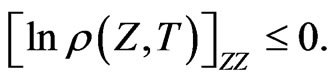
This last condition clearly holds in the case of non-stochastic parameters as in 31. However it is a condition on the risk neutral process only, and may hold in other cases where the stock volatility 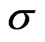 is stochastic.
is stochastic.
NOTES
1We use 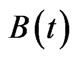 rather than the more conventional
rather than the more conventional 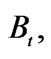 as subscripts in this paper are reserved solely for derivatives.
as subscripts in this paper are reserved solely for derivatives.

