Journal of Mathematical Finance
Vol.3 No.2A(2013), Article ID:30551,8 pages DOI:10.4236/jmf.2013.32A003
Design of Financial Market Regulations against Large Price Fluctuations Using by Artificial Market Simulations*
1SPARX Asset Management Co., Ltd., Tokyo, Japan
2School of Engineering, The University of Tokyo, Tokyo, Japan
3CREST & PRESTO, Japan Science and Technology Agency, Tokyo, Japan
4Faculty of Information Technology, Kanagawa Institute of Technology, Kanagawa, Japan
Email: mizutata@gmail.com
Copyright © 2013 Takanobu Mizuta et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 29, 2013; revised March 6, 2013; accepted March 21, 2013
Keywords: Artificial Market; Multi Agent Simulation; Financial Crash; Price Variation Limit; Short Selling Regulation; Up-Tick Rule
ABSTRACT
We built an artificial market model and compared effects of price variation limits, short selling regulations and up-tick rules. In the case without the regulations, the price fell to below a fundamental value when an economic crush occurred. On the other hand, in the case with the regulations, this overshooting did not occur. However, the short selling regulation and the up-tick rule caused the trading prices to be higher than the fundamental value. We also surveyed an adequate limitation price range and an adequate limitation time span for the price variation limit and found a parameters’ condition of the price variation limit to prevent the over-shorts. We also showed the limitation price range should be bigger than a volatility calculated by the limitation time span.
1. Introduction
Financial exchanges sometimes employ a “price variation limit”, which restrict trades out of certain price ranges within certain time spans to avoid sudden large price fluctuations. For example, Tokyo Stock Exchange employs two kinds of price variation limits that adopt different time spans: one is “daily price limit” which restricts price fluctuations within a single trading day, and the other is “special quote”, which restricts within three minutes [1]. Most Asian stock exchanges (Tokyo, Taipei, Shanghai, Shenzhen, Seoul, and so on) employ the price variation limits, but many American and European stock exchanges do not because there is a debate over whether the price variation limit makes financial market more efficient or not. On financial markets, other regulations, “short selling regulation”1, “up-tick rule”2 and so on, also are debated over whether makes more efficient or not.
| 3Excellent reviews are [2,3]. |
Because so many factors cause price formation in actual markets, an empirical study can not isolate a pure contribution of these regulations to price formation. Therefore, it is very difficult to discuss about a pure effect of these regulations only by results of empirical studies. An artificial market3 which is a kind of an agent based simulation will help us to discuss about this very well. There are several previous studies to discuss about regulations of financial market using artificial market simulations. Yagi et al. investigated effect of short selling regulations induce bubbles [4,5]. Westerhoff discussed effectiveness of transaction taxes, central bank interventions and trading halts [6]. Thurner et al. showed that as leverage increases price fluctuation becomes heavy tailed and display clustered volatility [7]. Kobayashi and Hashimoto showed that circuit breakers play an important role in controlling price fluctuations, while they also reduce the trading volume [8]. Yeh and Yang investigated the effectiveness of price variation limits and showed that price variation limits help to reduce volatility and price distortion [9]. Mizuta et al. discussed effectiveness of price variation limits and argued that an artificial market model testing such regulations should be implementing a learning process to replicate bubbles, and showed that a hazard rate enables verification of whether the models can replicate a bubble process or not [10]. However, no simulation studies have investigated up-tick rules, and compared effects of the short selling regulation, the up-tick rule and the price variation limit using an artificial market model. These regulations are expected to be especially effective to prevent bubbles and crushes, so simulation studies investigating these regulations should use artificial market models replicating bubbles and crushes.
We built an artificial market model and compared effects of price variation limits, short selling regulations and up-tick rules. In the case without the regulations, the price fell to below a fundamental value when an economic crush occurred. On the other hand, in the case with the regulations, this overshooting did not occur. However, the short selling regulation and the up-tick rule caused the trading prices to be higher than the fundamental value. We also surveyed an adequate limitation price range and an adequate limitation time span for the price variation limit and found a parameters’ condition of the price variation limit to prevent the over-shorts. We also showed the limitation price range should be bigger than a volatility calculated by the limitation time span. The paper is structured as follows; in section 2, we explain details of our artificial market model. In section 3, we show results of simulations. The paper’s conclusions are presented in section 4.
2. Artificial Market Model
We built a simple artificial market model on the basis of the model of [11]. The model treats only one risk asset and non-risk asset (cash) and adopts a continuous double auction4 to determine a market price of the risk asset. The number of agents is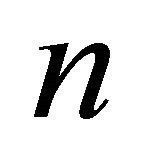 . At first, at time
. At first, at time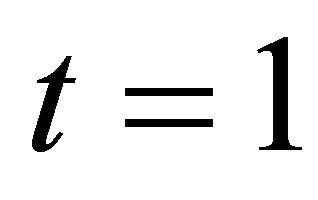 , an agent 1 orders to buy or sell the risk asset; after that at
, an agent 1 orders to buy or sell the risk asset; after that at 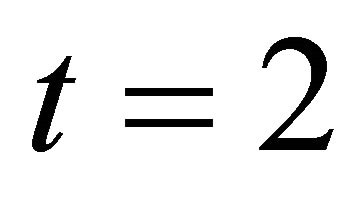 an agent 2 orders; at
an agent 2 orders; at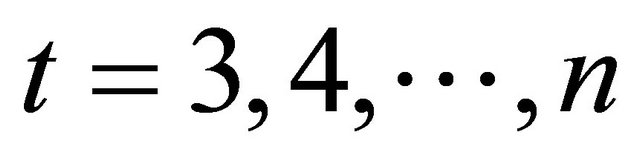 , an agent
, an agent  orders respectively. At
orders respectively. At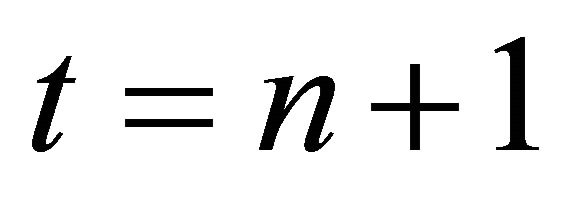 , going back to the first, the agent 1 orders, and at
, going back to the first, the agent 1 orders, and at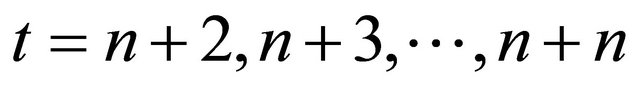 , an agent
, an agent 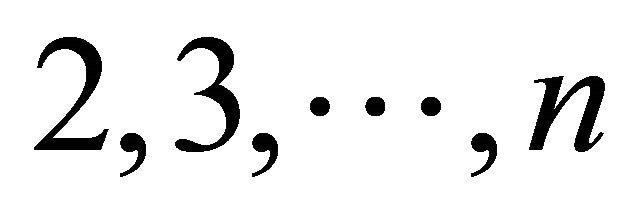 orders respectively, and this cycle is repeated. Note that time
orders respectively, and this cycle is repeated. Note that time  passes even if no deals are done. An agent
passes even if no deals are done. An agent  determines an order price and buys or sells by the following process. Agents use a combination of fundamental value and technical rules to form expectations on a risk asset returns. An expected return of the agent
determines an order price and buys or sells by the following process. Agents use a combination of fundamental value and technical rules to form expectations on a risk asset returns. An expected return of the agent  is
is
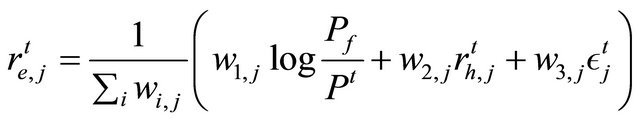 , (1)
, (1)
where  is weight of term
is weight of term  of the agent
of the agent , and is determined by random variables of uniformly distributed in the interval
, and is determined by random variables of uniformly distributed in the interval 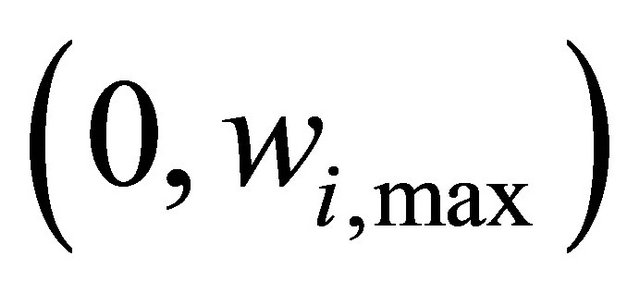 at the start of the simulation independently for each agent.
at the start of the simulation independently for each agent. 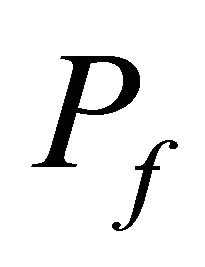 is a fundamental value that is constant.
is a fundamental value that is constant.  is a market price of the risk asset at time
is a market price of the risk asset at time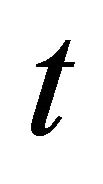 . (When the dealing is not done at
. (When the dealing is not done at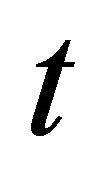 ,
, 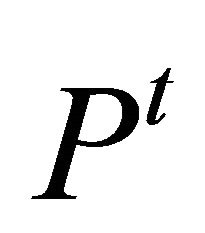 remains at the last market price
remains at the last market price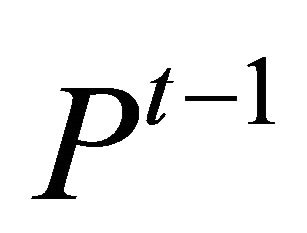 , and at
, and at ,
,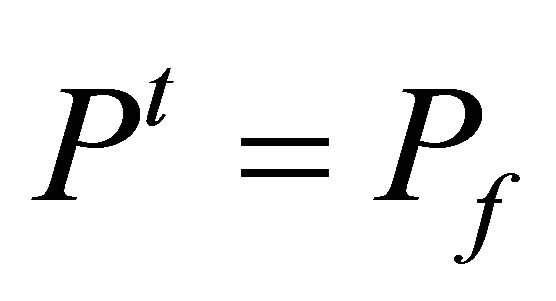 ).
). 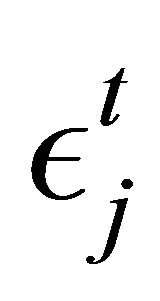 is a noise determined by random variables of normal distribution with an average 0 and a variance
is a noise determined by random variables of normal distribution with an average 0 and a variance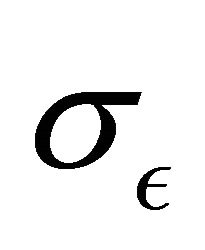 .
. 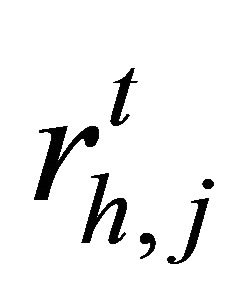 is a historical price return inside an agent’s time interval
is a historical price return inside an agent’s time interval , and
, and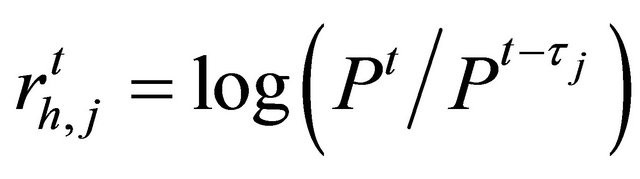 .
. 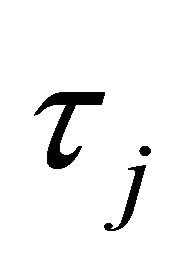 is determined by random variables uniformly distributed in the interval
is determined by random variables uniformly distributed in the interval 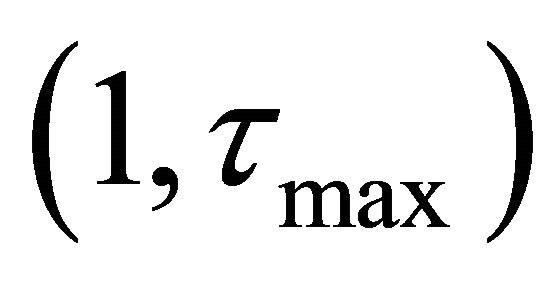 at the start of the simulation independently for each agent. The first term of Equation (1) represents a fundamental strategy: an agent expects a positive return when the market price is lower than the fundamental value, and vice verse. The second term of Equation (1) represents a technical strategy: an agent expects a positive return when historical market return is positive, and vice verse. After the expected return has been determined, an expected price is
at the start of the simulation independently for each agent. The first term of Equation (1) represents a fundamental strategy: an agent expects a positive return when the market price is lower than the fundamental value, and vice verse. The second term of Equation (1) represents a technical strategy: an agent expects a positive return when historical market return is positive, and vice verse. After the expected return has been determined, an expected price is
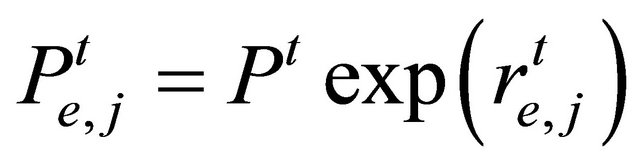 . (2)
. (2)
We modeled an order price 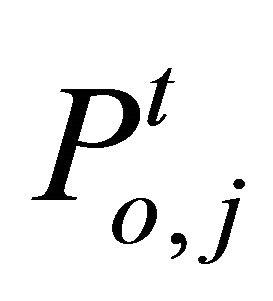 by random variables of uniformly distributed in the interval
by random variables of uniformly distributed in the interval  , where
, where  is a constant. A minimum unit of a price change (tick size) is
is a constant. A minimum unit of a price change (tick size) is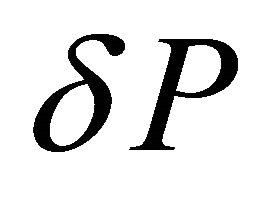 , we round off a fraction of less than
, we round off a fraction of less than . Buy or sell is determined by a magnitude relation between the expect price
. Buy or sell is determined by a magnitude relation between the expect price  and the order price
and the order price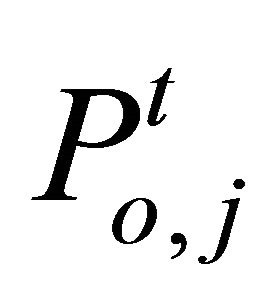 , that isWhen
, that isWhen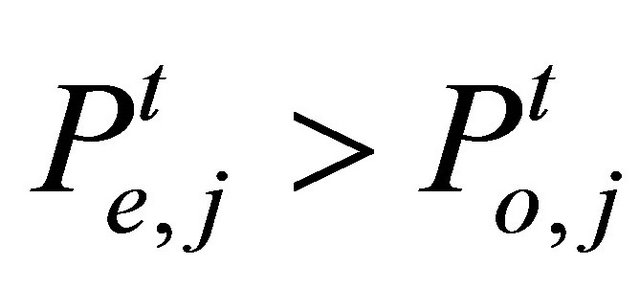 , the agent orders to buy one share.
, the agent orders to buy one share.
When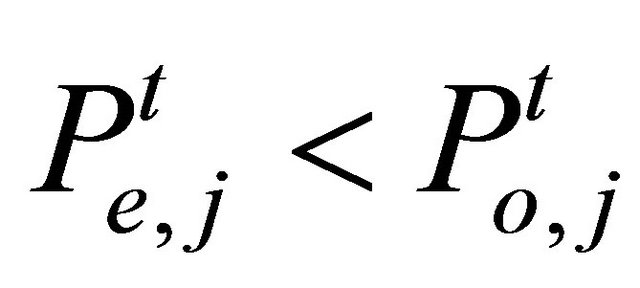 , the agent orders to sell one share.
, the agent orders to sell one share.
Agents always order only one share. Our model adopts the continuous double auction, so when an agent orders to buy (sell), if there is a lower price sell order (a higher price buy order) than the agent’s order, dealing is immediately done. If there is not, the agent’s order remains in the order book. The remaining order is canceled at 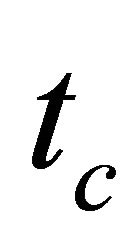 after the order time. Agents can short selling freely. The quantity of holding positions is not limited, so agents can take any shares for both long and short positions to infinity.
after the order time. Agents can short selling freely. The quantity of holding positions is not limited, so agents can take any shares for both long and short positions to infinity.
We also developed a model implementing a learning process of agents. Every agent learns just before every ordering. If there is only the first term (representing a fundamental strategy) or second term (representing a technical strategy) in Equation (1), an expected return 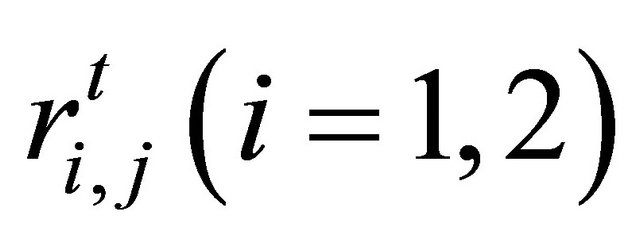 at time
at time  of an agent
of an agent  is
is
 , (3)
, (3)
respectively. We define 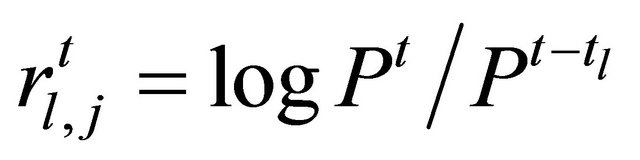 where
where  is a constant evaluation term.
is a constant evaluation term. 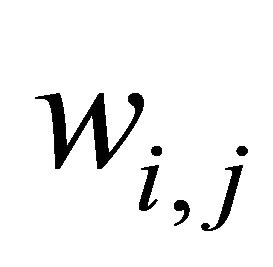 is changed when both
is changed when both 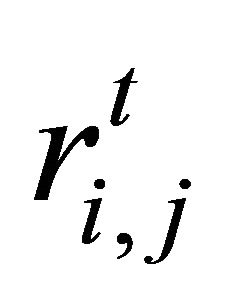 and
and 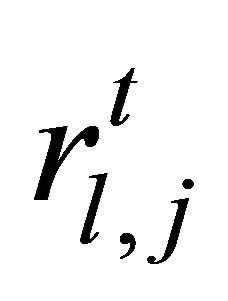 are the same signs,
are the same signs,
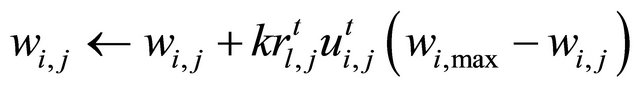 , (4)
, (4)
On the other hand, when both  and
and  are opposite signs,
are opposite signs,
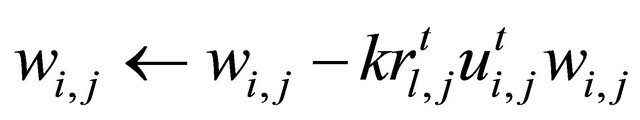 , (5)
, (5)
where 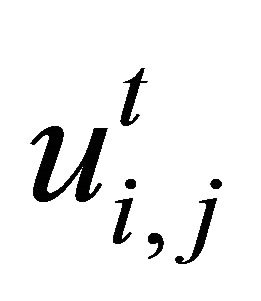 is random variables of uniformly distributed in the interval (0,1) for each
is random variables of uniformly distributed in the interval (0,1) for each ,
,  is constant. Besides this process,
is constant. Besides this process, 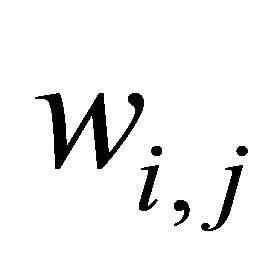 is reset, random variables of uniformly distributed in the interval
is reset, random variables of uniformly distributed in the interval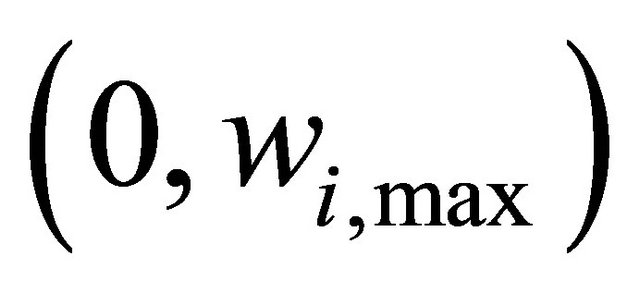 , occurring with small probability,
, occurring with small probability, . In this way, agents learn better parameters and switch to the investment strategy that estimates correctly: the fundamental strategy or technical strategy.
. In this way, agents learn better parameters and switch to the investment strategy that estimates correctly: the fundamental strategy or technical strategy.
We investigated effectiveness of price variation limits, short selling regulations and up-tick rules. In this study, we modeled these regulations as follows. Price variation limits were modeled that any agents can freely order a price from  to
to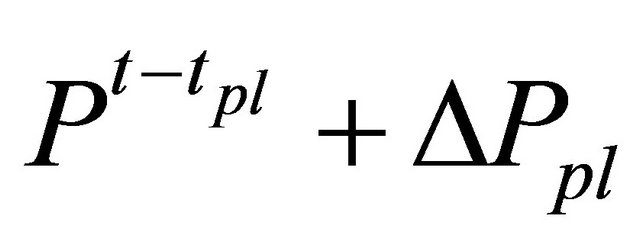 , where
, where 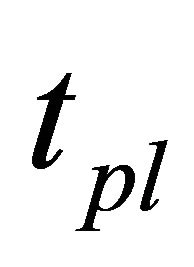 is a constant time span, and
is a constant time span, and 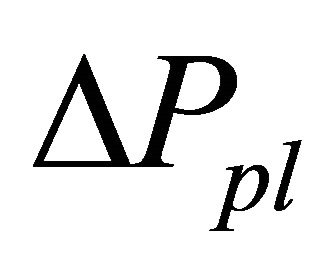 is a constant price. Any order prices of buy above
is a constant price. Any order prices of buy above 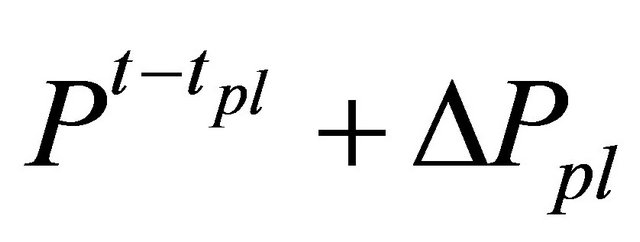 are changed to
are changed to , and any order prices of sell under
, and any order prices of sell under  are changed to
are changed to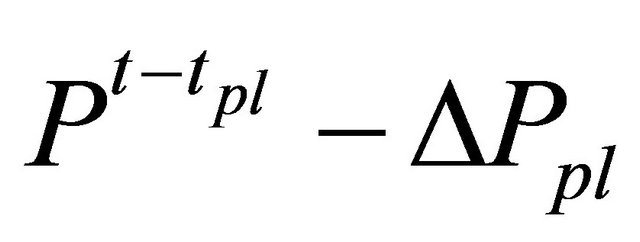 . This prevents trading that prices outside
. This prevents trading that prices outside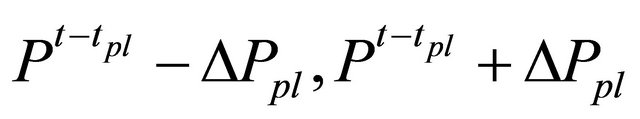 . Short selling regulations were modeled that agents which do not have the risk asset can not order to sell. Any agents have initially one unit risk asset. Up-tick rules were modeled when an agent which do not have the risk asset tries to order to sell a price not greater than
. Short selling regulations were modeled that agents which do not have the risk asset can not order to sell. Any agents have initially one unit risk asset. Up-tick rules were modeled when an agent which do not have the risk asset tries to order to sell a price not greater than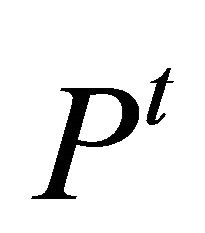 , the order price is changed to
, the order price is changed to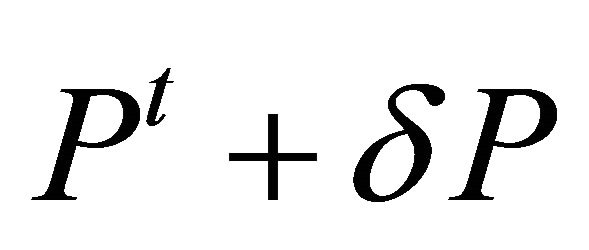 .
.
3. Simulation Result
In this study, we set 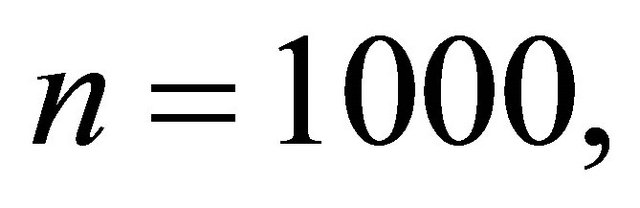
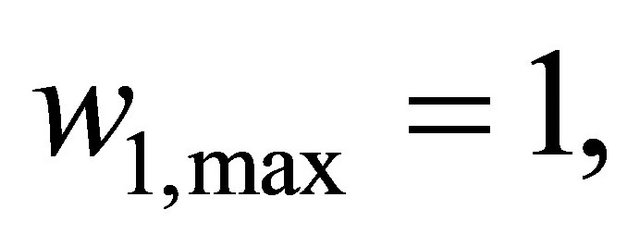
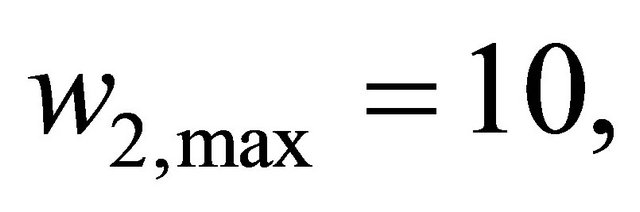
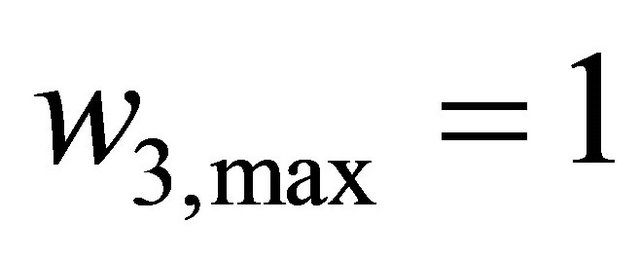 ,
, 

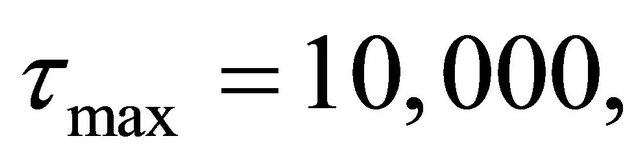

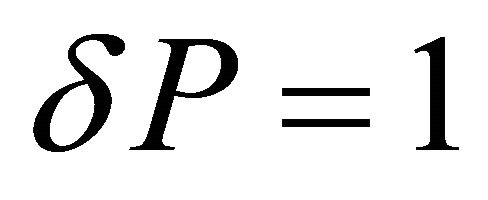 ,
, 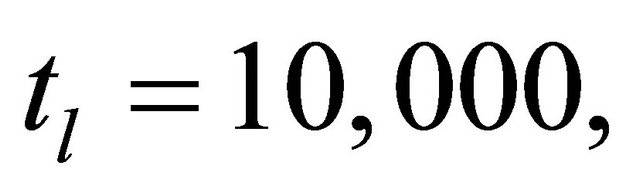
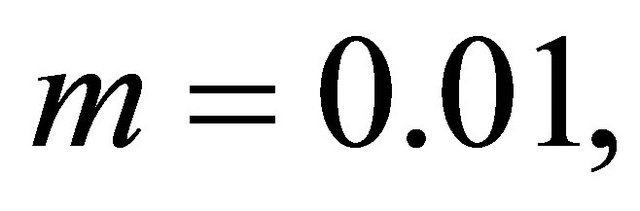
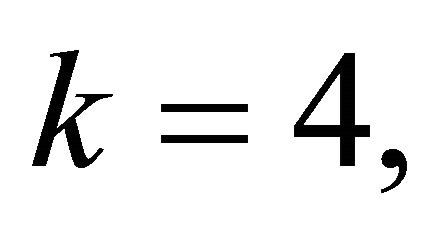
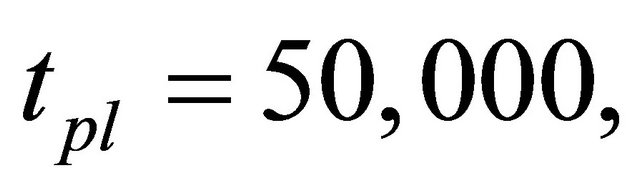
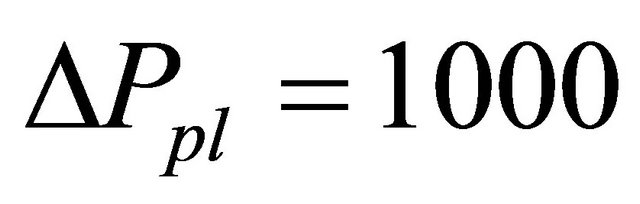 . We also investigated two cases: the fundamental value
. We also investigated two cases: the fundamental value 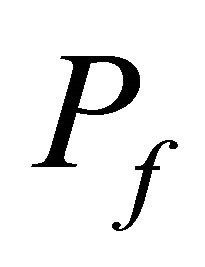 was fixed to 10,000 (constant fundamental value);
was fixed to 10,000 (constant fundamental value);  was 10,000 until
was 10,000 until  and changed to 7000 after
and changed to 7000 after 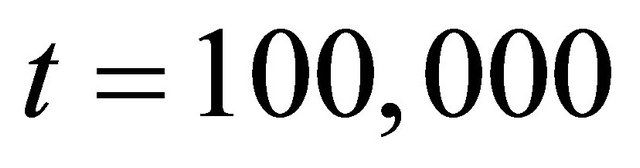 (sharp declining fundamental value). We ran simulations to
(sharp declining fundamental value). We ran simulations to 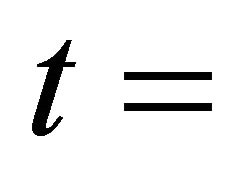
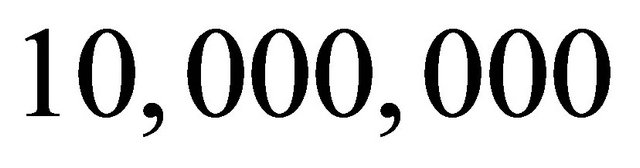 .
.
3.1. Verification the Model
In many previous artificial market studies5, the models are verified to see whether they can explain the stylized facts such as a fat-tail6, volatility-clustering7, and so on. Table 1 lists stylized facts in each case. We used returns for 100 time units’ intervals to calculate the statistical values for the stylized facts8. In all runs, we can find that both kurtosis and autocorrelation coefficients for square returns with several lags are positive, which means that all runs replicate stylized facts.
In the actual financial markets including bubbles (crushes), the probability that a run, sequence of observations of the same sign, of positive (negative) returns will end should decline with the length of the run  [17,18]. A hazard rate
[17,18]. A hazard rate 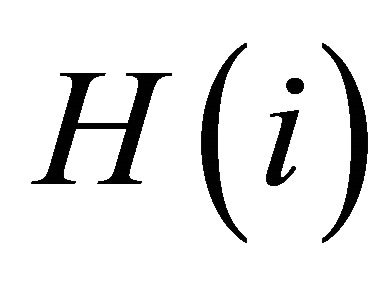 is used for the test of bubbles or crushes.
is used for the test of bubbles or crushes. 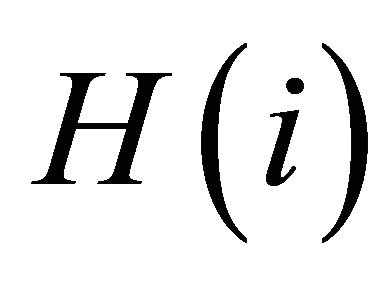 represents the conditional probability that a run ends at
represents the conditional probability that a run ends at , given that it lasts until
, given that it lasts until . Empirical studies show that
. Empirical studies show that 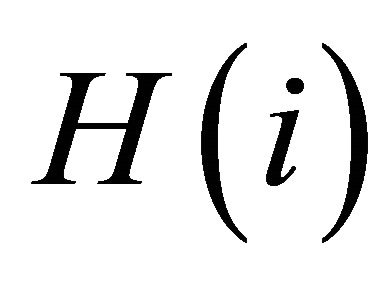 decline with the length of run
decline with the length of run  if observation data include bubble or crush phenomena [17,18]. This means that the bubble (crush) returns tend to continue to be positive (negative) and this tendency becomes stronger as runs of positive (negative) returns become longer. In the Table 1,
if observation data include bubble or crush phenomena [17,18]. This means that the bubble (crush) returns tend to continue to be positive (negative) and this tendency becomes stronger as runs of positive (negative) returns become longer. In the Table 1, 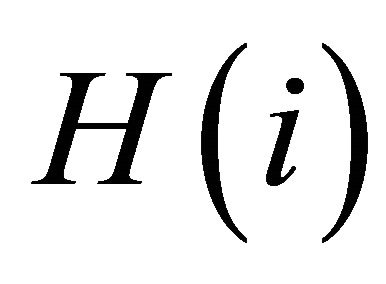 represents the conditional probability that a negative return run ends at
represents the conditional probability that a negative return run ends at , given that it lasts until
, given that it lasts until . When hazard rates
. When hazard rates  declined increasing
declined increasing , the simulation can replicate a significant crush like those occurring in actual markets. In the case of the constant fundamental value with a short selling regulation,
, the simulation can replicate a significant crush like those occurring in actual markets. In the case of the constant fundamental value with a short selling regulation, 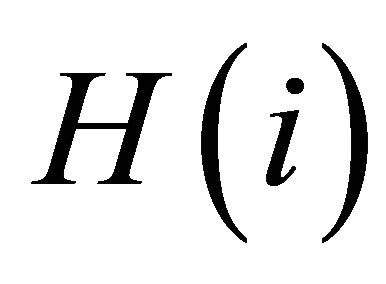 declined. This indicates that some small crushes occurred even though there was no crush-inducing trigger. In the case of the sharp declining fundamental value, except the case of implementing the price variation limit,
declined. This indicates that some small crushes occurred even though there was no crush-inducing trigger. In the case of the sharp declining fundamental value, except the case of implementing the price variation limit,  declined shallowly. These cases replicated big crushes like those occurring in actual markets.
declined shallowly. These cases replicated big crushes like those occurring in actual markets.
3.2. Time Evolutions of Prices
Figure 1 shows time evolution of market prices in the case of the constant fundamental value. In the case without regulations and with the price variation limit, the market prices oscillated around the fundamental value, 10,000. This indicates that the market was efficient. On the other hand, in the case with the short selling regulation, bubbles and crushes occurred repetitively, and the prices were almost higher than the fundamental value. This result is consistent with previous studies [4]9. In the case with the up-tick rule, the prices were almost higher than the fundamental value although the amplitudes are less than those of the case with short selling regulation.
Figure 2 shows time evolution of prices in the fundamental value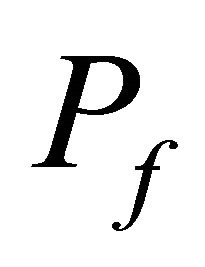 changed at
changed at  from 10,000 to 7000, which was the new fundamental value. In the case
from 10,000 to 7000, which was the new fundamental value. In the case
Table 1. Stylized facts in each run.
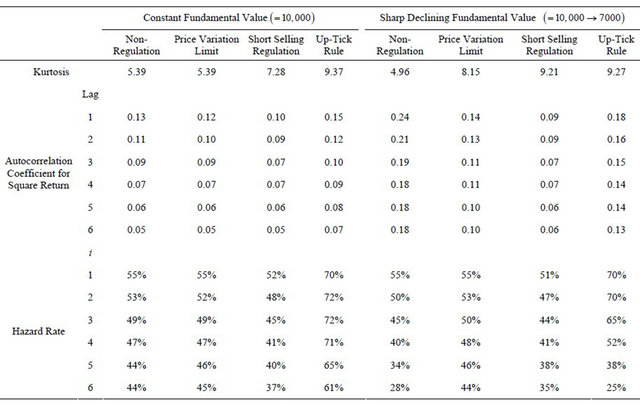
Figure 1. A time evolution of market prices in case that the fundamental value is constant .
.
without regulations, the price went far 6000 beyond the new fundamental value, in other words, an overshoot occurred. After this overshoot, the price rebounded to the new fundamental value. Such the overshoots and re-
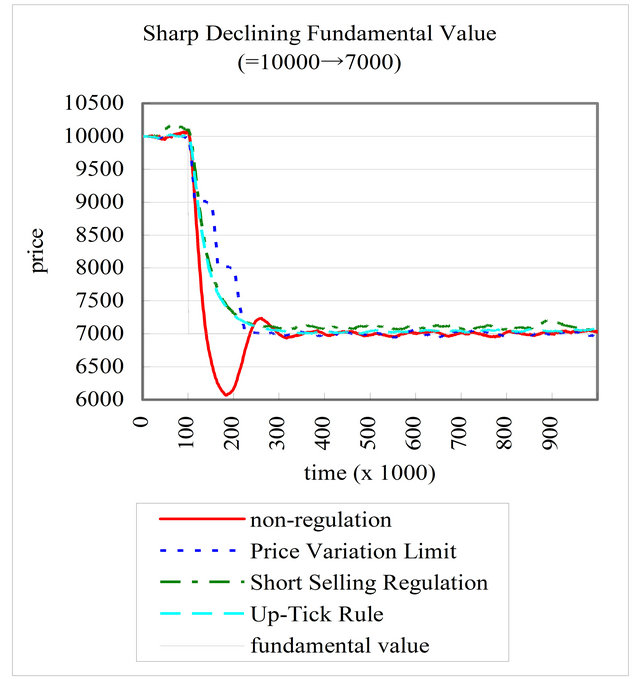
Figure 2. A time evolution of market prices in case that the fundamental value is sharply declining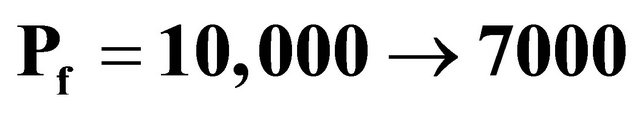 .
.
bounds were investigated by previous studies [19]. On the other hand, in the case with regulations, the price variation limit, the market price took longer to reach the new fundamental price  than in the case without the regulations, but the bubble almost vanished. In the case with the short selling regulation and the uptick rule, small bubbles and crushes occurred repetitively after the prices converged as same when the fundamental values were constants. The price variation limit prevented both such small bubbles and the overshoots. The most efficient market, an ideal market, prevents overshoots and achieves immediate convergence to the new fundamental value. However, this study shows that no market achieves both at once.
than in the case without the regulations, but the bubble almost vanished. In the case with the short selling regulation and the uptick rule, small bubbles and crushes occurred repetitively after the prices converged as same when the fundamental values were constants. The price variation limit prevented both such small bubbles and the overshoots. The most efficient market, an ideal market, prevents overshoots and achieves immediate convergence to the new fundamental value. However, this study shows that no market achieves both at once.
3.3. Switching Strategy
Figures 3 and 4 show a time series of fundamental strategy weights  and technical strategy weights
and technical strategy weights 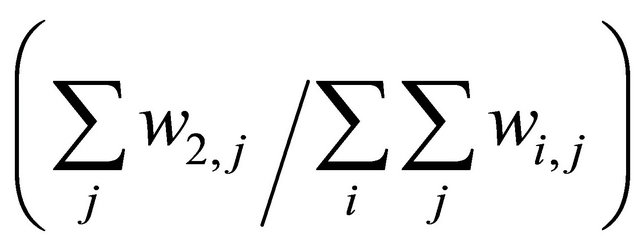 in case of the sharp declining fundamental value, without regulations and with the price variation limit, respectively. Figure 3 shows that, during the crush from about
in case of the sharp declining fundamental value, without regulations and with the price variation limit, respectively. Figure 3 shows that, during the crush from about 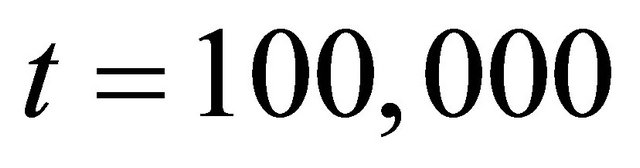 to
to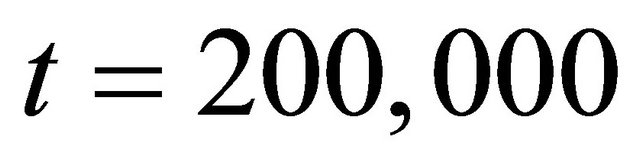 , the technical strategy weight increased and the fundamental strategy weight declined. This is consistent with empirical studies [20,21] that show that investors tend to switch from the fundamental to the technical strategy during a crush because the fundamental strategy looses during an overshoot, declining the price less than the fundamental value. Figure 4" target="_self"> Figure 4 shows that, in contrast to in the case without regulations, during the crush the technical strategy weight did not increase but the fundamental strategy weight did. The price variation limit restricted agents switching to the technical strategy and
, the technical strategy weight increased and the fundamental strategy weight declined. This is consistent with empirical studies [20,21] that show that investors tend to switch from the fundamental to the technical strategy during a crush because the fundamental strategy looses during an overshoot, declining the price less than the fundamental value. Figure 4" target="_self"> Figure 4 shows that, in contrast to in the case without regulations, during the crush the technical strategy weight did not increase but the fundamental strategy weight did. The price variation limit restricted agents switching to the technical strategy and
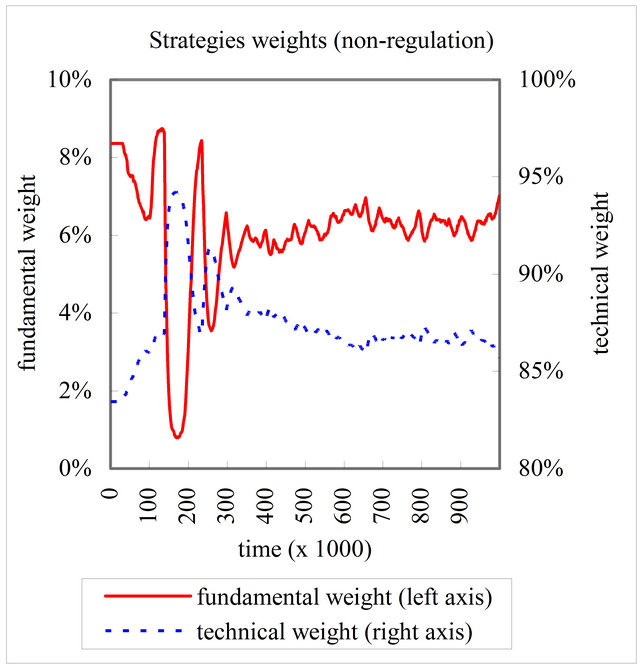
Figure 3. Time series of a fundamental strategy weight and a technical strategy weight in case without any regulations.
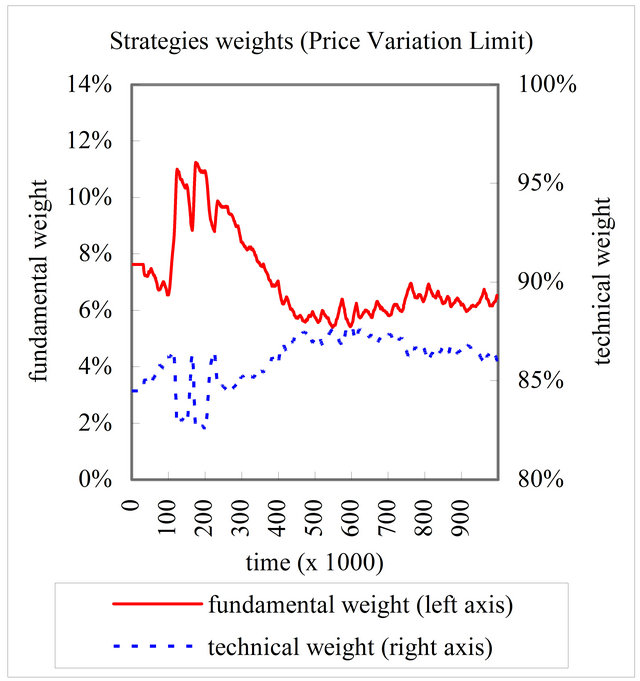
Figure 4. Time series of a fundamental strategy weight and a technical strategy weight in case with the price variation limit.
sprevented overshoots occurring10.
3.4. Survey Adequate Price Limitation
Next, we investigated optimization of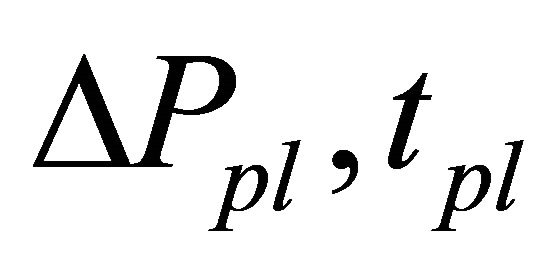 . The price variation limit prevents overshoots but also causes converging speed of market prices to the fundamental value to go slower. The most efficient market, an ideal market, prevents overshoots and achieves immediate convergence to the new fundamental value. However, no market achieves both at once. To make amplitude of an overshoot smaller, market prices converge to fundamental prices more slowly. On the other hand, if you speed up converging speed of market prices to the new fundamental value, occurrence of an overshoot is unavoidable. Therefore, it is important to search for better parameters,
. The price variation limit prevents overshoots but also causes converging speed of market prices to the fundamental value to go slower. The most efficient market, an ideal market, prevents overshoots and achieves immediate convergence to the new fundamental value. However, no market achieves both at once. To make amplitude of an overshoot smaller, market prices converge to fundamental prices more slowly. On the other hand, if you speed up converging speed of market prices to the new fundamental value, occurrence of an overshoot is unavoidable. Therefore, it is important to search for better parameters, 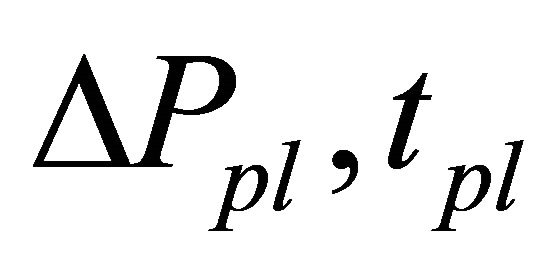 , preventing overshoots and not trying to make the converging speed much slower.
, preventing overshoots and not trying to make the converging speed much slower.
Table 2 lists minimum prices from new fundamental value (max price minus 7000) for various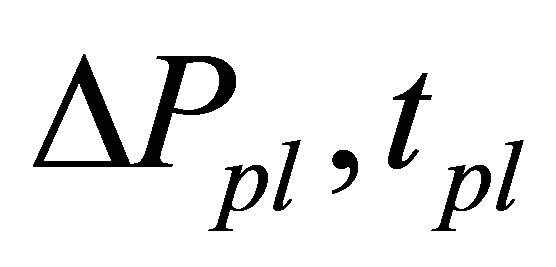 , and Table 3 lists reaching times to new fundamental value divided by 1000 for various
, and Table 3 lists reaching times to new fundamental value divided by 1000 for various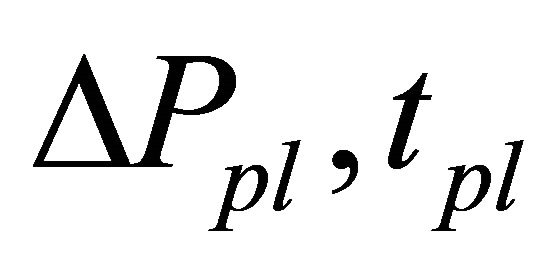 . The reaching times are measured from a time when fundamental value is decreased,
. The reaching times are measured from a time when fundamental value is decreased,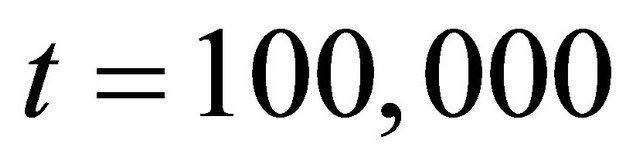 . “--” shows the case where market price could not reach the new fundamental price until
. “--” shows the case where market price could not reach the new fundamental price until . Table 2 indicates that when
. Table 2 indicates that when  is longer and/or
is longer and/or 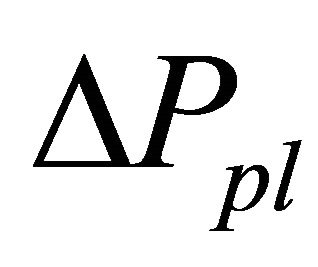 is smaller, overshoots are smaller. On the other hand, Table 3 indicates that when
is smaller, overshoots are smaller. On the other hand, Table 3 indicates that when  is shorter and/or
is shorter and/or 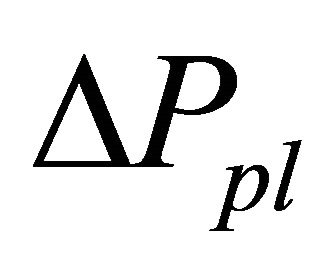 is larger, converging speed to the fundamental value is faster. These tables suggest that the
is larger, converging speed to the fundamental value is faster. These tables suggest that the
Table 2. Minimum prices from new fundamental value for various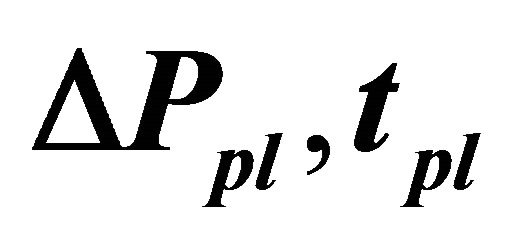 .
.
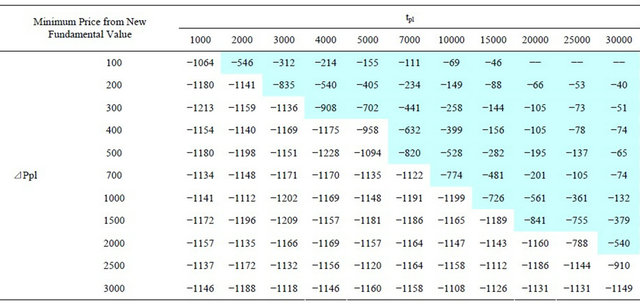
Table 3. Reaching times to new fundamental value divided by 1000 for various .
.
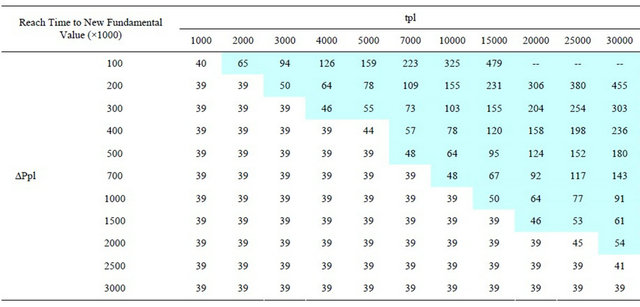
faster convergence to the new fundamental price and the smaller overshoot are not compatible. To make amplitude of a overshoot smaller, market prices converge to fundamental prices more slowly. On the other hand, if you speed up converging speed of market prices to fundamental value, occurrence of an overshoot is unavoidable. In an area of the lower left of Table 3, values are very similar, about 39,000. This value is almost the same as the converging speed to the fundamental value without the price variation limit,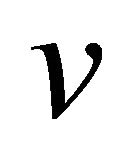 . In the case without the price variation limit, it took about 39,000 for a price to rise to 7000 from 10,000, so
. In the case without the price variation limit, it took about 39,000 for a price to rise to 7000 from 10,000, so 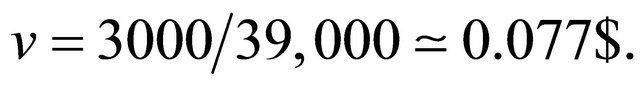 Shadow areas in Tables 2 and 3 satisfy an inequality constraint,
Shadow areas in Tables 2 and 3 satisfy an inequality constraint,
 . (6)
. (6)
Table 2 shows that overshoots did not occur in this shadow area. Therefore, Equation (6) is a condition for the price variation limit to prevent overshoots. In the left term of Equation (6) (further to upper right in these tables) bubbles are smaller but the converging speed slower. In this sense, the market is less efficient. When we design the price variation limit, it is important that the parameters satisfy Equation (6) and the left term is not much smaller than the right term.
Figure 5 showed that several in the same ,
, 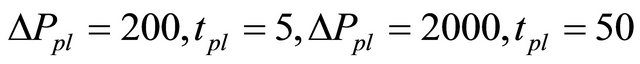 and
and
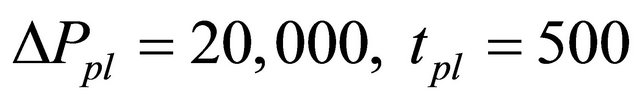 . When
. When 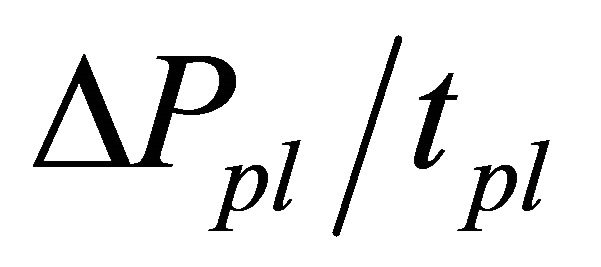 is same, it seemed that the time evolution of market prices tend to be similar from Tables 2 and 3. However, in Figure 5, only in the case of
is same, it seemed that the time evolution of market prices tend to be similar from Tables 2 and 3. However, in Figure 5, only in the case of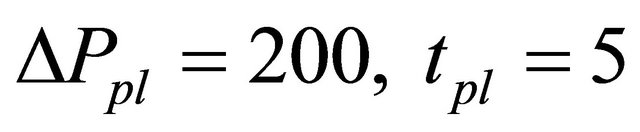 , the market prices declined a little and did never reach to the new fundamental value by the simulation end time,
, the market prices declined a little and did never reach to the new fundamental value by the simulation end time,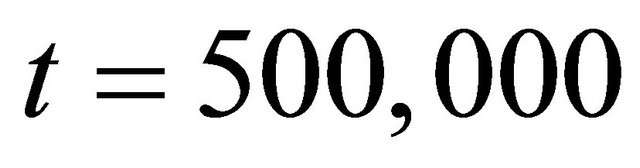 . This implicated that even if
. This implicated that even if 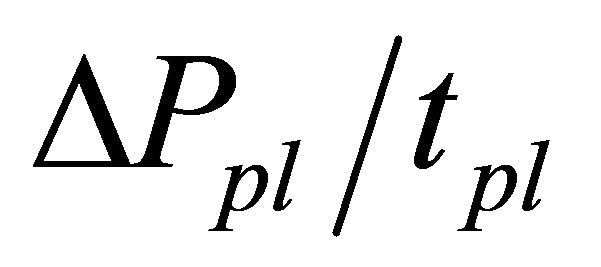 is same, when
is same, when 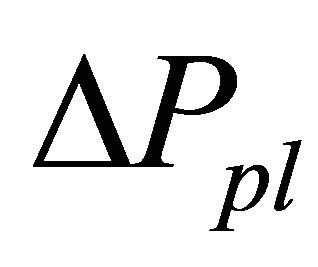 and
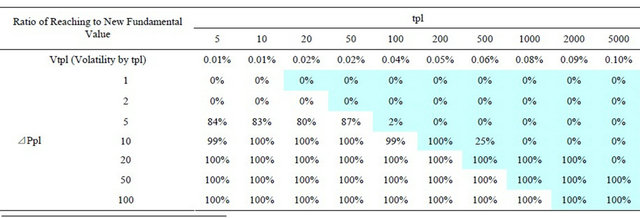
and  are too small, the market become to be inefficient prevented converging to the new fundamental value. Table 4 showed ratios of reaching to new fundamental value by simulation ends to 100 times simulation runs for various small
are too small, the market become to be inefficient prevented converging to the new fundamental value. Table 4 showed ratios of reaching to new fundamental value by simulation ends to 100 times simulation runs for various small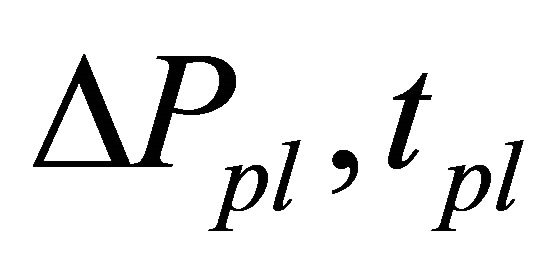 , and
, and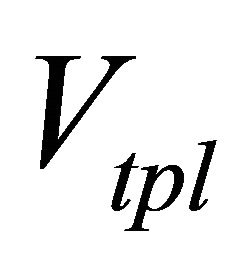 , volatilities calculated by
, volatilities calculated by 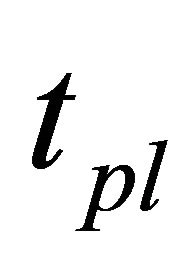 11. A shadow area satisfies an inequality constraint Equation (6),
11. A shadow area satisfies an inequality constraint Equation (6),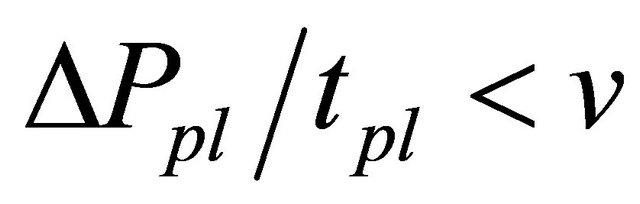 . Table 4 shows that the inequality constraint Equation (6) was not related whether or not the price converged to the new fundamental value. An upper right area above the solid line shows
. Table 4 shows that the inequality constraint Equation (6) was not related whether or not the price converged to the new fundamental value. An upper right area above the solid line shows 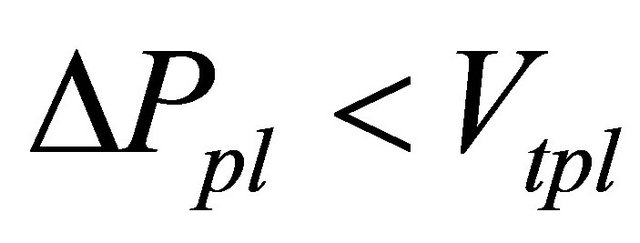 is satisfied. In this area, the market price never converged to the new fundamental value. Therefore, not only Equation (6) but also a condition,
is satisfied. In this area, the market price never converged to the new fundamental value. Therefore, not only Equation (6) but also a condition,
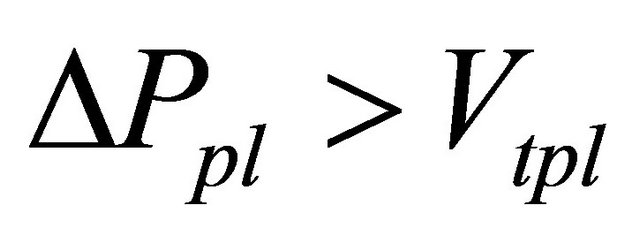 , (7)
, (7)
is needed to effective price variation limits, which make markets efficiently.
4. Conclusion and Future Study
We built an artificial market model and compared effects of price variation limits, short selling regulations and up−tick rules. In the case without the regulations, the price fell to below a fundamental value when an economic crush occurred. On the other hand, in the case with the regulations, this overshooting did not occur. However, the short selling regulation and the up-tick rule caused the trading prices to be higher than the fundamental value. We also surveyed an adequate limitation price range and an adequate limitation time span for the price variation limit and found a parameters’ condition of the price variation limit to prevent the over-shorts. We also showed the limitation price range should be bigger than a volatility calculated by the limitation time span.
One future study is to a find way to recommend actually good parameters of the price variation limit to real
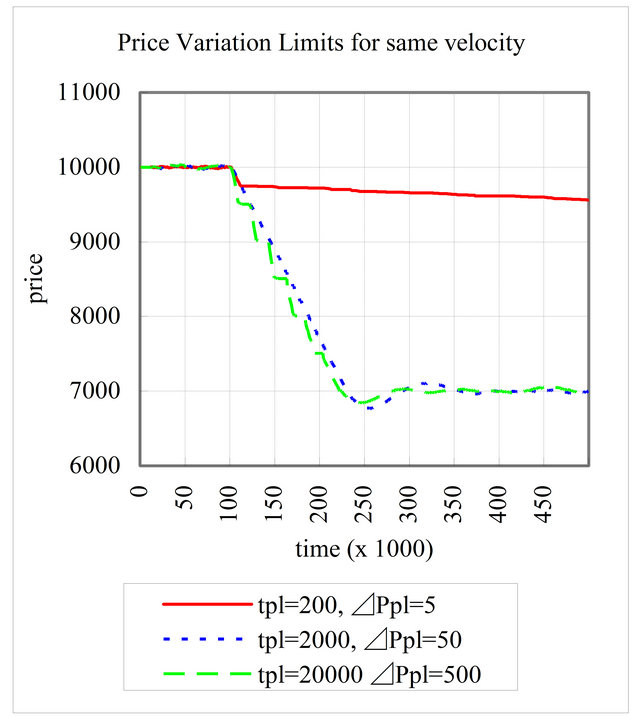
Figure 5. A time evolution of market prices in the same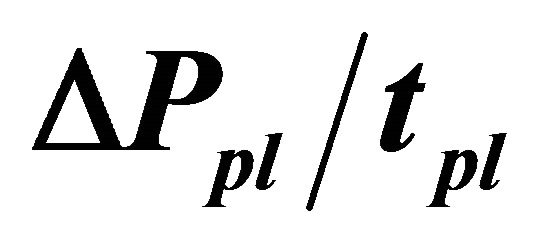 .
.
Table 4. Ratios of reaching to new fundamental value by simulation ends to 100 times simulation runs for various small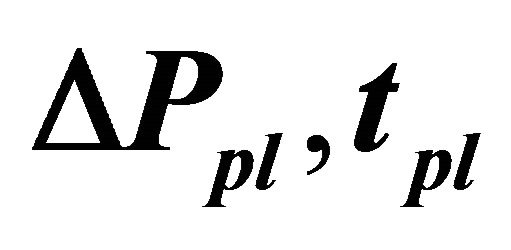 , and
, and , volatilities calculated by
, volatilities calculated by .
.
stock exchanges. We cannot observe actual  shown in section 3.4. Tokyo Stock Exchange employs two kinds of price variation limits that adopt different time spans: one is “daily price limit”, which restricts price fluctuations within a single trading day, and the other is “special quote” which restricts within three minutes [1]. We can interpret that the special quote that has a shorter time span determines
shown in section 3.4. Tokyo Stock Exchange employs two kinds of price variation limits that adopt different time spans: one is “daily price limit”, which restricts price fluctuations within a single trading day, and the other is “special quote” which restricts within three minutes [1]. We can interpret that the special quote that has a shorter time span determines 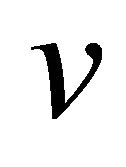 and the daily price limit that has a longer time span prevents bubbles. Thus, where parameters of the daily price limit are
and the daily price limit that has a longer time span prevents bubbles. Thus, where parameters of the daily price limit are 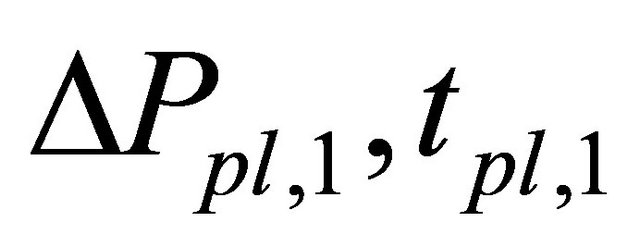 and those of the special quote are
and those of the special quote are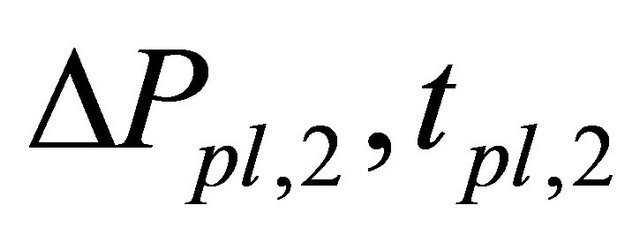 , when these parameters satisfied
, when these parameters satisfied
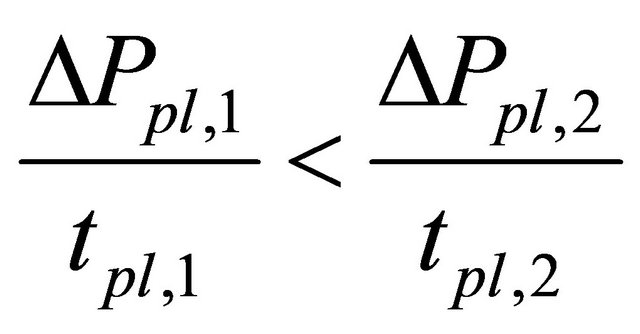 , (8)
, (8)
these price variation limits can prevent bubbles. However, the left term of Equation (8) should be not so smaller than the right term as we suggested in section 3.4. For example, 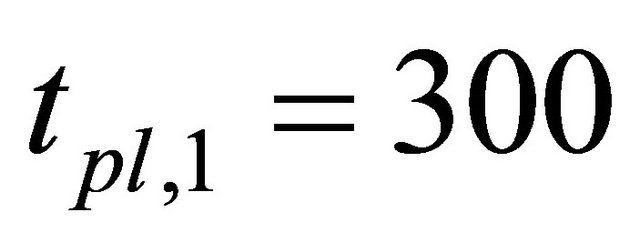 minutes,
minutes,  yen,
yen, 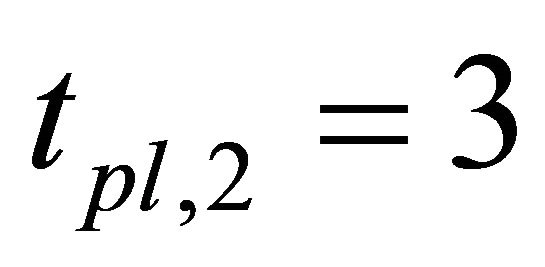 minutes, and
minutes, and 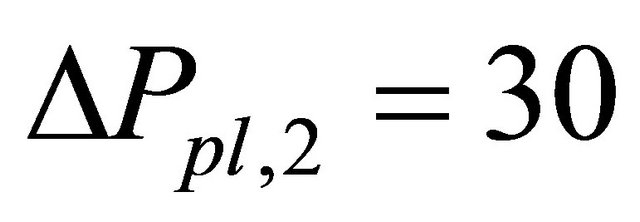 yen for stocks that have prices from 1000 yen to 1500 yen in Tokyo Stock Exchange. Therefore, Equation (8) is strongly satisfied but the left term of Equation (8) is much smaller than the right term. It is possible that the daily price limit is too tight (
yen for stocks that have prices from 1000 yen to 1500 yen in Tokyo Stock Exchange. Therefore, Equation (8) is strongly satisfied but the left term of Equation (8) is much smaller than the right term. It is possible that the daily price limit is too tight (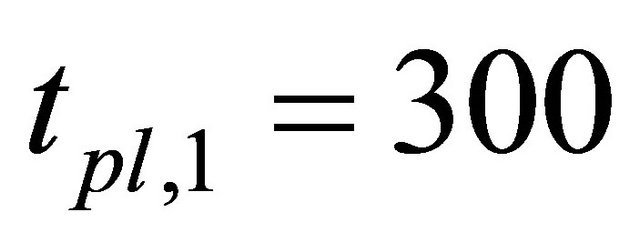 minutes is too large or
minutes is too large or 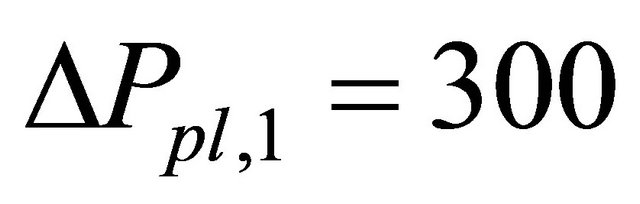 yen is too small) or the special quote is too loose (
yen is too small) or the special quote is too loose (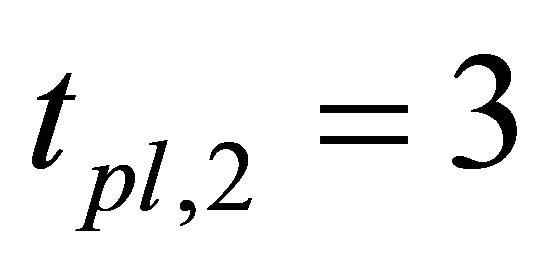 minutes is too small or
minutes is too small or  yen is too large). However, this study could not discuss such actual parameters. This is a future work.
yen is too large). However, this study could not discuss such actual parameters. This is a future work.
REFERENCES
- Tokyo Stock Exchange, “Guide to TSE Trading Methodology,” 2012.
- B. LeBaron, “Agent-Based Computational Finance,” Handbook of Computational Economics, Vol. 2, 2006, pp. 1187- 1233. doi:10.1016/S1574-0021(05)02024-1
- S.-H. Chen, C.-L. Chang and Y.-R. Du, “Agent-Based Economic Models and Econometrics,” The Knowledge Engineering Review, Vol. 27, No. 2, 2009, pp. 187-219.
- I. Yagi, T. Mizuta and K. Izumi, “A Study on the Effectiveness of Shortselling Regulation Using Artificial Markets,” Evolutionary and Institutional Economics Review, Vol. 7, No. 1, 2010, pp. 113-132.
- I. Yagi, T. Mizuta and K. Izumi, “A Study on the Market Impact of Short-Selling Regulation Using Artificial Markets,” In: Q. Bai and N. Fukuta, Eds., Advances in Practical Multi-Agent Systems, ser. Studies in Computational Intelligence, Vol. 325, Springer, Berlin, Heidelberg, 2011, pp. 217-231.
- F. Westerhoff, “The Use of Agent-Based Financial Market Models to Test the Effectiveness of Regulatory Policies,” Jahrbucher Fur Nationalokonomie Und Statistik, Vol. 228, No. 2, 2008, p. 195.
- S. Thurner, J. Farmer and J. Geanakoplos, “Leverage Causes Fat Tails and Clustered Volatility,” Quantitative Finance, Vol. 12, No. 5, 2012, pp. 695-707. doi:10.1080/14697688.2012.674301
- S. Kobayashi and T. Hashimoto, “Benefits and Limits of Circuit Breaker: Institutional Design Using Artificial Futures Market,” Evolutionary and Institutional Economics Review, Vol. 7, No. 2, 2011, pp. 355-372.
- C. Yeh and C. Yang, “Examining the Effectiveness of Price Limits in an Artificial Stock Market,” Journal of Economic Dynamics and Control, Vol. 34, No. 10, 2010, pp. 2089-2108. doi:10.1016/j.jedc.2010.05.015
- T. Mizuta, K. Izumi and S. Yoshimura, “Price Variation Limits and Financial Market Bubbles: Artificial Market Simulations with Agents’ Learning Process,” 2013 IEEE Symposium Series on Computational Intelligence for Financial Engineering Economics, Singapore City, April 2013, pp. 1-7. http://www.ntu.edu.sg/home/epnsugan/index_files/SSCI2013/index.html
- C. Chiarella, G. Iori and J. Perelló, “The Impact of Heterogeneous Trading Rules on the limit order book and Order Flows,” Journal of Economic Dynamics and Control, Vol. 33, No. 3, 2009, pp. 525-537. doi:10.1016/j.jedc.2008.08.001
- D. Friedman, “The Double Auction Market Institution: A Survey,” In: D. Friedman and J. Rust, Eds., The Double Auction Market: Institutions, Theories, and Evidence, Addison-Wesley, Boston, 1993, pp. 3-25.
- B. Mandelbrot, “The Variation of Certain Speculative Prices,” The Journal of Business, Vol. 36, No. 4, 1963, pp. 394-419. doi:10.1086/294632
- R. Cont, “Empirical Properties of Asset Returns: Stylized Facts and Statistical Issues,” Quantitative Finance, Vol. 1, 2001, pp. 223-236.
- B. Mandelbrot, “Statistical Methodology for Nonperiodic Cycles: From the Covariance to R/S Analysis,” Annals of Economic and Social Measurement, Vol. 1, No. 3, 1972, pp. 259-290.
- M. Sewell, “Characterization of Financial Time Series,” 2006.
- G. McQueen and S. Thorley, “Bubbles, Stock Returns, and Duration Dependence,” Journal of Financial and Quantitative Analysis, Vol. 29, No. 3, 1994, pp. 379-401.
- K. Chan, G. McQueen and S. Thorley, “Are There Rational Speculative Bubbles in Asian Stock Markets?” Pacific-Basin Finance Journal, Vol. 6, No. 1-2, 1998, pp. 125-151.
- I. Yagi, T. Mizuta and K. Izumi, “A Study on the Reversal Mechanism for Large Stock Price Declines Using Artificial Markets,” 2012 IEEE Conference on Computational Intelligence for Financial Engineering Economics, New York, March 2012, pp. 1-7. http://www.ieee-cifer.org/2012/index.html
- J. Frankel and K. Froot, “Chartists, Fundamentalists, and Trading in the Foreign Exchange Market,” The American Economic Review, Vol. 80, No. 2, 1990, pp. 181-185.
- R. Yamamoto and H. Hirata, “Strategy Switching in the Japanese Stock Market,” Japan Center for Economic Research Discussion Paper, No. 135, 2012.
NOTES
*It should be noted that the opinions contained herein are solely those of the authors and do not necessarily reflect those of SPARX Asset Management Co., Ltd.
1Short selling is the selling of a stock that the seller doesn’t own. Short selling regulation is that any short selling is restricted.
2Up-tick rule is that short selling except upon an up-tick of last traded price is restricted.
4A continuous double auction is an auction mechanism where multiple buyers and sellers compete to buy and sell some financial assets, respectively, in the market, and where transactions can occur at any time whenever an offer to buy and an offer to sell match [12].
5Excellent reviews are [2,3].
6This means that the kurtosis of price returns is positive. There are empirical studies for the fat-tail [13,14].
7This means that the square returns have positive autocorrelation, and the autocorrelation slowly decays as its time separation becomes larger. There are empirical studies for the volatility-clustering [14-16].
8In this model, time passes by an agent just ordering even if no dealing is done. Therefore, the returns for one tick (one time) include many zero returns, and they will bias statistical values. This is the reason we use returns for 100 time units.
9Yagi et al. showed lager amplitudes of bubbles and crushes than those of this study [4]. However, we confirmed the amplitudes were smaller and same as those of this study when initial cash was decreased.
10In the cases of the short selling regulation and the up-tick rule, the results were same as the case of the price variation.

11The volatilities were standard deviation of returns of market prices within .
.

