ABSTRACT

This paper examines optimal consumption/portfolio choices under stochastic habit formation in which it is uncertain how deep consumers would become in the habit of consuming in future. By extending Shroder and Skiadas [1] to stochastic habit formation, the optimization problem with stochastic habit forming preferences is transformed into that with simple time-additive preferences. Optimal portfolios are composed of the tangency portfolio and habit hedging portfolio. Resulting risk premia are characterized by consumption beta, which is proportionate to the covariance with consumption changes, and habit beta, defined by using the covariance with habit.

1. Introduction

Habit formation has been reported in the literature to play important roles in individual consumers’ intertemporal decisions and macroeconomic phenomena [2,3]. One of the seminal papers by Sundaresan [4] shows that adjacent complementarity in consumption due to habits lowers the intertemporal elasticity of substitution and, consistently with the empirical fact [5], thereby making consumption less volatile. Constantinides [6] derives implications of this effect on the equity premium puzzle.1 The restricted assumption that has been put commonly in the existing literature is that the process of habit formation is deterministic so that consumers can predict perfectly their future habits once their plans of the future consumption stream are set. In reality, however, even with a given consumption stream, it is quite uncertain how deep consumers would become in the habit of consuming in future. The resulting consumers’ choices and hence asset price dynamics would be affected by the risk associate with habit formation.

By extending the habit model by incorporating uncertainty over the habit formation process, the purpose of this paper is to explore the implications of the habit shifting risk for optimal consumption/portfolio choices and for asset pricing.2 As my main conclusions, it is shown that 1) by extending [1], the optimization problem with stochastic habit forming preferences can be transformed into that with simple time-additive preferences; that 2) consumers’ optimal portfolios are composed of tangency portfolio, which has minimum variance of returns, and habit hedging portfolio, duplicating stochastic habit formation; and that 3) risk premia of asset returns are characterized by consumption beta, which is proportionate to the covariance with consumption changes, and habit beta, defined by using the covariance with fluctuations in the habitual subsistence level.

The key relation underlying these results is the optimal condition that the marginal utility of wealth equals that of contemporaneous utility of consumption plus the shadow price of the uncertain future habit stream.

As in [6], the optimal surplus consumption, defined as consumption in excess of subsistence level, is expressed as proportionate to surplus wealth defined as wealth in excess of the capitalized value of future uncertain habitual subsistence level (say, the habitual subsistence wealth). A distinct feature in my paper is that the marginal propensity to consume and habitual subsistence wealth both depend on risk associate with habit formation.

The optimal portfolios are composed of riskless bond, the tangency portfolio and habit hedging portfolio, that is, three-fund separation holds. Wealth is divided into two parts; surplus wealth and habitual subsistence wealth. The amount of habitual subsistence wealth is invested in habit hedging portfolio and riskless bond to finance future uncertain habitual subsistence level. While, the residual wealth: surplus wealth is invested in tangency portfolio and riskless bond to finance surplus consumption.

From the optimal condition, stochastic movement of the marginal utility of wealth is duplicated by fluctuations in consumption and that in habitual subsistence level. As a result, risk premia are characterized by consumption beta and habit beta. One important implication of this for the risk premium puzzle is that neglecting the effect of the habit beta might lead to underestimation of the risk underlying security returns, and hence to overestimation of risk aversion parameters.

By using an endowment economy model with deterministic habit formation, Detemple and Zapatero [10] derive a two-factor pricing formula with consumption beta and habit beta which is perfectly correlated to changes in shadow price of habit.3 However, in the deterministic opportunity set, shadow price of habit is perfeclty correlated to changes of consumption and it turns to be single consumption beta model. In contrast, by assuming a constant opportunity set, we show that the stochastic habit formation preference results in a two-factor model with habit and consumption betas.

The remainder of this paper proceeds as follows. The model is presented in Section 2. Section 3 provides the optimal solution under linear stochastic habit formation by applying the linear transformation procedure developed by [1]. Section 4 characterizes risk premia and riskfree interest rates. Section 5 concludes the paper.

2. The Model

Suppose that a representative consumer endowed with an initial wealth W(0) faces D + 1 investment opportunities: one riskless bond and D risky assets. Underlying the model is a complete probability space 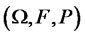where Ω is the set of states of nature, F is the σ-field of events, and P is a probability measure on. A D-dimensional standard Wiener process B is defined on.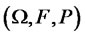

The riskless bond yields a constant rate of return, r. The price of i-th risky asset (i = 1, ···, D) is given by

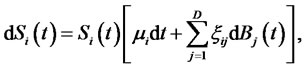(1)

where 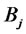(j = 1, ···, D) are independent of each other:

4This specification of habit dynamics is no longer valid in incomplete market economy because consumption surplus can be negative with positive probabilities.

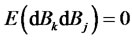if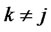; and expected returns and diffusion coefficients 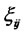are assumed to be constant. I assume that the markets are complete in which 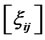has full rank D. The market-price-of-risk process η i.e., risk premium on portfolios that duplicate is thus determined uniquely as follows,

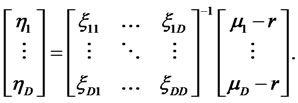
The representative consumer determines the optimal portfolio and consumption processes in order to maximize his expected lifetime utility specified as follows,

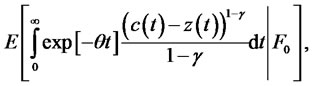(2)

where is subjective discount rate; is a parameter related with relative risk aversion; c and z are consumption and habitual living standard, respectively.

The key assumption in this paper is that the habitual living standard grows stochastically as follows,

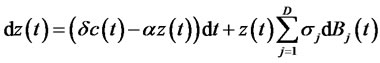, (3)

or integral representation

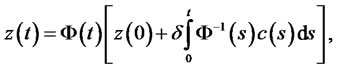(4)

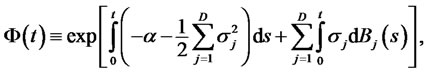
where the parameters and 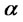measure intensity of consumption and the depreciation rate of the past habit, respectively. In (3) or (4), his habitual living standard depends not only on his past consumption history but also on states of nature. From the assumption of complete markets, the habit shifting shocks are given by the same Brownian motions as in (1). The stochastic property of the shocks is thus captured by diffusion term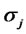.4

3. Optimal Consumers Behavior with Stochastic Habit Formation

With an initial wealth W(0) and an initial habitual living standard z(0), the representative consumer determines the optimal policies for consumption c and proportion 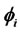of risky asset portfolio subject to the following dynamic budget constraint,

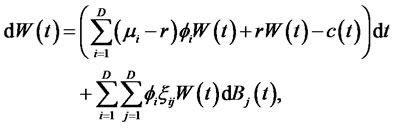(5)

and the habit formation process (3).

Thus, the optimization problem is summarized as

(6)

subject to (3) and (5).

3.1. Subsistence Wealth

To solve the problem, I first obtain the capitalized value of habit to finance the future uncertain habitual living standard, I refer it the value as the habitual subsistence wealth. Following [10], consider the “subsistence policy” in which consumption level at each instant is set equal to contemporary habitual living standard; c(s) = z(s), s > t. From (3) and the definition, the subsistence policy is obtained as

Letting H(t) be state price deflator as

(7)

the habitual subsistence wealth level is obtained by capitalizing the subsistence consumption stream with H as

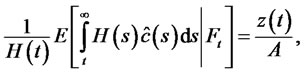
where

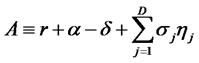, (8)

which represents the rate of return on the habitual subsistence wealth. I impose a restriction A > 0 for convergence.

Unlike in the case of deterministic habit formation [6]the discount rate A includes risk premium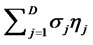which, from (3) and (7), equals the risk of habit formation, measured by the covariance per unit of time with the state price deflator. Note that the term can be either positive or negative, depending on the underlying the risk price structure and the diffusion coefficients of habit formation σ. Furthermore, from the assumption of complete markets, the subsistence wealth is derived by simple arbitrage pricing theory.

3.2. Transformation

Due to linear structure of habit formation, I can follow [1] in transforming the optimization problem (6) into that with simple time-additive preferences.

Define surplus wealth and surplus consumption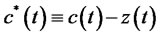. Two stochastic differential equations (3) and (5) can be combined into single equation with respect to surplus wealth deflated by H(t),

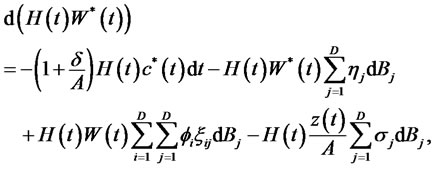
which can be integrated as

(9)

This lifetime budget constraint requires that the present value of the surplus consumption stream equals the initial value of surplus wealth, where surplus consumption at each instant is evaluated by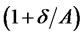. A surplus consumption 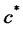deepens the future habit stocks by rate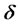, which in turn increases the required value of the subsistence wealth and thereby decreases available surplus wealth. 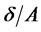represents these additional costs of surplus consumption. To ensure the existence of optimal policies, I impose the restriction on the initial condition that.

Using surplus consumption and surplus wealth, the optimization problem (6) is reduced to that with simple time-additive preferences.

Proposition 1. The optimization problem for a consumer facing risk over habit formation process reduces to that for a consumer with time-additive preference over surplus consumption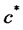 and with single lifetime budget constraint (9) as follows,

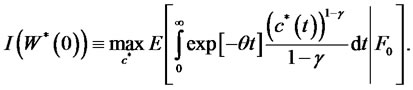(10)

3.3. Optimal Consumption and Investment Rules

Letting y be the present value of Lagrange multiplier associated with the lifetime budget constraint (9), the necessary condition for optimality is

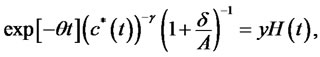(11)

which requires that the marginal utility of consumption be equal to the marginal utility of wealth. Note that due to linear structure of habit formation, shadow price of habit can be represented by contemporaneous marginal utility.

The optimal policy for surplus consumption can be obtained by substituting solutions y and H(t) into this condition. The Lagrange multiplier y can be obtained by substituting (11) into (9),

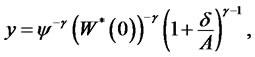(12)

where 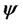is given by

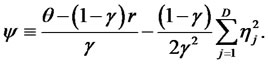
Substituting (12) into the first order condition (11) gives optimal surplus consumption process

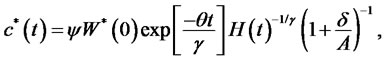(13)

From (9), surplus wealth is given as follows,

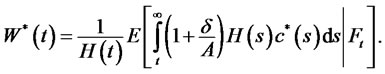(14)

Substituting (13) into (14) gives optimal surplus wealth process

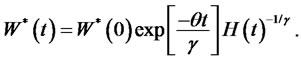(15)

Substituting (15) into (13) provides optimal consumption process as follows,

, (16)

or

. (17)

Applying Ito lemma to (15) gives

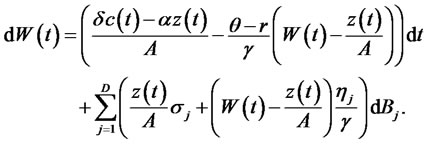(18)

As shown in Karatzas and Shreve [12], since optimal portfolio is constructed to duplicate this wealth process (18), the diffusions term of (18) must be the same as that of (5):

This relation provides optimal portfolio as follows,

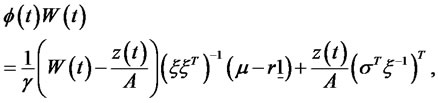(19)

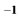where and denote transpose and inverse, respectively; and 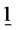denotes the D-dimensional vector with each component equal to one. Finally, substituting (16) into (10) provides the value function as follows,

As in the literature [6,13], (16) implies that the optimal surplus consumption is determined as the value of surplus wealth multiplied by the marginal propensity to consume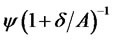. A unique property of the present model is that the discount rate and hence the marginal propensity to consume 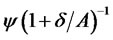depend on the degree of riskiness of habit formation.

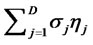Wealth W(t) is composed of surplus wealth W(t)-z(t)/A and subsistence wealth z(t)/A. As for the surplus wealth, the usual two-fund separation theorem holds, so that it is held in the form of the tangency portfolio and the riskless bond. The subsistence wealth is held in the form of the habit hedging portfolio that duplicates random parts of habit formation and the riskless bond that is used to duplicate the drift part.

Note that in the case of deterministic habit formation [13], the subsistence consumption process can be duplicated by holding the riskless bond and the two-fund separation theorem holds. In contrast, with stochastic habit formation, the habit hedging portfolios as well as the riskless bond are needed to duplicate the subsistence consumption process. As a result, a three-fund separation holds.⁵

4. Asset Pricing Implications

Previous section derives optimal consumption and portfolio rules in the production economy where risk-free rate is constant and risky production technologies follow (1). This section characterizes risk premium and risk-free interest rate to make sure of the relationship between consumption and asset pricing.

As discussed in (11), due to linear structure of habit formation, the present model can duplicate the shadow price of habit by contemporaneous marginal utility. Applying Ito lemma to (11) yields

Dividing both sides by (11) yields

Equating both sides of the deterministic and stochastic parts provides as follows,

(20)

(21)

where 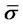and 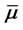are diffusion coefficient and expected rate of surplus consumption growth, respectively.

From the definition of, (20) reduces to

(22)

where 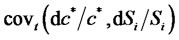is instantaneous covariance of surplus consumption growth rate with i-th stock return.6 Substituting 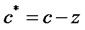into (22) provides two-factor asset pricing formula as follows,⁷

Proposition 2. Risk premium is characterized by two factors: consumption beta and habit beta

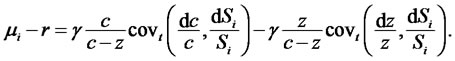
Note that risk premium is give by weighted average of covariance of consumption and that of habitual living standard. This implies that economic risks over the assets are captured not only by consumption risk but also habit risk.8 In the case that risky assets are negatively correlated to habit, observers who lack evaluating risk over habit tend to underestimate risk premium.

By using definitions of and, (21) reduces to

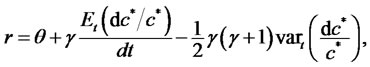(23)

where is instantaneous variance of surplus consumption growth rate.

9In the case of time-additive utility, Gollier [17] provides three basic determinants: the pure time preference for the present, consumption smoothing effect, and the precautionary effect.

Substituting 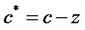into (23) provides risk-free interest rate as follows:

Proposition 3. Risk-free interest rate is characterized by

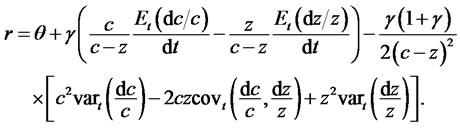
This implies that the risk-free interest rate is characterized by 6 determinants.9 The second and third terms correspond to surplus consumption smoothing effect. The second term is positive because the growth rate of consumption induces the present consumption thereby requiring a higher return on the saving. The third term is negative because the high growth rate of habitual living standard induces the reserve thereby increasing the investment in risk-free asset.

Last three terms capture the precautionary effect caused by the risk over surplus consumption. Provided that the consumer is prudent, volatilities of consumption and habit are negatively correlated to the risk-free interest rate.

5. Conclusions

This paper examines optimal consumption/portfolio choices under stochastic habit formation. Due to introducing surplus consumption and single lifetime budget constraint with respect to surplus wealth, this optimization problem with stochastic habit forming preferences is transformed into that with simple time-additive preferences.

Asset pricing implications are provided as follows. From the optimal condition that the marginal utility of wealth equal that of contemporaneous utility of consumption plus the shadow price of habit, the marginal utility of wealth is driven by the fluctuations in the habitual subsistence level and those in the consumption. Therefore, for stochastic habit forming consumers, risks are measured both by covariance with changes in consumption and by covariance with fluctuations in the habitual subsistence level. One empirical implication of this is that provided that risky assets are negatively correlated to habit, observers who lack evaluating risk over habit tend to overestimate risk aversion parameters.

6. Acknowledgements

The author is grateful to Shinsuke Ikeda for encouragement and valuable comments. I would like to thank Yuichi Fukuta, Kazuhiko Hashimoto, Keichi Hori, Yoshiyasu Ono, Akiko Yamane and the participants at the annual meeting of Japanese Economic Association at Osaka Gakuin University.

REFERENCES

NOTES

¹Ikeda [7] provides excellent survey of habit formation about macro economics and asset pricing implications.

²Dai [8] provides similar stochastic habit formation in general equilibrium model to explain the dynamics of risk-free interest rate. In contrast, the present paper provides closed form solutions for the consumption/portfolio problems and simple asset pricing formulas at the cost of assuming constant investment opportunity set. Dai and Grishchenko [9], using labor income as proxy for stochastic habit, report that stochastic internal habit formation models provide better explanation of time-variation in expected returns compared to other models.

³In general, with habit forming preference, shadow price of habit at time t depends on all future consumption stream after time t. Therefore the stochastic movement of shadow price of habit is no longer duplicated by contemporaneous consumption. Instead, it can be duplicated by all future consumption stream. Therefore, as Bergman [11] shows, single consumption beta model is no longer valid.

⁵Svenson and Werner [14] obtain similar results in the presence of nontraded assets. They show that agents with non-traded assets determine optimal investment and consumption rules subject to budget constraint that consists of financial wealth plus implied value of their non-traded assets. Uncertainty over non-traded assets affects their decisions only through the implied value of non-traded assets thereby not affecting the marginal propensity to consume. In contrast, uncertainty over the habit formation affects not only the capitalized value of habit but also the costs of consumption thereby affecting both the level of consumption and the marginal propensity to consume.

⁶Chapman [15] obtains similar pricing formula with deterministic habit formation by putting a restrictive assumption that surplus consumption follows Geometric Brownian motion. Instead of such restrictive assumption, the present model reduces to (22) with specific risky technology as in (1).

⁷Bakshi and Chen [16] provide a similar formula in an economy populated with capitalistic investors.

⁸Due to the specific technologies as in (1), marginal utility of consumption is represented by contemporaneous marginal utility multiplied by constant parameter. As a result, marginal utility of wealth can be duplicated by contemporaneous consumption and habit, and then two-factor model is obtained. In general, it is replaced by three-factor model since multiplier also shifts.