Open Journal of Ecology
Vol.07 No.01(2017), Article ID:73565,7 pages
10.4236/oje.2017.71003
Statistical Transformation Indicators of Short-Term to Long-Term Using Flood Regional Coefficients (Case Study: East Azarbaijan Province, Iran)
Iraj Ebn Abbas1, Maaroof Siosemarde2*
1Department of Civil Engineering, Mahabad Branch, Islamic Azad University, Mahabad, Iran
2Department of Water Engineering, Mahabad Branch, Islamic Azad University, Mahabad, Iran

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 4, 2016; Accepted: January 15, 2017; Published: January 18, 2017
ABSTRACT
Changing contexts in a long-term and short-term perspective should be managed within an integrated risk management framework that accounts for both temporary management strategies and permanent preventive measures to reduce the impact of natural hazard processes. In this study, statistical transformation indicators of short-term (20 year) to long-term (30 year) used flood regional coefficients. After the tests of data validation and the reconstruction of missing and outlier data, the data of 18 hydrometric stations were completed for 30 years (1985 to 2014). In the next phase, the return period values were prepared for 20-year and 30-year statistical periods (1985 to 2004 and 1985 to 2014) using the HYFA software. Thus the 20-year to 30-year ratio for various return period discharges obtained and these dimensionless values were plotted for the return periods of 2, 5, 10, 20, 50 and 100 years, also fitted the logarithmic trend line and the values of coefficients of the relationship were obtained. The statistics including average, standard deviation, coefficient of variation (CV), skewness coefficient (CS) and Kurtosis coefficient (CK) were calculated for 20-year data period for each station and we identified the statistics as independent parameters and the coefficients of A and B as dependent parameter, thus analyzed using linear multivariate regression, and regional factors were obtained. In the hydrometric station with 17-027 code, the discharge using the regional factors was calculated and compared with the discharge values of 30 years data. The results showed that there is little difference between the observed and estimated values from regional factors thus this method can be used in projects that require at least 30 years of data.
Keywords:
Factor Analysis, Flood, Long-Term, Short-Term, Regional Factors

1. Introduction
Flood frequency curves describe the relationship between the magnitude of river peak flows and the recurrence interval or return period. They can be derived from data at flow monitoring stations and regionalized for use at any location along the basin’s river network, by relating the spatial differences to geographical regions and to variations in upstream sub-basin characteristics inside each region. Regional flood frequency analysis is used for the estimation of floods at sites where little or no data are available. It involves the identification of groups (or regions) of hydrologically homogeneous catchments and the application of a regional estimation method in the identified homogeneous region.
According to global and European reports [1] [2] , in past decades the number of disasters caused by natural hazards has demonstrated an increasing trend fueled by changing contexts in socioeconomic, environmental and climatic patterns.
There are three commonly-used methods for handling for consistency of hydrological series, i.e. genetic analysis method, discard method, and direct calculation method. The genetic analysis method has a clear target, so the method has been widely used for handling hydrological consistency. When the discard method is being used, it should have a sufficient time-series length, so this method has limitations. The direct calculation method is a method for which the theoretical derivation and actual application have been conducted by Xia et al. (2005) [3] . It is strongly theoretical but has relatively high uncertainty.
In the design of water conservancy projects, the calculation of design flood is undoubtedly a key step. Frequency analyses are needed. The reliability of the result is related to the reliability, consistency and representativeness of the hydrological series employed. Hydrological series are influenced by many factors and the influence of human activities is comparatively prominent [4] .
According to Tasker and Stedinger (1987) [5] , useful flood information can be obtained for the pregauged period by incorporating paleoflood data, and, in so doing, to supplement the systematic gauge record at a site. Palaeoflood hydrology is a reconstruction of the magnitude and frequency of recent, past, and ancient floods (approximately 50, 500 and 5000 years ago, respectively) using geological evidence [6] .
2. Methodology
East Azerbaijan Province is one of the 31 provinces of Iran. It is located in north west of Iran, bordering with Armenia, Republic of Azerbaijan, Ardabil Province, West Azerbaijan Province and Zanjan Province. The capital of East Azerbaijan is Tabriz. The province covers an area of approximately 45,481 km2, it has a population of around four million people. The highest peak of East Azerbaijan is Sahand Mountain at 3722 m of elevation, lying south of Tabriz, whereas the lower lying areas are around Garmadooz (Ahar). In hydrology at least 30-year period has been recommended to approach the statistical population. The main problem in many regions, especially East Azerbaijan province is short of time during of data in hydrometric stations. Therefore, use of short-term data is needed to estimate the flood with long return period.
In this study carried out the outlier test and the result showed that the outlier data there are in 8 hydrometric stations. Thus correlation matrix obtained for 18 hydrometric stations. Thus missing and outlier data reconstruction based on regression relationship. The data of 18 hydrometric stations were completed for 30 year (1985 to 2014).
3. Results
In this study, the return period values were prepared for 20-year and 30-year statistical periods (1985 to 2004 and 1985 to 2014) using the HYFA software. The three-parameter log Pearson distribution was recognized as the dominant distribution and the values of discharge calculated for return periods of 2, 5, 10, 20, 50 and 100 years based on 20-year and 30-year period using the HYFA software are shown in Table 1.
Thus the 20-year to 30-year ratio for various return period discharges obtained and these dimensionless values are plotted for the return periods of 2, 5, 10, 20, 50 and 100 years that Figure 1 and Figure 2 showed the regression relationship between (Q20/Q30) * 100 and return period in hydrometric stations code of 17-027 and 19-067 as sample.
A logarithmic equation fits the data; the equation for the logarithmic relationship is (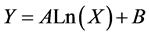 ) where Y is
) where Y is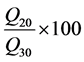 , X is return period (year), A and B are the values of coefficients of regression relationship that showed in Table 2.
, X is return period (year), A and B are the values of coefficients of regression relationship that showed in Table 2.
The statistics including average (AV), standard deviation (SD), coefficient of variation (CV), skewness coefficient (CS) and Kurtosis coefficient (CK) were calculated for 20-year data period for each station and we identified the statistics as independent parameters and the coefficients of A and B as dependent parameter, thus analyzed using linear multivariate regression, and regional factors were obtained that showed following:
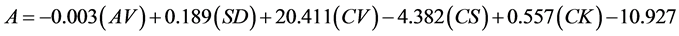 (1)
(1)
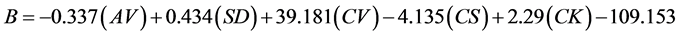 (2)
(2)
The various statistics were calculated for 20-year data period for each station and the coefficients of A and B were shown in Table 3.
Therefore the Q30 discharge data for various return periods (X) were calculated using following relationship:
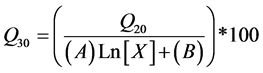 (3)
(3)
In the hydrometric station of 17-027 code, the discharge using the regional factor was calculated and compared with the discharge values of 30 years data that showed in Table 4.
The results showed that the statistics of R, RMSE, MAE and RE were obtained
Table 1. The values of discharge calculated for return periods of 2, 5, 10, 20, 50 and 100 years based on 20-year and 30-year period using the HYFA software.
Figure 1. The regression relationship between (Q20/Q30) * 100 and return period in hydrometric stations code of 17-027.
Figure 2. The regression relationship between (Q20/Q30) * 100 and return period in hydrometric stations code of 19-067.
Table 2. Values of coefficients of regression relationship.
Table 3. The various statistics were calculated for 20-year data period and the coefficients of A and B.
Table 4. The values of calculated discharge using regional factor and observation discharge of 30 years data in hydrometric station of 17-027 code.
as 0.9998, 3.80, 3.47 and 4.38 respectively. The results showed that there is little difference between the observed and estimated values from regional factors thus this method can be used in projects that require at least 30 years of data.
Cite this paper
Abbas, I.E. and Siosemarde, M. (2017) Statistical Transformation Indicators of Short-Term to Long- Term Using Flood Regional Coefficients (Case Study: East Azarbaijan Province, Iran). Open Journal of Ecology, 7, 34-40. http://dx.doi.org/10.4236/oje.2017.71003
References
- 1. EEA (European Environment Agency) (2010) Mapping the Impacts of Natural Hazards and Technological Accidents in Europe—An Overview of the Last Decade. EEA Technical Report No. 13/2010, Copenhagen.
- 2. UNISDR (United Nations International Strategy for Disaster Reduction) (2011) Global Assessment Report on Disaster Risk Reduction: Revealing Risk, Redefining Development, United Nations International Strategy for Disaster Reduction. Open File Rep., Geneva, 178 p.
- 3. Xie, P., Chen, G.C. and Xia, J. (2005) Hydrological Frequency Calculation Principle of Inconsistent Annual Runoff Series in Changing Environments. Journal of Wuhan University, 38, 6-9.
- 4. Liang, Z.M., Hu, Y.M. and Wang, J. (2011) Advance in Study on Hydrological Frequency Analysis of Inconsistency. Advances in Water Science, 22, 864-871.
- 5. Tasker, G.D. and Steninger, J.R. (1987) Regional Regression of Flood Characteristics Employing Historical Information. Journal of Hydrology, 96, 255-264.
https://doi.org/10.1016/0022-1694(87)90157-0 - 6. Baker, V.R., Webb, R.H. and House, P.K. (2002) The Scientific and Societal Value of Paleoflood Hydrology. In: House, P.K., Webb, R.H., Baker, V.R. and Levish, D.R., Eds., Ancient Floods, Modern Hazards: Principles and Applications of Paleoflood Hydrology, Water Science and Application Series Vol. 5, American Geo-physical Union, Washington DC, 127-146.




