Received 13 January 2015; accepted 27 March 2015; published 2 April 2015

ABSTRACT

Prominent examples of predator-prey oscillations between prey-specific predators exist, but long- term data sets showing these oscillations are uncommon. We explored various models to describe the oscillating behavior of coyote (Canis latrans) and black-tailed jackrabbits (Lepus californicus) abundances in a sagebrush-steppe community in Curlew Valley, UT over a 31-year period between 1962 and 1993. We tested both continuous and discrete models which accounted for a variety of mechanisms to discriminate the most important factors affecting the time series. Both species displayed cycles in abundance with three distinct peaks at ten-year intervals. The coupled oscillations appear greater in the mid-seventies and a permanent increase in the coyote density seems apparent. Several factors could have influenced this predator-prey system including seasonality, predator satiation, density dependence, social structure among coyotes, and a change in the coyote bounty that took place during the course of data collection. Maximum likelihood estimation was used to obtain parameter values for the models, and Akaike Information Criterion (AIC) values were used to compare models. Coyote social structure and limiting resources in the form of density-dependence and satiation seemed to be important factors affecting population dynamics.

Keywords:

Coyotes, Jackrabbits, Oscillations, Predator-Prey Cycles, Model Competition

1. Introduction

Predator-prey interactions among a wide variety of organisms have been studied extensively under various ecological conditions. Studies show that the abundance of prey-specific predators (those which prey upon a single species almost exclusively) is subject to fluctuations dependent on the abundance of the prey species. The most prominent example of such patterns existing in mammalian species is between the lynx (Lynx canadensis) and snowshoe hare (Lepus americanus) using nearly a century’s worth of pelt records from the Hudson Bay Company. These data produced cycles with peak abundance every ten years for both species [1] . Other long-term data sets are rare, and most lab experiments quickly result in the extinction of one or both species [2] . It is also difficult to obtain sufficient lab or field data depicting such oscillatory patterns, especially in vertebrates, since resources are limited and long-term studies can be very expensive.

A well-known example of these trade-offs occurs between the protist ciliate species Paramecium aurelia and Didinium nasutum [3] . Luckinbill was able to produce such patterns with P. aurelia and its predator, D. nasutum, in a homogenous lab environment using methyl cellulose to inhibit the frequency of predator-prey interaction. Previous attempts at producing oscillatory data in a lab environment required the addition of new organisms, mimicking dispersal, or by adding physical complexity to the system which allowed the prey species to find refuge from predation. This type of manipulation simulates a natural heterogeneous environment where prey are able to hide from predators, and are prevented from unlimited growth by natural constraints. Luckinbill was able to create oscillatory data only by limiting the frequency of contact between species, as well as manipulating the food supply for Paramecium. His results suggest that limitations on both the prey’s food availability, as well as the predator’s capture rate, are important factors influencing the existence of coupled oscillations of abundance.

Many mathematical models have been developed to explain this kind of relationship between predators and prey, beginning with Lotka (1925) and Volterra and Brelot (1931) [4] [5] . Their model(s) included a growth rate for the predator depending linearly on prey density and a commensurate death rate for the prey. However, prey conversion into new predators in this model is instantaneous, and the prey species has unrestricted growth. Roszenweig and MacArthur (1963) and Beverton and Holt (1957) later refined these types of models to include resource limitations for one or both species [6] [7] . Saturable predation responses (e.g., the type II functional response described by Holling, 1959) were included so that the frequency of prey consumption was intrinsically limited [8] . Limitations on the growth of the prey species were also included in these models in the form of “carrying capacity,” the number of individuals a certain area can support. Today, it is widely accepted that both density dependence and saturable predation are essential components of predator-prey models.

Harrison (1995) was able to successfully model Luckinbill’s Paramecium and Didinium data by incorporating type II predation and carrying capacity, in addition to a delayed numerical predator response in standardized predator-prey models [9] . Harrison fit several different models to the data, and compared results using summed square error. He also introduced a time-lag in the rate of prey conversion, and this delayed numerical response with saturable predation proved to best fit Luckinbill’s data.

Another study conducted by Dennis et al. (1995) modeled the cannibalistic population interactions of the flour beetle, Tribolium castaneum, using a system of nonlinear difference equations [10] . Notably, a time-series approach using maximum likelihood and conditional least squares estimation was used to determine model parameters. Their experiment included several populations which were subject to identical lab conditions with model coefficients estimated individually for each population. Their analysis failed to reject the hypothesis that all populations had the same parameter values, supporting the use of these methods as an effective way to obtain model coefficients.

Knowlton and Stoddart (1992) modeled a 31-year data set of coyote (Canis latrans) and black-tailed jackrabbit (Lepus californicus) abundances in Curlew Valley, Utah using a seasonal time-step approach [11] . Four equations were developed and parameterized individually representing 1) coyote population change, 2) jackrabbit natality, 3) adult jackrabbit mortality, and 4) juvenile jackrabbit mortality. They were able to successfully reproduce cyclical patterns of abundance in the system, but included two ad hoc constraints (not allowing the jackrabbits to fall below very low levels of abundance, simulating availability of refuges or emigration into the area and placing an upper limit on coyote abundance). Their model reproduced the three distinct cycles evident in the data and results from the study supported the notion that jackrabbits are a majority prey-item for coyotes.

In another study conducted by Bartel and Knowlton (2005), coyotes demonstrated non-trivial functional feed- ing responses in reaction to varying levels of prey abundance [12] . Specifically, coyotes displayed a hyperbolic (type II) feeding response characterized by increasing predation for increasing prey abundance before the relationship asymptotically levels off. Thus, predator satiation is likely to be a factor in this predator-prey system. Pitt et al. (2003) developed an individual-based computer model to test the effects of coyote social structure on population dynamics [13] . This model distinguished between transient coyotes and territorial coyotes since transient coyotes are likely to have higher mortality rates. Social dynamics could affect the success rate of prey capture and handling times because pack coyotes collaborate to take down larger prey. Only territorially dominant females were allowed to reproduce in the simulation. However, this model assumed a homogeneous food supply, unlikely in a natural environment. Still, results suggested that territoriality and social structure limited reproduction, which could influence predator-prey dynamics.

Multiple models have been developed to describe predator-prey relationships, but rarely have individual influencing factors been assessed using competing models on the same system. Here we used several predator- prey models to describe Knowlton’s unique data set to discriminate which mechanisms have the greatest effect on abundance, testing effects of satiable predation, density dependence and consequences of social hierarchy at the population level. Continuous and discrete models were examined to evaluate the effects of seasonality and changing anthropogenic influences (e.g., changes in coyote bounties) on the populations. Parameter estimates were obtained using nonlinear maximum likelihood estimation (MLE), and models were compared using the Akaike Information Criterion (AIC).

2. Methods

2.1. Site Description and Data Collection

Curlew Valley is located in Box Elder County in northeastern Utah on the border of Idaho. This area is dominated by big sagebrush (Artemisia tridentata), rabbitbrush (Chrysothamnus nauseousus or C. viscidiflorus), greasewood (Sarcobatus vermiculatus), as well as agricultural crops including crested wheatgrass (Agropyron cristatum) and alfalfa (Medicago sativa) [14] . Curlew Valley is mainly managed by the Bureau of Land Management, and thus seasonal grazing by cattle and sheep occurs on much of the valley [12] . Elevation is approximately 1280 m on the southern edge of the valley floor and gradually rises to the north by about 5.7 m/km [14] . Many small mammals inhabit the area including the deer mouse (Peromyscus maniculatus), the Great Basin pocket mouse (Perognathus parvus), Ord’s Kangaroo rat (Dipodomys ordi) and the least chipmunk (Tamias minimus) in addition to several lagamorph species with the black-tailed jackrabbit being the most prevalent. The coyote is the primary predator in this area, preying extensively on black-tailed jackrabbits. However, there has been some evidence of prey-switching to rodents and voles when jackrabbit numbers are low [12] . Other carnivores are also present in the area, including the striped skunk (Mephitis mephatis), weasel (Mustela frenata), and an occasional cougar (Puma concolor).

Both coyotes and jackrabbits are considered pest species in Utah, so hunting is unrestricted all year round [15] [16] . Harvest rates, the number of animals “taken” by humans, varied during the course of our data set for both species. Utah offers bounties for coyotes, which have ranged from $8 to $50 per pelt over the past thirty five years. In particular, the bounty decreased by almost half in 1988 and remained low until 1992 [17] . Moreover, coyotes are part of Utah’s predator management plan so the state’s Division of Wildlife Resources (DWR) oversees additional removal of coyotes in target areas. Usually management is directly associated with livestock predation or used to alleviate the effects of coyotes on local mule deer herds [15] . Alternatively, white and black- tailed jackrabbits are not regulated by the state and, according to the Utah DWR, can be “hunted any time with any weapon” [16] . Lack of regulation has led to questionable eradication practices for both species including the use of poisons (e.g., 1080, sodium monoflouroacetate) on coyotes, spotlighting, and the historic round-ups and clubbing of jackrabbits in nearby southern Idaho [18] . These management practices may have affected the prevalence of both species in this study, but the effect is hard to quantify since Utah does not require hunters to report the taking of pest species. However, we can assume that this hunting pressure remained relatively constant throughout the study period.

Abundance indices were measured for jackrabbits using flushing transects each spring and fall between fall of 1962 and spring of 1993 in a 640 square kilometer portion of the valley. Data for jackrabbits were complete with the exception of the spring measurements in 1987 and 1988. Coyote indices were estimated by catch-per-unit efforts, scent station visitation, and scat deposition rates. Fall coyote observations were complete from 1963 to 1992. However, spring coyote measurements were only taken from 1974-1986, and from 1989-1992. These values were then normalized and averaged for a single density index value for coyotes each season [11] . Although data for both species were only indices, not actual population counts, we treated them as surrogates for actual abundance and state “jackrabbit abundance” or “coyote abundance” in place of “observed jackrabbit index” or “observed coyote index.” Therefore parameter estimates will reflect index values instead of population num- bers. Jackrabbit abundance peaked in 1970, 1980, and 1990 with peaks in coyote abundance occurring shortly after in 1972, 1983, and again in 1987 (Figure 1). However, coyote abundance deviated from this oscillating pattern since values were noticeably higher after 1980.

2.2. Mathematical Models for Coupled Population Dynamics

2.2.1. Continuous Models

These models assume continuous rates of reproduction and mortality, independent of season since abundance indices are updated constantly. Thus, the effects of a birthing season or harsh winter mortality, for example, are not included; rather, such responses are integrated with decreasing weight over all past population states.

The Lotka-Volterra model was used as the “null” model to test out our hypotheses concerning the various factors influencing the dynamics of this system. This model assumes exponential growth of the prey species, not limited by density-dependence. It also assumes instantaneous conversion of prey into new predators, and does not include satiable predation, density-dependence, or social status among coyotes. The basic model is composed of two equations representing the change in the jackrabbit population, J, and the change in the coyote population, C,

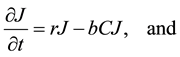(1)

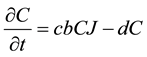, (2)

where r is the jackrabbit intrinsic growth rate per year and b is the attack rate of coyotes on jackrabbits per year. The parameter c represents jackrabbit conversion efficiency into new coyotes, measuring the relationship

between new coyotes and the number of prey required to support them. Lastly, coyotes die randomly every year at a constant rate, d. Jackrabbits reproduce at a rate proportional to the current abundance of jackrabbits, while they die of predation at a rate proportional to the abundance of coyotes. Coyote abundance increases simultaneously with the death of jackrabbits, and decreases at a constant rate across all seasons.

The Rosenzweig and MacArthur model incorporates density dependence among the jackrabbits with the addition of a carrying capacity parameter, K. In this model, the per-capita growth rate for jackrabbits would be density-dependent,

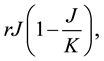
where 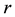is the intrinsic growth rate per year. The model also includes type II functional response by Holling (1959) for saturable coyote predation,

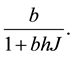
Handling time (in years) per prey item and the capture rate per year are included in the parameters 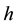and 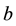respectively, describing how time spent interacting with prey dominates a predator’s time budget when prey are encountered frequently. The Rosenzweig and MacArthur model, including all of these mechanisms, is written

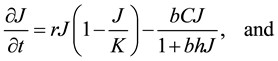(3)

(4)

where and 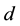are again the yearly prey conversion and coyote death rates.

Additionally, the coyote death rate parameter, 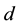, was allowed to change at a (to be determined) time, ,

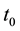to allow variable death rates in response to changes in coyote bounties and harvest rates that occurred during the course of data collection.

2.2.2. Discrete Models

Discrete models reflect seasonal differences occurring in survivorship parameters such as increased mortality in winter. Additionally, it is assumed that reproduction primarily occurs in the spring and thus new individuals are added to the population once annually. Since populations depend only on states in the previous season, seasonality effects are strict and immediate. The Beverton-Holt model was modified to include factors associated with the existence of a hierarchal social structure among the coyotes by specifying a baseline number of territorial coyote pack members, g, which were assumed to always be present. This reflects a division of the Curlew Valley landscape into pack territories. The number of coyotes supported in territories is assumed to be constant, since coyote packs typically cooperate to obtain resources in their own territory and are therefore less sensitive to the fluctuating abundance of jackrabbits.

However, not all coyotes live in packs; young coyotes in particular may become “transient” as pups mature and begin to forage on their own. These transient coyotes, T, were assumed to be most responsive to fluctuations in prey abundance with survivorship of pups dependent on the abundance of jackrabbits during the winter of gestation. Resource availability when coyote pups are born would influence both litter size and pup survival. Hence, jackrabbit abundance when pups are born is likely to affect coyote abundance two years later (Figure 2).

We assumed the transient population, , is a function of surviving transients from last year, plus new transients comprised of surviving pups which were dependent on the abundance of jackrabbits from two years ago. This seems counter-intuitive, since pups mature in a year or less. However, we assume that pup survival is most strongly influenced by jackrabbit abundance during the winter/spring of gestation (, letting the index denote fall of year). The year in which pups would be able to forage on their own and become transient would be the year after their birth year, thus adding to the transient population in year. The predator

conversion rate is denoted by c, and the annual survivorship of the transients is denoted by. The total number of coyotes observed should consist of both transients and alpha pack members. The effects of satiation among coyotes is included with the parameters b and a, reflecting the maximum predation rate and half-saturation constant, respectively.

Jackrabbits in this model were assumed to follow a Beverton-Holt nonlinear response with intrinsic growth rate and carrying capacity,

(5)

(6)

(7)

The predation and satiation rates are denoted by b and a respectively. This model includes both the effects of social status (i.e. a constant number of territorial coyotes and fluctuating abundance of transients) and satiable predation among coyotes, as well as density-dependent growth for the jackrabbits.

The preceding models were parameterized using only fall indices, but the data set included some years with spring data as well. To take advantage of this, we split the discrete model biannually to test for seasonal differences in survivorship and hopefully to gain leverage on the parameters. Jackrabbits in the spring, , were assumed to be directly proportional to the surviving jackrabbits from the winter, excluding the possibility of winter births. Winter predation from coyotes was not explicitly considered since we found some evidence of prey- switching during this time. Jackrabbits in the fall followed the same function as in the previous model, with density dependence and satiable predation included, giving

(8)

(9)

where denotes winter jackrabbit survivorship, and characterize carrying capacity and growth as described above, and satiation and predation are reflected in the parameters and. Jackrabbits in the spring consisted of the surviving jackrabbits from the fall, where jackrabbits in the fall included new jackrabbits born in the spring.

Social structure among the coyotes was reflected by a constant number of territorial coyote pack members, , and variable numbers of transient coyotes not associated with packs,. To preserve model structure for comparison with the un-split model, however, we maintained the assumption that the effects of jackrabbit abundance on pup production is lagged an entire year, giving

(10)

(11)

where is winter survivorship, is the prey conversion rate, and the parameters and again correspond to predation and satiation. The total number of coyotes, , consisted of the transient coyotes plus the pack coyotes (Figure 3).

This model assumes that mortality primarily occurs in the winter, and new coyote pups are added to the population specifically in the spring since coyotes typically have only one litter of pups per year [19] . In addition, a time lag in prey conversion to new predators was included, with new transients dependent on the abundance of jackrabbits in the fall of the year before pup gestation. This time delay appears as a two-year lag: jackrabbits in the winter of gestation, , contribute to pup production for year and surviving pups contribute to in the spring, when new pups are born. Hence, the influencing factors of density-dependence, delayed predator response, satiable predation, social status, as well as seasonality, were included in this model.

These discrete models were also expanded to reflect possible changes in coyote management by allowing a change in the number of coyote pack members, g, taking place partway through the simulation. Other simulations were also tried which allowed for a change in the transient survivorship rate, f, to occur. This was done in an attempt to reflect how changing mortality might lead to the permanent increase in coyote abundance that started in the early eighties that could have resulted from changing coyote bounty prices.

2.3. Parameter Estimation and Model Comparison

Parameter estimates for the models were obtained using nonlinear MLE, assuming a Laplace distribution of errors, making it less sensitive to outliers than the normal distribution [20] . Additionally, the Laplace error model is appropriate for accommodating phase shifts between data and continuous models, which are exponentially distributed. The probability of observing coyotes and jackrabbits in year, given model predictions, and, is

where the error variances are for jackrabbits and for coyotes. Parameters were determined by minimizing the negative log-likelihood for all observations,

using in MATLAB.

Models were compared using Akaike Information Criterion, which measures goodness of fit based on the value obtained from the negative log likelihood function, , and the number of parameters in a model, [21] . An correction for small sample sizes, , includes an additional penalty for the number of samples,. Since our data consisted of just 31 points and could be considered small, we used to compare the different models. The equations for computing AIC values are

where small values indicate a good fit with the data. Consequently, increasing the number of parameters needing to be estimated for the model increases its value.

We also bootstrapped the data to produce histograms of distributions for all four general models: the “null” Lotka-Volterra model (1-2), the Rosenzweig and MacArthur model (3-4), and the two Beverton-Holt models which are differentiated by seasonality (5-7 and 8-11). We randomly eliminated three years from the data, with replacement, to ensure all models had the same number of observations (since some models included a two year time lag), and fit 1000 samples for each model. Vectors of values from converging MLE estimates for each model were then used to create the histograms for comparison. This produced a visual representation of goodness of fit for each model, and allowed for us to determine the probability that a model could outperform another model given the data.

3. Results

Both continuous and discrete models appeared to fit the data fairly well. In fact, the two models with the lowest values were the annual discrete Beverton-Holt model without seasonality, and the continuous Rosenzweig and MacArthur model (Table 1). Models that included density-dependence and satiable predation produced much better fits than the basic Lotka-Volterra model. The discrete Beverton-Holt models, split to account for spring/fall seasonality produced the largest AIC_c values, but this can partially be explained by the increase in the number of model coefficients.

The Lotka-Volterra model, our “null” model, turned out to give the least appealing visual fit to the data (Fig- ure 4). Problematically, coyote abundance remained about the same over the course of the simulation. The model correctly predicted the time of the third peak in jackrabbit abundance, but did not predict the second peak as a maximum (the peak in jackrabbit abundance around 1980 is higher than in 1970 and 1990) and over-predicted the first peak. However, it was not the worst fit of the models. The intrinsic growth rate of the jackrabbits was estimated to be 4.91/year and the capture rate, 0.753/coyote-year (Table 2). This was consistent with existing research on this species having high rates of both growth and mortality [11] . The prey conversion rate affecting the coyotes was estimated to be 0.0022 new coyotes/jackrabbit and their death rate 0.089/year.

This model did not correctly capture whatever influenced coyote fluctuations since abundances were predicted to be nearly constant over all years.

Adding a carrying capacity for the jackrabbits (although there is currently no direct evidence that jackrabbits are in any way resource-limited in Curlew Valley) and predator satiation for the coyotes greatly improved the fit in the Rosenzweig and MacArthur model, which had the second-lowest value. The first peak in jackrabbit abundance was clearly predicted accurately, and the other peaks were predicted quite close to the observed values as well (Figure 5). The jackrabbit growth rate, valued at 5.18/year, remained consistent with expectations (Table 3). The index value for carrying capacity was estimated to be approximately 251 individuals.

Predictions were again too stable for coyote abundance, producing only two minor maxima shortly after the rise in jackrabbit abundance in the early seventies and again in the early eighties. However, the prey conversion rate, estimated to be 0.014 new coyotes/jackrabbit, was more consistent with existing theory regarding energy transfer between trophic levels [22] . The coyote handling time per prey item and attack rate were estimated to be 78.3 minutes and 0.41/coyote-year, which both seem like realistic values. The coyote death rate also appeared reasonable at 0.13, suggesting approximately ten percent of coyotes die each year.

The same model was tried again allowing for a change to occur in the coyote death rate partway through the simulation to reflect a decrease in the coyote bounty that happened in the eighties. This produced a good visual fit to the data (Figure 6), but the addition of two new parameters (the new death rate and time of change) increased the AIC_c value to 523. Oddly enough, this significantly changed the parameter estimates for the jackrabbit growth rate (1.058) and their carrying capacity (605.23), but similar values were obtained for the satiation (170.55) and predation (29) rates. However, parameter estimates for the death rates were contrary to our expectations since the death rate increased slightly in 1974 from 0.54 to 0.62 whereas one would expect lower

mortality rates when bounties decreased (Table 4). Nonetheless, this model adequately predicted the oscillations of jackrabbit abundance and produces two distinct maxima in coyote abundance.

The Beverton-Holt model had the lowest AIC_c value (495) and included the effects of density-dependence, satiable predation, delayed predator response, and social structure among the coyotes. This discrete model predicted jackrabbit abundance fairly accurately, even capturing a higher abundance in 1980 than in any other year (Figure 7). The intrinsic growth rate for the jackrabbits was estimated to be 2.97/jackrabbit/year, and the carrying capacity 278.689 (Table 5). Satiation and predation rates were estimated to be 441.45 and 121.37, respec- tively. Transient survival, valued at 0.0763/year, was expectedly low. The number of coyote pack members was

approximately 0.12, and the prey conversion rate 0.0526/jackrabbit (recall that these parameter estimates reflect indices values, rather than actual population numbers). This was the only model in which the graph displayed three maxima of coyote abundance. However, the coyote population appeared to crash in 1990 when observed values were high.

Splitting the Beverton-Holt model by season failed to improve the fit. In fact, these models had the highest values (561.28 - 572.9), which were computed using only fall values for model comparison. Three distinct peaks in jackrabbit abundance were evident in both seasons, and coyote abundance seemed to be more accurately predicted by this model in the early nineties than in any other model (Figure 8). The jackrabbit growth

rate increased to 5.43/jackrabbit, and the carrying capacity remained about the same at 274.72 (Table 6). Both the predation and satiation rates were reduced by almost half because this model updates indices biannually instead of annually. Jackrabbit winter survival was estimated to be 0.67, and the prey conversion rate remained consistent at 0.104/jackrabbit. However, the number of coyote pack members in this model was estimated to be 3.21, significantly higher than the value obtained from the annual model. Coyote transient survivorship also changed considerably, increasing to 0.21.

This model was also adjusted, much like the Rosenzweig and MacArthur model, to allow for either a change in the number of coyote pack members, or for a change in the survivorship of transients to occur. This was done to account for changes that could have taken place in coyote harvest rates due to a decrease in the price of the coyote bounty. However, these adjustments produced unrealistic parameter estimates and neither simulation visually improved the fit.

Distributions of values for each model were computed by randomly eliminating three years from the data and fitting each model with the new data for 1000 different samples. values for converging solutions were then graphed with lines indicating the values for the original model fits consisting of all data years (Figure 9). These distributions depict the probability that one model could perform better than another. For example, the probability that seasonality would improve the Beverton-Holt model of the time series is. Similarly, it is shown that satiation and resource limitations are important factors affecting this system since both the Beverton-Holt model and the Rosenzweig and MacArthur model most probably outperform the Lotka-Vol- terra model.

4. Discussion

A variety of both continuous and discrete models competed to describe the details of a time series linking coyote and jackrabbit abundance indices in northern Utah/southern Idaho; the best models proved to be the simplest. The Lotka-Volterra model (1-2) was used as the null model and did not include any factors tested in the other models. Models which included the effects of density-dependence on jackrabbits and satiable predation performed better than the others. The model with the lowest value included the effects of social status and delayed predator response, suggesting these may be significant factors affecting this predator-prey system at the population level. The models that accounted for seasonal differences in critical parameters had much higher values, indicating that seasonality is not a significant factor affecting predator-prey oscillations.

The model with the lowest value, the basic Beverton-Holt model (5-7), included social status among coyotes and an effective carrying capacity of packs in Curlew Valley (i.e. a fixed number of territorial packs and a fluctuating number of transients). This supports the hypothesis that social structure could be a contributing factor to predator-prey dynamics in this system. Social status among canids may affect their response to fluctuating prey densities since coyote pack members are less likely to be prey-selective. Pack association allows coyotes to hunt collaboratively, giving them the ability to take down larger prey which could sustain the pack for a longer period of time than smaller prey. Thus, we can assume that a transient coyote’s diet mainly consists of small prey and in this case, almost exclusively black-tailed jackrabbits [11] .

Additionally, the basic Beverton-Holt model included a delayed predator response since incoming transients were dependent on the abundance of jackrabbits at the time of pup gestation (an index offset of two, reflecting dependence of pup survival on winter jackrabbit abundance during gestation, a year of maturation, and subsequent delay until effects of new transients are reflected in fall abundances). This is not a novel idea since predator abundance in these cyclical predator-prey systems often lags several years behind the prey species; Harrison (1995) included a delayed numerical response when modeling Luckinbill’s data. Thus, the inclusion of this type of time-lag of prey conversion into new predators could enhance other predator-prey models as well.

5. Conclusion

This paper illustrates how multiple, competing models can be used to evaluate the importance of possible mechanisms contributing to complex ecological interactions. Rather than trying to nest models, which intrinsically links some mechanisms to others, we constructed specific models for specific clusters of mechanisms. Models competed via model-independent information theoretic criteria, allowing us to discriminate among mechanisms, even using the non-reproducible time series for coyote-jackrabbit oscillations in the Curlew Valley. Similar approaches can help wildlife managers to evaluate population models and contributing mechanisms without as much need for difficult observations and manipulations, which would otherwise be required to reproduce long- term oscillations between predator and prey species.

Acknowledgements

We thank the Editor and the referee for their comments.

References