Open Journal of Genetics
Vol.07 No.01(2017), Article ID:74958,20 pages
10.4236/ojgen.2017.71003
Why Do We Care for Old Parents? Evolutionary Genetic Model of Elderly Caring
Takahiro Miyo
2-17-4 Misumi-cho, Higashimurayama-shi, Tokyo 189-0023, Japan

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 21, 2017; Accepted: March 26, 2017; Published: March 29, 2017
ABSTRACT
From the standpoint of evolution, caring for old parents may be maladaptive, because they have ceased reproduction, so that the benefit for inclusive fitness may not be expected. Then why do we care for old parents? In this study, the evolution of care for the elderly was examined, by using an evolutionary genetic model, in which pleiotropic constraints between behaviors expressed in different social contexts among family members were assumed. It was suggested that establishing a solid relationship with parents during infancy should be selectively favorable, even though old parents have to be cared for in the future, but that caring for old parents may be excluded from the population if this behavior imposes high costs on reproduction of the younger generation. Despite the diminishing numbers of individuals within the population, care for the elderly may not be readily selected against, but at the same time this may not contribute to the rate of increase in population size. The significance of discussing the behavior of elderly caring from the standpoint of evolutionary genetics was emphasized.
Keywords:
Elderly Caring, Evolutionary Genetic Model, Infancy, Pleiotropic Constraint

1. Introduction
Senescence, which is defined as the decline in a wide range of bodily functions with age, is an almost universal phenomenon among organisms [1] . In spite of its universality, the problem posed by this apparently deleterious phenomenon is to explain why organisms had evolved not to continue living and reproducing forever but to senesce and die ultimately. Evolutionary biologists have proposed solid theories to explain how senescence had been established and maintained by natural selection [1] . Among them, Medawar [2] [3] suggested the critical concept for solving this problem that the force of natural selection on deleterious genes declines with age. That is, as organisms age, they produce offspring, so that there would be essentially no effects of deleterious genes on fitness if these genes are expressed in fully late ages, because they have already produced enough offspring. Therefore, the later the deleterious genes are expressed, the weaker the force of natural selection. As a result, deleterious genes expressed late in life would not be eliminated from the population, and the population tends to accumulate these deleterious mutations, resulting in senescence and ultimate death of organisms as an inevitable consequence of evolutionary processes within the population.
While Medawar suggested the above evolutionary mechanism of senescence more than 50 years ago, he also raised the alarm about population aging in the last paragraph of the same paper, which is now a serious problem in such countries as Japan. He mentioned as follows:
“The moral is that the problem of doing something about old age becomes slowly but progressively more urgent. Something must be done, if it is not to be said that killing people painlessly at the age of seventy is, after all, a real kindness” (italicized by Medawar himself) [2] .
The above alarm statement by Medawar seems somewhat radical, but it is not a fantasy at all in such countries as Japan, where various problems resulting from population aging are and will be serious matters. In fact, at some nursing facilities for the elderly, it is not unusual that one sometimes hears old users saying “It is boring,” “I feel lonely,” “I want to die quickly,” and so on (the author’s care-worker experience).
The elderly over 65 years old in Japan are 33,920,000 people at the point of 2015, and the proportion of the elderly over 65 years old in the total population are 26.7% [4] . However, it is predicted that this proportion would keep rising from now on and reach 39.9% in 2060, which means one out of 2.5 people would be over 65 years old, while the whole Japanese population would keep decreasing. The number of elderly people who need nursing care is expected to increase rapidly, and in particular, it is predicted that patients over 65 years old suffering from dementia would reach about 7,000,000 people in 2025 (one out of 5 people over 65 years old) [4] . Despite the fact that not only elderly people but also old people requiring nursing care and dementia patients are increasing rapidly, there is the fear of serious lack of the care staffs in the future who should care for the elderly [5] . In addition, people in the state of so-called “double care”, who need to carry out caring for their old parents as well as their children simultaneously, reached more than 250,000 people, about 168,000 women and about 85,000 men [6] . If caring for elderly people is predicted to be a serious problem in Japan, would such a situation, in which elderly caring is cut off, be realized, as Medawar warned?
Care for offspring by parents itself is not altruistic, because the care would increase in their own fitness [7] ; however, caring for old parents by their offspring would be altruistic, because old parents should have ceased reproduction, so that it is unlikely that the care for the elderly would result in the benefit of fitness from the standpoint of inclusive fitness theory [8] . Because all psychological mechanisms causing costly altruistic behaviors should exist through population genetic processes, including natural selection [9] , if we care for old parents despite the fact that elderly caring costs very much, it is a kind of paradox in which not only proximate but also evolutionary mechanisms causing elderly caring need to be examined. In order to investigate the evolution of elderly caring, an approach using evolutionary genetic models was adopted, because evolution of a trait must be ultimately understood in terms of changes in gene frequency or its equivalent, even though it may be an invisible psychological trait [10] .
Most behaviors are widely believed to be multifactorial [11] , and many human psychological traits are influenced by genetic factors [12] . Like other complex human behaviors, elderly caring must also consist of many components, both physical and psychological, each of which must itself consist of many components, which may be influenced by genetic and environmental factors. For example, there would be little doubt that some psychological traits, including attachment, empathy, and altruism between parents and offspring, more or less contribute to and play roles in caring for old parents. These psychological traits have in fact been suggested to have significant genetic components, based on twin studies [13] [14] [15] [16] . Thus elderly caring can be regarded as a quantitative trait, which is influenced by genetic as well as environmental factors, and the evolution of elderly caring would rather be investigated by using evolutionary genetic models.
Since an individual plays a different role in his/her family (i.e., offspring, parent, grandparent, etc.) through his/her life course, social behaviors among family members would be desirable to be treated as an integrated and developmental process [17] . Based on considerations using the theoretical models and empirical data, Lynch [17] suggested that if the types of behaviors which are expressed at different social contexts are genetically correlated, there would be some constraints in social interactions which can evolve among family members, and that such genetic constraints in behaviors should be common in natural populations. We human beings establish attachment (strong affectional bonds which result in close proximity to particular others) with our parents since infancy, and the attachment with parents is likely to continue through the whole life, “from the cradle to the grave” [18] [19] . Because we cannot survive without care by others during infancy, a genetic bias for developing solid attachment with care-givers, mainly parents, would increase the survival probabilities of infants and therefore fitness of parents per se [20] . In addition, because the attachment is likely to influence the strategies of offspring for survival and reproduction in the physical and social environments [21] [22] , it should play important roles in our whole lives in the evolutionary and adaptive terms. It would be healthy that parents and children in the solid attachment relationships would reverse their roles with time, when parents are getting older or disabled [19] . Therefore, it is necessary to examine whether establishing the solid attachment relationships with parents during infancy, such that children have to care for old parents in the future, is selectively favorable, even though there would not be payoff in fitness in the elderly caring. Thus, in this study, an evolutionary genetic model was developed, assuming pleiotropic constraints between interactions in the care for infants by parents and interactions in the care for old parents by children. In addition, because elderly caring is inevitably related to age relationships between family members (e.g., parents and children, grandparents and parents, and so on), evolutionary genetic models should take into account the age-structure of the population. Therefore, following a theory of kin selection in age-structured populations [23] , the selective advantage of the parent-offspring interactions involving elderly caring and the consequence of diminishing population size on it, which such countries as Japan are now or will be faced with, were examined in order to respond to the alarm proposition by Medawar [2] . The approach by Charlesworth and Charnov [23] is to examine the condition that a rare allele A2, which affects behavior and whose effects are assumed to be expressed in the heterozygous state, can invade a random mating population, which is initially fixed with the other allele A1 [1] . In this study, two main questions were examined using simple numerical models for hypothetical populations: 1) whether a rare dominant allele causing high levels of care for old parents as well as infants (high care gene) can invade a population that is initially composed of an relatively indifferent genotype, whose net reproduction rate was set to be one, and 2) whether a rare dominant allele causing an indifferent phenotype (indifference gene) can invade a decreasing population that is initially composed of a genotype providing high levels of care for old parents as well as infants, which might be the very situation that the countries suffering from population aging and diminishing population size, such as Japan, is being faced with.
2. Methods
2.1. Vital Statistics for the Hypothetical Population
Vital statistics for the hypothetical population suffering from population aging and diminishing population size were created, using population statistics of Japan available on the official website of National Institute of Population and Social Security Research, Japan (http://www.ipss.go.jp/syoushika/tohkei/Popular/Popular2016.asp?chap=0). Population statistics used were numbers of Japanese females by 5-year age-group from 2001 to 2012, and age-specific fecundity data for females by 5-year age- group from 2001 to 2007, which were transformed into the age-specific survival rates (P(x)) and fecundities (m(x)) for 5-year time-intervals. For example, using numbers of females by 5-year age-group in 2001 and 2006, P(x) for the 5-year interval was calculated. m(x) was calculated by multiplying the age-specific fecundities for each year by five. Thus seven sets of P(x) and m(x) for 5-year intervals were created for these years. After averaged over the seven years, one set of basic vital statistics were obtained for the hypothetical populations in this study (the upper Figure 1).
It would be better to note that my intention is not to predict the precise fate of the Japanese population, but to discuss the evolution of elderly caring in such populations suffering from population aging and diminishing population size as the Japanese population. Therefore, although there were some discrepancies, including some P(x) values larger than one which may be due to immigration, figures taken from the above website were used without any correction, because these discrepancies were minor in effect and did not change my conclusion.
Figure 1. Basic vital statistics used in the evolutionary genetic model (upper) and a sche- matic diagram depicting interactions among family members (lower). P(0) is the probability that a female child born at some point during a 5-year interval will live to the end of the interval; P(1) is the probability that a female aged between 0 and 4 years will survive for 5 years, and so on. Likewise, m(4) is the number of daughters a female aged between 15 and 19 years is expected to bear during 5 years, and so on.
2.2. Effects of Age-Specific Changes on Fitness
In populations suffering from population aging and diminishing population size, such as Japan, consequences of positive or negative changes in individual vital statistics on population increase would be especially important. The relationships between changes in individual vital statistics and corresponding changes in population growth were determined, by using the intrinsic rate of increase (r) as a measure of population growth and conducting partial differentiation of r with respect to P(x) or m(x) [1] [24] .
The relationship between these vital statistics and r, known as the Euler-Lotka equation, is
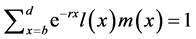 (1)
(1)
[25] , in which b and d represent a lower and an upper limit to the age of reproduction, respectively, and , the probability that a female survives from birth to age x. Applying implicit differentiation to Equation (1), the relationship between a change in lnP(x) and a corresponding change in r is obtained as follows
, the probability that a female survives from birth to age x. Applying implicit differentiation to Equation (1), the relationship between a change in lnP(x) and a corresponding change in r is obtained as follows
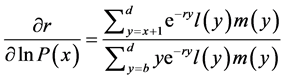 . (2)
. (2)
Likewise, the relationship between a change in m(x) and a corresponding change in r is
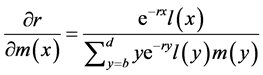 . (3)
. (3)
By obtaining these partial derivatives, we can find the effects of small changes in lnP(x) or m(x) on r [1] . Because r is a measure of population growth, here we can consider the impact of the changes in lnP(x) or m(x) on population increase and decrease.
For the basic vital statistics used in this study (the upper Figure 1), the intrinsic rate of increase, generation time, and net reproduction rate in the time-unit of 5 years were calculated by the Newton-Raphson iteration, using FORTRAN 77 program [26] . Then values of 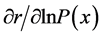 and
and 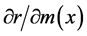 for each age were calculated using Equations (2) and (3).
for each age were calculated using Equations (2) and (3).
2.3. Evolutionary Genetic Model of Elderly Caring
Based on Charlesworth and Charnov [23] , whether or not a rare variant causing some behavioral trait can increase in frequency within a population fixed initially with the other variant was examined. Although the behavior of elderly caring is likely to be a complex quantitative trait, to which various factors, genetic as well as environmental, should contribute, it is necessary to incorporate the age-structure as an inevitable factor into a model, so that it would be too complex to deal with, if elderly caring is considered to be a quantitative trait. Therefore, the age-structure of the population is more emphasized, and a simple evolutionary genetic model, assuming two variants, one causing high levels of care for old parents as well as infants (high care gene) and the other causing relatively low levels of care (indifference gene), was adopted.
2.3.1. Invasion of a High Care Gene
It was assumed that a rare dominant autosomal allele causing high levels of care for the elderly as well as infants (A) was introduced into a random mating population fixed initially with a relatively indifferent allele (a), in which the initial frequency among individuals of age-class 4, starting reproduction, was set to be 1:100 (Aa:aa). Under this condition, combinations of mates and constitutions of family members were greatly simplified, so that the complex behavior of elderly caring could be examined more readily (Figure 2). It was assumed that there were genetic constraints between the types of behavior among family members in different social contexts, so that individuals possessing the dominant high care allele would establish a solid relationship between parents and offspring, in which parents would provide high levels of care for offspring, resulting in high survival rates during infancy, while offspring would provide high levels of care for old parents, resulting in high survival rates during old ages (the lower Figure 1). The genotype possessing the rare dominant allele should be Aa, and its mate should be aa, because individuals with two A alleles and mating between Aa individuals should be so rare that they could be ignored. Under these conditions, combinations of mates which should be taken into account were Aa × aa and aa × aa, and it would be expected that the former family would produce offspring whose genotype is Aa or aa (1:1), while the latter family would produce offspring whose genotype is only aa. Because one parent of the former family possesses Aa, offspring in this family would receive high levels of care during infancy; on the
Figure 2. A schematic diagram depicting how to calculate the total number of Aa newborns produced at time t (B2(t)), when a dominant A gene is rare. Here, c is the frequency of males among Aa newborns, l2(x) is the probability that an Aa female survives from birth to age x, and m2(x) is the number of female offspring which an Aa female of age x is expected to bear. 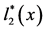 and
and 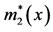 are the similar vital statistics for an Aa male. In this study, females and males were assumed to have the same vital statistics (for more details, see the text and [23] ).
are the similar vital statistics for an Aa male. In this study, females and males were assumed to have the same vital statistics (for more details, see the text and [23] ).
other hand, parents would receive high levels of care later in life because half the offspring are expected to possess Aa. Therefore, through parent-offspring interactions, Aa individuals were expected to have higher survival rates during infancy as well as later ages than aa individuals, at the level of individual genotypes. In this study, the basic P(x) calculated from the population statistics of Japan (the upper Figure 1) was used for P(x) of Aa individuals. For indifferent individuals, P(x) values during age-classes 0 - 2 (birth to 9 years old) and age- classes 15 - 17 (70 to 84 years old) were assumed to be 5%, 10% or 20% lower than those of the high care genotype. In addition, the actual P(x) values of Taiwan females in 1906, more than 100 years ago, were used for reference, which were calculated from the life table in [24] .
m(x) values were set to be those which made the net reproduction rate of the relatively indifferent genotype unity, by multiplying the basic m(x) values (the upper Figure 1) by constants. Under this condition, if the high care phenotype was selectively favorable, the relative frequency of the high care gene would be increased. If disadvantageous, its relative frequency would be decreased [1] . In addition, the state of so-called “double care” is likely to impose double burdens on people who care for old parents as well as children simultaneously [6] . Under these circumstances, care for old parents could impose much cost on offspring, and if there is no elderly caring, offspring could make an additional effort to reproduce. Thus negative effects of high levels of care for the elderly on reproduction were examined by assigning to the high care genotype the m(x) values which were reduced by multiplying constants. Under these conditions, female and male vital statistics were assumed to be the same for each genotype. After calculating the trajectories of the numbers of Aa and aa newborns (Figure 2), the relative frequencies of A allele (p2) were approximately estimated as 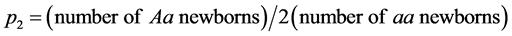 .
.
When the gene frequencies are sufficiently increased, these genes are not rare any more, so that a variety of combinations of genotypes among mates and among family members cannot be ignored. Under this situation, interactions between parents and offspring would be expected to be much more complex than the above situation. Whether or not the high care gene eventually reached fixation within the population was examined, using a discrete generation model, in which selection coefficients were determined based on the intrinsic rate of increase of the high care genotype [27] .
2.3.2. Invasion of an Indifferent Gene
It was assumed that a rare dominant autosomal allele causing a relatively indifferent behavior (B) was introduced into a random mating population fixed initially with a high care allele (b), in which the initial frequency among individuals of age-class 4, starting reproduction, was set to be 1:100 (Bb:bb). The procedure of the analysis was essentially the same as above, but here the factors of population aging and diminishing population size were taken into account, which Japan and other countries are now and will be faced with, so that the basic m(x) values calculated from the recent population statistics of Japan were used (the upper Figure 1). Therefore, it matters whether high care individuals prohibit indifferent individuals from increasing or relatively indifferent individuals increase in frequency and eventually exclude high care individuals, while the population size is decreasing. In addition, taking the cost of elderly caring on reproduction of offspring into account, negative effects of high levels of care for the elderly on reproduction were examined by assigning to the relatively indifferent genotype the m(x) values which were increased by multiplying constants.
2.4. Correlation in Survival Rate between the Immature and the Elderly
In this study, pleiotropic constraints in interactions affecting survival rates through life courses between parents and offspring were assumed. Because there is no research concerning the relationship between the level of care for infants and the level of care for old parents, to my knowledge, this assumption cannot be examined directly. However, if the pleiotropic constraints exist in interactions between parents and offspring, there should exist a positive correlation between survival rates during the immature stage and those later in life. Therefore, the correlation between survival rates in the immature ages and those later in life was examined. To do this, I used data from the 2015 revision of the World Population Prospects, obtained from the website of the United Nations (UN), Population Division [28] . The data I used included age-specific fertility rates, female population by 5-year age-group, and feminity ratio in age 0 - 1, for country- groups, classified by income levels, based on 2014 Gross National Income per capita from the World Bank, from 1990 to 2015. For each country-group (high-, upper-middle-, lower-middle-, and low-income), five sets of P(x) and m(x) for 5-year intervals were created from the data in the same way as the above hypothetical population. After age-classes were divided into three groups (0 - 14, 15 - 64, and 65+ years old), survival rates were averaged over the age-classes. The correlation coefficient in survival rate between age-group 0 - 14 and age-group 65+ was estimated. In addition, multiple regression analyses of survival rates of one age-group on survival rates of the other two age-groups were conducted, because each age-group should interact with other age-groups, so that survival rates of one age-group may be affected by those of the other age-groups.
Some P(x) values, especially for the high-income country-group, were more than unity, probably due to international migration. Although the net migration rates for these country-groups during the time period used in this study ranged from +3.7 to −1.3 per 1000 population per year [28] , any adjustment was not conducted for the population data from the UN, in order to avoid making arbitrary decision, so that survival rates at face value were used to obtain insights into the interactions affecting survival rates through life courses between parents and offspring.
3. Results
3.1. Effects of Age-Specific Changes on Population Growth
For the basic vital statistics of the hypothetical population used in this study (the upper Figure 1), which is suffering from population aging and diminishing population size, the intrinsic rate of increase, generation time, and net reproduction rate in the 5-year time-unit were estimated as −0.081, 6.56 (about 32.8 years), and 0.590, respectively.
The relationship between changes in lnP(x) or m(x) and corresponding changes in the intrinsic rate of increase (r) for the hypothetical basic population is shown in Figure 3. In the case of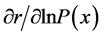 , the maximum value of 0.152 was attained in age-classes 0 to 3 (0 - 14 years old), but the value then decreased with age and reached zero in age-class 10 (45 - 49 years old). In the case of
, the maximum value of 0.152 was attained in age-classes 0 to 3 (0 - 14 years old), but the value then decreased with age and reached zero in age-class 10 (45 - 49 years old). In the case of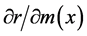 , the minimum value of 0.158 in age-class 1 (0 - 4 years old) increased gradually and reached the maximum value of 0.436 in age-class 16 (75 - 79 years old), and then decreased afterward.
, the minimum value of 0.158 in age-class 1 (0 - 4 years old) increased gradually and reached the maximum value of 0.436 in age-class 16 (75 - 79 years old), and then decreased afterward.
3.2. Invasion of a High Care Gene
The results of the evolutionary genetic analyses of elderly caring, in which a rare high care allele (A) was introduced into a population initially fixed with a relatively indifferent allele (a), are indicated in Figure 4(a). Within the population initially occupied by relatively indifferent individuals, whose survival rates during infancy and later in life were reduced by 5% to 20%, individuals possessing the rare high care allele increased in frequency, if they had the same m(x) as the indifferent. The larger the reductions in survival rate of indifferent individuals, the larger the rates of increase of the high care allele within the population.
However, the rates of increase in the frequencies of the high care allele were decreased, if high care for the elderly influenced reproduction negatively, and
Figure 3. The relationship between changes in lnP(x) or m(x) and corresponding changes in the intrinsic rate of increase, r.
Figure 4. Changes in frequency of a rare dominant autosomal allele which affects the behavior of carriers of the gene. ((a) (b)) The cases, in which a rare high care gene was introduced into a stationary population occupied by relatively indifferent individuals, whose survival rates during infancy and later in life were reduced by 5% to 20% and whose net reproduction rate was set to be one. (a) Age-specific fecundities were the same between the genotypes. (b) Age-specific fecundities for the high care genotype were reduced by 10% to 50% due to high levels of care for the elderly within the −20% indifferent population. ((c) (d)) The cases, in which a rare relatively indifferent gene causing 5% to 20% reduction in survival rates during infancy and later in life was introduced into a decreasing population occupied by high care individuals. (c) Age-specific fecundities were the same between the genotypes. (d) Age-specific fecundities for the −20% indifferent genotype were increased by 20% to 100% due to low levels of care for the elderly. The results using actual age-spe- cific survival rates for Taiwan females in 1906 are also shown in (a) and (c) for reference.
the high care allele was excluded from the population, if the negative effects on reproduction were sufficiently large. The changes in fecundity of the high care genotype, resulting in the intrinsic rates of increase equivalent to those of the relatively indifferent genotypes, are shown in Table 1. For example, the high care allele within the initial population fixed with the indifferent allele conferring −20% survival can increase in frequency, even though it brought about a 40% reduction in fecundity (the initial gene frequency of 0.0030 would indeed reach 0.0048 after 20 time-units (100 years); Figure 4(b)). However, it cannot, if m(x) was reduced by 50% (the initial gene frequency 0.0025 would indeed decrease to 0.0023 after 20 time-units).
Whether or not such rare alleles that increased initially within the population eventually reached fixation was verified, based on a discrete generation model. The results obtained by using the discrete generation model were consistent with those obtained by using the evolutionary genetic model taking into account the age-related interactions between family members, so that it was expected that the rare allele which increased initially within the population would increase until it reaches fixation (data not shown).
3.3. Invasion of an Indifferent Gene
The results of the cases where a rare relatively indifferent allele (B) was introduced into a decreasing population fixed with a high care allele (b) are shown in Figure 4(c). While the population was decreasing, the rare indifferent gene which reduced P(x) during infancy and later in life by 5% to 20% cannot increase in frequency within the high care population, if both genotypes possessed the same m(x).
In addition, the rates of decrease in the frequencies of the relatively indifferent allele were decreased, if low levels of care for the elderly had positive consequences on reproduction, and the indifferent allele would exclude the high care allele eventually from the population, if the positive consequences of low care on reproduction were sufficiently large. For example, the relatively indifferent allele which reduced P(x) during infancy and later in life by 20% could not increase in frequency even if m(x) increased by 1.8 times, but its frequency would finally
Table 1. The changes in fecundity of the invading genotypes which result in the intrinsic rates of increase equivalent to those of the initial populations.
aA rare dominant allele causing high levels of care for both offspring and old parents is assumed to be introduced into a stationary population fixed with an indifferent allele. bA rare dominant allele causing relative indifference is assumed to be introduced into a decreasing population fixed with a high care allele.
increase if m(x) increased by 2 times (Figure 4(d) and Table 1).
3.4. Correlation in Survival Rate between the Immature and the Elderly
There was a significant positive correlation in survival rate between the immature (0 - 14 years old) and the elderly (more than 65 years old) (Figure 5). The correlation coefficient was 0.930 (n = 20, P < 0.01) when survival rates of each year were treated separately, and 0.994 (n = 4, P < 0.01) when survival rates for each country-group were averaged over years. These survival rates also seemed to be associated with income levels from high to low.
Partial regression coefficients of age-group survival rate variables are shown in Table 2. The survival rate of the middle stage (15 - 64 years old) contributed
Figure 5. The correlation in survival rate between the immature (0 - 14 years old) and the elderly (more than 65 years old), estimated by using the population data for country-groups classified based on income levels [28] . Each black dot represents survival rates of each separate year for each country-group, and each larger circle represents survival rates averaged over years for each country-group.
Table 2. Partial regression coefficients of age-group survival rate variables.
*P < 0.05, ***P < 0.001. AGE1 represents the survival rate of the immature stage (0 - 14 years old), AGE2 the middle stage (15 - 64 years old), and AGE3 the elder stage (65+ years old).
significantly to the survival rates of both the immature and elder stages. On the other hand, the survival rate of the middle stage was significantly contributed by the survival rates of both the immature and elder stages. In the case of the survival rate of the elderly as a dependent variable, the intercept (−2.5625, P < 0.001) was remarkably negative, and a contribution to the survival rate from the middle stage (2.5962, P < 0.001) was remarkably large; on the other hand, the intercept (0.4658, P < 0.05) and a contribution to the survival rate from the middle stage (0.5089, P < 0.05) were significantly positive, when the survival rate of the immature stage was a dependent variable.
4. Discussion
The intrinsic rate of increase (r) and the net reproduction rate in the 5-year time-unit, estimated by using the basic vital statistics for the hypothetical population (the upper Figure 1), were −0.081 and 0.590, respectively. Because r needs to be more than zero and the net reproduction rate more than unity in order for the population to be maintained, this hypothetical population is considered a decreasing population, as expected. In general, the relationship between changes in m(x) and corresponding changes in r for an increasing population tends to decrease with age; however, it is possible that the relationship is not necessarily monotonic and could increase with age in the case of a decreasing population like this hypothetical population (Figure 3; [1] ). Under the conditions of population aging and diminishing population size, which countries such as Japan are or will be faced with, the relationship between changes in m(x) and corresponding changes in r increased with age, so that benefits contributed by old people to m(x) of younger individuals would have more positive effects on population increase than those contributed by any other young individual, if the amount of benefits is the same. At the same time, when elderly caring imposes costs on m(x) of younger individuals, it is suggested that costs by old people would have more negative effects on population increase than costs by any other young individual, if the amount of costs is the same. Therefore, if there are contributions from each age to young individuals, the positive contributions from older ages would be most efficient for population increase. On the contrary, it is suggested that decrease of the population such as Japan would get worse, if young individuals continue to receive costs of elderly caring.
In this study, the selective advantage of high levels of care for the elderly as well as infants was examined by using an evolutionary genetic model assuming two alleles, one causing high levels of care for old parents as well as infants and the other causing a relatively indifferent behavior. In the population fixed with the indifferent allele which reduces P(x) during infancy and later in life by 5 to 20%, the rare high care allele initially increased in frequency, if m(x) was the same between the genotypes (Figure 4(a)). Therefore, it is suggested that the establishment of a solid relationship with parents during infancy, which increases survival rates during that period, would be selectively favorable, even if it is necessary to take care of old parents in the future, from which benefits in inclusive fitness will not be expected. Because trajectories were below that for the Taiwan population in 1906, about 100 years ago (Figure 4(a), Taiwan), the assumption of 5% to 20% reduction in survival rates during infancy and later in life for relatively indifferent genotypes seems not to be unrealistic figures. However, the rates of increase in the frequencies of the high care allele were decreased, if high levels of elderly caring imposed costs on reproduction, and the high care allele was excluded from the population, if costs of care were sufficiently large (Figure 4(b) and Table 1). Therefore, it is suggested that high levels of care for the elderly as well as infants should not necessarily have absolute advantages, which may be excluded from a population if high levels of care for the elderly impose high costs on reproduction. However, in this situation, even though high levels of care for the elderly are matters of great concern, high levels of care for infants may also be excluded from the population due to pleiotropic constraints.
In addition, the case in which a rare relatively indifferent allele was introduced into a decreasing population fixed with a high care allele was examined, in order to discuss the possibility that we evolve to cut off caring for old parents, if elderly caring becomes a serious matter due to deterioration of population aging and diminishing population size, which is near the situation Japan is now or will be faced with. Although the population was decreasing, the rare relatively indifferent allele causing reduction in P(x) during infancy and later in life by 5% to 20% could not invade the high care population, if m(x) was the same between the genotypes (Figure 4(c)). Therefore, it is suggested that the genotype which establishes a solid relationship with parents and needs to take care of old parents altruistically in the future is still be selectively advantageous than the relatively indifferent genotype, even if the population does not have prospects for increase. As in the case of the high care gene invasion, the assumption of reduction in P(x) during infancy and later in life by 5% to 20% seems not to be unrealistic, because trajectories of the indifferent gene exclusion were above that for Taiwan population in 1906, which was rather near the trajectory for the case of 20% reduction (Figure 4(c), Taiwan). However, the rates of decrease in the frequencies of the relatively indifferent allele were decreased, if indifferent individuals performed low levels of care for old parents and increased reproductive efforts, and the indifferent allele would exclude the high care genotype eventually from the population, if low levels of care resulted in sufficient increases in reproduction (Figure 4(d) and Table 1). In this situation, however, the indifferent genotype was necessary to increase m(x) very much. For example, the indifferent genotype reducing P(x) during infancy and later in life by 20% needed to increase m(x) by about 100% in order to invade the population fixed with the high care allele. Therefore, selective advantages in establishing a solid relationship with parents are considered to be huge, even if old parents needs to be cared for altruistically in the future, which may impose even costs on reproduction. At the same time, the results that the indifferent allele was excluded from the population even though m(x) of the genotype was increased so much may indicate that the behavior of care for old parents would not be readily excluded from the population even though the population is decreasing, so that prohibiting population decrease would not be an easy task because this behavior would not be easily excluded from the population.
In this study, pleiotropic constraints in interactions between parents and offspring through the whole life were assumed in the evolutionary genetic model. In the analyses using the data from the UN [28] , the highly significant correlation in survival probability between the immature and the elderly was in fact estimated (Figure 5). Although survival rates would be affected by many factors, the assumption made in the model was supported at least superficially. On the other hand, the variation in survival rates seemed to also be related with income levels at the same time; the higher the income levels of country-groups, the higher the survival rates of both age-groups. Although any adjustment was not conducted in using the data from the UN [28] , this correlation is clear and seems reasonable from the standpoint of our expectations. Thus it is possible that the state of poverty or richness might affect the quality of the care for the young and the elderly; that is, environmental factors, such as poverty and richness, might influence the quality of the care. This may be true, but the question in this study in the first place is why we care for old parents, even though they have ceased reproduction and care for them costs very much. Therefore, the poverty-rich- ness hypothesis does not answer the question why we care for old parents under the wealthy condition, even though the gain of inclusive fitness should not be expected. If we care for the elderly under the wealthy condition, but cannot under the poor condition, it is likely that we have the nature to care for old parents, because it is rather natural that we cannot care for the elderly under the poor condition, even though we hope to care for them. Thus the results of this analysis might suggest the predisposed association between care for old parents and care for infants, supporting the assumption made in the evolutionary genetic model of the elderly caring.
The results of the multiple regression analyses indicate significant positive contributions from the middle age-group to the immature and the elder age- groups, and significant positive contributions from the immature and the elder age-groups to the middle (Table 2). Because survival rates among age-groups were also highly correlated with each other, caution should be taken, but the results did not necessarily indicate the same tendency among partial regression coefficients. Especially, when the survival rate of the elder age-group was a dependent variable, the contribution of the middle age-group was remarkably positive, and the intercept of the regression model when both independent variables were zero was remarkably negative, suggesting that survival rates in the elder stage may be largely dependent on the contributions from offspring generation, and that it may be difficult for the elderly to survive without their contribution. Therefore, the results of the multiple regression analyses may imply the existence of the care for the elderly. On the other hand, when the survival rate of the immature age-group was a dependent variable, the intercept of the regression model was significantly positive. Because infants cannot survive by themselves, the intercept, which should indicate the survival rate when contributions from the other age-groups are zero, may be expected to be near zero. Therefore, the significant positive intercept may imply the actual existence of contributions from a parental generation and a positive bias for survival of the immature stage when parental care is provided, which Bowl by [20] assumed. Overall, these results obtained by using population data from the UN [28] may be considered to support the assumption made in the evolutionary genetic model at least superficially.
5. Conclusions
From the standpoint of evolution, caring for old parents is considered to be a maladaptive behavior, because they have ceased to reproduce, so that this behavior is unlikely to produce benefits in inclusive fitness. In order for such a behavioral trait to be maintained within a population, some large benefits should exist in interactions between parents and offspring at other life stages. Thus in this study, I focused on the simple fact that we can survive only if someone (usually parents) does care for us, when we are infants, and discussed the evolutionary mechanism of elderly caring, using the evolutionary genetic model assuming pleiotropic constraints between care for infants by parents and care for old parents by offspring.
One of the most important consequences of population decrease, especially for human being, would be the increase of impacts from elder ages on population increase, and the ultimate population extinction would be the most important [1] . Therefore, deterioration of population aging and diminishing population size would result in serious social crisis. However, from the results obtained in this study, it may be concluded that the behavior of caring for old parents should not be excluded from a population until social situations are in serious crisis (establishing a solid relationship with parents and receiving care from them during infancy would have such a large selective advantage even if we have to care for old parents in the future), so that I believe it is unlikely that such a situation as in the Medawar’s alarming statement or the movie “The Ballad of Narayama” (directed by Keisuke Kinoshita, the theme of which is a Japanese folk tale of a poor farm village, in which old people who have reached 70 years old must be carried on their offspring’s shoulder to the mountain called Narayama and left there to die) will come about under current conditions. Nevertheless, this is not necessarily absolute, and it might be possible that the behavior of caring for old parents could be excluded from a population, if the serious social crisis comes about due to population aging and diminishing population size. However, the important point which should be emphasized is that behaviors which should evolve are not only abandonment of old parents but also abandonment of high levels of care for infants as well as positive interactions during other life stages, because elderly caring should be a behavioral trait which is not maintained within a population, if there are not pleiotropic constraints in interactions between parents and offspring. In other words, the behavior of elderly caring, which costs very much, should not be maintained within a population unless it entails high selective advantages during infancy and/or other life stages. Therefore, it is unlikely that abandonment of old parents will evolve in spite of the fact that people have received high levels of care from their parents in their childhood. When the serious social crisis in elderly caring has come about, it should be considered, not simply that it is better to abandon elderly caring, but that effects of abandonment of old parents may be brought about in various aspects of interactions between parents and offspring. In this sense, the following statement Medawar made is very suggestive:
“Those who argue that our concern is with the preservation of life in infancy and youth, so that pediatrics must forever take precedence of what people are beginning to call ‘gerontology’, fail to recognize that the outcome of pediatrics is to preserve the young for an old age that is grudged them. There is no sense in that sort of discrimination” (italicized by Medawar himself) [2] .
The world in which the elderly can be easily abandoned may also be the world in which lives of infants are in serious danger. In fact, among the Ache, ancestral hunter-gatherers living in Paraguay, South America, infanticides as well as geronticides were common [29] [30] . From the perspectives of people living at present, neither world would be happy. However, it is also true that abuses of children as well as the elderly are frequently reported in our society. Is it pessimistic to consider this situation as that the frequency of the relatively indifferent allele is increasing in our society?
My care-worker experience at nursing facilities for the elderly and the Medawar’s alarming statement quoted in Introduction motivated me to write this article and pose the serious matters of population aging and diminishing population size, which such countries as Japan are now or will be faced with. It is anticipated that the proportion of the elderly over 65 years old would reach about 40% of the total population in Japan in 2060, which is about 1.5 times as large as its current value [4] . It might be possible for us to imagine how serious this situation would be, if we consider a little about the situation, in which the number of old users in a nursing facility increases by 1.5 times under current care-work conditions. However, the real seriousness of the situation may not be imagined, because many events beyond our presumptions happen every day even at present. Although the evolutionary genetic model of elderly caring in this study is a simple numerical model for the hypothetical population suffering from population aging and diminishing population size, and there would be room for considering further details, such as the extent to which interactions between parents and offspring are pleiotropically constrained, I proposed the evolutionary mechanism of elderly caring in order to discuss this serious problem from various perspectives, other than social or political sciences. After discussing the evolutionary mechanisms of senescence, Medawar mentioned.
“¼ there was some truth amidst a good deal of what we can now see to be nonsense, and¼ it would stir up his successors to think up a more polished and cogent explanation” (italicized by Medawar himself) [3] .
I hope there is some truth in the model used in this study, which could result in valuable discussion and constructive criticisms for the future generations.
Acknowledgements
I thank Professor Brian Charlesworth (Univ. of Edinburgh) and Emeritus Professors Yuzuru Oguma (Univ. of Tsukuba) and Kenichi Aoki (Univ. of Tokyo) for valuable comments and suggestions on the manuscript. I am grateful to Dr. John Cartwright (Univ. of Chester) for his suggestions on this research at the early stage and to Mr. Takuji Miyo and Ms. Sachiko Miyo for valuable discussion on elderly caring. Finally, I would like to express my sincere appreciation to users and staffs at nursing facilities where I worked as a care-worker to provide me with invaluable opportunities for thinking about elderly caring.
Cite this paper
Miyo, T. (2017) Why Do We Care for Old Parents? Evolutionary Genetic Model of Elderly Caring. Open Journal of Genetics, 7, 20-39. https://doi.org/10.4236/ojgen.2017.71003
References
- 1. Charlesworth, B. (1994) Evolution in Age-Structured Populations. 2nd Edition, Cambridge University Press, Cambridge.
https://doi.org/10.1017/CBO9780511525711 - 2. Medawar, P.B. (1946) Old Age and Natural Death. Modern Quarterly, 1, 30-56. (Reprinted in Medawar, P.B. (1981) The Uniqueness of the Individual. 2nd Revised Edition, Dover, New York, 1-27)
- 3. Medawar, P.B. (1952) An Unsolved Problem of Biology. H. K. Lewis, London. (Reprinted in Medawar, P.B. (1981) The Uniqueness of the Individual. 2nd Revised Edition, Dover, New York, 28-54)
- 4. Cabinet Office, Government of Japan (2016) Annual Report on the Aging Society. (In Japanese)
http://www8.cao.go.jp/kourei/whitepaper/w-2016/gaiyou/28pdf_indexg.html - 5. Aoki, M. (2016) In Graying Japan, Caregivers in Short Supply. The Japan Times, 28 June, 3.
- 6. Otake, T. (2016) Burden of “Double Care” on the Rise. The Japan Times, 7 May, 3.
- 7. Charlesworth, B. (1978) Some Models of the Evolution of Altruistic Behaviour between Siblings. Journal of Theoretical Biology, 72, 297-319.
- 8. Hamilton, W.D. (1964) The Genetical Evolution of Social Behaviour. Journal of Theoretical Biology, 7, 1-16.
- 9. Wilson, D.S. (2015) Does Altruism Exist? Culture, Genes, and the Welfare of Others. Yale University Press, New Haven.
- 10. Aoki, K. (1984) A Quantitative Genetic Model of Two-Policy Games between Relatives. Journal of Theoretical Biology, 109, 111-126.
- 11. Crow, J.F. and Aoki, K. (1982) Group Selection for a Polygenic Behavioral Trait: A Differential Proliferation Model. Proceedings of the National Academy of Sciences of the United States of America, 79, 2628-2631.
https://doi.org/10.1073/pnas.79.8.2628 - 12. Bouchard, T.J. (2004) Genetic Influence on Human Psychological Traits: A Survey. Current Directions in Psychological Science, 13, 148-151.
https://doi.org/10.1111/j.0963-7214.2004.00295.x - 13. Davis, M.H., Luce, C. and Kraus, S.J. (1994) The Heritability of Characteristics Associated with Dispositional Empathy. Journal of Personality, 62, 369-391.
https://doi.org/10.1111/j.1467-6494.1994.tb00302.x - 14. Finkel, D., Wille, D.E. and Matheny, A.P. (1998) Preliminary Results from a Twin Study of Infant-Caregiver Attachment. Behavior Genetics, 28, 1-8.
https://doi.org/10.1023/A:1021448429653 - 15. Rushton, J.P., Fulker, D.W., Neale, M.C., Nias, D.K.B. and Eysenck, H.J. (1986) Altruism and Aggression: The Heritability of Individual Differences. Journal of Personality and Social Psychology, 50, 1192-1198.
https://doi.org/10.1037/0022-3514.50.6.1192 - 16. Zahn-Waxler, C., Robinson, J.L. and Emde, R.N. (1992) The Development of Empathy in Twins. Developmental Psychology, 28, 1038-1047.
https://doi.org/10.1037/0012-1649.28.6.1038 - 17. Lynch, M. (1987) Evolution of Intrafamilial Interactions. Proceedings of the National Academy of Sciences of the United States of America, 84, 8507-8511.
https://doi.org/10.1073/pnas.84.23.8507 - 18. Bowlby, J. (1977) The Making and Breaking of Affectional Bonds. I. Aetiology and Psychopathology in the Light of Attachment Theory. British Journal of Psychiatry, 130, 201-210.
https://doi.org/10.1192/bjp.130.3.201 - 19. Ainsworth, M.D.S. (1985) Attachments across the Life Span. Bulletin of the New York Academy of Medicine, 61, 792-812.
- 20. Bowlby, J. (1981) Psychoanalysis as a Natural Science. International Review of Psycho-Analysis, 8, 243-256.
https://doi.org/10.1111/j.1468-2273.1981.tb01318.x - 21. Chisholm, J.S. (1996) The Evolutionary Ecology of Attachment Organization. Human Nature, 7, 1-38.
- 22. Simpson, J.A. and Belsky, J. (2008) Attachment Theory within a Modern Evolutionary Flamework. In: Cassidy, J. and Shaver, P.R., Eds., Handbook of Attachment: Theory, Research, and Clinical Applications, 2nd Edition, Guilford Press, New York, 131-157.
- 23. Charlesworth, B. and Charnov, E.L. (1981) Kin Selection in Age-Structured Populations. Journal of Theoretical Biology, 88, 103-119.
- 24. Hamilton, W.D. (1966) The Moulding of Senescence by Natural Selection. Journal of Theoretical Biology, 12, 12-45.
- 25. Charlesworth, B. and Charlesworth, D. (2010) Elements of Evolutionary Genetics. Roberts and Company Publishers, Greenwood Village.
- 26. Miyo, T., Oguma, Y. and Charlesworth, B. (2003) The Comparison of Intrinsic Rates of Increase among Chromosome-Substituted Lines Resistant and Susceptible to Organophosphate Insecticides in Drosophila melanogaster. Genes and Genetic Systems, 78, 373-382.
https://doi.org/10.1266/ggs.78.373 - 27. Charlesworth, B. and Charlesworth, D. (1973) The Measurement of Fitness and Mutation Rate in Human Populations. Annals of Human Genetics, 37, 175-187.
https://doi.org/10.1111/j.1469-1809.1973.tb01825.x - 28. United Nations, Department of Economic and Social Affairs, Population Division (2015) World Population Prospects: The 2015 Revision.
https://esa.un.org/unpd/wpp/ - 29. Hill, K. and Hurtado, A.M. (1996) Ache Life History: The Ecology and Demography of a Foraging People. Aldine Transaction, New Brunswick.
- 30. Mace, R. (2000) Evolutionary Ecology of Human Life History. Animal Behaviour, 59, 1-10.







