Open Journal of Molecular and Integrative Physiology
Vol.2 No.1(2012), Article ID:17236,4 pages DOI:10.4236/ojmip.2012.21003
Use of fractal geometry to propose a new mechanism of airway-parenchymal interdependence
![]()
Respiratory Division, Department of Internal Medicine, Itami City Hospital, Hyogo, Japan
Email: in1007@poh.osaka-med.ac.jp
Received 11 October 2011; revised 25 November 2011; accepted 8 December 2011
Keywords: Self-Similarity of Bronchial Branching; Power Laws; Fractal Geometry; Airways-Parenchymal Interdependence
ABSTRACT
The topic of airway-parenchymal interdependence (API) is of great importance to those interested in identifying factors that influence airway patency. A carefully designed experiment has raised questions about the classical concept of API. This paper proposes a new mechanism of API. The pulmonary lobe is an aggregated body consisting of many Miller’s lobular polyhedrons and a fractal bronchial tree. The fractal cartilaginous bronchial tree was assumed to be characterized by both Horton’s ratio (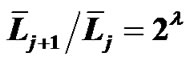 , where
, where ![]() and
and 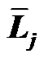 denote the mean lengths of branches at Horsfield’ order of j + 1 and j) and power laws between diameters and lengths of branches. Fluid dynamic parameters of fractal trees were assumed to be interrelated among powers and λ. A noncartilaginous lobular bronchiole is adjoined to the edge of a lobular polyhedron, and is encircled by an inextensible basement membrane to reflect a reversible relationship of rlLl = constant(c), where rl and Ll denote the diameter and the length of a lobular bronchiole, respectively. API at the level of the lobular bronchiole was described by
denote the mean lengths of branches at Horsfield’ order of j + 1 and j) and power laws between diameters and lengths of branches. Fluid dynamic parameters of fractal trees were assumed to be interrelated among powers and λ. A noncartilaginous lobular bronchiole is adjoined to the edge of a lobular polyhedron, and is encircled by an inextensible basement membrane to reflect a reversible relationship of rlLl = constant(c), where rl and Ll denote the diameter and the length of a lobular bronchiole, respectively. API at the level of the lobular bronchiole was described by 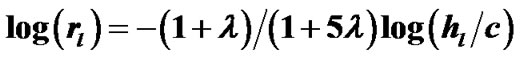 , where rl and hl denote the diameter of the lobular bronchiole and the parenchymal parameter relating the size of the lobular polyhedron, respectively. If the distribution in sizes of the lobular polyhedrons was described by a Weibull’s probability density function characterized by the shape parameter m as well as the fractal parameter λ = 0.5, the diameter R of a cartilaginous bronchial branch was determined by
, where rl and hl denote the diameter of the lobular bronchiole and the parenchymal parameter relating the size of the lobular polyhedron, respectively. If the distribution in sizes of the lobular polyhedrons was described by a Weibull’s probability density function characterized by the shape parameter m as well as the fractal parameter λ = 0.5, the diameter R of a cartilaginous bronchial branch was determined by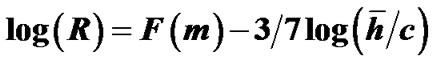 , where F(m) denotes a function of m, and
, where F(m) denotes a function of m, and ![]() denotes the mean size of the polyhedrons in the lobe. As a conclusion, API can be described by a combination of both lobular API and corresponding adaptive changes in the degree of contraction of airway smooth muscles.
denotes the mean size of the polyhedrons in the lobe. As a conclusion, API can be described by a combination of both lobular API and corresponding adaptive changes in the degree of contraction of airway smooth muscles.
1. INTRODUCTION
Excessive airway narrowing is a hallmark of asthma and chronic obstructive pulmonary disease (COPD) [1]. It results from maximal shortening of airway smooth muscle, leading to severe obstruction or even closure of the airways. In contrast, traction bronchiectasis has been recognized in high-resolution computed tomography (HR-CT) scanned images from patients with idiopathic pulmonary fibrosis (IPF) [2]. Parenchymal attachment to the adventitial wall of the airways in the lung is widely believed to contribute to the loads, measured in the airway smooth muscle, and, hence, it is assumed to be a significant factor in limiting airway narrowing and in producing traction bronchiectasis. Noble et al. [3], how ever, have raised questions about this common assumption. In a carefully designed experiment in mid-sized cartilaginous porcine bronchi, they found that the force pulling on the smooth muscle layer by the parenchyma surrounding the adventitial airway wall was insignificant and that it did not restrict luminal narrowing of the airway. The results suggest that parenchymal tethering may not play an important role in the altered airway caliber and smooth muscle function observed in COPD and IPF.
As Mandelbrot stated in his elegant monograph [4], biological branching systems, including the human bronchial tree, exhibit a fractal nature, i.e., a scale-independent self-similarity in the bifurcation pattern of their architecture. The fractal dimensions have been measured using various techniques. Fluid dynamic parameters of the bronchial tree as the conduit system are derived in power functions of radius including the fractal dimension in the exponents [5,6]. These fractal properties of the bronchial tree would be able to maintain the bronchial tree as the most effective passage for airflows [7].
The stiffer cartilaginous airways may have prevented parenchymal tethers from altering the adventitial diameter of the airways. Therefore, the increase in luminal diameter (traction bronchiectasis) in pulmonary fibrosis represents a relaxation uncoupling of the smooth muscle layer from the adventitia, and the decrease in luminal diameter in constricted airways represents a contraction uncoupling of airway smooth muscle layer. Due to their stiffness, the cartilaginous airways cannot change in length, but they can change in diameter. A more compliant non-cartilaginous airway, such as lobular bronchioles (less than 1 mm in diameter), would be more amenable to parenchymal pulling, to the extent that the elastic load can be transmitted to the smooth muscle layer without much hindrance. Thus, airway-parenchymal interdependence would exist at the level of the lobular bronchioles. In this study, we propose that airway smooth muscle can change the degree of its contraction to maintain the fractal geometrical properties of the bronchial tree. The resulting adaptive bronchoconstriction in COPD or adaptive bronchiectasis in IPF could occur through the airway-parenchymal interdependence at the level of the lobular bronchioles.
2. ASSUMPTIONS FOR MODELING
2.1. Fractal and Power Laws as Integration Rules of the Bronchial Tree
The pulmonary lobes are composed of many lobules (Miller’s secondary lobules), which are integrated into the whole lung by the bronchial tree. By applying the rules of integration to the bronchial tree, we assumed a power relationship between the diameters at a bifurcation (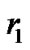 ,
,![]() and
and![]() ) in Figure 1, as follows:
) in Figure 1, as follows:
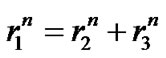 (1)
(1)
Biologists with an interest in the quantitative aspects of biological branching structures have found Horton’s branching law to be applicable to the bronchial tree [8].

Figure 1. Power laws between diameters at a bifurcation.
We implemented Horsfield’s version of Horton’s branching law as another assumption as follows:
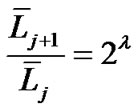 (constant) (2)
(constant) (2)
where  and
and 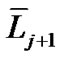 denote the mean length of a branch of Horsfield’s order j and j + 1, respectively, as shown in Figure 2.
denote the mean length of a branch of Horsfield’s order j and j + 1, respectively, as shown in Figure 2.
Flow travels through the diameter of larger parent branch (r1) connected to two smaller diameter daughter branches (r2 and r3) with flow adhering to a local powerlaw scaling relationship. The n is the junctional exponent. Data of bronchial or arterial trees were summarized by Suwa et al. and expressed by power of n = 2.7 [5,6,8].
In Horsfield’s ordering system, the first edge starts from the terminal, and when the edges of order j and order k come together at a vertex, the third edge is assigned to one order greater than the greater of j and k, or to j + 1 if j = k. The significance of Horton’s branching law is that it indicates a degree of topological self-similarity in the branching structure. Horsfield’s version of Horton’s law implies a geometrical self-similarity. Note that the symbol (-) means the average length of Horsfield’s order j or j + 1.
2.2. Fluid Dynamic Relationships between Fractal Dimensions
Fluid dynamic parameters of the bronchial tree as the conduit system are derived in power functions of the radius, including the fractal dimension in the exponents. Suwa and Takahashi [5] showed fluid dynamic relationships based on the fractal property in the length-radius relationship of various arterial branching (Eqs.3 and 4) as follows:
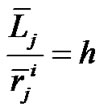 (constant) (3)
(constant) (3)
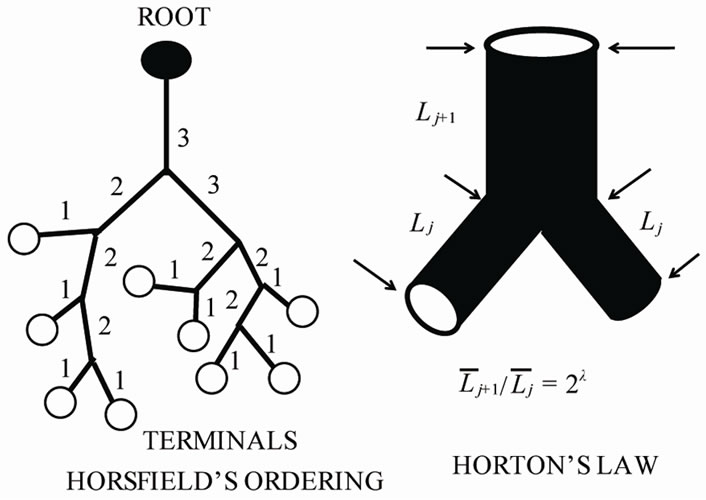
Figure 2. Horsfield’s ordering system and Horsfield’s version of Horton’s law.
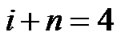 (4)
(4)
where 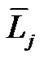 and
and ![]() denote the mean length and diameter of the bronchial branch of order j, respectively. We applied these additional assumptions for integration of pulmonary lobules to a whole lung.
denote the mean length and diameter of the bronchial branch of order j, respectively. We applied these additional assumptions for integration of pulmonary lobules to a whole lung.
2.3. Airway-Parenchymal Interdependence through the Lobular Bronchiole
The pulmonary lobe is composed of many bodies that consist of pulmonary parenchymal structures named lobular polyhedrons (Miller’s secondary lobules), each of which is supplied by a single bronchiole adjoined to an edge of a polyhedron (Figure 3). The bronchial tree is located in the adventitia that borders the lobular polyhedrons. Thus the airway-parenchymal interdependence would exist through interrelation between the lobular bronchiole and the corresponding lobular polyhedron. A non-cartilaginous lobular bronchiole is encircled by a non-elastic sheet structure of the basement membrane, which can change according to a reversal relationship between its diameter (rl) and its corresponding length (Ll) as follows:
 (constant) (5)
(constant) (5)
where c is the surface area of the basement membrane of the lobular bronchiole. If a lobule becomes larger, as a result of compliance with Eq.5, the corresponding lobular bronchiole becomes longer in length and smaller in di-
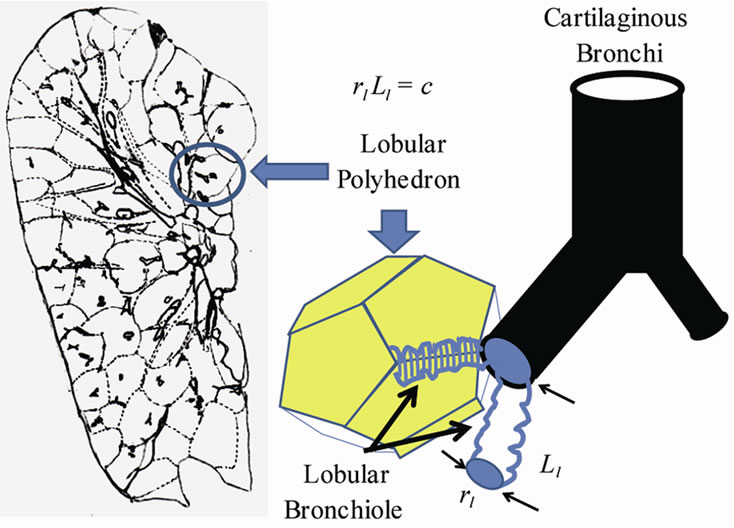 (a) (b)
(a) (b)
Figure 3. Lobular bronchiole/polyhedron interdependence. (a) Cross-sectional view of right upper lobe of human lung. Note that many lobular polyhedrons are aggregated in the lobe, and the bronchial tree is buried between the polyhedrons. (a) A non-cartilaginous lobular bronchiole is adjoined to the edge of a lobular polyhedron by adventitial connective tissue. The distortion of lobular bronchiole is limited by the basement membrane, a non-extensible membranous sheet of connective tissue, which is expressed by rlLl = constant(c), where rl and Ll are the diameter and the length of the lobular bronchiole, respectively.
ameter.
3. RESULTS
3.1. An Equation Describing Airway-Parenchymal Interdependence
In accordance with Eq.3, we introduced a parameter hl as the parenchymal parameter of the lobule relating to the size of the lobular polyhedron (Figure 3) as follows:
 (6)
(6)
Combining Eqs.5 and 6 produced Eq.7, which calculates the airway-parenchymal interdependence at the level of the lobular bronchiole as follows:
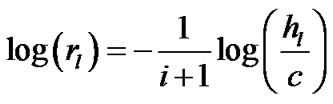 (7)
(7)
3.2. Relationship between Fractal Powers
The relationship between fractal powers can be examined using a set of symmetrical branching portions in the bronchial tree. Based on Eqs.1-3, these relationships were obtained as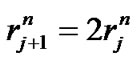 ,
, 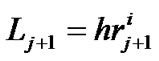 , and
, and ; then, by use of Eq.2 (Horton’s branching law), the relationship between powers i, n, and λ was derived as follows:
; then, by use of Eq.2 (Horton’s branching law), the relationship between powers i, n, and λ was derived as follows:
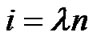 (8)
(8)
Thus, using Eqs.4 and 8, we obtained a set of equations describing the relationship between fractal powers as follows:
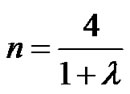 (9a)
(9a)
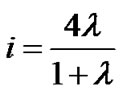 (9b)
(9b)
3.3. Lobar Airway-Parenchymal Interdependence
Combining Eqs.7 and 9b derived the expression of the airway-parenchymal interdependence in each lobule as follows:
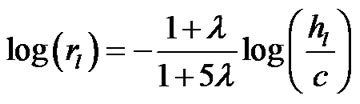 (10a)
(10a)
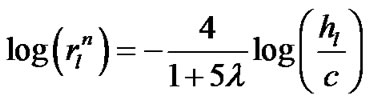 (10b)
(10b)
If a lobe was composed of a number N of lobular polyhedrons, the lobar bronchial diameter R was expressed according to Eq.1 as follows:
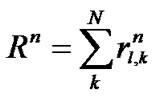 (11)
(11)
where 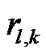 (
( ) denoted the diameter of each lobular bronchiole. Thus, by combining Eqs.10b and 11, we obtained an equation describing diameter R of the lobe consisting of lobules as a consequence of airwayparenchymal interdependence as follows:
) denoted the diameter of each lobular bronchiole. Thus, by combining Eqs.10b and 11, we obtained an equation describing diameter R of the lobe consisting of lobules as a consequence of airwayparenchymal interdependence as follows:
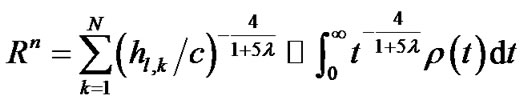 (12a)
(12a)
or
 (12b)
(12b)
where 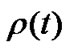 denoted a distribution function of parameter h in the lobe. To estimate the airway-parenchymal interdependence, it is necessary to measure the distribution function of the parenchymal parameters h. By measuring the length of the edges of the lobular polyhedrons seen on the surface of the upper lobe of human lungs, Min et al. [9] proposed a Weibull distribution function for describing the distribution in the size of lobular polyhedrons. If the distribution function of h was assumed to be equal to the distribution function in the size of lobular polyhedrons, ρ(t) was described by a probability density function as follows:
denoted a distribution function of parameter h in the lobe. To estimate the airway-parenchymal interdependence, it is necessary to measure the distribution function of the parenchymal parameters h. By measuring the length of the edges of the lobular polyhedrons seen on the surface of the upper lobe of human lungs, Min et al. [9] proposed a Weibull distribution function for describing the distribution in the size of lobular polyhedrons. If the distribution function of h was assumed to be equal to the distribution function in the size of lobular polyhedrons, ρ(t) was described by a probability density function as follows:
 (13)
(13)
where m > 0 was the shape parameter and η > 0 was the scale parameter of the distribution [10]. Thus, Eq.12b was transformed to Eq.14 by use of λ = 0.5 and 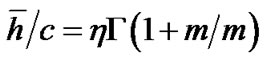 in Eq.13 as follows:
in Eq.13 as follows:
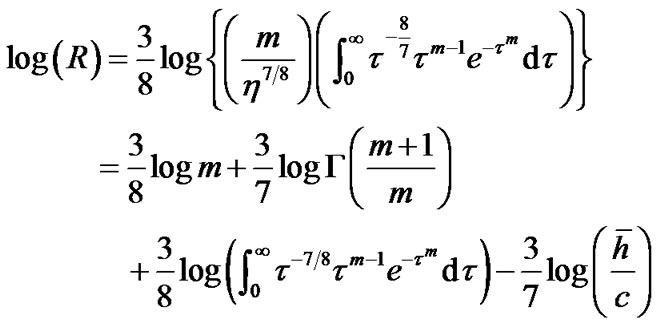 (14)
(14)
where  was the gamma function and
was the gamma function and ![]() was the mean value of lobular parenchymal parameter. Thus, the determinants of diameter R of the lobar bronchus were the shape parameter m and the mean of lobular parenchymal parameter
was the mean value of lobular parenchymal parameter. Thus, the determinants of diameter R of the lobar bronchus were the shape parameter m and the mean of lobular parenchymal parameter![]() as described by
as described by 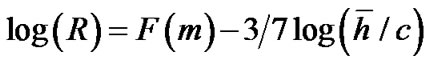 , where F(m) denotes the function of sum of the first three terms of Eq.14.
, where F(m) denotes the function of sum of the first three terms of Eq.14.
4. DISCUSSION
The degree of airway narrowing is determined largely by a balance between airway smooth muscle (ASM) contraction and opposing mechanical loads [1,2]. The afterloads that oppose airway narrowing consist of transmural pressure and elastic after-loads, which develop as narrowing progressively distorts tissue structures. These elastic after-loads arise both from within the airway wall and from surrounding lung parenchyma. Parenchymal attachment to the adventitial wall of airways has been widely believed to contribute to loads by ASM. Yet Noble et al. [3] have raised questions about this concept. They have shown that parenchymal elastic after-loads produced by distortion of lung parenchyma do not restrict airway narrowing in mid-sized cartilaginous bronchi. Therefore, the ASM layer of the cartilaginous bronchi would change itself between contraction and relaxation, uncoupled from parenchymal distortion. Thus, we aimed to show that another mechanism could explain the airway-parenchymal interdependence. The current study proposes a new mechanism of airway-parenchymal interdependence to explain bronchoconstriction in COPD and bronchiectasis in IPF.
Biologists with an interest in the quantitative aspects of biological branching structures, including bronchial trees, must perform laborious procedures to obtain good data and as a consequence, have implemented the properties of fractal (scale-independent self-similarity) geometry [4-7]. The most important step to describe the quantitative aspects of biological branching trees is to introduce ordering systems of classifying each branch of tree structure. In the long sequence of papers on lung airways by Horsfield et al. [12], the ordering method originally adopted is related to that proposed by Shreve [13], except that the edges of order j and order k come together at a vertex, and the third edge is assigned not to j + k but to one order greater than the greater of j and k, or to j + 1 if j = k. Horsfield’s ordering scheme is centripetal and topological and includes only edges. In this study, we adopted Horsfield’s ordering scheme as shown in Figure 2.
Horton drew attention to a number of empirical regularities, usually now known as Horton’s laws. The work of Horton [14] encouraged several investigators to find regularities corresponding to geometrical self-similarity or fractal properties such as Eq.2, which denotes geometrical self-similarity of the mean length of a branch. Several investigators, such as Horsfield and Cumming [15], Raabe et al. [16], and Horsfield and Thurlbeck [17], reported Horton’s ratio for the bronchial tree as ranging between 1.33 and 1.92, by which we calculated λ in Table 1. We used λ = 0.5 for the bronchial tree of humans. Since the diameter and length of the bronchial branch are determined largely by a balance between ASM contraction and opposing mechanical loads, the fractal properties of the bronchial tree would be maintained by active changes in the degree of contraction of ASM.
Concerning the study of Noble et al. [3], Seow [18] provided an editorial comment on the topic of airway

Table 1. The fractal parameter λ was calculated on the basis of Horton’s ratios, reported by Horsfield and collaborators. Note that λ values of bronchial trees are about 0.5 in humans.
parenchymal interdependence. He said that the topic of airway-parenchymal interdependence is of great importance to many of those who are interested in identifying factors that influence airway patency in health and disease. The first question is if a more compliant non-cartilaginous airway would be more amenable to parenchymal pulling, to the extent that the elastic load can be transmitted to the smooth muscle layer without much hindrance. The second question is how important, then, airway-parenchymal interdependence is in maintaining patency in small airways. The current study attempted to answer these questions raised by Soew, using the architectural relationship between a bronchial tree and an aggregate of lobular polyhedrons. Each lobular non-cartilaginous bronchiole is located on the edge of a corresponding lobular polyhedron with adventitial tissues (Figure 3). Lobular bronchiole/lobular polyhedron interdependence would operate at the level of the lobular bronchiole. The limitation against distortion of the lobular bronchiole is the inextensible sheet of basement membrane, which encircles the epithelial layer and creates a geometrical limitation, as expressed by Eq.5. Therefore, we have proposed that the lobular bronchiole/ lobular polyhedron interdependence is the basic phenomenon of so-called airway-parenchymal interdependence (Eq.7).
Each degree of airway-parenchymal interdependence at the level of the lobular bronchiole-polyhedron will be integrated into the whole lung through the fractal bronchial tree, as described by Eqs.12a and 12b. This integration has been expressed by Eq.14 when the distribution function of lobular parenchymal parameter is defined by the probability density function of Eq.13. Parameter h was introduced by Suwa and Takahashi [5] as the consequence of summarizing data of arterial trees in various organs. Parameter h relates to the size of the structural unit of the organ, such as the lobular polyhedron. Weibull’s distribution of Eq.13 is related to a number of other probability distributions. In particular, it interpolates between the exponential distribution (m = 1), the Rayleigh distribution (m = 2), and the normal distribution (m > 3) [10]. The unevenness in the size of lobules becomes particularly marked when shape parameter m is less than 3. Therefore, Eq.14 has revealed that the degree of constriction of the lobar bronchus will be dependent upon the unevenness in the size of the lobules and the average size of the lobular polyhedrons [11].
Magnetic resonance imaging (MRI) has developed as a research and diagnostic tool. MRI of inhaled hyperpolarized noble gases, mainly hyperpolarized helium-3 (3He), typically accomplished using a spin-exchange optical pumping method, provides nuclear polarization of up to five orders of magnitude compared with that achieved using thermal polarization [19]. This method provides ventilation images of the airways and airspaces of the entire lung, based on the lobular units with 1 mm in plane and 5 - 10 mm out of plane resolution within a breath-hold interval [20]. Diffusion-weighted MRI methods have been developed that are sensitive to 3He gas self-diffusion and provide a measure of the 3He signal that is dependent on the random Brownian motion of the 3He atoms. The MRI apparent diffusion coefficient (ADC) for 3He reflects the decreased diffusion of the 3He gas when inhaled and restricted by airways and airspaces in the lobule. The average displacement of helium is of the same order of magnitude as alveolar diameters (a few hundred micrometers) and, accordingly, the 3He ADC ranges from 0.8 cm2 per second for unrestricted free space to 0.66 cm2 per second for an elderly patient with COPD (FEV1 26% predicted) and 0.16 cm2 per second for a younger nonsmoker [21]. If 3He-ADC reflects the size of lobular polyhedron, it is possible to predict the distribution of hl as well as its mean ![]() in the lung by use of histograms of 3He MRI ADC in the lung.
in the lung by use of histograms of 3He MRI ADC in the lung.
In order to understand airway-parenchymal interdependence at the level of the lobular bronchiole polyhedron, it is necessary to determine what is operating as the mechanosensors of the bronchopulmonary system. To this end, studies on the neuroepithelial bodies, which are known to relate to mechanosensation of ASM and are widely distributed in the epithelium of the bronchial tree, are warranted. Brouns et al. [22] revealed the full complexity of NEB innervations, and at least some of the vagal afferent fibers connected to NEB were considered possible candidates as mechanosensors for integration into the bronchopulmonary system. We hope future studies will bring marked progress in this field.
We have shown, through the airway-parenchymal interdependence at the level of the lobular bronchiole polyhedron, that the diameter of a lobar cartilaginous bronchus will be determined by the average size of the lobular polyhedrons as well as by the distribution in size of the lobular polyhedrons. In conclusion, airway-parenchymal interdependence can be described by a combination of both lobular bronchiole/lobular polyhedron interdependence and the corresponding adaptive changes in the degree of contraction of airway smooth muscles in the cartilaginous fractal bronchi.
REFERENCES
- Macklem, P.T. (1998) The mechanism of breathing. American Journal of Respiratory and Critical Care Medicine, 157, S88-S94.
- Sumikawa, H., Johkoh, T., Colby, T.V., Ichikado, K., Suga, M., Taniguchi, H., Kondoh, Y., Ogura, T., Arakawa, H., Fujimoto, K., Inoue, A., Mihara, N., Honda, O., Tomiyama, N., Nakamura, H. and Müller, N.L. (2008) Computed tomography findings in pathological usual interstitial pneumonia: Relationship to survival. American Journal of Respiratory and Critical Care Medicine, 177, 433-439. doi:10.1164/rccm.200611-1696OC
- Noble, P.B., Sharma, P.K., McFawn, P.K. and Mitchell, H.W. (2005) Airway narrowing in porcine bronchi with and without lung parenchyma. The European Respiratory Journal, 26, 804-811.
- Mandelbrot, B.B. (1983) The Fractal Geometry of Nature. Freeman, New York. doi:10.1183/09031936.05.00065405
- Suwa, N. and Takahashi, T. (1971) Morphological and morphometrical analysis of circulation in hypertension and ischemic kidney. München.
- Kamiya, A. and Takahashi, T. (2007) Quantitative assessments of morphological and functional properties of biological trees based on their fractal nature. Journal of Applied Physiology, 102, 2315-2323. doi:10.1152/japplphysiol.00856.2006
- Weibel, E.R. (1991) Fractal geometry: A design principle for living oraganisms. American Journal of Physiology, 261, L361-L369.
- MacDonald, N. (1983) Trees and networks in biological models. Part III. Branching structures: Description, biophysics, and simulations. John Wiley & Sons Ltd., Chichester.
- Min, K., Kawai, M., Tamoto, A., Mozai, T. and Uchida, E. (1987) Geometrical analysis on the pulmonary lobular polyhedron (PLP) and consideration of the way of arrangement of PLPs in the lung. Japanese Journal of Thoracicic Diseases , 25, 722-730.
- Weibull, W. (1951) A statistical distribution function of wide applicability. Journal of Applied Mechanics, 18, 293-297.
- NIST/SEMATECH (2010) Weibull’s distribution, e-Handbook of statistical methods. http://www.itl.nist.gov/div898/handbook/eda/section3/eda3668.htm
- Horsfield, K., Dart, G., Olson, D.E., Filley, G.F. and Cumming, G. (1971) Models of the human bronchial tree. Journal of Applied Physiology, 31, 207-217.
- Shreve, R.L. (1966) Statistical law of stream numbers. Journal of Geology, 74, 17-37. doi:10.1086/627137
- Horton, R.E. (1945) Erosional development of streams and their drainage basins: Hydrophysical approach to quantitative morphology. Bulletin Geological Society of America, 56, 275-370. doi:10.1130/0016-7606(1945)56[275:EDOSAT]2.0.CO;2
- Horsfield, K. and Cumming, G. (1976) Morphology of the bronchial tree in the dog. Respiration Physiology, 26, 173-181. doi:10.1016/0034-5687(76)90095-5
- Raabe, O.G., Yeh, H.C., Schum, G.M. and Phalen, R.F. (1976) Tracheobronchial geometry: Human, dog, rat, hamster. Lovelace Foundation, Albuquerque.
- Horsfield, K. and Thurlbeck, A. (1981) Relation between diameter and flow in branches of bronchial the tree. Bulletin of Mathematical Biology, 43, 681-691.
- Seow, C.Y. (2005) Are you pulling my airway? European Respiratory Journal, 26, 759-761. doi:10.1183/09031936.05.00099905
- Saam, B.T. (1996) Magnetic resonance imaging with laser-polarized noble gases. Nature Medicine, 2, 358-359.
- De Lange, E.E., Mugler III, J.P., Brookeman, J.R., Knight-Scott, J., Truwit, J.D., Teates, C.D., Daniel, T.M., Bogorad, P.L. and Cates, G.D. (1999) Lung air spaces: MR imaging evaluation with hyperpolarized 3He gas. Radiology, 210, 851-857.
- Coxson, H.O., Mayo, J., Lam, S., Santyr, G., Parraga, G. and Sin, D.D. (2009) New and current clinical imaging techniques to study chronic obstructive pulmonary disease. American Journal of Respiratory Critical Care Medicine, 180, 588-597. doi:10.1164/rccm.200901-0159PP
- Brouns, I., Van Genechten, J., Hayashi, H., Gajda, M., Gomi, T., Burnstock, G., Timmermans, J.P. and Adriaensen, D. (2002) Dual sensory innervation of pulmonary neuroepithelial bodies. American Journal of Respiratory Cell Molecular, 28, 275-285. doi:10.1165/rcmb.2002-0117OC

