Open Journal of Molecular and Integrative Physiology
Vol.1 No.2(2011), Article ID:6950,6 pages DOI:10.4236/ojmip.2011.12004
Use of a mathematical model of autopoietic maintenance of pulmonary alveolar integrity to show a possible relationship between epithelial-mesenchymal transition and the genesis of emphysema and fibrosis
Department of Internal Medicine, Itami City Hospital, Hyogo, Japan.
Email: in1007@poh-osaka-med.ac.jp
Received 20 June 2011; revised 15 July 2011; accepted 1 August 2011.
Keywords: Autopoiesis; Pulmonary emphysema; Pulmonary fibrosis; Pulmonary stem/progenitor cells
ABSTRACT
Rationale: There is accumulating evidence that a group of stem/progenitor cells (SPCs) maintain alveolar epithelial integrity. Pulmonary emphysema is characterized by the histological finding of the loss of alveolar epithelial integrity along with corresponding bronchiolar fibrosis. Objectives: Based on the concept of autopoiesis (the capacity to produce oneself), we proposed a mathematical model in the maintenance of alveolar epithelial integrity as related to the genesis of pulmonary emphysema and fibrosis. Methods: A tessellation automaton model was used to describe the autopoietic dynamics of the bronchiolo-alveolar epithelial surface. The alveolar septal volume enclosed by the epithelial surface is a distributed system of discrete elements, which move by random walk in the manner of Brownian motion. Assuming that the numbers of components and events in the automaton are large, an approximate theoretical treatment in terms of differential equations is possible, allowing a set of partial differential equations to be produced. Results: 1) Assuming the loss of progenitor cells through the epithelial-mesenchymal transition (EMT), a sharp bifurcation between two qualitatively distinct regions of the phase space (one that is repaired completely, and another that has disappeared entirely) clearly appeared. 2) Thus, from the system of discrete and spatial partial differential equations, we obtained a system of ordinary differential equations in equilibrium conditions that defined a close relationship between the degree of emphysema, the density of alveolar septal fibroblasts, and the mean concentration of SPCs. Conclusions: A mathematical model of the autopoietic maintenance of the alveolar epithelial surface suggested a close relationship between alveolar emphysema and fibrosis and EMT in lungs affected by chronic obstructive pulmonary disease.
1. INTRODUCTION
The current enthusiasm for stem cell research derives from the hope that damaged or diseased tissues, including those affected by pulmonary emphysema, may be repaired through the manipulation of endogenous or exogenous stem cells [1]. Several putative adult epithelial stem cells have been identified in the mouse model system [2]. The response of the pulmonary system to injury revealed the potential of differentiated cells to act as stem or progenitor cells. A group of progenitor cells maintains alveolar epithelial integrity in the pulmonary parenchyma. However, the in vivo capabilities of these cells to contribute to different lineages and their control mechanisms remain unclear. The concept of autopoiesis conveys a sense of the capacity to produce oneself. Multicellular organs, including the lung, appear to be societies of cells under an autopoietic organization in which progenitor cells transform into different cell types and engage in maintaining a complex network of coordinated processes [3]. Bourgine and Stewart proposed a mathematical model of the minimum autopoietic system to characterize the autopoietic organization applicable to multicellular organs, including the lung. Using Bourgine and Stewart’s mathematical model, we obtained a set of equations to 1) describe the dynamic maintenance of pulmonary alveolar integrity in the parenchyma and 2) suggest that the ability of progenitor cells to differentiate into fibroblasts through the process of epithelial-mesenchymal transition (EMT) plays a critical role in the genesis of pulmonary emphysema and corresponding fibrosis.
2. METHOD OF MODELING
2.1. A Tessellation Automaton
A tessellation automaton, which is a discrete cellular automaton with purely local rules that specify computer simulations, can be used for the epithelial membrane (Figure 1). The epithelial membrane is formed of the epithelial C cells that are assembled to form a two-dimensional sheet. With a rate-constant kc per unit surface area, each epithelial C cell can disintegrate by apoptosis (C→C') and leave a hole in the epithelial membrane. Stem A cells circulating in the blood (the concentration of A is a1) diffuse freely into the septal space across the capillary endothelial sheet with an engrafting ratio (α). Within the septal space, the stem A cells diffuse freely. Two progenitor B cells are formed through transformation and proliferation of a stem A cell by a catalytic interaction with a fibroblastic F cell in the alveolar septal space (A + F→2B + F, with a rate-constant ka per unit concentration of the stem A cells). The epithelial membrane is impermeable to the progenitor B cells, which thus accumulate inside the alveolar septal space. The progenitor B cells also diffuse freely within the alveolar septal space. If a free progenitor B cell collides with the edge of a hole in the epithelial sheet, it integrates into the epithelial sheet and transforms to the epithelial C cell by a catalytic interaction with a neighboring epithelial C cell (B + C→C + C with a rate-constant kb per unit concentration of the progenitor B cells). If the hole becomes bigger, a free progenitor B cell does not always succeed in reconstructing the epithelial sheet, with the result that there is a finite probability that a progenitor B cell will transform into a fibroblastic F cell through EMT. Assuming that the numbers of components and events in the automaton are large, an approximate theoretical treatment in terms of differential equations is possible as follows.
2.2. Dynamics of Total Number of Epithelial Cells
The total quantity cM(t) of the epithelial C cells is considered in the epithelial membrane (Figure 2). The cM(t) belongs to the interval [0, c1], and c1 is the maximal quantity of the epithelial C cells where there are no holes. The homeostatic dynamics of cM(t) is as follows:
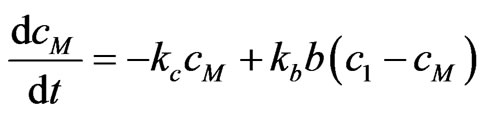 (1a)
(1a)
The first term represents the constitution of holes by apoptosis of the epithelial C cells C→C'. The second term represents the reconstitution of the epithelial sheet by the transformation of the progenitor B cells into the epithelial C cells B→C, because the probability of an encounter of the progenitor B cell with the epithelial C cell is proportional both to the concentration b of the progenitor B cells in the septal space, and to c1 - cM, the concentration of holes. The encounter between a free progenitor B cell and a hole in the epithelial sheet always succeeds in reconstructing the epithelial sheet when there is no loss of the progenitor cells through EMT. We refer to this as Model 1. If the holes become bigger and the progenitor B cells decrease in number in the septal space through EMT, the dynamics of the total number of the epithelial C cells can be modeled by modifying Equation 1a as follows:
 (1b)
(1b)
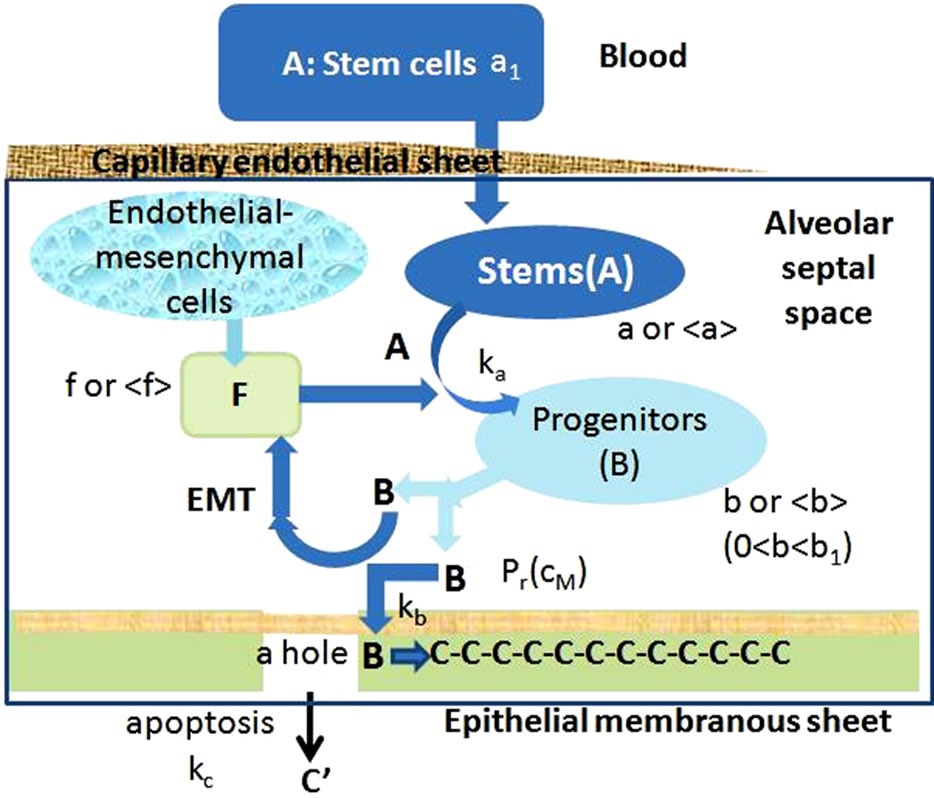
Figure 1. A schematic model of the dynamic maintenance of an alveolar epithelial sheet, based on recent accumulating evidence.
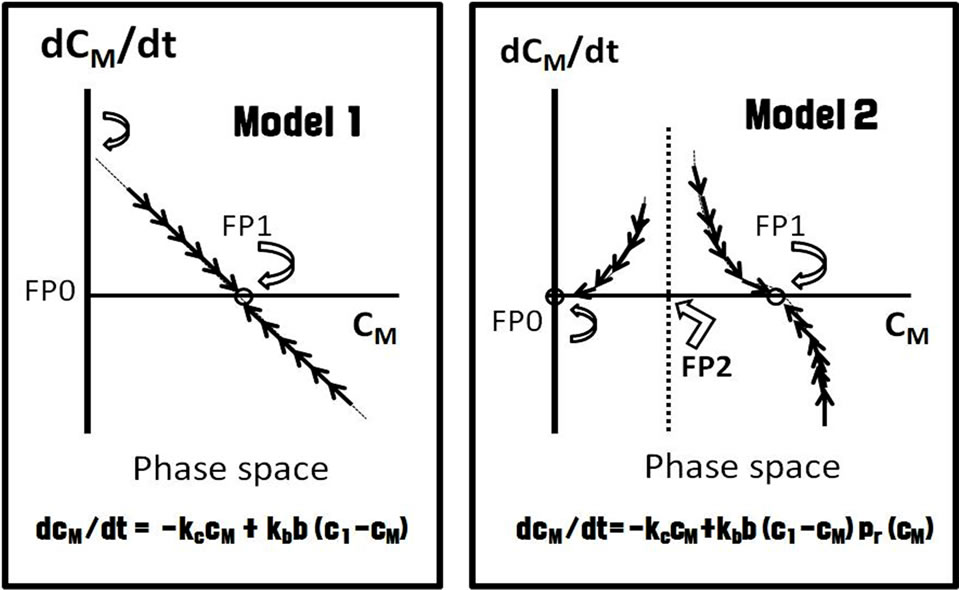
Figure 2. Phase trajectories of dynamics in Models 1 and 2.
where Pr(cM) is the probability that a progenitor B cell that hits the region of a hole will attach to the edge of the hole (i.e., the epithelial sheet is partially repaired). We refer to this as Model 2.
2.3. Random Walk Model as an Autopoietic System
The alveolar septal volume enclosed by the epithelial membrane is a distributed system of discrete elements {A, B}, which move by random walk in the manner of Brownian motion. It is known that random-walk processes can be approximated by partial differential equations for the local concentration a(x, t) of A and b(x, t) of B, the latter belonging to [0, b1], where b1 is the maximal concentration of the progenitor cells in the alveolar septal space due to its structural limitation [3]:
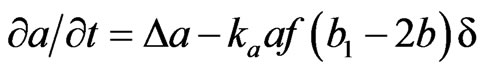 (2)
(2)
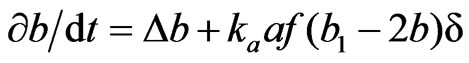 (3)
(3)
In these equations, the first term represents the diffusion due to random walk with Laplacian operator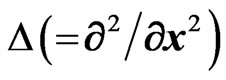 . The second term represents the transformation of A + F→2B + F (f is the local concentration of fibroblastic F cells in the alveolar septal space). The probability of this reaction is 1) proportional to a (the concentration of the A cells) in the alveolar septal space, 2) proportional to f (the local concentration of the F cells) corresponding to the encounter with a free F cell, and 3) proportional to (b1 – 2b) corresponding to saturation, because we suppose that there is an upper limit b1 to the possible concentration of the progenitor B cells.
. The second term represents the transformation of A + F→2B + F (f is the local concentration of fibroblastic F cells in the alveolar septal space). The probability of this reaction is 1) proportional to a (the concentration of the A cells) in the alveolar septal space, 2) proportional to f (the local concentration of the F cells) corresponding to the encounter with a free F cell, and 3) proportional to (b1 – 2b) corresponding to saturation, because we suppose that there is an upper limit b1 to the possible concentration of the progenitor B cells. 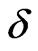 is a characteristic function for the alveolar septal space in the pulmonary parenchyma (
is a characteristic function for the alveolar septal space in the pulmonary parenchyma ( if but only if x is at an alveolar sheet, otherwise
if but only if x is at an alveolar sheet, otherwise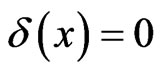 ).
).
2.4. Dynamics of Progenitor Cells in the Secondary Pulmonary Lobule
The secondary pulmonary lobule (SPL) is a fundamental unit of lung structure, and it reproduces the lung in miniature [4,5]. Each SPL has its own ventilation-perfusion environment. Thus, we considered the entire space of the automaton as the SPL. By integration of partial equations (2) and (3) over the space of the SPL, we obtained the macrodynamics of the total quantities of A and B over the total volume of the SPL, that is V< a > and V< b >, where < a > and < b > are the mean concentrations of a and b, and V is the total volume of the SPL. The integration of the Laplacian in Equation (2) gives the net flux of the stem A cells across the capillary endothelial sheet (the total surface area is S in the SPL) enclosing the alveolar septal space, α(a1 – < a >)S. The integration of the Laplacian in Equation (3) gives the net output flux of the progenitor B cells, kb< b >Σ(c1 − cM), which corresponds exactly to the creation of new epithelial cells in the entire space of the SPL. Thus we have
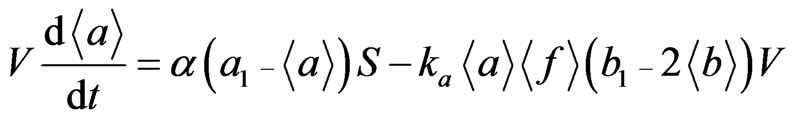 (4)
(4)
 (5)
(5)
where 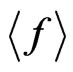 is the mean concentration of F cells in the alveolar septal space of the SPL.
is the mean concentration of F cells in the alveolar septal space of the SPL.
2.5. LAA% as the Indicator of Emphysematous Alteration of Alveoli
Several components of the SPL are normally visible on thin-section high-resolution computed tomography (HRCT) scans of the lung [4,5]. Emphysematous alterations of pulmonary parenchyma are also visible on HRCT scans as low-attenuation areas (LAAs) [5], and we can measure LAA% by the partial volume of LAAs in the total volume of the SPL (LAA% = ΣLAAs/V).
3. RESULTS
3.1. A Critical Value of Total Number of Epithelial Cells
In both Models 1 and 2, the key variable for understanding the structural dynamics of the system is c* = cM/c1, which is the proportion of the total surface area that is occupied by normal alveolar epithelial C cells. It should be noted that percolation analysis (a statistical analysis used to determine the movement and filtering of fluids through porous materials [6]) shows there is a critical value for c* (this value is dependent on the topological structure of the membrane, e.g., c* = 0.5 for a square lattice), below which the membrane no longer maintains topological continuity and fragments into two or more separate pieces. Thus, simultaneous depletion of more alveolar epithelial cells than c* due to injuries would induce emphysematous loss of alveolar surface in both models.
3.2. Repaired or Collapsed
When cM is more than the critical value c*, the dynamics of the system appears to have very different consequences for each of the two models. In order to characterize the qualitative behavior of two models mathematically, the procedure we proposed was to examine trajectories around the equilibrium conditions obtained by putting equations (1a) and (1b) to zero. Model 1 had a single fixed-point attractor (FP1) in the phase space, in which an encounter between a free B cell and a hole in the membrane would always succeed in reconstituting the membrane. In the case of Model 2, there were two separate fixed-point attractors, FP1 and FP0. FP1 in Model 2 was similar to FP1 in Model 1. At FP0, the system would be entirely collapsed and disappear. FP1 and FP0 were separated by a point of bifurcation (FP2), which was an unstable fixed point. Above PF2, the system would maintain itself dynamically with a basin of attraction FP1. That is, the rate of disintegration of membrane due to apoptosis C→C' would be balanced by the repair process B→C. Below PF2, the dynamics of repair would no longer manage to balance the formation of holes, and thus the dynamics of repair below the point of bifurcation no longer managed to balance the loss of alveolar epithelial cells. The emphysematous holes would increase in both size and number and would induce LAAs in the SPL.
3.3. Theoretical Relationship between Emphysema and Fibrosis
Assuming that a1 (the concentration of the stem A cells in the blood) was constant and the system was in equilibrium conditions, we obtained the equations to describe the degree of emphysematous loss of alveolar surface, expressed as LAA%, by putting the equations (4) and (5) on zero as follows:
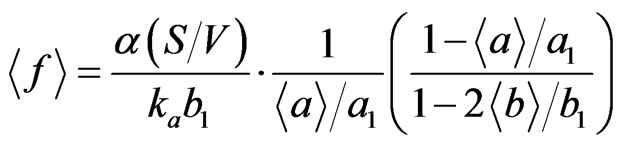 (6a)
(6a)
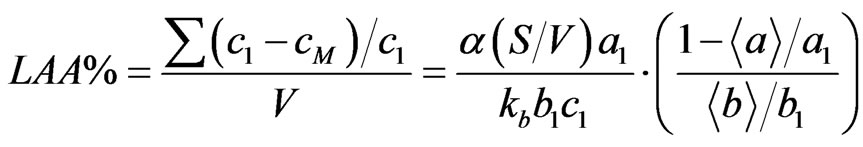 (6b)
(6b)
These equations have shown that the degree of emphysematous loss of parenchyma and the degree of alveolar septal fibrosis would be correlated with each other, and the correlations were shown graphically (Figure 3). The degree of emphysematous loss, expressed as LAA% was mainly dependent upon the mean concentration of progenitor B cells in the alveolar septal volume. The lower the concentration of stem A cells in the alveolar septal volume, the greater the density of septal fibroblasts, because the transition from stem A cells to progenitor B cells should be supported by interactions between stem A cells and fibroblasts.
4. DISCUSSION
Considerable excitement and hope have been generated by the possibility that exogenous stem/progenitor cells could be used to enhance lung repair or regeneration in patients with chronic obstructive pulmonary disease (COPD) [1]. During homeostasis, the adult stem cells rarely proliferate and are not predicted to undergo shape changes or to actively pattern the mesenchyme. There is no evidence that a multipotent stem cell population exists in the adult lung. By contrast, each region of the adult lung—upper and lower trachea, bronchi, bronchioles, terminal bronchioles, and alveoli—appears to be maintained by its own stem or progenitor cell population. Recently, one cell type that has received considerable attention is the dual-positive (Clara cell secretory protein positive [CCSP+] and surfactant protein C positive [SpC+]) cells located in the terminal bronchioles [7]. It has been suggested that these can contribute to both bronchiolar and alveolar lineages and may be the “true bronchiolo-alveolar stem cells (BASCs)” [8]. Dualpositive cells or BASCs would be the progenitor B cells we assumed in this study.

Figure 3. Graphical presentation of the relationship between parameters used to assess the degree of emphysema (Y axis) and the density of alveolar fibroblasts (X axis in the logarithmic scale).
The relevant adult marrow-derived cell populations capable of acquiring the lung phenotype have not been fully identified or characterized. Using parabiotic mice that share a common circulatory system, Abe and colleagues have shown that bone marrow-derived cells are recruited to the lung during elastase-induced emphysema [9]. The accumulating data suggest the existence of circulating stem A cells that we assumed and also raise the possibility of using of adult marrow-derived cells to treat COPD/emphysema [10,11]. Our understanding of the resident progenitor cellular components of the human lung is progressing rapidly, as is our understanding of the dynamic behavior of adult stem/progenitor cells. If future stem-cell-based therapies are to be successful, it is important that we fully understand that the basic regulating mechanism for the dynamic behavior of adult stem/ progenitor cells in the lung is a biosystem. The mathematical model we proposed in this paper is a first trial of establishing dynamical property of regulation system in the pulmonary parenchymal cells.
The concept of autopoiesis is attributed to Maturana and Varela, who specified a property common to all living organisms that is the necessary minimum for life [12]. Varela proposed a precise definition of an autopoietic system on the basis of three basic criteria in 2000: 1) it has a semipermeable boundary, 2) the boundary is produced from within the system, and 3) the boundary encompasses the processes that regenerate the components of the system [3,13]. Multicellular organs, including the lung, appear to be autopoietic societies of cells, differentiated into different cell types and engaged in a complex network of coordinated processes. If we consider the individual cells to be the components of the system, it is clear that a large number of these components disappear every day and are constantly renewed. Based on the theoretical approach of Bourgine and Stewart [3], we made the membranous epithelial system, consisting of pulmonary epithelial cells modeled as a distributed cellular automaton system, to control its own boundary conditions and to render possible the remodeling of the system as a random dynamical system. The key passage was the transformation from the system of discrete, spatial, partial differential equations (2) and (3) to the system of ordinary differential equations (4) and (5), where the sharp bifurcation between two qualitatively distinct regions of phase space clearly appeared (repaired completely at FP1 and disappeared entirely at FP0). This model has suggested that emphysematous alteration of pulmonary parenchyma is not abnormal but a result of dynamical process for maintenance of alveolar epithelial integrity as an autopoietic organization.
Emphysema is characterized by a pattern of alveolar destruction, resulting in marked airspace enlargement with a reduction in alveolar capillary exchange area or loss of parenchymal continuity of alveolar sheets. We are easily able to assess the emphysematous alterations of pulmonary parenchyma as the low-attenuation areas (LAAs) in HRCT scanned images [5]. The degree of emphysematous alterations can be assessed by determining the proportion of the pulmonary segments or the secondary pulmonary lobules occupied by LAAs. Our analysis of an autopoietic model of the dynamics of an alveolar epithelial system suggested a close relationship between the degree of emphysematous alterations and alveolar septal fibrosis through epithelial-mesenchymal transition (EMT). There is in vitro evidence of lung alveolar EMT, but it is still unknown if EMT occurs within the lung. Recently, Harada and colleagues reported that biopsies from fibrotic human lungs demonstrated epithelial cells with mesenchymal features that suggested EMT [13]. Thus, we suggest that biopsies from human emphysematous lungs would demonstrate the existence of EMT in the foci of bronchiolo-alveolar fibrosis, along with corresponding emphysematous alterations. Furthermore, as shown in Figure 1, alveolar fibrotic processes can occur in another vast network of cells, including fibroblasts, through EMT. Thus, alveolar fibrosis should be explained by another autopoietic model of alveolar endothelial, epithelial, and mesenchymal cell populations that maintain pulmonary parenchyma.
We suggested here the critical role of EMT in the genesis of emphysematous loss of pulmonary parenchyma and also revealed the possible correlations between emphysema and corresponding fibrosis by means of an autopoietic model of alveolar epithelial maintenance. We do not yet have evidence that supports these predicted results, which is why we need to conduct clinical and experimental investigations to help develop effective stem/progenitor cell therapies for chronic obstructive pulmonary disease.
Note that A, B, C, and F are stem cell populations, progenitor cell populations, functioning epithelial cell populations, and fibroblast populations, respectively. Fibroblastic cells come from both endothelial mesenchymal cell populations and progenitor B cell populations through the epithelial mesenchymal transition (EMT). See details in the Method of Modeling section of the text.
There is a single fixed-point attractor (FP1) in Model 1, described by the differential equation of dcM/dt = –kccM + kbb(c1 – cM). In the case of Model 2, described by the differential equation of dcM/dt = –kccM + kbb(c1 – cM)Pr(cM), there are two fixed attractors, FP1 and FP0, as well as an unstable point (a point of bifurcation), FP2. At FP0, the system has entirely collapsed and disappeared. Pr(cM) is the finite probability that a free progenitor B cell hits a hole, attaches on its edge, and is integrated into the epithelial sheet.
The parameters used to assess the degree of emphysema or the density of fibroblasts were calculated by (1 – < a >/a1)/< b >/b1 or by (1 – < a >/a1)/(1 – 2< b >/b1)/ < a >/a1, respectively. < a >/a1 × 100 = < a >% belongs to the interval [5, 95] or < b >/b1 × 100 = < b >% to the interval [5, 45], respectively. In equilibrium conditions, the degree of emphysema is determined mainly according to the concentration of progenitor cells in the alveolar septum. Since the septal fibroblasts have catalytic mechanisms that support the transition from stem cells to progenitor cells, a small number of stem A cells could produce enough progenitor B cells to maintain alveolar epithelial integrity in the septal space with more dense of fibroblasts.
REFERENCES
- Weiss, D.J., Jay, K., Kolls, J.K., Ortiz, L.A., et al. (2008) Stem cells and cell therapies in lung biology and lung diseases. Proceedings of the ATS, 5, 637-667.
- Herzog, E.L., Brody, A.R., Colby, T.V., et al. (2008) Knowns and unknowns of the alveolus. Proceedings of the ATS, 5, 778- 782.
- Bourgine, P. and Stewart, J. (2004) Autopoiesis and cognition. Artificial Life, 10, 327-345. doi:10.1162/1064546041255557
- Matsumoto, K. (1977) The lung. Tissues and organs II. In: Iijima, S., Irisawa, H. and Okada, T. Eds., Iwanami Series of Modern Biological Science, Tokyo, 315-372.
- Webb, W.R. (2006) Thin-section CT of the secondary pulmonary lobule: Anatomy and the image—The 2004 fleishner lecture. Radiology, 239, 322-338. doi:10.1148/radiol.2392041968
- Kesten, H. (2006) What is percolation? Notices of AMS, 53, 772-573.
- Kim, C.F.B., Jackson, E.J., Woolfenden, A.E., et al. (2005) Identification of bronchioalveolar stem cells in normal lung and lung cancer. Cell, 121, 823-835. doi:10.1016/j.cell.2005.03.032
- Kim, C.F. (2007) Paving the road for lung stem cell biology: Bronchioalveolar stem cells and other putative distal lung stem cells. American Journal of Physiology— Lung Cellular and Molecular Physiology, 293, L1092- L1098. doi:10.1152/ajplung.00015.2007
- Abe, S., Boyer, C., Liu, X., et al. (2004) Cells derived from the circulation contribute to the repair of lung injury. American Journal of Respiratory and Critical Care Medicine, 170, 1158-1163. doi:10.1164/rccm.200307-908OC
- Krause, D.S. (2008) Bone marrow-derived cells and stem cells in lung repair. Proceedings of the American Thoracic Society, 5, 323-327. doi:10.1513/pats.200712-169DR
- Wong, A.P., Keating, A., Lu, W.Y., et al. (2009) Identification of a bone marrow-derived epithelial-like population capable of repopulating injured mouse airway epithelium. Journal of Clinical Investigation, 119, 336-348.
- Varela, F. (2000). El fen’omeno de la vida. Ensayo, Santiago.
- Harada, T., Nabeshima, K., Hamasaki, M., et al. (2010) Epithelial-mesenchymal transition in human lungs with usual interstitial pneumonia: Quantitative immunohistochemistry. Pathology International, 60, 14-21. doi:10.1111/j.1440-1827.2009.02469.x

