Open Journal of Inorganic Chemistry
Vol.06 No.03(2016), Article ID:67968,8 pages
10.4236/ojic.2016.63013
Ellipsometric Study of SiOx Thin Films by Thermal Evaporation
David Salazar1, Roberto Soto-Molina1, Eder German Lizarraga-Medina1, Marco Antonio Felix2, Nicola Radnev2, Heriberto Márquez1
1Departamento de Óptica, CICESE, Ensenada, México
2Instituto de Ingeniería, Universidad Autónoma de Baja California, Mexicali, México

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 April 2016; accepted 2 July 2016; published 5 July 2016
ABSTRACT
This paper presents a study of amorphous SiOx thin films by means of Variable Angle Spectroscopic Ellipsometry (VASE) technique. Tauc Lorentz, Lorentz and Cauchy models have been used to obtain physical thickness and complex refractive index (n and k) from experimental data. In order to obtain a wide range to x stoichiometry values, the films were prepared by vacuum thermal evaporation of SiO on glass substrates, under different and controlled deposition conditions.
Keywords:
Ellipsometry, Refraction Index, SiOx Thin Films

1. Introduction
SiOx thin films have an important role in new technologies i.e. gate dielectric, silicon based light emitters, third generation solar cells, and SOI optical waveguides [1] - [6] . The SiOx is a material that can be fabricated by different techniques, in particular varying deposition conditions as pressure and evaporation rate when using thermal evaporation, silicon suboxide films with variable stoichiometry (SiOx, 1 < x < 2) whose optical properties depend on x value can be obtained [7] - [10] . Structural properties of the silicon oxide films studied by IR absorption and Raman spectra [11] reported that the structure of the films depends significantly on preparation method. Spectroscopic Ellipsometry and Transmission Electron Microscopy were used to obtain the volume fraction, f, the pure Si phase in silicon oxide thin films [12] . Variable Angle Spectroscopic Ellipsometry (VASE) is a robust technique based on interaction between film and polarized light, which can be used to determine complex refraction index and thickness of SiOx films. In order to obtain SiOx thin film dispersion, it is necessary to consider the film properties (transparency, thickness, rugosity, etc.), and select an appropriate model of dielectric function as Lorentz, Tauc Lorentz and Cauchy models that deserves to be studied; due there are a few works related with SiOx thin film dispersion curves [13] [14] . In this paper results on dispersion of SiOx thin films growth with different evaporation rates at different work pressure, obtained by means of VASE technique are presented.
2. Dielectric Function Models
Ellipsometry is an effective method to determine thin film thicknesses and their optical properties. These properties are not directly measured by ellipsometry, but a modeling procedure is needed to extract them from the measured ellipsometric spectra. During the evaluation, the unknown dielectric functions (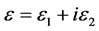 ) are usually modeled with oscillator function. The oscillator parameters are influenced by the composition and the structure of the material, since these microscopic properties determine the optical, and other physical properties of the film material. This section will explain various dielectric function models including the Lorentz, Cauchy, and Tauc-Lorentz models. Basically, all these models are derived from the Lorentz model [14] [15] .
) are usually modeled with oscillator function. The oscillator parameters are influenced by the composition and the structure of the material, since these microscopic properties determine the optical, and other physical properties of the film material. This section will explain various dielectric function models including the Lorentz, Cauchy, and Tauc-Lorentz models. Basically, all these models are derived from the Lorentz model [14] [15] .
2.1. Lorenz Model
A general and usual approach to fit the dielectric function is to use of Lorentz oscillators, this model assume that the dielectric permittivity can be described by a sum of multiple of resonance Lorentzian functions. This method is often used to have a smooth analytical representation of the dielectric function and is given by,
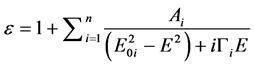 (1)
(1)
where E denote the photon energy, and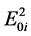 , Ai, Γi are the central photon energy, the amplitude, and the broadening of the ith oscillator, respectively. In Equation (1), the dielectric function is described as the sum of different oscillators [14] .
, Ai, Γi are the central photon energy, the amplitude, and the broadening of the ith oscillator, respectively. In Equation (1), the dielectric function is described as the sum of different oscillators [14] .
2.2. Cauchy Model
The Sellmeier model originated with the Lorentz model, expressed in terms of wavelengths, and replacing the plasma and resonant frequencies by empirical values. The Sellmeier model corresponds to a region where ε2 ~ 0 in the Lorentz model and this model can be derived by assuming Γ tends to zero at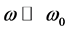 , where ω0 is resonant frequency of the electron. In this condition, if we transform dielectric constant using ω/c = 2π/λ, we obtain
, where ω0 is resonant frequency of the electron. In this condition, if we transform dielectric constant using ω/c = 2π/λ, we obtain
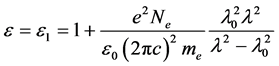 (2)
(2)
where me and e are the mass and charge of the electron, Ne is number of electrons per unit volume, c is speed of light in free space, ε0 is free space permittivity, ω is angular frequency and λ is wavelength of light.
On the other hand, Cauchy formula is a simplified version of the Sellmeier one, applicable to transparent material or spectral regions far from absorption lines; the Cauchy model is given by
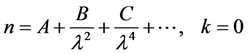 (3)
(3)
The above equation can be obtained from the series expansion of Equation (2). Cauchy model is an equation relative to the refractive index n, an approximate function of the Sellmeier model [14] .
2.3. Tauc-Lorentz Model
The Tauc-Lorentz oscillator is generally used for amorphous materials, for example for a-Si layers. The absorption band in the imaginary part of the dielectric function is defined as:
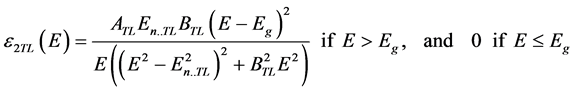 (4)
(4)
where ATL, En_TL and BTL, denotes the amplitude, position, broadening of the TL oscillator, respectively, and Eg is the band gap. The real part of the dielectric function is calculated using the Kramers-Kronig relation [15] .
3. Experimental
The SiOx thin films were prepared by means of thermal evaporation of silicon monoxide (Balzers SiO 99.5%), on transparent glass substrate, in a BOC Edwards Auto-500 thin film coating system. Spectral transmittance measurements of films were obtained with Stellar Net 2000 spectrophotometer and their ellipsometric characterization (thickness and refraction index measurements) was made by means of a J. A. Woollam M-2000 spectroscopic ellipsometer shown in Figure 1, with spectral range from 245 to 1000 nm, at incidence angles of 55˚, 65˚ and 75˚. It is known that SiOx films growth by thermal evaporation have an amorphous random network of tetrahedral coordinated silicon and oxygen and its stoichiometry is a function of the oxygen partial pressure and evaporation rate [10] .
In this work, SiOx thin films were deposited in a room temperature substrate (~30˚C), varying the evaporation rate and vacuum pressure of the chamber. A main goal is to modify films stoichiometry by different deposition rates, at two vacuum pressures: low vacuum ~10−4 Torr and high vacuum ~10−6 Torr. Table 1 shows evaporation parameters of the thin films, included thickness values obtained from quartz microbalance SQM Infinicom thin film deposition monitor. The source material SiO was evaporated from Tantalum boat using at a controlled deposition rate.
4. Results and Discussion
The fabrication conditions are expected to influence the optical properties of SiOx films, this section presents results of dispersion and transmission of SiOx thin films.
Figure 1. Main components of a variable angle spectroscopic ellipsometer (VASE).
Table 1. Evaporation parameters of SiOx films.
4.1. Transmission of SiOx Thin Films
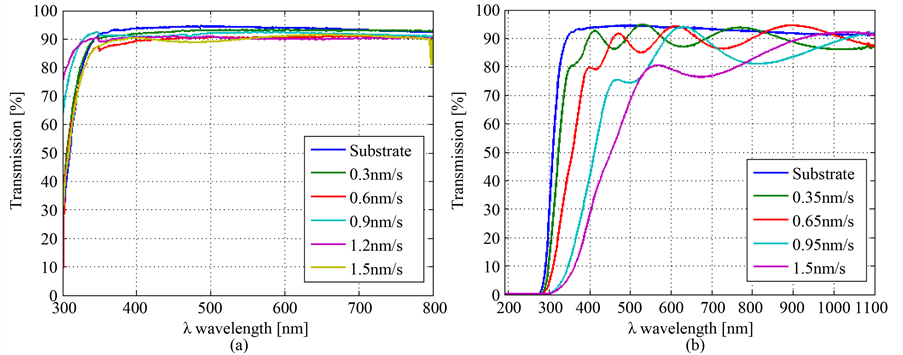
Figure 2 shows spectral transmittance of SiOx thin films fabricated a different evaporation rate, from 300 nm to 1100 nm range. Films obtained at low vacuum pressure have similar spectrums with a slightly decrease in transmission for higher evaporation rates, see Figure 2(a). On the other hand, spectral transmittance shown in Figure 2(b), obtained at high vacuum pressure, have the typical interference oscillations related to thin film thickness; from which more oscillations appears when increase film thickness [16] . Spectral transmission curves of SiOx films, presented in Figure 2, exhibit a transmission shift towards longer wavelengths; this shift can be associated to the amount of silicon (Si) in the film [8] . The spectral transmission of SiOx films, that had values of x close to 2, approaches to SiO2 spectrum, as expected. Otherwise when stoichiometry value of SiOx films is x close to 1, spectrum approaches to the SiO. Clearly, we can observe that when evaporation rate increase, transmittance curve have a shift towards higher wavelengths as consequence of more Si presence in SiOx films.
4.2. Ellipsometry of SiOx Thin Films
Here is considered that SiOx stoichiometry (1 < x < 2) can be tuned by means of evaporation rate of the film during the deposition process. The ellipsometry provides information of the refractive index dispersion curves and the physical thickness by means of polarization state changes described as the ratio (Ψ) between the amplitude reflection coefficients rp and rs and the difference between their phases (Δ). There are several models that use dispersion relations to obtain the thickness and the refractive index (real part n and imaginary part k). Normally, experimental data of Ψ and ∆ in spectral range are compared and adjusted with values of a particular model. Model parameters are adjusted to fit closely experimental and theoretical data. The fitting process includes a choice of initial values for the unknown parameters and the minimization of the function MSE (MSE mean squared error) by subsequent iterations [17] .
MSE function, which is essentially the sum of the squares of the differences between the measured and calculated data for each (∆, Ψ) pair, is given by
 (5)
(5)
where N is the number of measured Y and D pairs, M is the total number of variable parameters and σ is the standard deviations. The superscript Theo means theoretical model and the Exp means the experimental data. Nevertheless, obtaining a low MSE does not guarantee accurate thicknesses and optical constants.
Films that have a refractive index that varies with depth can be approximated as a set of layers, each one with an individual refraction index value. Furthermore, surface roughness can be taken account using the Bruggeman effective medium approximation (EMA) [18] . Physical interpretation of EMA theory involves small particles of one material suspended within a host material. Under this approximation, the optical constants can be mixed to satisfy
Figure 2. Spectral transmittance of SiOx film evaporated under: (a) low vacuum and (b) high vacuum.
electromagnetic equations: the Lorentz Lorenz equation for a mixture of material whose complex dielectric constants and volume fractions are ei and fi, and the Bruggeman formula for computing e in terms of ei and fi is,
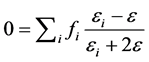 (6)
(6)
In this model, a single, planar layer, with thickness varying to provide the best approximation of the surface properties, can represent roughness.
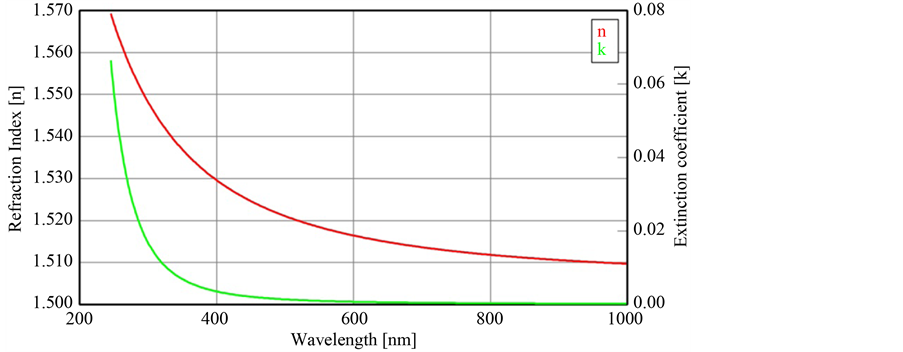
The ellipsometry software Complete EASE (J. A. Woollam Co., Inc.) was used to fit experimental and theoretical spectroscopy ellipsometry curves. With this software it is possible to select a physical model and fit with data acquired by means spectroscopic ellipsometry. A diffuse tape was used on substrate backside to eliminate or reduce secondary reflection, which can be a noise signal during measurements. Figure 3 shows dispersion curves obtained for substrate from 250 to 1000 nm with mean square error MSE of 1.88 and surface roughness of 2.7 nm.
During the fitting process, first SiOx samples were characterized by B-spline or Cauchy model, and with these initial values a second fitness process is realized using other models that have physical significance. In our work, Cauchy, Lorentz, and Tauc-Lorentz models were used due that are more appropriate to amorphous materials. Here, to obtain a better fit, a graded layer, with ten slices, was considered. Typical spectroscopic ellipsometry data for a SiOx film are shown in Figure 4. In this case, SiOx film was deposited at 0.35 nm/s and Figure 4(a) shows a fit with Cauchy model with values of MSE = 22.78, thickness 456.20 ± 0.48 nm and rugosity of 2.65 ± 0.13 nm and Figure 4(b) includes a gradient structure of the film with values MSE = 19.60, thickness 453.19 ± 0.43 nm and rugosity of 1.96 ± 0.12 nm. Figure 4(c) shows a fit for a SiOx film deposited at 0.35 nm/s using Lorentz model with MSE = 9.41, thickness 461 ± 0.23 nm and rugosity of 1.49 ± 0.06 nm and Figure 4(d) include a gradient structure of the film with MSE = 7.44, thickness 450.19 ± 0.54 nm and rugosity of 0.43 ± 0.07 nm.
Table 2 show results of calculated refractive indices for SiOx films using different models. Cauchy and Lorentz models were used to fit SiOx films obtained with low vacuum evaporation process, and Lorentz and Tauc- Lorentz models were used to fit SiOx films obtained with high vacuum evaporation process.
Figure 5 shows dispersion curves for SiOx films evaporated with different deposition conditions, presented in Table 1. From the last results, it is possible to note the influence of evaporation parameters on dispersion curves. In particular, SiOx films obtained at low vacuum condition have refractive index in the range of n ~ 1.4 - 1.53, and films obtained at high vacuum condition have higher values of refractive index i.e. n ~ 2.0. The evaporation rate has a notable influence on dispersion curves, and their contribution is described below. In general, we can observe little discrepancies on dispersion curves obtained from the different used models. B-spline model do not have a physical meaning and Cauchy Model is used on transparent films modeling. In order to obtain a best description of dispersion curves, a Lorentz model (oscillators) and Tauc-Lorentz (considering oscillators and density of states) models were used, including a refraction index gradient supposition.
Figure 3. Dispersion curves of glass substrate.
Figure 4. Fitted ellipsometric parameters Ψ and Δ of No. 6 sample using the Cauchy: (a) no gradient included, (b) gradient included; and Lorentz model: (c) no gradient included, (d) gradient included.
Table 2. Calculated refraction index for SiOx films obtained with different models at l = 633 nm.
Note*: Lv is Low vacuum, Hv is high vacuum, C is Cauchy model, L is Lorentz model, and T-L is Tauc-Lorentz model.
From dispersion curves shown in Figure 5 for SiOx films, it is possible to see a relationship between refractive index of the films and their evaporation rates; refraction index increase as evaporation rate increase. Previous works on the synthesis of SiOx films, have shown a direct relation between the stoichiometry x and the refractive index of the films [7] - [10] .
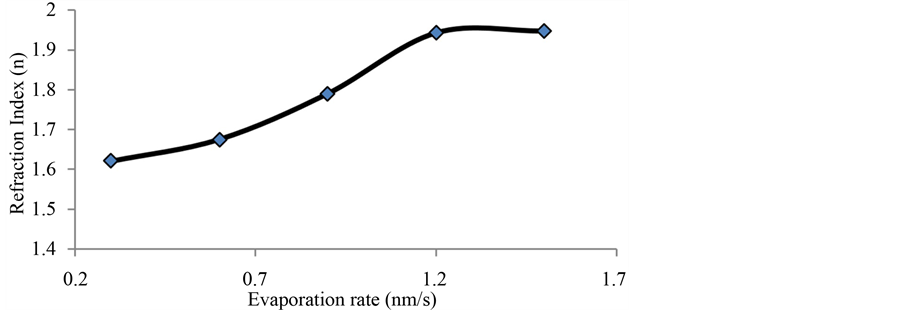
Figure 6 shows the refraction index of SiOx films at 633 nm as a function of evaporation rate, when deposited with high vacuum process of about ~10−6 Torr. Refractive index values of SiOx films have values in a range from 1.6 - 1.95; higher n values were obtained at higher evaporation rate, as is expected. At higher evaporation rates, the oxidation in the films is avoided and therefore approach to the stoichiometry and refractive index of
Figure 5. Dispersion curves obtained with VASE to films prepared by different deposition rate.
Figure 6. Refraction index (n) in function of evaporation rate at 10−6 Torr and l = 632.8 nm.
SiO films with x = 1. However, refractive index of SiOx films evaporated with low vacuum process of about ~10−4 Torr has lower values of n ~ 1.45 which is close to a SiO2 stoichiometry with x = 2. When the vacuum in the chamber is low, the film tends to oxide even for high evaporation rates. Furthermore, it can be appreciated that for higher evaporation rates (i.e. 1.5 nm/s) a higher refractive index is obtained, even at this vacuum. From the results presented it is possible to foresee the potential of modulation of refractive index of SiOx films as function of evaporation rate and vacuum pressure for application in integrated optical devices.
5. Conclusion
SiOx thin films have been obtained by thermal evaporation of SiO under low vacuum (~10−4 Torr) and high vacuum (~10−6 Torr) with different rates of evaporation from 0.35 to 2 nm/sec. Spectroscopic ellipsometry analysis of thin films was done by fitting experimental data of Y and D pairs with Lorentz, Tauc Lorentz and Cauchy models, showing little discrepancies and good agreement on dispersion curves obtained from the different used models. Dispersion curves of SiOx thin films indicate that it is possible to modulate refractive index of SiOx in a range of 1.42 to 1.95 at 633 nm as function of evaporation rate and vacuum pressure.
Acknowledgements
The authors would like to thank J. L. Angel-Valenzuela and J. Davalos for their technical support. R. Soto would like thanks to scholarship Grant CONACYT No. 369368.
Cite this paper
David Salazar,Roberto Soto-Molina,Eder German Lizarraga-Medina,Marco Antonio Felix,Nicola Radnev,Heriberto Márquez, (2016) Ellipsometric Study of SiOx Thin Films by Thermal Evaporation. Open Journal of Inorganic Chemistry,06,175-182. doi: 10.4236/ojic.2016.63013
References
- 1. Yao, J., Lin, J., Dai, Y., Ruan, G., Yan, Z., Li, L., Zhong, L., Natelson, D. and Tour, J.M. (2012) Highly Transparent Nonvolatile Resistive Memory Devices from Silicon Oxide and Graphene. Nature Communications, 3, Article ID: 1101.
http://dx.doi.org/10.1038/ncomms2110 - 2. Wang, G., Raji, A.R., Lee, J.H. and Tour, J.M. (2014) Conducting-Interlayer SiOx Memory Devices on Rigid and Flexible Substrates. ACS Nano, 8, 1410-1418.
http://dx.doi.org/10.1021/nn4052327 - 3. Kakiuchi, H., Ohmi, H., Yamada, T., Tamaki, S., Sakaguchi, T., Lin, W.C. and Yasutake, K. (2015) Characterization of Si and SiOx Films Deposited in Very High-Frequency Excited Atmospheric-Pressure Plasma and Their Application to Bottom-Gate Thin Film Transistors. Physica Status Solidia, 212, 1571-1577.
http://dx.doi.org/10.1002/pssa.201532328 - 4. Mazzarella, L., Kirner, S., Gabriel, O., Korte, L., Stannowski, B., Rech, B. and Schlatmann R. (2015) Nanocrystalline Silicon Oxide Emitters for Silicon Hetero Junction Solar Cells. Energy Procedia, 77, 304-310.
http://dx.doi.org/10.1016/j.egypro.2015.07.043 - 5. Littlejohns, C.G., Nedeljkovic, M., Mallinson, C.F., Watts, J.F., Mashanovich, G.Z., Graham T. Reed, G.T. and Gardes, F.Y. (2015) Next Generation Device Grade Silicon-Germanium on Insulator. Scientific Reports, 5, Article ID: 8288.
http://dx.doi.org/10.1038/srep08288 - 6. Subbaraman, H., Xu, X., Hosseini, A., Zhang, X., Zhang, Y., Kwong, D., Ray, T. and Chen, R.T. (2015) Recent Advances in Silicon-Based Passive and Active Optical Interconnects. Optics Express, 23, 2487-2511.
http://dx.doi.org/10.1364/OE.23.002487 - 7. Pivot, J. (1982) Mechanical Properties of SiOx Thin Films. Thin Solid Films, 89, 175-190.
http://dx.doi.org/10.1016/0040-6090(82)90446-1 - 8. Shabalov, A.L. and Feldman, M.S. (1983) Optical and Dielectric Properties of Thin SiOx Films of Variable Composition. Thin Solid Films, 110, 215-224.
http://dx.doi.org/10.1016/0040-6090(83)90239-0 - 9. Zuther, G., Hübner, K. and Rogmann, E. (1979) Dispersion of the Refractive Index and Chemical Composition of SiOx Films. Thin Solid Films, 61, 391-395.
http://dx.doi.org/10.1016/0040-6090(79)90485-1 - 10. Tomozeiu, N. (2011) Silicon Oxide (SiOx, 0 < x < 2): A Challenging Material for Optoelectronics. In: Predeep, P., Ed., Optoelectronics—Materials and Techniques, InTech, 56-98.
- 11. Nikitin, T. and Khriachtchev, L. (2015) Optical and Structural Properties of Si Nanocrystals in SiO2 Films. Nanomaterials, 5, 614-655.
http://dx.doi.org/10.3390/nano5020614 - 12. Mateos, D., Curiel, M.A., Nedev, N., Nesheva, D., Machorro, R., Manolov, E., Abundiz, N., Arias, A., Contreras, O., Valdez, B., Raymond, O. and Siqueiros, J.M. (2013) TEM and Spectroscopic Ellipsometry Studies of Multilayer Gate Dielectrics Containing Crystalline and Amorphous Si Nanoclusters. Physica E, 51, 111-114.
http://dx.doi.org/10.1016/j.physe.2012.11.015 - 13. Tauc, J. (1969) Optical Properties and Electronic Structure of Amorphous Semiconductors. In: Nudelmre, S. and Mitra S.S., Eds., Optical Properties of Solids, Springer, New York, 123-136.
http://dx.doi.org/10.1007/978-1-4757-1123-3_5 - 14. Fujiwara, H. (2008) Spectroscopic Ellipsometry: Principles and Applications. Wiley, England.
- 15. Budai, J., Hanyecz, I., Szilágyi, E. and Tóth, Z. (2011) Ellipsometric Study of SixC Films: Analysis of Tauc-Lorentz and Gaussian Oscillator Models. Thin Solid Films, 2985-2988.
http://dx.doi.org/10.1016/j.tsf.2010.12.073 - 16. Macleod, H.A. (2001) Thin-Film Optical Filters. CRC Press, London.
http://dx.doi.org/10.1201/9781420033236 - 17. Woollam, J.A., Snyder, P.G. and Rost, M.C. (1988) Variable Angle Spectroscopic Ellipsometry: A Non-Destructive Characterization Technique for Ultrathin and Multilayer Materials. Thin Solid Films, 166, 317-323.
http://dx.doi.org/10.1016/0040-6090(88)90393-8 - 18. Bosch, S., Ferré-Borrull, J., Leinfellner, N. and Canillas A. (2000) Effective Dielectric Function of Mixtures of Three or More Materials: A Numerical Procedure for Computations. Surface Science, 453, 9-17.
http://dx.doi.org/10.1016/S0039-6028(00)00354-X